等角度重采样在航空发动机振动分析中的应用*

陈 钊，杨现萍，冯巧宁

(中国飞行试验研究院发动机所，陕西西安 710089)

0 引言

航空发动机在工作中存在稳态与非稳态两种状态，当发动机处于稳态时，采用短时傅立叶方法即可对发动机振动数据进行分析，但是如果发动机处于过渡态，发动机转速随时间快速发生变化，此时采用短时傅立叶对发动机振动数据进行分析会存在很多问题，如果分析数据段选择过长，该时间段内发动机转速已经不是均匀转速，直接导致分析结果错误，如果分析时间过短，则傅立叶分辨率过低，计算结果不准确。针对以上问题，本文提出采用等角度重采样方法对航空发动机过渡态振动数据进行分析。

1 等角度采样方法介绍

考虑到旋转机械振动信号是以转角位置为自变量的周期平稳信号，人们提出了等角度采样方法，以及将非平稳的时域采样信号变成角域里周期平稳的信号。严格意义上的等角度采样是按照旋转部件所转过的等角度间隔进行采样，这需要安装有等角度间隔的光电编码器。现常见的等角度采样方法有3种，即硬件方法、软件方法和峰值搜索法［1-5］。笔者采用软件方法实现等角度重采样。计算阶次跟踪法的步骤如下［6］:

(1)对原始振动信号和转速信号分两路同时进行等时间间隔时域采样，得到异步采样信号。

(2)确定每个周期T的采样点数。

(3)根据步骤(2)确定的采样点数，对振动信号进行插值，求出其对应的幅值实现重采样，并生成振动信号的同步采样信号，即角域平稳信号。

(4)对重采样的信号进行快速傅里叶变换(FFT)，得到振动信号的阶次谱。

2 等角度采样法的仿真计算

航空发动机起动或停车过程中，航空发动机的转速会从0增加到100%或者从100%降低到0，现产生一组仿真数据，该数据振动幅值为1，转速从200 Hz线性变化降低到0。采用该数据来模仿发动机停车。

2．1 采用短时傅立叶方法处理仿真数据

对于过渡态的振动数据，比较传统的做法是采用短时傅立叶的方法处理过渡态振动数据，采用短时傅立叶的方法处理仿真数据如图1～3所示。

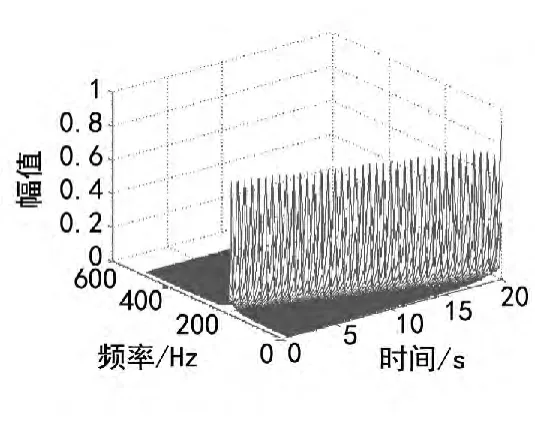
图1 仿真数据短时傅立叶处理结果(三维图)

图2 仿真数据短时傅立叶处理结果(时间-频率)图

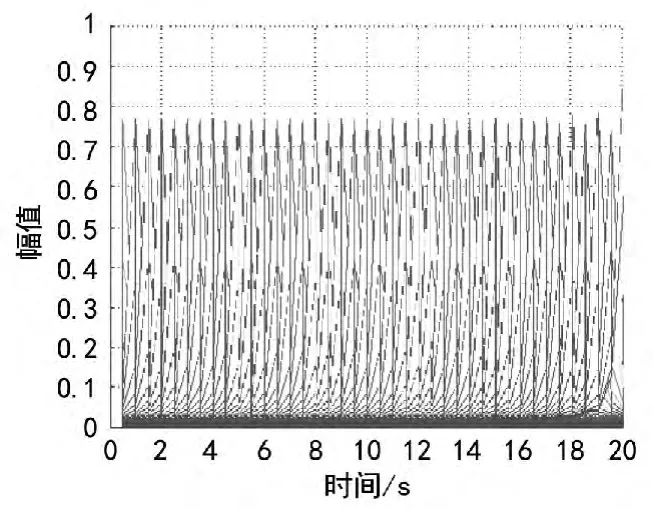
图3 仿真数据短时傅立叶处理结果(时间-幅值)图

从短时傅立叶处理结果来看，采用短时傅立叶变换的方式处理该仿真数据，可对发动机转子频率进行较为准确的跟踪，但是该方法得到的转速频率对应的幅值与仿真数据的理论值有着较大的误差，仿真数据的振动幅值为1，而从图3可看出，短时傅立叶变换方法得到的幅值不足0．8，误差大于20%。

2．2 采用等角度方法处理仿真数据

现采用等角重采样方法对该仿真数据进行分析，处理结果如图4～7所示。

图4 仿真数据短时等角度重采样处理结果(三维图)

图5 仿真数据短时等角度重采样处理结果(时间-阶次)

从图4～7的处理结果可看出，采用等角度重采样的方法处理该仿真信号，可以准确的对振动信号的频率进行跟踪，而且从图6可看出，该方法可以非常准确的得到转速对应频率的幅值，与短时傅立叶变换的处理方法相比，有着非常明显的优势。

图6 仿真数据短时等角度重采样处理结果(时间-幅值)

图7 仿真数据短时等角度重采样处理结果(阶次-幅值)

3 对航空发动机实际振动数据进行分析

在某型发动机试飞过程中，曾经发生发动机空中停车故障，现提取该发动机空中停车期间的振动数据，分别采用短时傅立叶和等角度重采样的方法对该数据进行分析。

从采用短时傅立叶分析结果图谱可看出在整个发动机空中停车的过程中，燃发器和动力涡轮的转速在迅速降低，这一点在图10上可清晰的表现出来，在图8三维图谱上也可看到在这个过程中，燃发器和动力涡轮对应的频率分量振动幅值也迅速减小，而在图9和图11上可在发动机停车过程中，振动最大值接近 3．5 g。

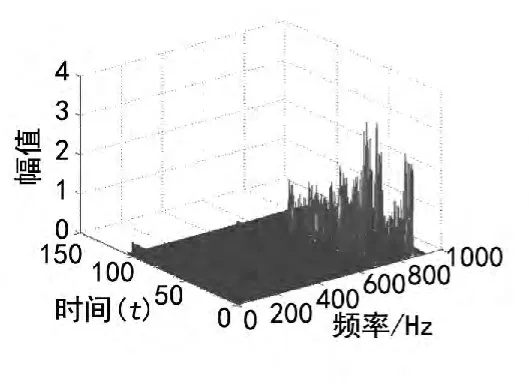
图8 短时傅立叶处理三维谱图

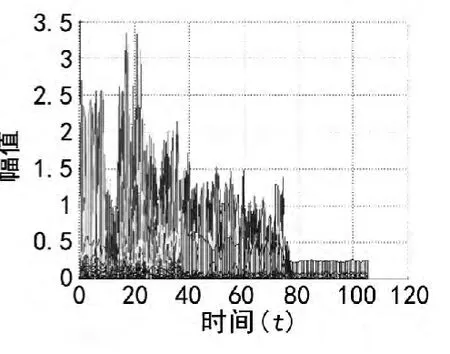
图9 短时傅立叶处理时间-幅值图

图10 短时傅立叶处理频率-时间图

图11 短时傅立叶处理频率-幅值图

图12 ～17为采用等角度重采样方法对振动数据分析结果，从图12和图13两个三维谱图上可看到，与短时傅立叶变换相比，采用等角度的方法可更清晰的看到燃发器和动力涡轮的振动变化情况，在图上可看出，随着发动机转速降低，燃发器和动力涡轮频率分量的振动值也在减小，但减小速度并不像短时傅立叶所显示的那么迅速，而且从图14和图15可看出在整个过程中，燃发器和动力涡轮最大振动值都为5．1 g左右。

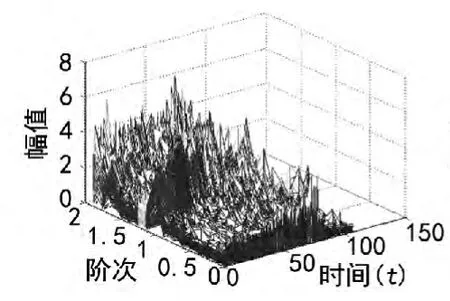
图12 对燃发器等角度分析三维图谱

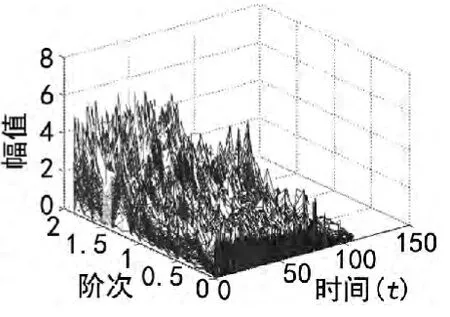
图13 对动力涡轮等角度分析三维图谱

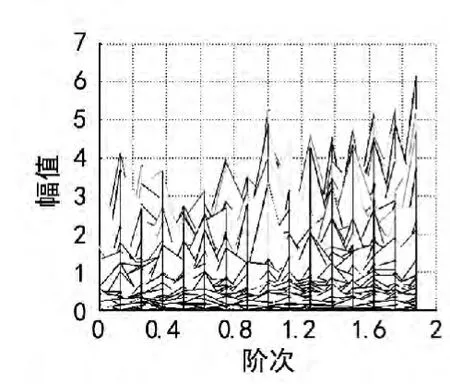
图14 对燃发器等角度分析阶次-幅值图谱

图15 对动力涡轮等角度分析阶次-幅值图谱

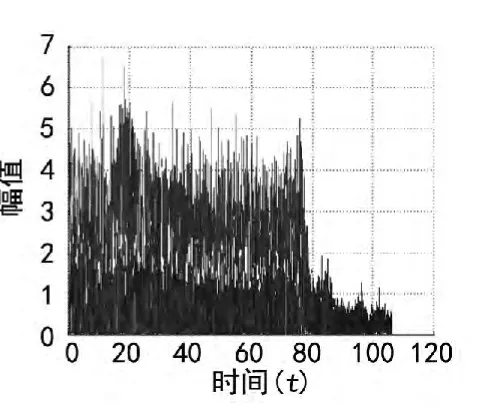
图17 对动力涡轮等角度分析时间-幅值图谱

根据仿真计算的经验，在处理发动机过渡态时，采用重采样的方式计算出的振动幅值更为准确，因此在这个过程中，发动机的最大振动值应该是5．1 g左右而不是短时傅立叶分析出的3．5 g结果，而且在这个发动机停车过程中，发动机的振动在逐渐下降，但是下降速度应该较缓慢。

4 总结

采用等角度采样对发动机过渡态振动数据进行分析，可得出结论:

(1)采用等角度的方法可以更清晰的看到燃发器和动力涡轮的振动变化情况。

(2)采用等角度的方法可以更为准确的得到发动机的振动幅值，而采用短时傅立叶的做法会缩小振动幅值，有可能错过发动机振动超限的故障。

［1］ Antonia J，Bonnardot F．Cyclostationarymodeling of Rotatingmachine Vibration Signals［J］．Mechanical Systems and Signal Processing，2004(18):1285-1314．

［2］ 傅俊庆，廖坤鹏．转速随机波动旋转机械振动信号的周期平稳性［J］．长沙理工大学学报，2006，3(4):49-53．

［3］ Remond D，Mahfoudh J．From Transmission Error Measurements to Angular Samp Ling in Rotating Machines with Discrete Ge2 Ometry［J］．Shock and Vibration，2005(9):1-13．

［4］ 杨炯明．旋转机械阶比分析技术中阶比采样实现方式的研究［J］．重庆大学学报，2004，16(3):249-253．

［5］ 孔庆鹏．发动机变速阶段振动信号时频分析阶比跟踪研究［J］．振动工程学报，2005，18(4):448-452．

［6］ 李 辉，郑海起，唐力伟．基于阶次跟踪和变换时频谱的轴承故障诊断［J］．振动、测试与诊断，2010，30(2):125-128．