初中几何教学略谈

王爱萍(河北省盐山县常庄中学　061300)

初中几何教学略谈

王爱萍(河北省盐山县常庄中学061300)

本文围绕几何直观概念与设计上课场景两点展开论述，诠释了其中的几点细节，教海浩瀚，一点经验之谈，管窥蠡测，分享同仁。

初中几何直观创新绘图上课场景

一、在教学当中发挥几何直观的概念

(一)需要解决的问题

世界是数学的'数学推动着社会的前进。教学讲课时'我们教育者一心营职'全力以赴'但当我们面对数学这门奥秘的学科的时候'如何去解决教学当中的难题?如何在数学思维当中'培养学生的“几何直观”的概念?如何让学生的情景思维逻辑转化为真正运用图文并茂的方式在脑海当中培养出新的解决问题的思维的形式?

(二)利用绘图解答疑难

面对数学当中的难点问题时'我们以往的做法是通过公式证明出来。我们现在不仅要培养学生解决难题的思维'还要教会学生把数学当中的难题利用绘图来证明。这是许多数学教师在以前都很难想到的'比以往的传统的教学更加科学和规范。面对教学当中的难题'我们可以尝试通过画圆去证明。在一个图形当中'我们可以通过垂直等分线去判断、去证明。

(三)理清思路

当我们发现一个问题的时候'需要把问题先理清理顺。只有在解决难题当中'先分析问题'才能更好地去证明。那么我们面对数学证明的难题时'就需要用绘图的方式表现出来'当我们用图画的形式直观地表现出来'学生就会十分感兴趣。面对一个几何难题的时候'许多学生通过看图识画就能想到如何去解题'这样学生就会对解题产生兴趣'教师的课堂教学也会更加生动有趣。

(四)想方设法提高学生的积极性

面对数学当中提出的新观念——几何直观'我们可以通过几何的观点去看待。在做证明题时'我们以往的方式是通过文字的思维去分析和判断。现在我们有了几何直观的新观念'可以通过圆规、直尺更加清晰地画出图形去进行分析。这样我们在证明几何难题的时候'能更快地得到几何难题的答案。当题目学生都能自己解答后'慢慢地'学生的学习兴趣和学习信心就可以培养出来'进而也就会更加积极地去学习数学。所以'教师可以利用这个方法来促进学生对数学学习的积极性。

(五)在教学中养成良好的画图习惯

几何直观是具体的'它与许多重要的数学内容紧密相连'如分数的认识'负数的认识等。教师要从思想上认识到它的重要性'并把它当做是最基本的能力去培养学生。在日常的教学中'我们要帮助学生从小养成良好的画图习惯。在教学中'教师要通过多种途径和方式使学生真正体会画图对于理解概念、寻求解决思路带来的益处。要求学生解决问题时'能画图的尽量画图'将相对抽象的思考对象“图形化”'尽量把数学的过程变得直观'直观了就容易展开形象思维。

二、设计上课场景

学习初中数学对称图形'针对“几何直观意识和能力的培养”设计上课场景。

1.题目类型:对称图形章节的重点和难点知识'结合对称点求两点间的最短距离。

2.做题技巧:配合图形'用作图引出解题思路'形成解题答案。

3.方法优点:便于理解'达到一次理解'长时间不忘'并能灵活运用。

4.题目:如图一个人从点P出发'到条形草地OA处让马吃草'然后到河流OB处让马喝水'最后回到点P处'他该怎么走行程才能最短?

5.解题分析:这类题型通过作图、看图更能直观得到解题思路和解题办法。

6.解题过程:要找到从点P到OA再到OB后回到点P的最短路径'我们作图如下:

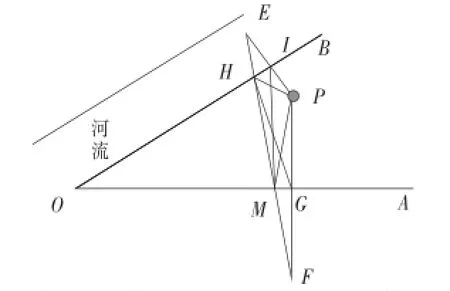
如图分别做出点P以OA、OB为对称轴的对称点F、E'并交OA、OB于点G、l'连接FE交OA、OB于点M、H。连接PM和PH'则最短路径从点P到点M再到点H最后回到点P，即:PM+MH+HP。

7.原因分析:由对称点性质得MF=MP' HE=HP'则可以将马要走的路径△PMH展开为一条直线EF。由两点间直线距离最短得到直线EF为最短距离。

8.疑问分析:同学们是不是要提出疑问了'不是点到直线间距离'垂线段距离最短吗?那最短距离应该是PG+Gl+lP呀!下面我们还结合图形还分析'从图中我们可以看出'在△HGF中'PG+HG=HG+GF>HF=PM+MH。而由于点I的位置关系'Gl>HG。同理'在△ElM中' Pl+lM=El+lM>EM=EH+HM。而由于点I的位置关系'Gl>lM。

根据图形可见'走△PMH距离最短。

学生会发现通过作图分析这样的题型'更有利于我们轻松找到解题思路和解题办法'更便于记忆'更有利于我们找到快速有效的学习方法。

总之'在教学过程中'促进学生对知识充满好奇心'对新旧知识能更好地融会贯通'对新知识能更快地消化吸收'让学生学起来不感觉吃力'使课堂上有其乐融融的学习情境'形成学生良好的思维习惯、应用意识和探索数学的能力与精神'让他们的数学素质不断提升。

(责编赵建荣)