随机波作用下海床动态响应分析
2015-11-22江俊达周香莲
张 军,江俊达,华 莹,周香莲
(1.上海交通大学 海洋工程国家重点实验室,上海 200240;2.上海交通大学 船舶海洋与建筑工程学院 海洋岩土工程研究中心,上海 200240)
通常的海床动态响应模拟都是使用确定意义上的规则波理论,实际的海洋波浪在一定的时间及地点、波浪的出现以及波浪的参数都有着很强的随机性。前人的研究大多使用线性波、Stokes 波或者椭圆余弦波。Hsu 和Jeng[1]研究了波浪作用下细砂质海床的动态响应问题。Zhou 等[2-3]建立了波流联合作用下的多层海床模型,研究了渗透系数、孔隙率和波高等对孔压及有效应力的影响,并分析了液化范围和各向异性的海床在波浪作用下的动态响应。Xu 等[4-5]提出了准确计算一阶椭圆余弦函数的近似表达式和使用条件,并使用静态Biot 固结模型进一步研究了椭圆余弦波作用下,多孔介质海床的孔压以及有效应力的分布。对于随机波的模拟,Longuet-Higgins[6]采用分析电子管噪声电流的方法,对线性波浪进行叠加模拟随机波的传递。对于不同的海况,采用不同的频谱对随机波进行描述[7-9]。目前用随机波对海床动态响应进行的计算,大都使用Biot 固结模型[10-12],忽略了流体速度及土体位移加速度影响。如,Xu[13]使用简化的随机波模拟了海床的液化进程。
为了反映波浪真实性,采用Longuet-Higgins 模型线性波浪叠加法模拟随机波浪(使用Jonswap 谱)。验证随机波浪后,用动力u-p 模式建立海床动态响应模型,联合随机波浪、u-p 有限元模型,用COMSOL Multiphysics 的PDE 模块写入控制方程求解,得到多孔弹性海床的孔压和有效应力。将随机波、Stokes 波和椭圆余弦波结果进行对比后对渗透系数和饱和度进行了参数分析。
1 随机波浪理论及海床动态响应模型的建立
1.1 随机波理论
采用Longuet-Higgins 模型,将固定点的海浪波面位移表示为如下随机过程:

式中:M 为组成波的数量,数值充分大;i 为组成波的序列;d 为水深;ki为第i 个组成波的波数;ai表示第i 个组成波的幅值;ζi为第i 个组成波的随机相位值,均匀分布于(0,2π);表示代表频率,均匀分布于(fi-1-fi)或由式(2)计算,fi为第i 个组成波的频率。组成波的波面幅值ai可由随机波频谱S(f)求得,波数ki、频率和水深d 的关系可以用下式表示(g 为重力加速度):

而对于频谱S(f),采用改进的Jonswap 型谱,此谱的优点在于给定了γ 即可由设计波要素确定谱形:
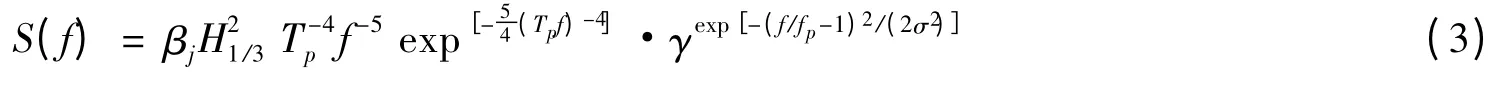
其中,

式中:γ 为增强因子,取1 ~7(平均值为3.3);fp为频谱峰值对应的波浪频率,取值可以由fp=1/Tp求得;同时认为f 的取值在0 ~5fp之中均匀分布;σ 的取值依赖于f 的取值,f >fp时,σ=0.07,否则取为σ=0.09;TH1/3和H1/3分别为波浪有效周期和有效波高。
随机波作用下海床受到的波压力pb为

1.2 海床动态响应分析模型以及验证
1.2.1 计算模型的建立
计算模型如图1 所示,水深为d,厚度为h 的海床下为固定的不透水基层,有效周期为TH1/3,有效高度为H1/3,随机波沿x 轴正向传播。
1.2.2 控制方程与边界条件
多孔弹性海床考虑超孔隙水压力和土骨架变形下Biot方程可以表示为

式中:p 为孔隙水压力;γw为孔隙流体的重度;n 为海床土壤孔隙率;Kz为土壤渗透系数;ρf为流体的密度;β 为孔隙流体的压缩性系数;ε 为土体体积应变。β,ε 分别由以下两式定义:

图1 随机波作用下海床动态响应计算模型Fig.1 Diagram of a seabed under random waves

其中,kw为孔隙水的体积模量,通常取kw= 2 ×109N/m2;S 为海床土体的饱和度;u 和w 分别为土体位移在水平及竖直方向上的分量;Pw0为孔隙水绝对压力。
考虑土体位移加速度,忽略与相对孔隙流体位移相关的惯性项得到u-p 形式的控制方程:

式中:σij为土体总应力;ρ 和ρf分别是土体和孔隙流体的密度;为土体骨架的加速度;为孔隙流体相对于土体骨架的平均位移;即为相对平均加速度;Kf为孔隙流体的体积模量。
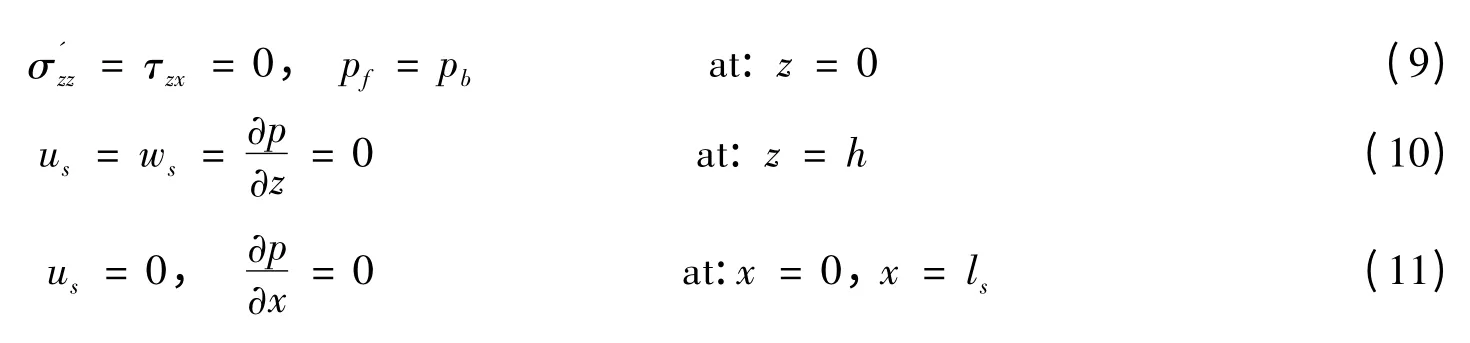
2 模型验证及结果分析
2.1 模型验证
如图2 所示,使用Jonswap 谱频谱曲线与Jeng[11]的结果相比(取TH1/3=10 s,H1/3=6 m,d =25 m),无论是峰值还是谱宽都吻合良好,可以使用。为了进一步验证u-p 模型,将结果与解析解(Liu 和Jeng[10])比较,具体取值见图3 所示,其中实线为当前模型,虚线为解析解。可见本结果与解析解相比,波面压力值几乎相同,变化趋势基本相同,存在差异主要因为这里用Biot 动态模型,考虑流体速度及土体位移加速度,而Liu 和Jeng 用的是Biot 固结模型,忽略流体速度及土体位移加速度的影响。
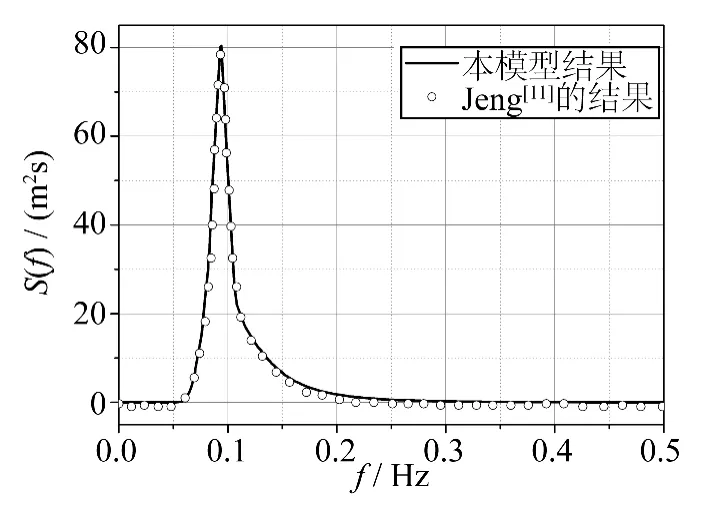
图2 本文结果与Jeng[11]结果对比Fig.2 Comparison between the present results and Jeng[11]

图3 当前模型和解析解(Liu and Jeng[10])的比较Fig.3 Comparison of previous results (Liu and Jeng[10])
2.2 结果分析
2.2.1 不同波浪理论下海床动态响应分析
本部分将模拟得到的一阶Stokes 波、椭圆余弦波、随机波与海床动态响应模型结合,得到同样波浪参数下(参数见表1,Stokes 波及椭圆余弦波的波高取2 m,与随机波的H1/3相同)不同波浪理论单位化后的孔压及有效应力随海床深度变化的响应曲线,均取各自表面最大波动水压力剖面分析,单位化参数P0=ρwgH1/3。椭圆余弦波的模拟将在另一篇文章详述。如图4 所示,在孔压最大的截面上海床表面受到波动水压力,椭圆余弦波为0.68,大于随机波0.51,Stokes 波最小为0.43。孔压变化趋势基本相同,均在开始阶段剧烈衰减,达一定深度后衰减减缓,随海床深度加深逐渐稳定,最终稳定值椭圆余弦波大于随机波,Stokes 波最小。图5表明有效应力绝对值的最大值Stokes 波(-0.41)最早达到,然后是椭圆余弦波(-0.27)以及随机波(-0.26),变化趋势也基本相同。可见使用不同波浪理论对海床表面的孔压初值将产生明显的影响,且最大有效应力出现在海床某深度处,不可简单用Stokes 波或线性波计算。

表1 计算参数的选取Tab.1 Parameters selected in present model

图4 不同波浪理论下孔压随海床深度的变化Fig.4 Distribution of pore pressure (p /P0)versus seabed depth with different wave theories

图5 不同波浪理论下有效应力随海床深度的变化Fig.5 Distribution of vertical stress (σzz’/P0)versus seabed depth with different wave theories
2.2.2 渗透系数Kz对结果影响的分析
渗透系数一直是海床动态响应研究很关注的参数,由图6 可见随着渗透系数减小(Kz=0.1、0.01、0.001 m/s),孔压衰减更平缓。有效应力绝对值最大值随渗透系数减小而增大,达最大值的深度则相对更浅(图7)。由此结果可知工程上可通过改变渗透系数达到改变动态响应及液化状况的目的。如图8 所示,取4个周期的时长(32 s)及1/10h 的海床深度观察不同渗透系数下,固定点孔压随时程的变化,由于波浪作用的随机性,固定点的孔压变化也表现出随机性,而随着渗透系数的增大,固定点的孔压表现出正相关的增大。
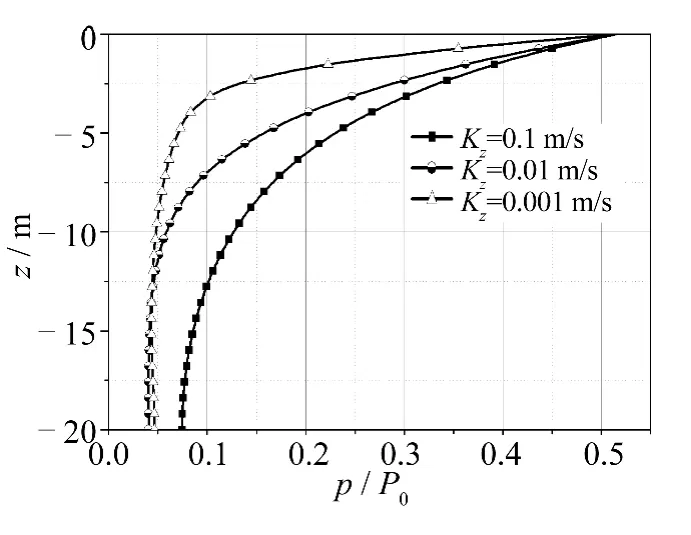
图6 不同渗透系数下孔压随海床深度的变化Fig.6 Distribution of pore pressure (p /P0)versus seabed depth with different permeability coefficients
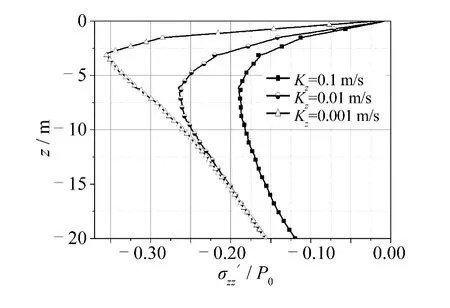
图7 不同渗透系数下有效应力随海床深度的变化Fig.7 Distribution of vertical stress (σzz' /P0)versus seabed depth with different permeability coefficients
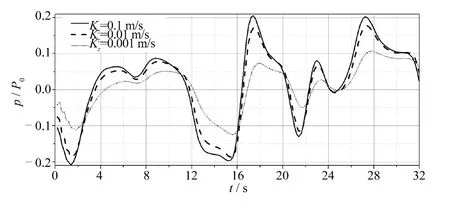
图8 不同渗透系数下1/10h 深度固定点孔压随着时程的变化Fig.8 Time varying pore pressure (p /P0)distruibution for different permeability coefficient at z=1/10h
2.2.3 饱和度S 对结果影响的分析
饱和度是海床的重要参数,如图9 所示,虽然随着饱和度的减小,整个孔压随着海床深度变化的趋势没有发生改变,但是孔压变化衰减速度明显增快。由图10 可知,有效应力绝对值达到的最大值随着饱和度的减小而增大明显,随着饱和度从1 变化到0.98 再变化到0.96,有效应力绝对值从0.17 增大到0.26 再增大到0.30。同样取4T 周期以及1/10h 的深度,研究固定点的孔压及有效应力随着时程的变化,图11 中可知随着饱和度的增大,固定点的孔压保持随机性的同时也相应增大。可见饱和度对孔压和有效应力影响明显,在对海床动态响应的计算或者洋底结构物的设计过程中,通过实验确定饱和度时需要保证精度。

图9 不同饱和度下孔压随海床深度的变化Fig.9 Distribution of pore pressure (p /P0)versus seabed depth with different saturation degrees

图10 不同饱和度下有效应力随海床深度的变化Fig.10 Distribution of vertical stress (σzz'/P0)versus seabed depth with different saturation degrees
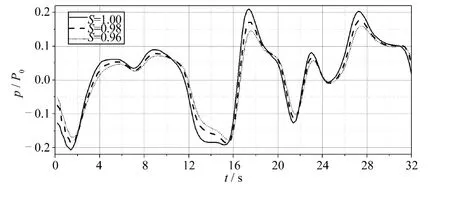
图11 不同饱和度下1/10h 深度固定点孔压随着时程的变化Fig.11 Time varying pore pressure (p /P0)distruibution for different saturation degrees at z=1/10h
3 结 语
1)使用不同的波浪理论对海床表面的孔压初值有明显影响。使用Stokes 波计算的海床表面的波动水压力大于椭圆余弦波,随机波最小。Stokes 波最早达到有效应力绝对值的最大值,然后是椭圆余弦波和随机波,达到最大值的海床深度也是同样顺序渐增。简单使用线性波或Stokes 波等模拟复杂的海洋情况将造成较大误差。
2)随着渗透系数的减小,孔压的变化趋势并未改变,但使得排水难度增大,影响深度减小,导致孔压减小。另一方面,有效应力绝对值最大值随着渗透系数的减小呈增大趋势,达到最大值的深度则相对更浅。1/10h海床深度的固定点孔压随着渗透系数的减小而表现出正相关的增大。有效应力的数值则相应减小。
3)随着饱和度的减小,孔压变化衰减速度明显增快,且海床底部的稳定孔压值也相应减小。有效应力绝对值达到的最大值随着饱和度的减小而增大明显。1/10h 深度的固定点的孔压随着饱和度的增大而相应增大。而有效应力则随着饱和度的增大而减小。
[1]HSU J R C,JENG D S.Wave-induced soil response in an unsaturated anisotropic seabed of finite thickness[J].International Journal for Numerical and Analytical Methods in Geomechanics,1994,18:785-807.
[2]ZHOU X L,XU B ,WANG J H,et al.An analytical solution for wave-induced seabed response in a multi-layered poro-elastic seabed[J].Ocean Engineering,2011,38(1):119-129.
[3]ZHOU X L,Wang J H,ZHANG J,et al.Wave and current induced seabed response around a submarine pipeline in an anisotropic seabed[J].Ocean Engineering,2014,75:112-127.
[4]XU Y F,XIA X H,WANG J H.Calculation and approximation of the cnoidal function in cnoidal wave theory[J].Computers& Fluids,2012,68:244-247.
[5]XU Y F,XIA X H,WANG J H,et al.Numerical analysis on cnoidal wave induced response of porous seabed with definite thickness[J].Journal of Shanghai Jiaotong University,Science,2013,18:650-654.
[6]LONGUET-HIGGINS M S.The statistical analysis of a random,moving surface[J].Philosophical Transactions of the Royal Society of London,Series A,Mathematical and Physical Sciences,1957:321-387.
[7]HASSELMANN K,BARNETT T P,BOUWS E,et al.Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP).1973.
[8]HUANG N E,LONG S R,TUNG C C,et al.A unified two-parameter wave spectral model for a general sea state[J].Journal of Fluid Mechanics,1981,112:203-224.
[9]WEN S H,ZHANG D C,CHEN B H,et al.Theoretical wind wave frequency spectra in deep water I.Form of spectrum[J].Acta Oceanologica Sinica,1998,7(1):1-16.
[10]LIU H,JENG D S.A semi-analytical solution for random wave-induced soil response and seabed liquefaction in marine sediments[J].Ocean Engineering,2007,34(8):1211-1224.
[11]JENG Dongsheng.Porous models for wave-seabed interactions[M].上海:上海交通大学出版社,Springer,2013.
[12]王忠涛,栾茂田,JENG Dongsheng,等.随机波浪作用下海床动力响应及液化的理论分析[J].岩土力学,2008,29(8):2051-2056.(WANG Zhongtao,LUAN Maotian,JENG Dongsheng,et al.Theoretical analysis of random wave-induced seabed response and liquefaction[J].Rock and Soil Mechanics,2008,29(8):2051-2056.(in Chinese))
[13]XU H.Wave-induced liquefaction processes in marine sediments[D].University of Dundee,2012.
