冲击荷载作用下新型延展式张力腿平台时域分析
2015-11-22黄维平
巩 超,黄维平
(中国海洋大学 工程学院,山东 青岛 266100)
随着海岸和浅海海域油气资源的枯竭,海洋油气开采逐步向深水甚至超深水进军[1],因此在海洋工程行业中需要不断研发新型海洋结构来适应更加严酷的海洋条件。张力腿平台(TLP)是一种垂直系泊的半顺应半刚度式平台,由甲板、主体和锚泊系统三部分组成,锚泊系统是由垂直张力腿组成,使平台与海底相连,从而限制垂荡运动,从而能够在平台上使用干采油树[2]。张力腿平台垂荡运动的固有周期一般为2 ~4 s,纵横荡运动的固有周期为100 ~200 s,纵摇、横摇固有周期均低于4 s,艏摇运动的固有周期高于40 s,整个结构的频率跨越波浪的一阶频率两端,可以避免结构和海洋能量集中的频率发生共振。
Ahmad[3]研究了TLP 在随机波海浪谱下的耦合响应,同时考虑了不同浸水、浮力和垂直方向波浪力引起的张力变化等各种非线性效应,考察了张力变化引起的次谐波共振,同时也考察了变化浸水效果引起的次谐波共振。Chandrasekaran 等[4]研究了随机波载荷下三角形TLP 的动态响应,对六个自由度响应进行了谱分析得出响应规律,同时考虑耦合、可变浸水以及流的影响。Tabeshpour 等[5]在时域和频域中对TLP 进行了非线性动态分析,随机波的时间历程基于PM 谱,随机波以任意浪向角作用在结构上。余建星等[6]分析了平台总体响应分析的基本方法,包括频域分析和时域分析的方法,将不同的分析技术相结合,提供了不同的分析策略,为张力腿平台总体响应分析的深入研究提供了一定的基础。“典型深水平台概念设计研究”课题组[7]以1 000 m 水深TLP 平台为例,详细叙述了TLP 平台水动力分析的过程和方法,包括有限元模型的建立,水动力特征的计算,水动力载荷响应的计算以及运动响应分析。
文中提出了一种新型的延展式张力腿平台,新型平台由四个立柱和一个环形浮箱连接而成,环形浮箱是由四个箱型梁焊接而成。与传统延展式张力腿平台相比,由于延展结构与浮箱成为一体结构,新型平台分块少,接口焊缝少,而且延展结构的接口焊缝也不需要考虑。参考以上研究对新型延展式张力腿平台进行风、浪、流环境荷载的综合作用和平台、张力腿的相互耦合作用下的时域耦合分析,同时模拟波浪破碎作为冲击荷载,研究了新型平台在冲击荷载作用下的运动位移时程、张力腿系统张力时程等结果,通过分析证明新型延展式平台有良好的运动响应。
1 新型延展式平台的设计和尺寸
1.1 新型平台的设计
新型延展式张力腿平台(ETLP)由上部组块、主体和张力腿系统组成,其中主体依然由浮箱和立柱组成。基于所选环境条件和上部甲板重量确定采用四立柱形式,浮箱是由四根箱型梁焊接而成,每个箱型梁的一端焊接到另一根梁梁长四分之一处,另一端为自由端,距其梁长约四分之一与另一梁焊接相连。立柱截面为方形截面,只要方立柱上的圆角足够大(r≈D/4)就能达到大多数圆立柱的水动力性能的优势,尽管大部分采用圆立柱,但是总体趋势是采用方立柱,影响截面选择的主要因素的浮箱、立柱及张力腿的连接方式,平台采用12 根张力腿系泊,张力腿连接在浮箱自由端的外侧,每一个自由端处连接三根张力腿。新型ETLP 的四个延展结构与浮箱为整体结构,从而只有8 个分块结构,与传统结构相比减少了4 个分块,其对比结构示意如图1 和图2 所示。
新型ETLP 中延展结构就是浮箱的一部分,这不仅解决了延展结构的连接问题,而且延展结构与浮箱成为一体结构,改善了延展结构的强度和疲劳可靠性问题。

图1 传统延展式张力腿平台Fig.1 Traditional extended tension leg platform

图2 新型延展式张力腿平台Fig.2 New extended tension leg platform
1.2 新型平台的尺寸
根据平台的设计依据,初步选择平台主体结构尺寸,平台的主尺寸如表1 所示。

表1 新型延展式张力腿平台参数Tab.1 New ETLP specifications
2 时域耦合计算方法
工作在海面上的平台受到风、浪、流等环境荷载的综合作用,有时还会遇到极端环境条件,平台运动响应主要指正常工作条件下平台六个自由度的运动响应,直接影响到平台的正常作业。时域下的分析预报是预报波浪上海洋结构物运动响应的经典方法。
2.1 时域运动控制方程
2.1.1 风荷载
风选取NPD 风谱进行模拟,表达式:

式中:SNPD(f)为风能谱密度,f 是频率,U0是海面以上10 米处一小时的平均风速,z 是海面以上标高,U(z)是在高度为z 处的平均风速。
根据ABS 规范[8],风载荷可以定义:

式中:α =0.611,Vk则为风速,Ch指直接承受风荷载的平台构件的高度系数,Cs为平台构件的形状系数,A 为平台构件的投影面积。
2.1.2 流荷载
海洋中海洋结构物将受到海流的作用,流作用下结构物受到的力和力矩表达式:

式中:V 为流相对于平台的速度;ρw为流体密度;A 为平台在流速方向上的投影面积;Cdc为流阻力系数;L为力作用点到平台重心的距离。
2.1.3 时域运动方程
各种载荷下,考虑系泊系统的平台时域运动方程:
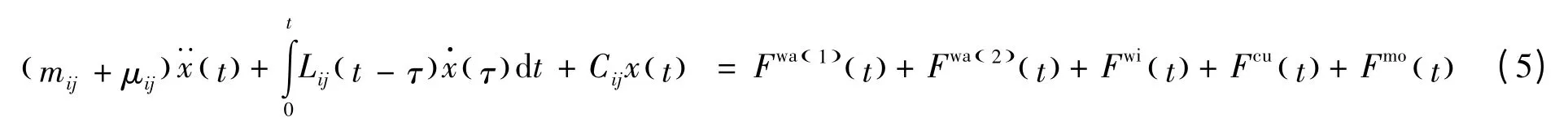
式中:Fwa(1)( t )、Fwa(2)( t )、Fwi( t )、Fcu( t )和Fmo( t )分别为一阶波浪荷载、二阶波浪荷载、风荷载、流荷载和系泊缆张力时程;mij为平台的质量矩阵;μij为附加质量矩阵;Cij为恢复力系数矩阵;Lijt (-τ) 为系统的时延函数。
已知频域内浮体运动的附加质量系数μij(ω) 和阻尼系数λij(ω) ,有:

时延函数表达式:

2.2 动响应耦合分析
耦合分析中,将平台和张力腿系统作为一个整体系统进行时域的动态耦合计算。离散化的张力腿系统耦合运动方程[9]:

式中:RI(x,t),RD(x,t),RS(x,t),RE(x,t)分别为惯性力矢量、阻尼力矢量、内力矢量、外力矢量。
惯性力矢量为:

式中:Ms为平台及系泊系统的质量矩阵,包括结构本身的质量和附加质量。
阻尼力矢量为:

式中:Cs为系统阻尼矩阵,包括内结构阻尼和水动力阻尼。RS(x,t)的计算基于单元的每一瞬时的应力状态,RE(x,t)包括重力和浮力、锚链与海底作用力、海洋环境力和特定作用力。
求解平台的时域运动方程时,要充分考虑张力腿的作用力对平台运动的影响;而在进行张力腿动力计算时,必须以平台的运动和位移作为边界条件。总的来说,张力腿的存在限制了平台的运动,而平台的运动又导致了张力腿系统的非线性变化,因此必须将二者联合起来进行耦合分析,通过迭代求解,求得整个系统在每一时刻的运动、位置和受力情况[10]。
2.3 冲击荷载计算
深水条件下,当波陡大于1/7 也会发生波浪破碎,此时,波高超过波长的14%。DNV[11]规范建议:对破碎波荷载应区分崩碎波(spilling)、卷碎波(plunging)和激碎波(surging)而采用不同的公式计算。这里选择的破碎波类型为崩碎波,用小振幅波计算相关波浪参数。
对于卷碎波(plunging),其作用在圆柱体上的冲击荷载可按下式计算:

式中:CS为砰击系数,对于光滑的圆柱体,3.0 ≤CS≤2π,DNV 规范建议取CS=5.15;ρw为海水密度;A 为砰击力的作用面积;v 为水质点与圆柱体的相对速度。
如果卷碎波正好在垂直圆柱体前破碎,则冲击力的持续时间可按下式计算:

式中:c 为波速;D 为圆柱体直径。
对于激碎波和崩碎波,冲击荷载和砰击系数CS分别按下式计算:
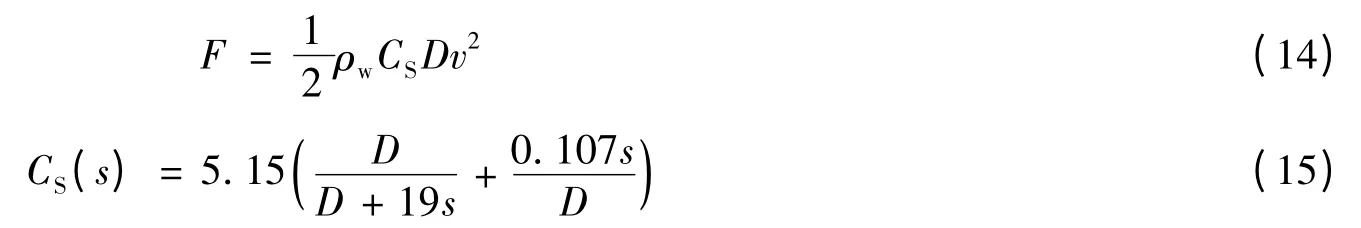
式中:s 为穿透系数,表示破碎波浸没圆柱体的距离,0 <s <D。冲击开始时,s =0,CS(0)=5.15;当圆柱体全部浸没在破碎波中,s=D,CS(D)=0.8。
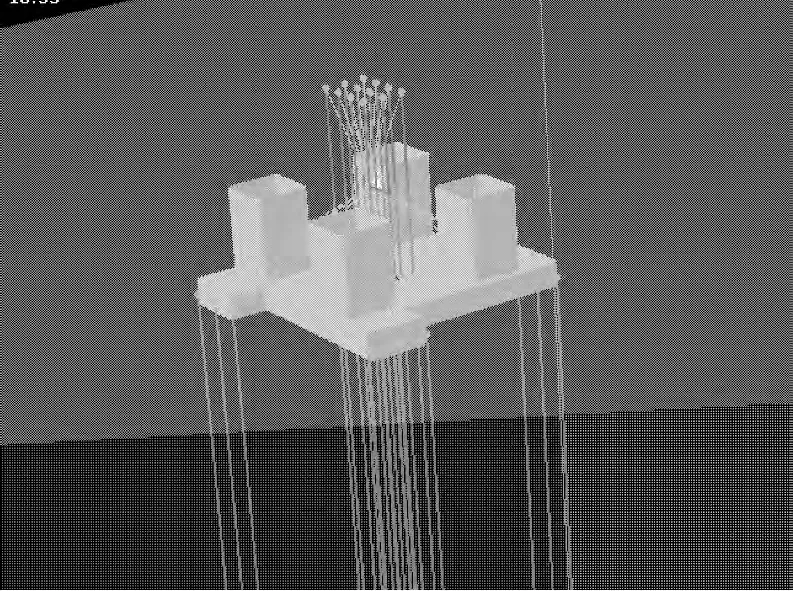
图3 新型延展式张力腿平台耦合模型Fig.3 New ETLP coupling model
3 时域耦合分析计算结果
建立新型延展式张力腿平台分析模型,考虑风浪环境载荷,在时域内进行了计算分析,得到了新型延展式张力腿平台的波浪时程、平台运动响应以及波频运动响应时程。
图3 为时域分析时延展式张力腿平台与张力腿系统的耦合分析模型。采用SESAM 软件Deep C 模块对新型延展式张力腿平台在南海环境条件下进行了时域耦合分析,分析时长10 800 s,间隔0.5 s。时域分析中采用南海海域百年一遇海洋环境条件,选取平台迎浪情况的计算结果进行研究,百年一遇海洋环境条件如表2 所示。

表2 南海海域百年一遇环境参数选取Tab.2 Once-in-a-century environment parameters selection
3.1 运动响应耦合分析结果
延展式张力腿平台运动时程主要指六个自由度的运动响应结果,对张力腿平台而言,其水动力性能与响应有密切的联系,因而应将平台的响应尽量控制在一个可以接受的范围内。按照钻井作业对平台摇荡的要求,一般规定浮动式平台运动响应设计值:摇摆≤±3°,升沉≤±1 m,漂移≤工作水深的5%[7]。
图4 分别为延展式张力腿平台的纵荡、横荡、垂荡、横摇、纵摇和艏摇的波频时程曲线。从平台时程曲线可知,平台水平面内的偏移量极值出现在纵荡的时程结果中,时间在3 400 s,极值为-30.45 m,为水深的2.03%;平台的摇摆角度极值出现在纵摇的时程结果中,时间在8 000 s,极值为-0.44°;平台的升沉出现在垂荡时程的9 000 s,极值是-0.89 m,满足设计要求。
通过时域耦合分析得到12 根张力筋腱的应力时程曲线,通过比较得知发生最大应力的筋腱为4 号筋腱,其张力时程曲线如图5 所示。筋腱所用钢材型号为NV-32,屈服极限为315 MPa。由图可知最大筋腱张力值出现在筋腱张力时程的8 000 s,为3.06 ×107N。此时筋腱应力σ =Tmax/A =259.93 MPa,小于筋腱的最大拉应力315 MPa×0.9 =283.5 MPa,因此张力筋腱的强度满足安全要求。


图4 延展式张力腿平台时程曲线Fig.4 Time domain result of ETLP
3.2 冲击荷载作用下的耦合分析

图5 4 号张力筋腱张力时程Fig.5 No.4 tendon’s tension time domain result
根据文中提出的理论计算得出深水破碎波作用在平台立柱上的的数值和作用时间,在输入百年一遇南海环境条件之后,将深水破碎产生的荷载作为冲击荷载作用在平台模型上,方向为0°,得到平台在冲击荷载作用下的时域耦合结果。
图6 分别是延展式张力腿平台的纵荡、横荡、垂荡、横摇、纵摇和艏摇的波频时程曲线。从平台时程曲线可知,平台水平面内的偏移量极值出现在纵荡时程结果中,时间在3 400 s,极值为-30.53 m,为水深的2.04%;平台的摇摆角度极值出现在纵摇时程结果中,时间在3 400 s,极值为-0.46°;平台的升沉极值出现在垂荡时程的9 000 s,为-0.92 m,满足设计要求。

图6 冲击载荷作用下延展式张力腿平台时程曲线Fig.6 Demain result of ETLP under the impact load

图7 冲击载荷作用下4 号张力筋腱张力时程Fig.7 No.4 tendon’s tension time domain result
与正常百年一遇南海环境条件下的平台响应的不同之处,在于初始时刻,平台产生一个X 轴正向的位移,约为4.14 m,未超出平台平面内允许的最大偏移量。这是平台在初始时刻受到冲击荷载的作用而产生的位移。由于冲击荷载作用时间非常短暂,在随后的时程中,平台失去冲击荷载的作用,冲击荷载作用所致位移开始衰减,大约200 s 后,在张力筋腱的张力作用下回复至原时程响应位置。
同时,由图6 可知,其他五个自由度上的平台响应时程曲线分别与正常百年一遇南海环境条件下的响应曲线比较近似,故其时程响应受冲击荷载影响不大。
通过时域耦合分析得到12 根张力筋腱的应力时程曲线,通过比较得知发生最大应力的筋腱为4 号筋腱,其张力时程曲线如图7 所示。由图可知最大筋腱张力出现在筋腱张力时程的8 000 s,极值为3.06 ×107N。此时筋腱内的应力σ=Tmax/A=259.93 MPa,小于筋腱的最大拉应力315 MPa ×0.9 =283.5 MPa,因此张力筋腱的强度满足安全要求。
4 结 语
提出了一种新型延展式张力腿平台,利用环形浮箱以及浮箱与延展结构一体化减少了平台主体结构的连接焊缝和结构分块,避免了延展结构与立柱的连接,提高了平台的结构强度和疲劳可靠性。进一步通过对新型延展式张力腿平台和张力腿系统的时域耦合分析,证明了新型平台具有良好的运动响应,张力筋腱应力满足安全要求。同时通过模拟冲击荷载,得到平台在冲击荷载作用下的时程响应,结果表明新型平台的运动响应符合要求,对我国张力腿平台平台的研发和设计优化具有重要意义。
[1]李润培,谢永和,舒志.深海平台技术的研究现状和发展趋势[J].中国海洋平台,2003,18(3):1-5.(LI Runpei,XIE Yonghe,SHU Zhi.A review on the technical development of deep water offshore platform[J].China Offshore Platform,2003,18(3):1-5.(in Chinese))
[2]SUBRATA K,Chakrabarti.Handbook of offshore engineering[M].London:Elsevier Ltd,2005.
[3]AMAD S.Stochastic TLP response under long crested random sea[J].Computers & Structures,1996,61(6):975-993.
[4]CHANDRASEKARAN S,JAIN A K.Triangular configuration tension leg platform behavior under random sea wave loads[J].Ocean Engineeing,2002,29:1895-1928.
[5]TABESHPOUR M R,GOLAFSHANI A A,SEIF M S.Comprehensive study on the result of tension leg platform response in random sea[J].Journal of Zhejiang University,Science A,2006,7(8):1305-1317.
[6]余建星,张中华,于皓.张力腿平台总体响应分析方法研究[J].海洋通报,2008,27(2):97-102.(YU Jianxing,ZHANG Zhonghua,YU Hao.Research on TLP global response analysis method[J].Marine Science Bulletin,2008,27(2):97-102.(in Chinese))
[7]“典型深水平台概念设计研究”课题组.张力腿平台水动力响应分析[J].中国造船,2005,46(S):477-489.(The Group for Typical Deep Water Platform Conceptual Design.Hydrodynamic analysis for TLP[J].Shipbuilding of China,2005,46(S):477-489.(in Chinese))
[8]ABS,Rules for building and classing mobile offshore drilling units[S].2007.
[9]CUMMINS W E.The impulse response function and ship motions[M].Schiffstechnik,1962.
[10]陈新权.深海半潜式平台初步设计中的若干关键问题研究[D].上海:上海交通大学,2007.(CHEN Xinquan.Research on preliminary design of deepwater semisubmersible[D].Shanghai:Shanghai Jiao Tong University,2007.(in Chinese))
[11]DNV-OS-J101,Design of offshore wind turbine structures[S].2004.
