指标权重方法比较研究——以湄潭县基本农田划定为例＊<br/>

指标权重方法比较研究——以湄潭县基本农田划定为例＊

2015-11-22王爱平焱1李枋燕龙剑峰

贵州大学学报(自然科学版) 2015年2期

王爱平，周焱1，*，李枋燕，龙剑峰，陈洋，张慧

(1.贵州大学农学院，贵州贵阳 550025;2.贵州大学土地规划与信息技术研究所，贵州贵阳 550025;3.西南大学民族学院，重庆北碚 400715;4.贵州省国土资源勘测规划研究院，贵州贵阳 550004)

指标权重表示某一指标在总体指标体系中的相对重要程度，评价指标权重确定的合理性直接影响评价结果的可靠性和准确性［1］。在评价过程，通常都要涉及到对于指标权重的设定问题，然后以某种评价目标属性值及其权重的价值组合规则来输出评价结果，并进行排序，评价方法可分解为指标体系的确定与指标权重的确定两部分，赋权方法是评价方法的核心部分，应重点对该领域进行研究、归纳和分析［2］。

当前，用于指标权重赋值的方法有数十种之多，可以分为主观赋权法和客观赋权法两大类［3，4］，从中选取科学合理的赋权方法进行指标权重赋值具有十分重要的实践意义。因此，本文选用六种常用赋权方法，即德尔菲法、层次分析法、熵权法、主成分分析法、极差最大化法和均方差法，以湄潭县基本农田划定为例，通过研究不同赋权方法对同一指标体系评价结果的影响，试图从中选取一种最优的指标赋权方法。

1 指标体系的建立与标准化

1.1 评价指标体系的构建及评价单元的确定

基本农田是指按照一定时期的人口和社会经济发展对农产品的需求，依据土地利用总体规划确定的不得占用的耕地，是耕地的精华，是土地利用总体规划中的一个重要部分［5，6］。基本农田的数量和质量直接关系着我国的粮食安全问题［7］，科学合理划定基本农田对于保护耕地、稳定农业生产、确保粮食安全、保证生态安全、促进区域社会经济可持续发展起到关键作用。

基本农田不仅要具有高产能的特性，而且必须保证其长期、稳定的农业用途，产能的高低是由自然质量条件的好坏决定的，而其农业用途的长期性及稳定性取决于立地条件的好坏［8］。综合考虑耕地的自然条件和立地条件，依据农用地分等定级成果和土地利用现状调查成果选取农用地自然等、坡度值、交通条件、水利条件、与居民点距离和集中连片程度6 个因素建立湄潭县基本农田划定指标体系，如表1。

为确保数据可比性和统计资料的完整性，本文以土地利用类型和评价指标体系值作为划分评价单元的依据，将土地利用类型和指标值相同的图斑作为一个评价单元进行分析研究。

表1 湄潭县基本农田划定评价指标体系

1.2 评价指标数据标准化处理

从指标体系来分析，集中连片程度为正指标，即指标值越大越好的指标;而农用地自然等、坡度、交通条件、水利条件、与居民点距离为负指标，既指标值越小越好的指标。由于各指标的涵义不同、计算方法不同、量纲不同，因而难以进行比较，首先需要对指标进行标准化［6］。采用以下方法对评价体系原始数据进行标准化处理，其公式为:

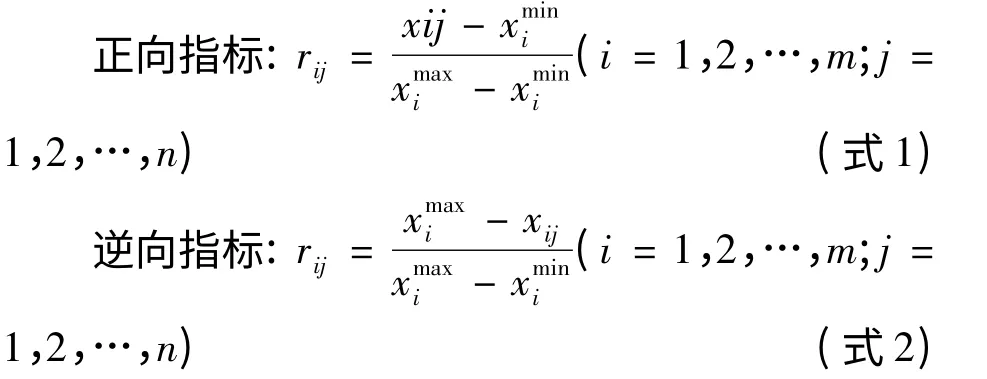
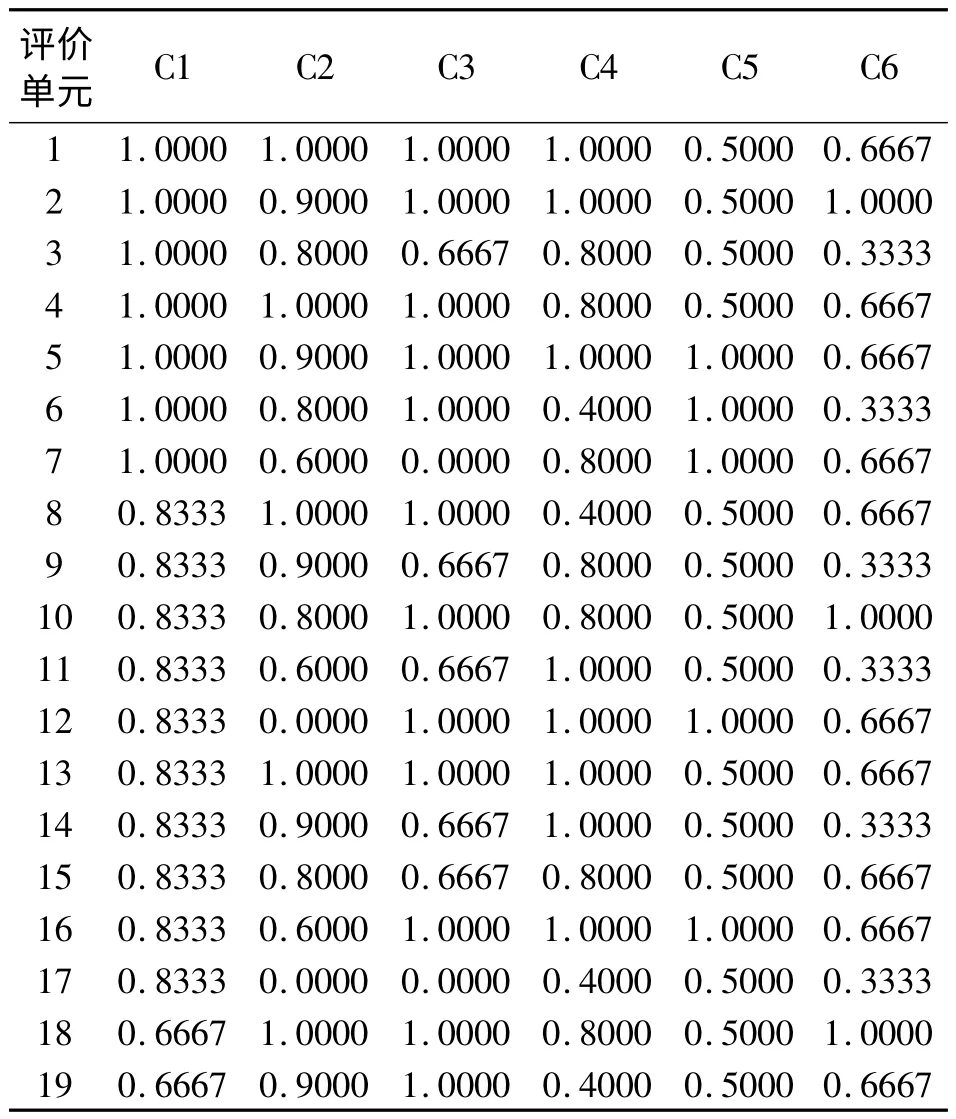
表2 湄潭县基本农田划定指标标准化数据

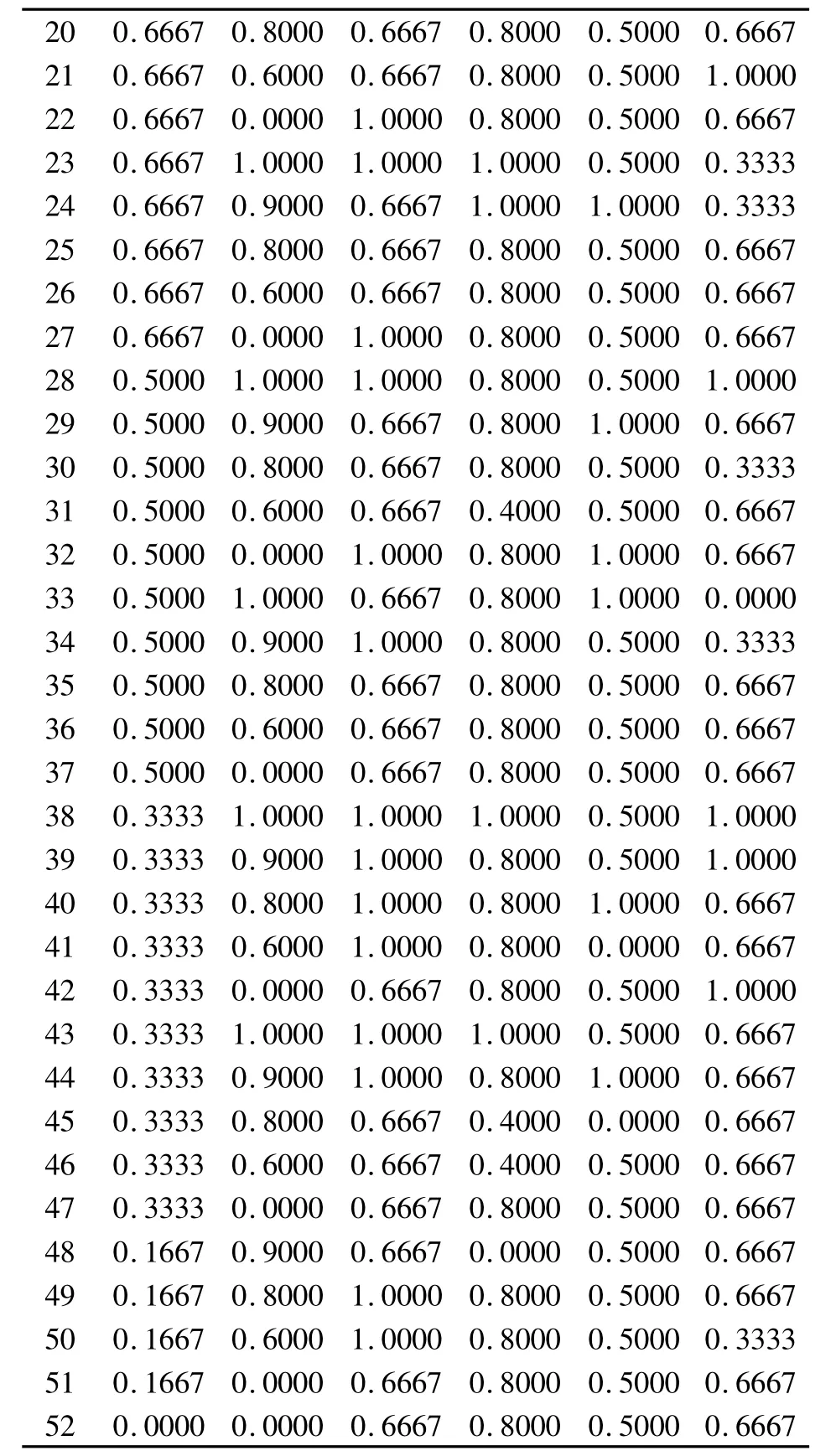
评价指标标准化数据结果的描述统计量见表3。从均值和标准差来看，指标C1、C2 均值较小、标准差较大，C3、C4 的均值较大、标准差较小。从指标偏度来看，C1、C2、C3、C4 和C6为负，说明分布是左偏态，此时数据低分值较少，中高分值较多;而C5 的偏度为正，说明分布是右偏态，此时数据高分值较少，中低分值较多。从指标峰度上看，除C1、C2 是平峰(分布形态比正态分布平坦)分布之外，其余全是尖峰(分布形态比正态分布陡峭)分布。

2 权重赋值

2.1 德尔菲法

特尔菲法(Delphi 法)［9］，又名专家打分法，是专家采用匿名发表意见的方式经过几轮征询使专家小组的预测意见趋于集中［10］。本文选择从事土地资源管理、土地利用规划、农业生产和管理等相关领域的专家进行咨询打分［11］。

表3 标准化数据描述统计量

表4 德尔菲法赋权结果

2.2 层次分析法

美国运筹学家、匹兹堡大学教授T.L.Saaty 于20 世界70 年代提出来的层次分析法(analytic hierarchy process，简称AHP)，是一种定性与定量相结合的决策分析方法［12，13］。本研究将评价指标体系划分为指标层和准则层，采用专家打分确定评价因子的相对重要性。

层次分析法使用方便，但主观性强。研究区应用层次分析法赋权结果如下表(表5)。

表5 层次分析法赋权结果

2.3 熵权法

嫡值法是一种根据各项指标观测值所提供的信息量的大小来确定指标权数的方法［14］。它根据各指标值的变异程度，通过分析数据之间的信息熵确定各指标的权重。首先，对评价体系设有n 个评价单元，m 个评价指标，得到指标矩阵Rij=(rij)mxn;其次，根据熵的定义，对于某个指标ri，有熵

表6 指标信息熵

最后，由指标信息熵计算熵权

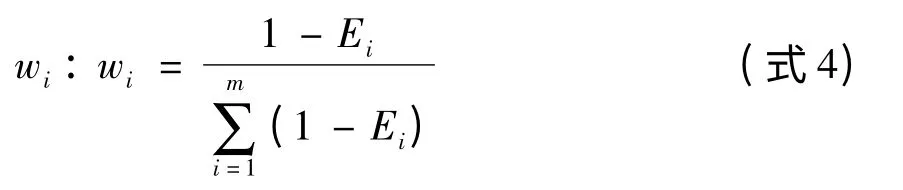
表7 熵权法赋权结果

2.4 主成分分析法

主成分分析是一种常用的多元统计方法，它把多个评价指标综合成n 个主成分，再以提取出的n个主成分的方差贡献率为权重值构造一个综合指标，并作出判断［18］。当原有的m 个评价指标的关联性较高时，能有效避免指标间信息的叠加，并且能根据指标所提供的信息，通过数学运算而主动赋权。计算所选变量的相关系数矩阵，并进行因子分析适宜性检验。其中，KMO=0.470 ＜0.6，表明该例不适合用主成分分析法赋权。根据下面的公式计算出权重［19］，计算所得权重如表8:

表8 主成分分析法赋权结果

2.5 极差最大化法

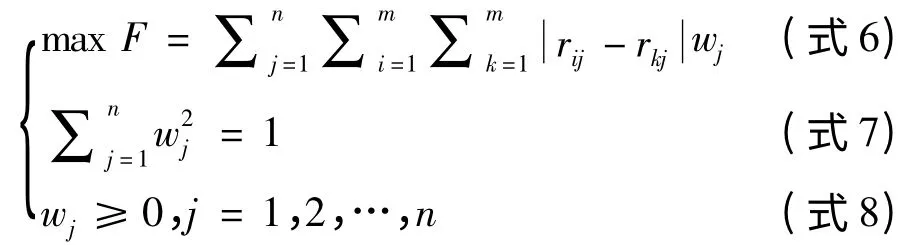
求解该优化模型，得出最优解w=(w1，w2，…，wn)，并将其归一化的结果作为各指标的权重系数。

表9 极差最大化法赋权结果

2.6 均方差法

均方差决策分析法的基本思路是，以各评价指标为随机变量，各评价对象在指标下的无量纲的属性值为该随机变量的取值，首先计算出这些随机变量的均方差，将这些均方差进行归一化处理，其结果即为个指标的权重系数［21］。

(1)将各评价指标作为随机变量，并求出这些随机变量Yj的平均值:

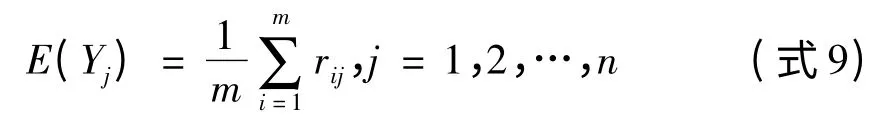
(2)求出指标 Yj的均方差:σ(Yj)=

(3)求出指标Yj的权系数:

表10 均方差法赋权结果

3 结果与分析

3.1 赋权结果分析

以湄潭县基本农田划定评价为例，分别采用以上6 种赋权方法对评价指标体系进行赋权，由以上结果可以看出，对同一评价指标采用不同的赋权方法所赋权重是不一样的。德尔菲法赋权结果:C1(0.398)＞C2(0.202)＞C3(0.114)＞C4(0.103)＞C5(0.096)＞C6(0.087);均方差法赋权结果:C2(0.387)＞C1 (0.175)＞C6 (0.145)＞C4(0.114)＞C5(0.103)＞C3(0.076);极差最大化法赋权结果:C2 (0.236)＞C1 (0.216)＞C6(0.173)＞C4(0.153)＞C5(0.135)＞C3(0.087);主成分分析法赋权结果:C4(0.313)＞C3(0.292)＞C6(0.199)＞C5(0.112)＞C1(0.051)＞C2(0.033);层次分析法赋权结果:C1(0.384)＞C2(0.172)＞C6(0.150)＞C4(0.104)＞C5(0.098)＞C3(0.092);熵权法赋权结果:C1(0.325)＞C6(0.194)＞C5(0.187)＞C2(0.118)＞C4(0.090)＞C3(0.086)。采用Spss 19.0 对不同方法的赋权结果进行相关性检验，结果见表11。

表11 6 种赋权结果相关系数矩阵

由以上相关系数矩阵表可看出，熵权法与除了主成分分析法之外的4 种赋权方法的相关性系数均大于0.6，其中与德尔菲法的相关性最好，相关系数达到了0.974，显著性水平为0.01。极差最大化法与除了主成分分析法、层次分析法之外的3 种方法结果的相关性系数在0.5 以上。德尔菲法与除了主成分分析法之外的4 种赋权方法结果的相关性系数也都在0.5 以上，其中与层次分析法的相关性最好，达到了0.991。均方差法与除了主成分分析法、层次分析法之外的3 种赋权方法结果的相关性系数在0.6 以上，其中与极差最大化法的相关性最好，相关系数为0.946。可见主成分分析法的赋权结果与其余5 种赋权方法的相关性较低、甚至呈现负相关，这也符合之前所做的KMO 检验和Bartlett 检验(KMO ＜0.6)，认为此例不适合用主成分分析法赋权，故不考虑此法。其他5 种方法的赋权结果的相关性，尤其是熵权法与德尔菲法、层次分析法和均方差法4 种方法之间的相关性可以看出，不同方法的赋权结果间存在着不同程度的一致性，同时也可看出德尔菲法与层次分析法这两种主观赋权方法的一致性。

综合以上可以看出，虽然不同赋权方法对同一评价体系的赋权结果不同，但是不同结果间的一致性也较为明显。可以进一步从不同赋权方法对指标数据离散化程度的敏感性方面来探讨，分析比较各种方法结果间的一致性，以期选择出一种最优的指标赋权方法。下面本文通过减少指标个数来探讨各种方法赋权结果的变化情况。

3.2 指标递减的赋权结果分析

在样本数据不变和指标个数减少的情况下，分析各指标数据间的差异性。指标减少是在全部指标体系的基础上依次删除指标C6、C5、C4、C3，在此基础上分别运用除主成分分析法的5 种赋权方法对减少指标体系进行赋权，赋权结果图1—图4所示:

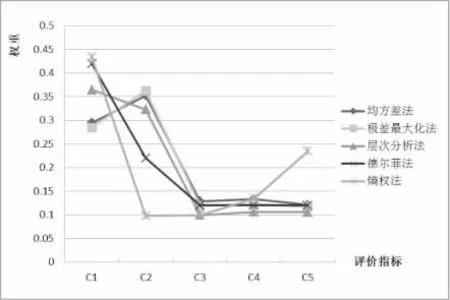
图1 五个指标

图2 四个指标

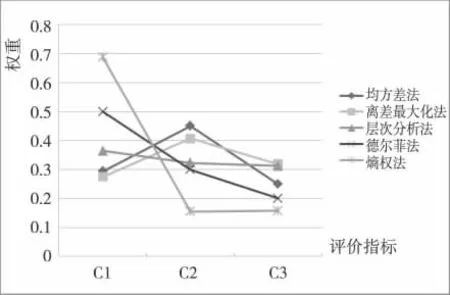
图3 三个指标

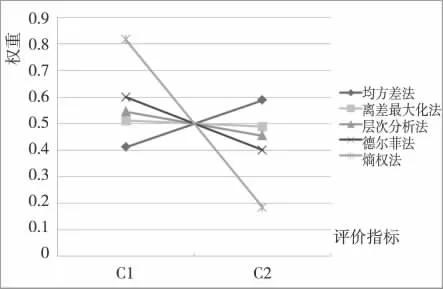
图4 两个指标

从上图可以明显看出，各种方法的赋权结果虽然不同，但是伴随着指标个数的减少，不同方法对评价指标的区分度显示出明显的一致性，尤其是只剩下两个指标时，各种方法对指标的区分度显而易见。随着指标个数的减少直至剩下两个指标时，熵权法始终能够明确区分各评价指标间的差异性;均方差法对指标区分也相对明显，但不如熵权法;德尔菲法和层次分析法这两种主观赋权法对指标的区分度大体一致，但随着指标个数的减少，对指标的区分度已经不那么明显了;离差最大化法对指标的区分度也随着指标个数的减少而降低。

4 结论

综上所述，本研究对湄潭县基本农田划定数据运用6 种不同赋权方法的赋权结果进行了比较分析，结果表明:主成分分析法的使用有着严格的限制条件，要求评价指标之间具有较高的相关性;熵权法具有区分指标差异的优越性，确定为最优。因此，当不同方法区分各评价指标间差异性不大时，即不同方法的赋权结果相近时，可任意选取一种赋权方法;但当不同方法对指标差异的区分度相差大时，应选用区分度大的赋权方法。

［1］唐平英，黄丽霞.基于GIS 的永久性基本农田划定－以中方县为例［J］.长沙理工大学学报，2013，10(1):61－67.

［2］何小勇.铁路物流系统评价指标权重确定方法研究［D］.重庆工商大学，2010.

［3］李亮.评价中权系数理论与方法比较［D］.上海交通大学，2009.

［4］王书吉.大型灌区节水改造项目综合后评价指标权重确定及评价方法研究［D］.西安理工大学，2009.

［5］法律出版社法规中心.中华人民共和国土地管理法［M］.北京:法律出版社，2007.

［6］张丹丹，张安明，张引，等.基于GIS 技术的基本农田划定研究［J］.中国农业资源与区划，2012，33(6):51－56.

［7］李晓倩.土地资源评价指标权重赋值方法的比较研究－以庄浪县农村居民点整理潜力评价为例［D］.甘肃农业大学，2012.

［8］董秀茹，尤明英，王秋兵.基于土地评价的基本农田划定方法［J］.农业工程学报，2011，27(4):336－339.

［9］于勇，周大迈，王红，等.土地资源评价方法及评价因素权重的确定探析［J］.中国生态农业学报，2006(4):213－215.

［10］王晓燕，田永中，高凡，等.基于GIS 的永久性基本农田划定技术方法探讨［J］.西南大学学报:自然科学版，2013，38(3):127－133.

［11］镇常青.多目标决策中的权重调查确定方法［J］.系统工程理论与实践，1987，7(2):16－24.

［12］刘占伟，邓四二，滕弘飞.复杂工程系统设计方案评价方法综述［J］.系统工程与电子技术，2003，25(12):1488－1491.