高中数学“导数”教学问题探究

罗娅+汤强

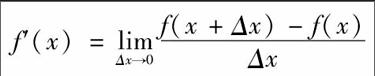
摘要：随着新课程标准的改革，导数作为新的知识出现在高中数学教材中，导数的研究，进一步的为解决了求函数的零点，复合函数单调性，以及不等式的证明等方面的问题提供了简洁的方法。但在中学教学过程中却存在三种典型的“偏见”，而如果教学中回避这些“偏见”，会导致我们不能正确定位高考考点，使学生对导数概念模糊不清，教师如何高效的处理好这些“隐患”把导数这一教学板块教学好，是值得的我们商确和反思的。

关键词：导数;教学;问题

中图分类号：G635文献标志码：A文章编号：2095-9214（2015）10-0057-02

导数是高中数学的重点之一，也是历年高考数学试题命制的热点和重点，题型变化灵活，能考察学生数形结合、分类讨论的能力。除了传统的求单调性、最值外，还增加开放性、探究性问题等;所以学习好导数是非常有必要的，然而教学中却存在了一下几点教学偏见。

1.偏见之一：忽略函数极限的内容直接讲导数定义

极限这个词汇来源于数学微积分，极限是微积分中的基础概念，它指的是变量在一定的变化过程中，从总的来说逐渐稳定的这样一种变化趋势以及所趋向的值（极限值）。高中教材中所体现的极限思想即有数列极限和函数极限两种，虽然说极限这个数学概念实在大学中进一步深入研究探讨的，但是在研究导函数概念的由来就必须要初步的掌握极限的相关知识，例如在导函数公式中

f′（x）=limΔx→0f（x+Δx）-f（x）Δx

就存在无限趋近的概念，变量无限趋近于0，这种数值逼近也是极限思想的一种体现。而在学习导数定义时，是将我们的平均速度近似看做瞬时速度，也是一种极限思想，因此在导数新课的讲解中，不能忽视不讲极限，跳过极限而给学生讲导数，而是应该让学生了解到极限的存在，以及讲解简化极限的知识内容，让学生自身感悟极限的思想和过程，为大学深入学习微积分打下基础。高考中也存在极限的考法：

比如下例：

例1（2011年四川卷理科5题）

limx→x0f（x）存在是函数f（x）在点x=x0连续的（）

A.充分而不必要条件B.必要而不充分条件

C.充要条件D.既不充分也不必要条件

分析：理论基础：（高等数学）

函数在某点连续，满足条件：

（1）函数在此点有定义;

（2）函数在此点的左右极限相等;

（3）函数在此点的极限值和函数值相等。

所以说极限存在的前提是要满足以下三点，上述问题表述的易得到答案（B）。

2.偏见之二：过分重视教材实例，忽视指导观察函数本质

在新课改之前的数学教学过程中，教师教导导函数一般就是直接给学生陈诉概念，让学生记忆概念内容，并没有阐述导函数概念的由来，新课改后，教学强调理论联系实际，体现数学其实从生活中提取出来的数学模型，为了更加贴切生活，教材中确实呈现了多种与导函数由来的生活实例与背景，在导函数开篇，就以一道关于气球膨胀求瞬时速率的问题，接着所有的例子基本都是与生活挂钩的，比如说求浓度，温度，变量的速率，直观的体现了新课改的特点，可是这样真的能让学生很好的掌握了导函数的本质么？

其实例子是可以举，但是不能强把所有的只要有求变量速率的东西都往导函数靠拢，要抓导函数的本质，其实实例中所呈现出来本质上也是一种函数，可能这些函数是我们的基本初等函数，有些则是抽象函数，但解决的方法往往是抓住变量与变量之间的改变而得到的结果，譬如教师举了太多实例的东西，如果这时候，我们举出一道求“函数y=x2从到的平均变化率”，难道学生还要把它转化为实际问题来做这道题？解决这道题关键是抓住自变量的改变和自变量改变引起的函数值的改变，从而得到结果，所以教师在讲解过程中，不能太重实例，要透过现象看本质，不管是实例还是非实例，都是要通过指导学生观察发现函数模型，函数模型抓到了，解决起来就容易的多。

例2：一杯80℃的热红茶置于20℃的房间里，它的温度会逐渐下降，温度T（单位：℃）与时间t（单位：min）间的关系，由函数T=f（x）表示。

（1）f（t）的含义是什么？f（t）的符号是什么？为什么？

（2）F（3）=-4的实际意义是什么？如果f（3）=60（℃），你能画出函数在点t=3时图象的大致形状吗？

解析：

（1）f（t）的含义表示“瞬时温度”，红茶温度在下降，f（t）的符号是负号，f（t）<0.

（2）F（3）=-4表明在3℃附近时，红茶的温度约以4℃）/min的速度下降。

T=f（t）在点（3，60）处的切线斜率K=-4.

T=f（t）在t=3时的图象的大致形状如图所示。

3.偏见之三：“止”于教材学导数

由于近几年高考题中参照了教科书中的习题例题来出题，所以我们更要重视教材这一观念本身没错，但是“止”于教材学导数，就大大违背了这一观念，这并不是要求我们只把教材上的内容处理好就可以了，高考题考察的是导函数概念的本质，如果我们把本质东西弄懂了，那么即使不是一样的数据的题型，我们依然会可以轻松的解决问题。

例3.（2013年高考广东文科卷第21题）

设f（x）=x3-kx2+x（k∈R）

（1）当k=1时，求函数f（x）的单调区间;（2）当k<0时，求函数f（x）在[k，-k]上的最小值m和最大值M。

教材原型（人教A版高中数学教材选修2-2第26页练习1（4））

判断函数f（x）=x3-x2-x的单调性，并求出单调区间。

演变过程高考题是上述教材原型题的改编题，将二次项系数-1改为参变量-k，一次项系数-1改为+1.高考真题2的第（Ⅰ）问，实质上就是教材习题中的求函数的单调区间，第（Ⅱ）问是在第（Ⅰ）问的基础上增加对参数的讨论，求三次函数在给定区间上的最值问题，需要我们熟练掌握含参数讨论求最值问题.endprint

从以上的分析中我们可以看出，教材在高考复习中占据着不可替代的地位.教材的例题和习题蕴含着丰富的知识点、数学思想方法和解题技巧.我们若能对一些典型的例题、习题进行认真的深究，在高三复习中合理地再利用，挖掘其内在的潜能，探求到更一般的结论，做到知识点、思想方法源于教材却又高于教材，如此不仅能提高解决似曾相识的问题的速度和能力，也有利于提高高考复习的质量。

4.教学建议

针对以上出现的三个教材中常见的偏见，我将制定以下教学方案：

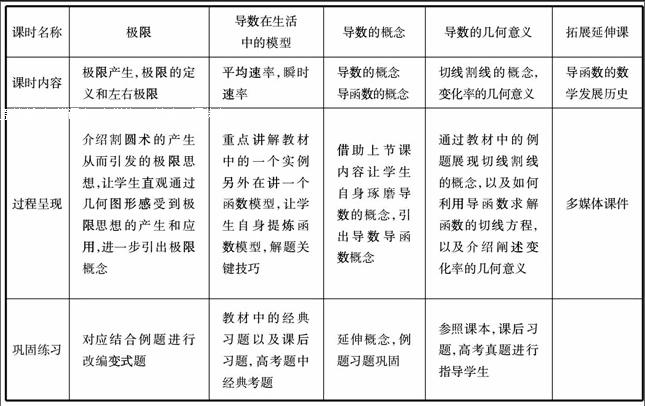
课时名称极限导数在生活

中的模型导数的概念导数的几何意义拓展延伸课

课时内容极限产生，极限的定义和左右极限平均速率，瞬时速率导数的概念

导函数的概念切线割线的概念，变化率的几何意义导函数的数学发展历史

过程呈现介绍割圆术的产生从而引发的极限思想，让学生直观通过几何图形感受到极限思想的产生和应用，进一步引出极限概念重点讲解教材中的一个实例另外在讲一个函数模型，让学生自身提炼函数模型，解题关键技巧借助上节课内容让学生自身琢磨导数的概念，引出导数导函数概念通过教材中的例题展现切线割线的概念，以及如何利用导函数求解函数的切线方程，以及介绍阐述变化率的几何意义多媒体课件

巩固练习对应结合例题进行改编变式题教材中的经典习题以及课后习题，高考题中经典考题延伸概念，例题习题巩固参照课本，课后习题，高考真题进行指导学生

事实上，讲好第2和第3课时是讲好导函数这节内容的观念，要求教师重点把握这两节的处理对教师本身对教材的理解有一定的难度和挑战性，这对今后教学，备考的启示与建议：

（1）在研究函数单调性的方法上，我们学过两种解决函数单调性方法，一是定义法，另一种是求函数导函数求解，但是运用求导数法一般比用单调性定义等常规方法简单易行，我们需要在面对不一样的题型面前选择适合的方式进行求解，常见的基本初等函数直接用定义法即可解决，针对复合函数，最好利用导函数解决更加简单易行，要注意的是不管用那种方法求解，都要注意函数定义域的取值范围这个是许多学生出错的地方。

（2）建议新教材毕竟把平面向量提前，不等式一章也可适当前置，为系统学习函数理论做好必要的铺垫。高三总复习时，可适当调整顺序，如把导函数归为函数一类进行复习。有效的掌握函数的性质，最值单调性等

（3）对于极限这种新知识点，大致讲讲即可，切勿深入研究。

（作者单位：西华师范大学）

参考文献：

[1]课程教材研究所.面向21世纪中小学教材建设现代化研究与实践[M].北京：人民教育出版社，2003：7

[2]人民教育出版社课程教材研究所等编著.普通高中数学课程标准实验教科书（选修2-2，2-1）[M].北京：人民教育出版社，2007.

[3]波利亚著：《怎样解题》，科学出版社

[4]波利亚著：《数学的发现对解题的理解，研究和讲授》，科学出版社endprint