“平行四边形面积”一课教学的探讨

2015-11-21江苏南通师范学校第一附属小学226001

小学教学参考 2015年5期

关键词：多边形长方形平行四边形

江苏南通师范学校第一附属小学（226001）季勇

“平行四边形面积”一课教学的探讨

江苏南通师范学校第一附属小学（226001）季勇

“平行四边形面积”既是小学数学教学的重点课程内容之一，又是后面学习三角形、梯形等多边形面积的关键性基础知识，对多边形面积公式的演算过程具有重要意义。通过对“平行四边形面积”教学的探究，以期获得合理、有效的教学方法，使学生得到真正的发展。

小学数学平行四边形面积教学方法

“平行四边形面积”是小学数学五年级的教学内容，归属多边形面积的课程教学板块。无论从课程知识目标、教学方法目标，还是从情感认知与价值观目标的角度来看，“平行四边形面积”无不体现出其计算方法的重要性，对培养学生的分析归纳能力、引导学生感悟逻辑推演过程具有重大作用。同时，“平行四边形面积”既是小学数学教学的重点课程内容之一，又是后面学习三角形、梯形等多边形面积的关键性基础知识，对多边形面积公式的演算过程具有重要意义。因此，教师要充分重视“平行四边形面积”教学的研究，才更能使学生对此类教学内容产生浓厚的学习兴趣。下面，笔者以平行四边形面积的计算为探究对象，谈谈个人的教学和体会。

一、从现实事物的转变中感悟平行四边形面积的教学方法

在学习平行四边形面积的计算之前，学生已经学过长方形面积的计算方法及公式。因此，课堂教学中，教师要有意识地引导学生把长方形（或正方形）面积的推演过程转变到平行四边形上来，使他们从中感知平行四边形面积的推演方法，再进行面积计算方法的探讨。教师也可以引导学生运用分割法探究平行四边形面积的计算，即将平行四边形放在方格纸片上临摹后，数出其所占的方格个数来大概计算平行四边形的面积，此方法在现实生活中可以很方便地计算出一个不规则多边形的面积。以上两种计算平行四边形面积的方法都有一个相同点，那就是将平行四边形转变为1个或n个长方形（或正方形）。这种转变的方法一般有两种考虑：一是看得见的，即上述两种方法中，教师都向学生展示了方法的名称，并简单说明了其使用的条件，重点培养学生在现实生活中能够感知所学知识的能力；二是看不见的，即上述两种方法中，教师不给学生展示方法的名称，重在说明方法的应用，让学生发挥其主观能动性，自己动手推演、感知这种转变方法的使用条件，培养学生感悟知识的潜意识。

二、引导学生从平行四边形面积推演过程中理解其计算方法

课堂教学中，教师可以在长方形（或正方形）转变成平行四边形的基础上，引导学生进一步探究平行四边形面积计算的推演过程。首先，教师画出长方形（或正方形）和平行四边形让学生对比，并提出需要探讨的问题：“怎样计算平行四边形的面积？”其次，引导学生利用工具推演由长方形（或正方形）转变成平行四边形的过程。值得关注的是，此推演过程应重复向学生展示，通过多次重复的推演，使学生的脑海里出现不同的但边长相同的平行四边形。这样教学的目的，在于使学生感知不同的夹角但边长相同的多个平行四边形（如图1和图2）。教师通过展示平行四边形的不同转变，引导学生进行仔细的对比、思考，学生就容易联想到原来是平行四边形相邻两边之间的夹角发生了改变，才使得平行四边形的高随之改变，从而导致平行四边形的面积发生改变。同时，学生还可以进一步推演，得出引起平行四边形面积发生变化是因其的高起到了主要影响作用。

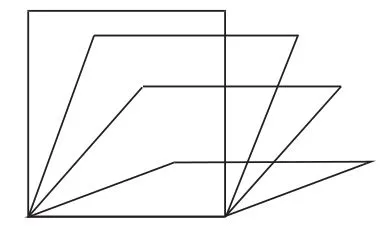
图2

最后，教师引导学生用平行四边形的转变过程来推演其面积的计算公式，并提出问题：“在联想到平行四边形面积可能与之对应的边长和高度相关后，又怎样来进行验证呢？”学生通过问题的探究，很容易发现用平行四边形的两个顶点来画平行对边的高，如此就形成了一个矩形和两个三角形，再证明两个三角形为全等三角形，这样就完全转变成一个矩形的面积来计算了，顺其自然地得出平行四边形面积的计算公式为底边×高，使其推演过程合情合理。