TbFeCo薄膜激光诱导超快自旋动力学的成分比研究

陆一帆，姜建伟，张晓磊，楼柿涛，金庆原

（华东师范大学 精密光谱科学与技术国家重点实验室，上海 200062）

当今社会已进入信息技术时代，数字存储领域作为信息技术的重要组成部分，受到了国内外研究者们的广泛关注.磁存储技术作为现代信息存储的基本方式，从出现到现在不断提高记录密度与速度以适应信息技术的快速发展.随着激光技术的不断进步，激光辅助磁存储技术成为实现大容量和高速度存储器的新技术［1］.磁性材料的超快自旋动力学研究是当前人们研制高速磁存储器的必要条件.目前研究磁性材料超快自旋动力学的手段主要是时间分辨的磁光克尔效应与铁磁共振等方法.

20世纪80年代，国外各研究小组利用时间分辨的磁光克尔效应测量方法相继发现简单铁磁材料的超快退磁现象［2－3］.1996年，Beaurepaire等研究者采用60fs脉宽的激光脉冲，对镍薄膜进行了时间分辨磁光克尔谱的测量，观察到260fs左右的超快退磁现象，并建立三温度模型，采用电子、自旋和晶格系统的能量转换过程来解释此现象［4］.近年来，三温度模型解释超快退磁现象被广泛认同，并用于解释各种新型磁性材料的超快自旋动力学过程［5－6］.

Kimel的小组做过稀土－过渡金属（RE－TM）材料GdCoFe的变泵浦功率实验［7］，观测到GdFeCo中存在类似两步退磁，并提出四温度模型［8］解释此现象.然而在RE－TM 材料中，稀土原子和过渡金属原子具有相反的磁矩方向，当稀土元素与过渡金属元素的成分比在某一特定值或材料在某一特定温度下时，两者的磁矩大小相等方向相反，互相抵消，整体不体现磁性.这种特性被称为磁性补偿点特性，是适用于激光辅助磁存储技术的重要前提［9］.磁性补偿点对于RE－TM 材料中电子、自旋和晶格相互作用的影响是该材料超快动力学的重要方面.到目前为止，关于不同成分比的RE－TM 材料对其超快自旋动力学过程的影响还不明确.本文选择不同成分比的RE－TM 材料TbFeCo磁性薄膜进行时间分辨磁光克尔效应测量，观察成分比对于材料中磁矩的退磁－弛豫现象的影响，推测材料中电子、自旋和晶格的超快动力学过程.

1 实 验

1.1 实验装置

本实验采用基于磁光克尔效应的泵浦－探测技术来观测TbFeCo磁性薄膜的时间分辨磁光克尔谱，从而研究其激光诱导超快自旋动力学过程.磁光克尔效应简单理解即为具有线偏振特性的激光入射到具有磁矩（包括感应磁矩）的介质表面上，其反射光的偏振方向发生旋转，其旋转角度大小与样品磁性成正比［10］.

图1 实验装置图Fig.1 Schematic diagram of the experiment setup

本实验采用的激光束中心波长为800nm，脉宽约为100fs，重复频率为1kHz.实验光路及装置如图1所示.飞秒脉冲激光束经过分束镜分成泵浦和探测两束光.泵浦光经高精度步进电机组成的延迟线、斩波器、聚焦透镜等入射到样品表面，探测光经起偏器、聚焦透镜等入射到样品表面同一位置.为确保泵浦光与探测光的重合度，泵浦光光斑略大于探测光.探测光反射光通过整形光阑、聚焦透镜、检偏器等，由光电探测器收集，经由锁相放大器及数据采集卡传输到电脑端的控制程序中.时间分辨通过控制步进电机实现，最小时间分辨率为6.6fs.

1.2 实验样品

本实验的TbFeCo磁性薄膜采用美国Kurt J.Lesker公司生产的高真空磁控溅射仪制备，生长于康宁玻璃衬底之上.实验中Tb与FeCo的不同成分比是通过保持FeCo的制备条件不变，改变Tb 的溅射功率来实现.样品结构为glass／Ta（1.5）／Tbx（Fe34Co66）1－x（12.0）／Ta（3.0），单位为nm，其中x＝11%，14%，17%，20%，23%.本实验制备的TbFeCo磁性薄膜属于非晶薄膜，具有较高的垂直磁各向异性和良好的垂直磁记录应用前景［11］.另外该系列样品具有较大的磁光克尔角度，易于实验测量.

样品的静态磁性由振动磁强计（VSM）测量，可进行磁滞回线的研究.由于TbFeCo是一种亚铁磁性非晶态合金，具有磁性补偿点，如图2 所示的垂直于膜面方向的M－H 曲线，当x＝23%时，样品净磁矩接近于零，M－H 曲线表现出无明显的磁滞翻转，x＜23%时，FeCo的磁矩占主导，各成分下的样品均表现出垂直磁各向异性，磁滞回线表现出良好的矩形度.需要指出的是，x＝23%时，M－H 曲线无明显的磁滞翻转还可能是因为所加外磁场小于其矫顽场，而在磁性补偿点附近的样品通常都拥有相对很大的矫顽场，因此，可以判定此系列样品的磁性补偿点在x＝23%附近.本文中我们主要集中研究Tb含量较小（贫Tb）情况下TbFeCo磁性薄膜的自旋动力学特性.

图2 Tbx（Fe34Co66）1－x的极向磁滞回线（x＝14%，23%）Fig.2 Polar magnetic hysteresis loop of Tbx（Fe34Co66）1－x（x＝14%，23%）

2 结果与讨论

图3为Tb含量较小（贫Tb）时的短程时间分辨磁光克尔谱.各样品均存在450fs左右的超快退磁现象，此过程与其他材料类似［12－14］.如图所示，随着Tb含量增加，超快退磁幅度减小，该现象主要由于不同成分样品的净磁矩随着Tb含量逐渐增多而降低，故磁光信号呈现出逐渐减弱趋势.与其他实验结果相比不同之处在延迟时间1.5ps后，由图3可以发现Tb功率为11%、14%和17%的样品出现了第二步退磁.

为了观察第二步退磁的全过程，我们测量了延迟时间达到200ps的长程时间分辨磁光克尔谱，如图4所示.其中，第一步退磁由于是亚皮秒级别，故看起来只有一个向下的峰.从图4中可以清晰地看出，第二步退磁时间约在30ps左右，而且随着Tb含量增加，第二步退磁幅度减小.

图3 Tbx（Fe34Co66）1－x的短程时间分辨磁光克尔谱（x＝11%，14%，17%，20%）Fig.3 The short－term time dependence magnetooptical Kerr spectra of Tbx（Fe34Co66）1－x（x＝11%，14%，17%，20%）

图4 Tbx（Fe34Co66）1－x的长程时间分辨磁光克尔谱（x＝11%，14%，17%，20%）Fig.4 The long－term time dependence magnetooptical Kerr spectra of Tbx（Fe34Co66）1－x（x＝11%，14%，17%，20%）

常用的三温度模型已不能解释两步退磁现象，我们尝试利用相关文献中的四温度模型来解释［8］.在TbFeCo这类RE－TM 合金材料中，温度系统有4个，分别为RE 原子Tb自旋系统、TM 原子FeCo自旋系统（Fe和Co特性相近，故可以把Fe和Co看成一个自旋体系）、电子系统与晶格系统.各系统之间的相互作用可以用以下公式计算［8］：

其中C 为比热，G 为耦合常数，小标中e，l，s分别代表电子、晶格、自旋.表示Tb自旋系统与FeCo自旋系统之间的耦合.

在泵浦光入射到样品表面，激发样品后，电子系统接收光子能量从而温度迅速升高，随后电子系统通过光电子将能量传递给Tb与FeCo自旋系统，造成FeCo自旋系统亚皮秒的自旋温度上升，因为自旋系统温度上升会导致磁矩排列的无序化，即与磁性成反比，故在磁光克尔信号上形成了0～500fs之间的急剧下降.而Tb原子由于磁性来源于4f电子，其波函数在原子核附近，很少与邻近电子的波函数重叠，必须借助5d～6s传导电子进行间接交换，其上升速度相较FeCo自旋系统慢很多，最大退磁时间在35ps左右（见图4）.公式（3）中－）一项因此为负值，从而导致FeCo自旋系统向Tb自旋系统传递能量.作为结果，FeCo自旋系统温度会在亚皮秒级别的迅速上升后开始下降，体现在磁光克尔信号上即为500fs左右的第一步退磁最低点.同时，晶格系统因为电子－晶格与自旋－晶格的相互作用，温度也在上升.当FeCo自旋系统温度由于FeCo自旋－Tb自旋作用下降至低于晶格系统温度时，晶格系统开始向FeCo自旋系统传递能量，故而FeCo自旋系统在减小后再度上升，在磁光克尔信号上形成了2ps左右的一个拐点.随后FeCo与Tb自旋系统温度会一起慢慢上升直至四温度系统均达到平衡状态，在磁光克尔信号上即为2ps至35ps之间的第二步退磁.35ps后，处于平衡态的各系统一起弛豫恢复至初始状态，即磁光克尔信号中35ps的第二步退磁最低点之后的过程.

图5为Kimel小组在GdCoFe体系中运用四温度模型得到的温度时间关系图［8］，从中可以看到，两步退磁现象符合四温度模型，因为Tb与Gd以及样品成分比的不同，图5中Gd系统达到平衡状态的时间在200ps左右.

另一方面，第二步退磁的时间比铁磁材料的超快退磁时间大两个数量级以及第二步退磁幅度均随着Tb含量增大而逐渐减小，这也可以用四温度模型唯象解释.在四温度模型中，退磁时间决定于各温度体系达到平衡状态的快慢，根据前述原因，TbFeCo样品中Tb自旋系统的温度变化远远慢于铁磁系统，故退磁时间比铁磁材料大数个数量级.另外，在TbFeCo样品中，Tb磁矩与FeCo磁矩方向相反，在贫Tb含量下，FeCo磁矩占主导，样品宏观净磁矩方向跟随FeCo磁矩，大小为FeCo磁矩与Tb磁矩的差值，而Tb含量逐渐增大意味着样品逐渐接近磁性补偿点，宏观净磁矩随着Tb含量增大逐渐减小，因此探测到的磁光克尔信号幅度也逐渐减弱，这个原因与图3中第一步退磁幅度的变化一样.作为佐证，我们测量了Tbx（Fe34Co66）1－x，x＝23%的样品，由于其Tb含量在磁性补偿点附近，我们没有看到任何退磁现象.

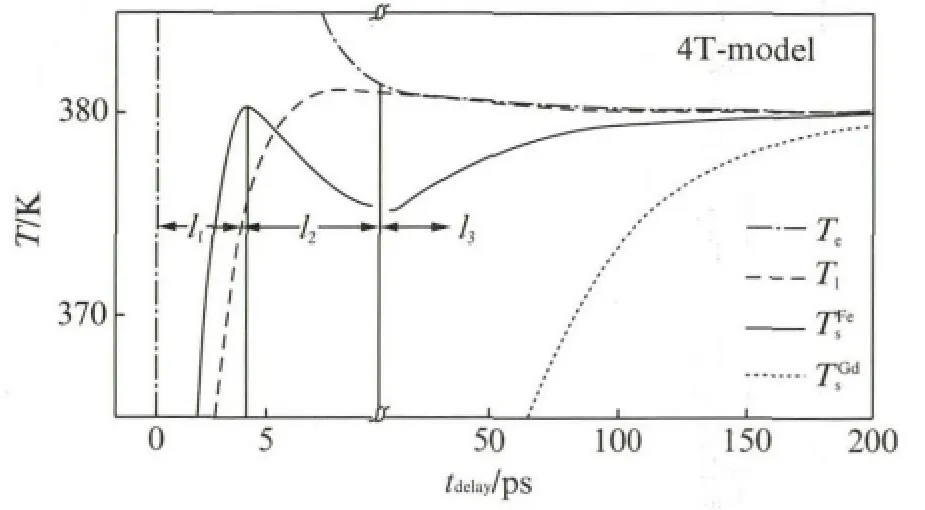
图5 四温度模型中GdCoFe各系统温度和时间关系曲线［8］Fig.5 The temporal evolution of the heat－reservoir temperatures in GdCoFe within the 4T model

图6 第二步退磁时间与Tb含量的关系曲线Fig.6 The second demagnetization time dependence on the composition ratio of Tb

进一步研究图4，我们将第二步退磁达到最低点的时间定义为t2，并对各成分比样品的t2进行整理统计，如图6 所示.从图中可以看出，第二步退磁时间随Tb 含量增大而增大，从Tb 含量为11%时的32.67ps增大到Tb含量为17%时的40.67ps.根据四温度模型，Tb含量增大，FeCo含量相对减小，Tb自旋系统中与FeCo自旋系统耦合的Tb原子数比例变小，其自旋系统温度上升相对就变慢，第二步退磁时间变长.从图4中还可以看出Tb含量为20%的样品未出现第二步退磁，一方面这可能源于样品含量靠近磁性补偿点，宏观磁性较弱，其第二步退磁幅度小于实验装置分辨率.另一方面，根据图4的解释，Tb含量可能存在临界点，超过这一临界点时，由于Tb原子数很多，其4f局域电子变得更不易通过5d～6s传导电子与FeCo的3d巡游电子进行能量交换以及更难与电子系统进行能量交换，因此Tb自旋系统温度不会发生剧烈变化或者说在百皮秒量级未体现出变化.

本文采用基于磁光克尔效应的泵浦－探测技术，成功探测到不同成分比的TbFeCo磁性薄膜的激光诱导超快自旋动力学过程.在实验中观测到百飞秒级别的超快退磁现象以及几十皮秒的第二步退磁现象.利用四温度模型合理解释两步退磁的原因，并分析了电子－自旋作用引起的第一步超快退磁机制以及晶格－FeCo自旋－Tb自旋作用引起的第二步慢退磁机制.不同成分比样品的实验结果对比，进一步佐证了四温度模型解释的合理性.

［1］Pan L，Bogy D B.Data storage：Heat－assisted magneticrecording［J］.Nature Photonics，2009，3（4）：189.

［2］Vaterlaus A，Beutler T，Meier F.Spin－lattice relaxation time of ferromagnetic gadolinium determined with time－resolved spin－polarized photoemission［J］.Phys Rev Lett，1991，67（23）：3314－3317.

［3］Vaterlaus A，Beutler T，Guarisco D，et al.Spin－lattice relaxation in ferromagnets studied by timeresolved spin－polarized photoemission［J］.Phys Rev B，1992，46（9）：5280.

［4］Beaurepaire E，Merle J C，Daunois A，et al.Ultrafast spin dynamics in ferromagnetic nickel［J］.Phys Rev Lett，1996，76（22）：4250－4253.

［5］Li Z，Yue S，Chen J J，et al.Ultrafast spatiotemporal relaxation dynamics of excited electrons in a metal nanostructure detected by femtosecond－SNOM［J］.Optics Express，2010，18（13）：14233－14237.

［6］Shih H C，Chen L Y，Luo C W，et al.Ultrafast thermoelastic dynamics of HoMnO3single crystal derived from femtosecond optical pump－probe spectroscopy［J］.New Journal of Physics，2011，13（5）：053003.

［7］Stanciu C D，Tsukamoto A，Kimel A V，et al.Subpicosecond magnetization reversal across ferromagnetic compensation points［J］.Phy Rev Lett，2007，99（21）：217204.

［8］Mekonnen A，Khorsand A R，Cormier M，et al.Role of the inter－sublattice exchange coupling in shortlaser－pulse－induced demagnetization dynamics of GdCo and GdCoFe alloys［J］.Phys Rev B，2013，87（18）：180406.

［9］Jiang X，Gao L，Sun J Z，et al.Temperature Dependence of Current－Induced Magnetization Switching in Spin Valves with a Ferrimagnetic CoGd Free Layer［J］.Phys Rev Lett，2006，97（21）：217202.

［10］顾培培，马 斌，张宗芝，等.一种新型大场纵向表面磁光克尔效应测量系统［J］.复旦学报：自然科学版，2009，48（4）：485－492.

［11］徐初东，翁嘉文，谭穗研.TbFeCo磁光薄膜飞秒激光感应超快磁化动力学研究［J］.材料导报B：研究篇，2014，28（1）：18－20.

［12］Scholl A，Baumgarten L，Jacquemin R，et al.Ultrafast spin dynamics of ferromagnetic thin films observed by femtosecond spin－resolved two photon photemission［J］.Phys Rev Lett，1997，79（25）：5146－5149.

［13］Ju G，Vertikov A，Nurmikko A V，et al.Ultrafast nonequilibrium spin dynamics in a ferromagnetic thin film［J］.Phys Rev B，1998，57（2）：R700－R703.

［14］Kise T，Ogasawara T，Ashida M，et al.Ultrafast spin dynamics and critical behavior in half－metallic ferromagnet：Sr2FeMoO6［J］.Phys Rev Lett，2000，85（9）：1986－1989.