集中式光伏电站的可靠性评价方法

胡文杰，孙耀杰，林燕丹，张军军

（1.复旦大学 光源与照明工程系，上海 200433；2.中国电力科学研究院，南京 210003）

随着节能减排、可持续发展等要求对传统能源的限制，可再生能源如风能、太阳能、潮汐能等，已经变得越来越重要.光伏发电是继风力发电之后，发展最迅速且成功应用的一种可再生能源.2014年，中国国家能源局拟定新增并网光伏发电项目14GW 的目标；2015年，全国拟定新增光伏并网发电项目15GW左右，其中集中式光伏电站8GW，分布式光伏电站7GW［1］.光伏电站的初始投入成本大，提高光伏电站运行期间的稳定性，控制运维成本，可以有效减少平均发电成本，这是光伏产业发展的核心.因此，建立光伏电站的可靠性评价模型，对光伏产业的稳定快速发展，显得非常重要.

针对光伏发电系统的可靠性分析，是目前光伏能源技术大规模发展急需解决的技术难题.国内的相关研究还较少，而国外的太阳能研究机构近几年正加大相关的研究投入.目前对光伏发电系统的可靠性模型主要分为基于元件故障的可靠性模型和基于资源限制的可靠性模型这2大类［2－4］.具体的分析方法有：蒙特卡洛模拟法、马尔科夫过程分析法、可靠性方块图法、故障树分析法.蒙特卡洛法是常用的模拟方法，可用于光伏发电系统的可靠性分析［5－6］，其计算较复杂，更加适合高度复杂的系统，如用蒙特卡洛法对光伏－风力混合发电系统进行可靠性评估［7－8］.马尔科夫过程分析法，将光伏系统的随机行为看作马尔科夫过程，并用空间状态图来描述［9－10］.由于马尔科夫回报模型受维数计算的限制，只限于低维数的空间状态运算.可靠性框图法，指基于方块图的方法建立光伏电站可靠性和运行性能的模型［11］，主要由失效模式及其影响的分析模块，寿命加速测试模块，系统可靠性／可用性建模模块这3部分组成.然而，失效模式的分析模块是建立在归纳分析的基础上，需要详细了解每一种故障模式后才能形成比较完善的功能模块［12］.故障树分析法，将物理系统转化为结构化的逻辑图.它主要考虑了基本事件、环境条件和人为条件导致的系统故障.故障树分析法对光伏系统可靠性研究而言是一种有效的工具.当然，需要大量的实验和观测数据来完善故障树的基本事件的建立.故障树的分析一般有4个步骤［13］：（1）系统的定义；（2）故障树结构的搭建；（3）定性分析；（4）定量分析.文献［14－15］基于故障树方法对光伏电站可靠性进行了分析.

本文提出了一种基于故障树分析理论的集中式光伏电站的可靠性评价方法.首先分析了集中式光伏电站的电气结构特点；然后结合故障树理论，给出了集中式光伏发电系统的可靠性数学模型；接着，引用文献中的光伏电站参数，对该模型和指标体系进行了评估和验证，给出了各器件对光伏电站可靠性影响的优先级顺序，其中逆变器对电站的影响最为重要，光伏组件串保护器、光伏组件、交流电路断路器3个器件是次级重要，其他器件的影响相对较小.

1 集中式光伏电站的电气结构模型

典型的集中式并网光伏电站如图1所示，主要器件依次是光伏组件、串接保护装置、直流开关、蓄电系统与控制器、逆变器、交流断路器、电网保护装置、交流开关、差动电路断路器.

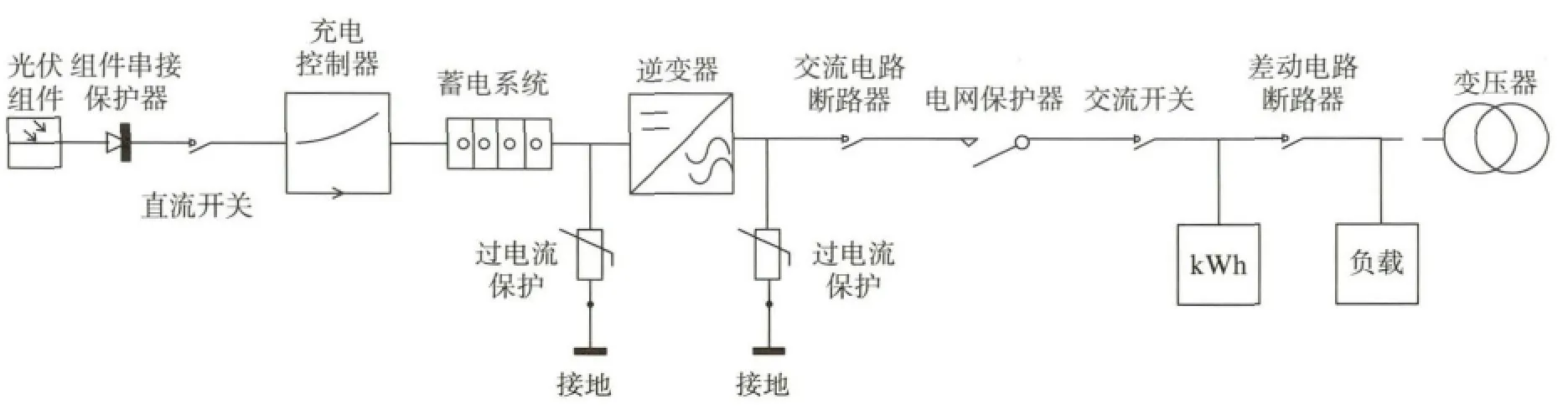
图1 集中式光伏电站电气结构示意图Fig.1 Electrical structure diagram of centralized PV station

光伏组件串和逆变器连接有保护装置，防止逆电流进入光伏组件造成局部阴影效应，一般会采用阻隔二极管、保险丝或断路器.光伏组件串的保护装置之后连接直流开关，可以使维护人员在太阳照射下断开光伏阵列，达到安全维护的目的.直流开关之后，充电控制器调节来自光伏组件的一部分电能到蓄电系统，并保证电能不过充.蓄电系统的电能可在紧急状态下使用，如用于夜晚和多云天气.逆变器模块实现了直流到交流的转换.过载保护装置保护逆变器的输入端和输出端在闪电直接或间接袭击装置引起的激增电流时免受影响.逆变器的右侧是交流侧，一系列的电路断路器保护交流线路主要由交流断路器、电网保护装置、交流开关和差动电路断路器组成.

本文分析了5个发电功率分别是100，200，500，1 000，2 000kW 的集中式光伏电站［16］，它们的电气结构都满足图1.文中使用的逆变器（100kW）参数（Vmpp，min＝450 V，Vmpp，max＝820 V，Vmax＝1 000 V，IDC，max＝235A）和光伏组件（230W）的参数（ISC＝8.24A，Vmpp＝30.2V，μI＝3.3mA／℃，VOC＝37.2V，Impp＝7.60A，μV＝－120mV／℃）见文献［14］，表1列出了每个电站中使用的各个器件的数量［15］.每个逆变器安装3个直流开关，连接光伏组件串到逆变器.研究分析了这5个光伏系统在20年内的可靠性，平均每天运行8.5h，记失败率单位：失败次数／h.

表1 各个光伏电站中的器件数量Tab.1 Number of components in each PV system

2 评估模型

2.1 故障树模型

采用故障树理论对一个复杂系统进行行为分析，是非常有效的：从分析单一组件之间的关系开始，逐次构建成整体系统之间的关联.集中式光伏系统中的主要设备是通过串联方式连接的（光伏组件采用混合串并联），可以用故障树理论进行分析，将光伏电站的电气结构图，转换为图2的故障树分析图.

如图2所示，圆形图标：表示底事件，是引发电站故障的基本项，发生不需要前端输入；或门（帽子形图标）：表示当或门下面至少有一个事件发生时，或门上方的事件才会发生；长方形图标：故障树的主要模块表示中间事件，可以由其他的中间事件和底事件组合形成.PV 表示光伏组件，BD 表示保护二极管（光伏组件串保护器），CON 表示连接器，DCS表示直流开关，CC 表示蓄电系统控制器，BS 表示蓄电系统，SPD 表示过电流保护装置，INV表示逆变器，CBac表示交流电路断路器，GP表示电网保护器，ACS表示交流开关，DCB 表示差动电路断路器.

图2 集中式光伏电站故障树Fig.2 Fault tree model for centralized PV station

2.2 概率统计与计算

对于故障概率按照指数分布的器件［17］，它的平均故障时间和可靠性概率如下所示：

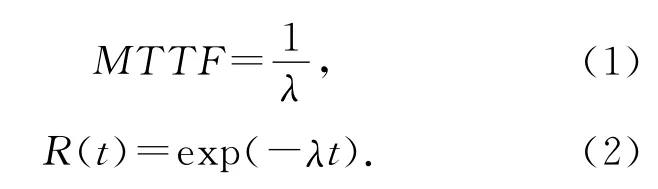
将失效率λ作为器件的可靠性指标，将系统看作是大量的器件通过串联、并联、串并联混合的形式连接在一起.需要说明的是，指数分布函数不是所有电气或电子组件发生故障的最合适的概率函数.实际上，每个光伏器件实际的概率分布密度函数，都需要进行长时间且相对昂贵的加速寿命测试才能得到，得到的数据可能会满足其他分布特征参数函数（如威布尔分布函数）.因此，本文使用指数分布函数，旨在建立一个比较完整的评价体系和方法论.在得到各个组件的真实失效概率分布函数后，只需要代入到该数学模型中，即可得到更加精确的评估结果.

根据文献［5，16，18，19］，可以得到各个器件的失效概率，统计表格如表2所示.逆变器的失效概率计算：外部因素上，与它的光照能量密度、环境温度和输入功率等级密切相关［20］；内部因素上，与其所采用的IGBT、蓄电电容、驱动模块等有着显著关联［21］.在逆变器可靠性研究的文献中，关于其失效概率参数和模型有着较多的讨论，本文不过多展开.根据文献［5］中的逆变器使用情况进行估算：平均9年的运行时间中逆变器发生了1次故障，那么失效率为λ＝1÷（9×365×8.5）＝35.81×10－6.

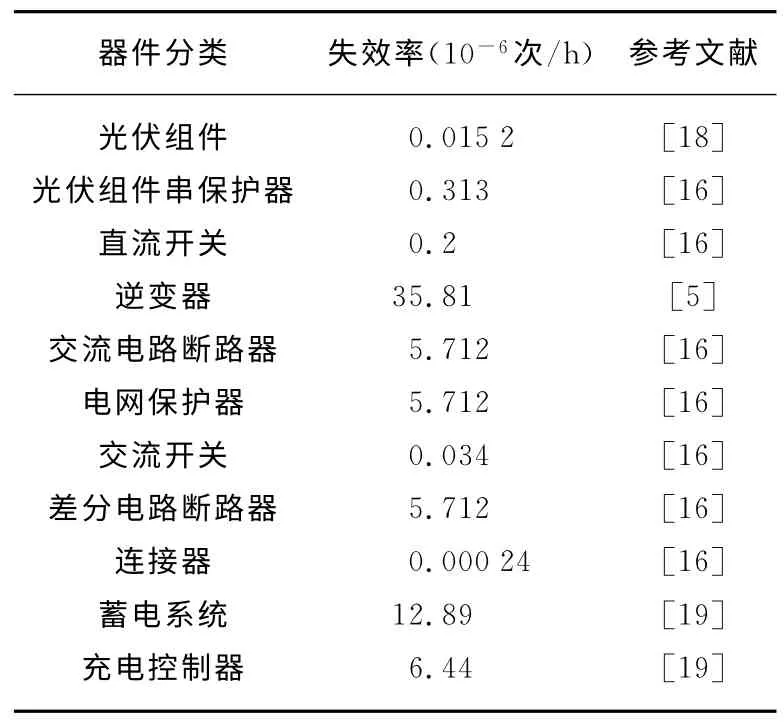
表2 元件采取的失效率Tab.2 Failure rates of components

在定量评估时，将图2 的故障树整合为布尔代数方程如下（其中的SPD 故障率很低，近似为0，即SPD＝0，可忽略）：

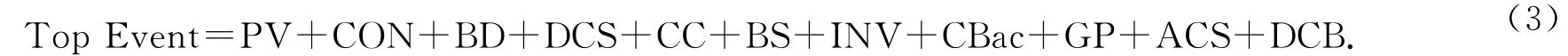
由上式可知：本文中的故障树分析主要基于这11个最小割集（Minimal Cut Sets，记作MCS）.事件的可靠性概率可以表示为如下方程：

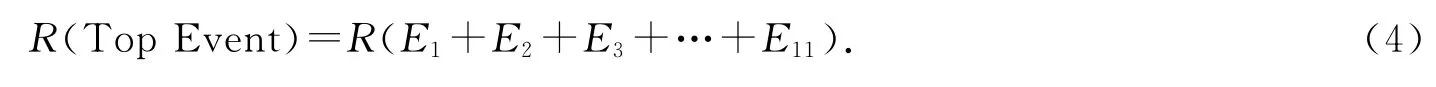
因为各个事件是相互独立事件，令Rtot表示可靠性概率，系统可靠性可以表示为：

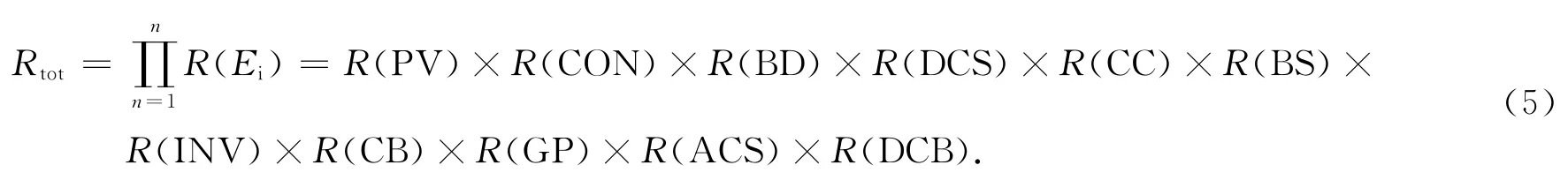
每个组件代入指数分布函数，得到下面的式子：

其中，mi表示总的相同元件的数量，λi表示元件i 的失效率，n 表示不同元件的种类，ti表示可靠性研究的时间.举例：考察200kW 的光伏电站使用1年的逆变器可靠性指数（其中mi＝2，λi＝0.358 1×10－6，ti＝365×8.5＝3 102.5h）：RPV，tot＝exp（－1×2×0.358 1×10－6×3 102.5）＝0.800 7.

3 数据验证和讨论

3.1 数据验证

将表2的失效率，代入到集中式光伏电站各个器件的方程，可得到5个光伏电站的器件在20年后的可靠性评价表（表3）和可靠性趋势图（图3），以及2MW 电站在20年内的可靠性评价表（表4）和可靠性趋势图（图4）.而光伏电站的可靠性评价如表5所示，其中的可靠性概率为0.00%，表示光伏电站中有器件发生故障无法工作，导致光伏电站无法满功率输出，但不必然导致停止功率输出.

表3 光伏电站运行20年后各器件可靠性Tab.3 Total component reliability of each centralized PV station after 20years of operations

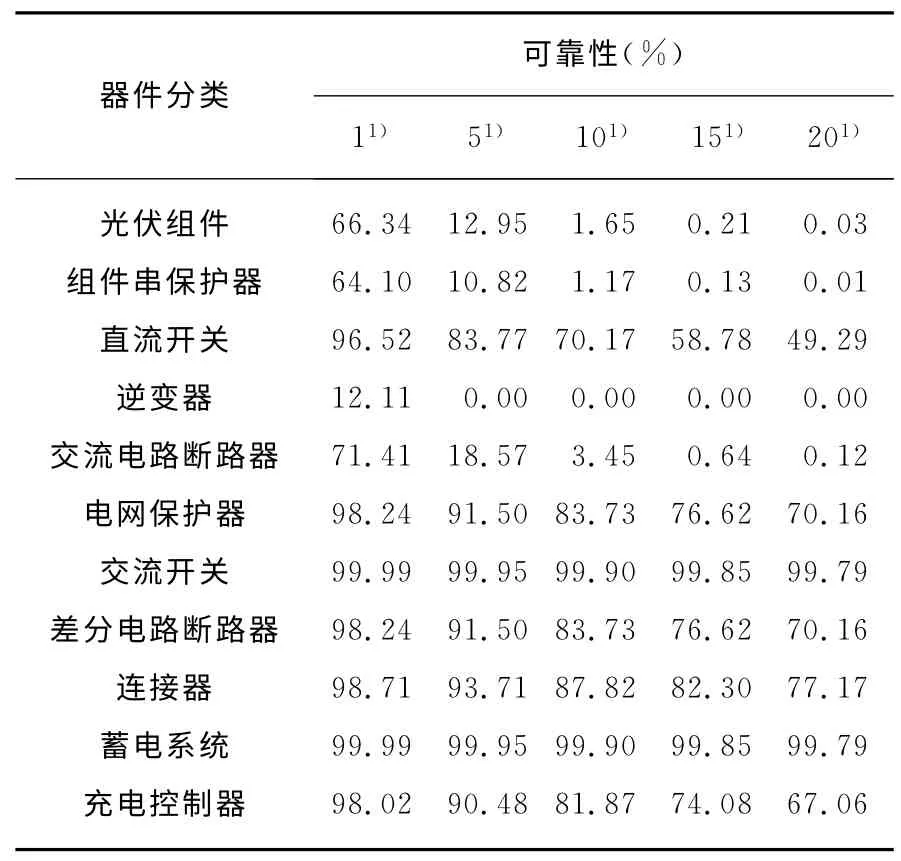
表4 2MW 光伏电站20年各器件可靠性Tab.4 Total component reliability of 2 MW centralized PV station during 20years of operations

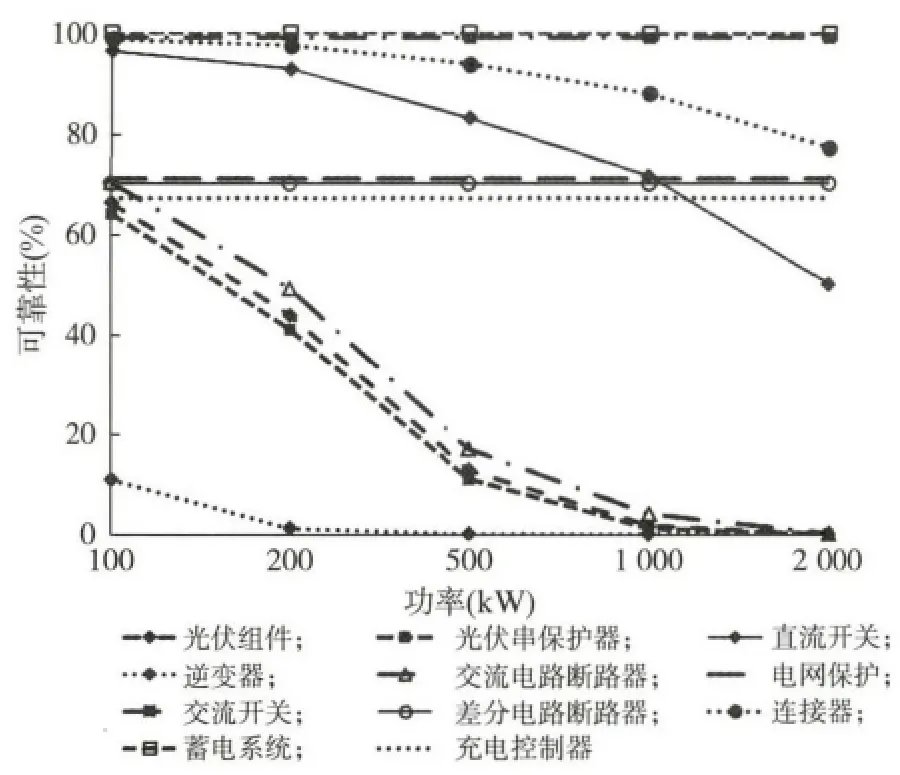
图3 集中式光伏电站运行20年后各器件可靠性Fig.3 Total component reliability of each centralized PV station after 20years of operations

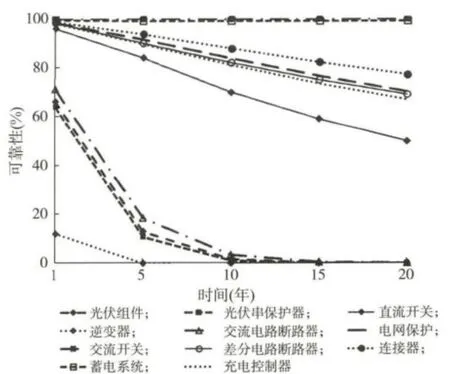
图4 2MW 集中式光伏电站运行20年内各器件可靠性Fig.4 Total component reliability of 2 MW centralized PV station during 20years of operations

为了考察光伏发电系统中，每一个组成部分对系统可靠性的影响程度，用福赛尔法（Fussel－Vesely）来表示.公式如下所示：

比如，计算100kW 光伏电站的直流开关运行20年的FV 值（其中mi＝3，λi＝0.2×10－6，ti＝20×365×8.5＝62 050h）：FV＝1－exp（－1×3×0.2×10－6×62 050）＝0.036 5.

用FV 法计算出光伏系统运行20年，各个器件对光伏系统的影响值，如表6和图5所示.

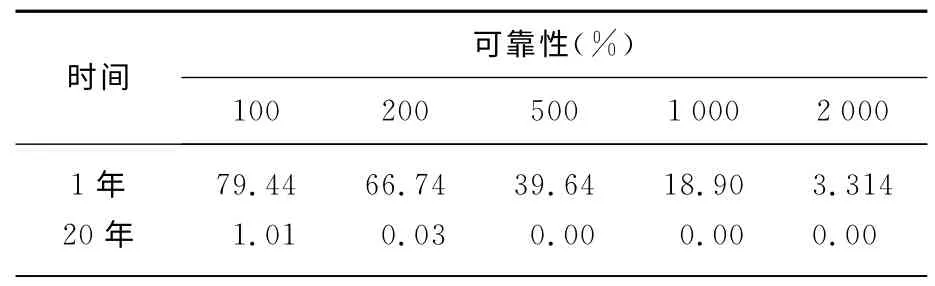
表5 光伏电站整体系统的可靠性Tab.5 System reliability of each centralized PV station for 1and 20years of operation

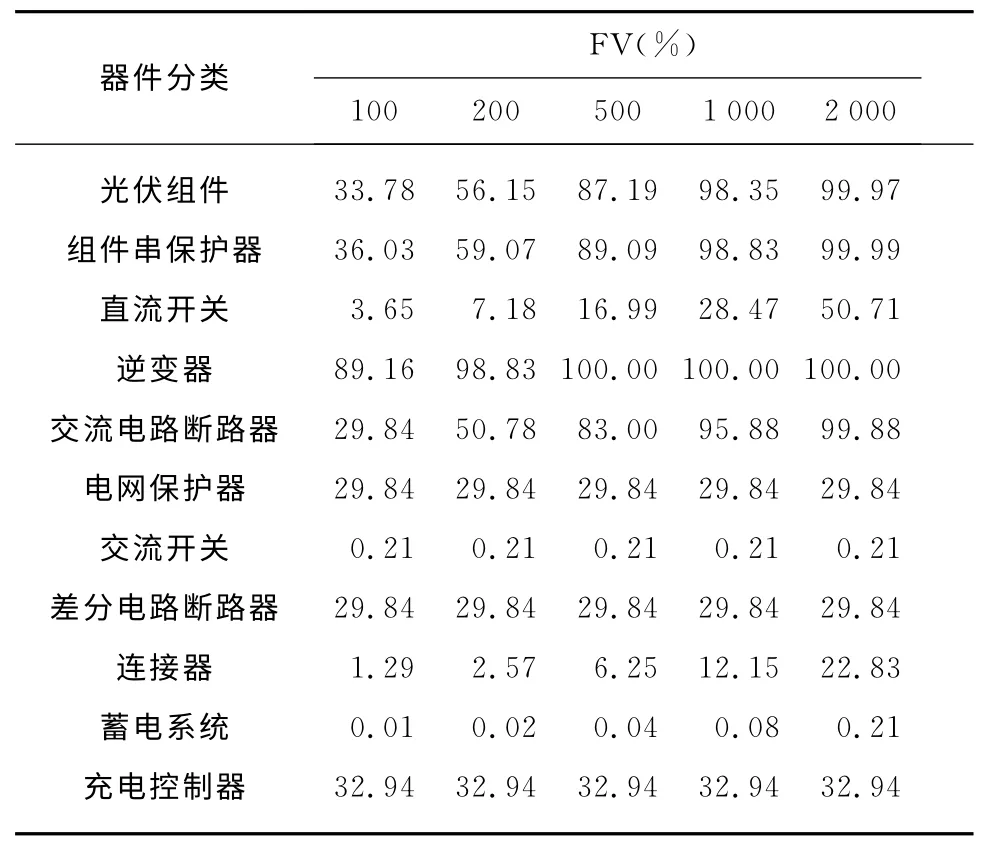
表6 光伏电站运行20年各器件FV结果Tab.6 FV value of components to PV station after 20years of operations

图5 20年后集中式光伏电站各器件对系统的影响值Fig.5 FV value of components to PV station after 20years of operation

3.2 讨论

（1）输出功率

从图3可以看出：随着光伏电站输出功率的增加，光伏电站的可靠性逐渐降低.比如，20年后100kW电站的直流开关正常工作的可靠性概率是96.35%，光伏组件的可靠性概率是66.22%；而20年后2MW电站的直流开关可靠性是49.29%，光伏组件的可靠性只有0.03%.另一方面，逆变器的可靠性衰减最为明显，其次是光伏组件串保护器、光伏组件、交流电路断路器这3类器件，其他器件随着功率的增加，可靠性概率仍然在较高的水平.

（2）运行时间

从图4可以看出：随着运行时间的增长，光伏电站各个器件的可靠性指标会迅速下降.比如，1年后2MW电站的光伏组件的可靠性有66.34%，而20年后正常工作的可靠性概率是0.03%.这意味着如果不进行定期维修，那么大功率的光伏电站经过长时间运行后，将无法正常工作.

（3）器件类别

从图5可以看出：逆变器对光伏系统的影响最为重要，其次是光伏组件串保护器、光伏组件、交流电路断路器这3 种器件，其他的器件对光伏电站的影响程度明显低于前面提到的器件.因此，可以根据这些器件对光伏电站可靠性的影响程度，分成3个大类，如表7所示.在实际的电站维护中，可以根据所分的等级制定不同程度和频率的故障检测和维修策略.这样既保证了重要器件的检测效率和运行可靠性，又降低了电站运维的规模和开销.

针对光伏能源迅速发展的现状，光伏电站的可靠性评估和寿命预测是急需解决的技术难题.本文提出了一种基于故障树理论的集中式光伏电站的可靠性评价方法.文章通过分析集中式光伏电站的电气结构模型，列出了影响电站可靠性的主要事件，然后以最小割集的形式将各个事件组合起来，提出了整个系统的可靠性函数模型.

本文提出了光伏电站中各个器件对系统可靠性影响的优先级分类.其中逆变器对电站的影响最重要，光伏组件串保护器、光伏组件、交流电路断路器3个器件是次级重要，其他器件的影响相对较小.以后的研究工作中，可以根据实际光伏电站的类型，对重点器件进行深入的可靠性研究.根据文章的评价方法，制定灵活高效的光伏检测系统，进而提升光伏电站整体系统的可靠性.

表7 影响光伏电站可靠性的器件优先级Tab.7 Ranking of components for PV station reliability

［1］国家能源局.国家能源局综合司关于征求2015年光伏发电建设实施方案意见的函［R］.北京：国家能源局，2015.

［2］王 敏，宗炫君，袁 越，等.含光伏电站的发电系统可靠性分析［J］.中国电机工程学报，2013，33（34）：42－49.

［3］王 震，鲁宗相，段晓波，等.分布式光伏发电系统的可靠性模型及指标体系［J］.电力系统自动化，2011，35（15）：18－24.

［4］汪海瑛，白晓民，马 纲.并网光伏电站的发电可靠性评估［J］.电网技术，2012，36（10）：1－5.

［5］Ristow A，Begovic M，Pregelj A，et al.Development of a methodology for improving photovoltaic inverter reliability［J］.IEEE Transactions on Industrial Electronics，2008，55（7）：2581－2592.

［6］Maish A B，Atcitty C，Hester S，et al.Photovoltaic system reliability［C］∥1997IEEE 26th Photovoltaic Specialists Conference（PVSC）.Anaheim，CA，USA：IEEE Press，1997：1049－1054.

［7］Kishore L N，Fernandez E.Reliability well－being assessment of PV－wind hybrid system using Monte Carlo simulation ［C］∥2011 IEEE International Conference on Emerging Trends in Electrical and Computer Technology（ICETECT）.Nagercoil，India：IEEE Press，2011：63－68.

［8］Subcommittee P M.IEEE reliability test system［J］.IEEE Transactions on Power Apparatus and Systems，1979，98（6）：2047－2054.

［9］Dhople S V，Davoudi A，Chapman P L，et al.Integrating photovoltaic inverter reliability into energy yield estimation with Markov models［C］∥2010IEEE 12th Workshop on Control and Modeling for Power Electronics（COMPEL）.Colorado，USA：IEEE Press，2010：1－5.

［10］Dhople S V，Domínguez－García A D.Estimation of photovoltaic system reliability and performance metrics［J］.IEEE Transactions on Power Systems，2012，27（1）：554－563.

［11］Collins E，Dvorack M，Mahn J，et al.Reliability and availability analysis of a fielded photovoltaic system［C］∥2009IEEE 34th Photovoltaic Specialists Conference（PVSC），Philadelphia，Pennsylvania，USA：IEEE Press，2009：2261－2266.

［12］Catelani M，Ciani L，Cristaldi L，et al.FMECA technique on photovoltaic module［C］∥2011IEEE Instrumentation and Measurement Technology Conference（I2MTC）.Hangzhou，China：IEEE Press，2011：1717－1722.

［13］Lee W S，Grosh D L，Tillman F A，et al.Fault Tree Analysis，Methods，and Applications－A Review［J］.IEEE Transactions on Reliability，1985，34（3）：194－203.

［14］Zini G，Mangeant C，Merten J.Reliability of large－scale grid－connected photovoltaic systems［J］.Renewable Energy，2011，36（9）：2334－2340.

［15］Ahadi A，Ghadimi N，Mirabbasi D.Reliability assessment for components of large scale photovoltaic systems［J］.Journal of Power Sources，2014，264：211－219.

［16］Lockheed M.Reliability prediction of electronic equipment［M］.Washington D C，USA：HIS Press，1991.

［17］Yang G.Life cycle reliability engineering［M］.Michigan，USA：John Wiley ＆Sons，2007.

［18］Oozeki T，Yamada T，Kato K，et al.An analysis of reliability for photovoltaic systems on the field test project for photovoltaic in Japan［C］∥Solar World Congress of the International－Solar－Energy－Society.Beijing，China：Springer Press，2007：1628－1632.

［19］Kabambalika L.Simulation and performance evaluation of battery based stand－alone photovoltaic systems of Malawi［D］.Taoyuan，China Taiwan：National Central University，2009.

［20］Wang Y，Zhang P，Li W，et al.Comparative analysis of the reliability of grid－connected photovoltaic power systems［C］∥Power and Energy Society General Meeting.San Diego，CA，USA：IEEE Press，2012：1－8.

［21］周雒维，吴军科，杜 雄，等.功率变流器的可靠性研究现状及展望［J］.电源学报，2013，11（1）：1－15.