基于LLL算法的永久散射体差分干涉相位解缠

刘朝功

(天津土地交易中心，天津 300042)

在含有载波相位的数据处理中，正确求取整周模糊度的估值是很重要的环节。永久散射体技术在2001年由Ferretti 提出［1］，其相位解缠也属整数最小二乘范畴。荷兰Delft 大学的Teunissen教授对模糊度提出LAMBDA 解法［2］，并通过Z 变换对模糊度协方差降相关处理。由于Z 变换对整周模糊度的搜索影响很大，近期不同的整周模糊度约化方法大量提出，包括LLL 方法［3，4］、联合去相关［5］等。LLL 方法受到了越来越多的关注，本文基于此进行永久散射体差分干涉相位解缠。

1 永久散射体差分干涉相位解缠

假设永久散射体差分干涉图已经生成且永久散射体点筛选出，对同一幅干涉图K 中的相邻永久散射体点X 和点Y 做相位差分，可以得到函数模型［6-9］。

其中，Δhx为目标点相对于参考面的高程为相位高程转换系数;αd·pd为地表位移的模型;e 中包含大气误差，轨道误差，以及噪声等等随机误差。

因差分相位值是经过取模处理的，真相位差值应加上相应的整周数，故对于K 幅干涉图中的X 点和Y 点，做相位差分，有如下的函数模型(3)。假设已知地表形变的先验模型，且位移函数模型为线性位移α，那么上式中未知参数的个数是K+2，方程的个数是K，观测方程秩亏，不能得出唯一解，为此增加伪观测方程(4)。

协方差矩阵为:

其中，矩阵y1，A1和B1的含义如式(3)定义;A2为一个零矩阵02×K，B2为一个单位矩阵I2×2，观测值y2的值设为0。那么永久散射体差分干涉的函数模型和随机模型可以写为:

2 利用LLL 方法构造Z 变换

对于整数最小二乘，第一步是求出未知参数的浮点解，对模糊度方差协方差矩阵进行乔列斯基分解，用LLL 方法对权矩阵的基进行整数施密特正交变换，构造Z 变换矩阵，那么变换后的方差协方差矩阵就能够近似为一个对角矩阵，再搜索整数解，可以大大简化整周模糊度的搜索时间。基本流程图如图1 所示。

图1 基于LLL 方法的永久散射体差分干涉解缠

假设有如下的函数模型，先进行实数最小二乘求解。

其中，y∈Rn;e∈Rn;x1∈Rm1;x2∈Rm2;A1∈Rn×m1;A2∈Rn×m2，参数x1是整周模糊度，1=［1，…，m1］'是由x1得到的最小二乘解的列向量。根据加权最小二乘原理:

对b=［b1，…，bm1］'进行整数施密特变换，其中，μij=［＜bi，。

为了提高基的正交性，整数施密特变换需要进行迭代计算，最后得到D+E 矩阵是近似对角矩阵，可以快速进行整周模糊度搜索。

3 仿真模拟实验

为了验证LLL 算法的正确性及可行性，利用随机模拟数据进行检验。信号模拟按照ERS1 和ERS2 的卫星参数来设置。一般情况下，主影像的噪声水平比较小，模拟的主影像的相位噪声设置为均值150;副影像的噪声设置为均值200，均方差设置为50;垂直基线方差为400 m，时间基线跨度为8年;大气信号方差2 rad;位移信息10 mm/年的速度方差;DEM 方差为40 m，模拟过程中高程小于0 的设置为0，当作海平面。一般情况下设先验的主SLC 影像的相位方差因子为(200)2，副影像的相位方差因子为(300)2。按照上述参数值，模拟真实的相位再取模，作为观测值用LLL 方法进行解算其整周值。数据模拟的信息如表1所示。

表1 永久散射体数据模拟信息

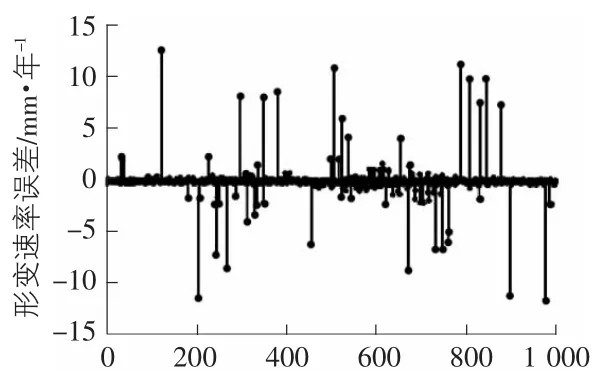
图2 模拟数据和解算结果的形变速率误差

图3 模拟数据和解算结果的DEM 误差

将模拟数据和解算结果做差，统计结果如图2，图3 所示，除个别点DEM 误差最大167 m，形变误差最大12 mm/年，95%以上的数据分布在0 左右，LLL 方法的解算结果是正确和可靠的。

4 结语

永久散射体差分干涉相位解缠是整数最小二乘的一种，本文尝试用LLL 算法构造变换矩阵，对模糊度矩阵约化，并用模拟数据进行算法的验证。该方法可以解算出正确和可靠结果，出现个别点误差很大的原因主要是LLL 方法计算正交基迭代收敛因子追求绝对正交，导致有些点发散不能收敛，这对下一步研究优化LLL 算法具有一定的启发性。

［1］Ferretti A.，Prati C.，Rocca F..Permanent scatterers in SAR interferometry［J］.IEEE Transactions on Geoscience and Remote Sensing，2001，39(1) :8-19.

［2］Teunissen，P.J.G.Least-squares estimation of the intger GPS ambiguities.Invited lecture，section IV Theory and Methodology.IAG General Meeting.Beijing，1993.

［3］Hassibi A，Boyed S.Integer parameter estimation in linear models with applications to GPS.IEEE Transactions on Signal Processing，1998，46(11) :2938-2952.

［4］Grafarend E.W.Mixed integer-real valued adjustment(IRA)problems:GPS initial cycle ambiguity resolution by means of the LLL algorithm［J］.GPS Solutions，2000(4) :31-44.

［5］L.T.Liu，H.T.Hsu，Y.Z.Zhu，etc..A New approach to GPS ambiguity decorrelation［J］.Journal of Geodesy，1999(73) :478-490.

［6］Kampes B.，Hanssen R.F.，Perski Z..Radar Interferometry with public Domain Tools.Proceedings of Fringe 2003 Workshop.Frascati，Italy，2003.

［7］Kampes B M，Hanssen Ramon F.Ambiguity resolution for permanent scatterer interferometry［J］.IEEE Transactions on Geoscience and Remote Sensing，2004，42(11) :2446-2453.

［8］Kampes B.M.，Usai S..Doris:the Delft Object oriented Radar Interferometric Software，2nd International Symposium on Operationalization of Remote Sensing，Enschede，The Netherlands，1999.

［9］Kampes B.M.Radar Interferometry:Persistent Scatterer Technique.Kluwer Academic Publishers，Dordercht，The Netherlands，2006.

［10］Hooper A.，Zebker H.A.，Segall P.，et al.A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers.Geophysical research letters，2004，31(11) :1-5.

［11］Hooper A.Persistent Scatterer Radar Interferometry for Crustal Deformation Studies and Modeling of Volcanic Deformation［D］.Stanford University，2006.