单向玻璃纤维增强树脂基体复合材料拉伸失效机理

郑吉良， 孙 勇， 彭明军

(昆明理工大学 材料科学与工程学院，昆明650093)

纤维增强树脂基体复合材料具有强度高、抗蠕变与高回弹性等优点，已被广泛应用于航空、航天、石油与建筑等各个行业［1～3］。研究表明，该类复合材料力学性能很大程度上依赖于纤维在基体中的埋深长度、基体对纤维包裹厚度以及纤维与基体间界面黏结强度。何先成等［4］自制CCF300级碳纤维U-3160 织物增强环氧树脂复合材料，分析碳纤维含量对复合材料形状记忆性能的影响。钱鑫等［5］研究了碳纤维表面化学结构对其增强环氧树脂基复合材料性能的影响。黄丽等［6］对连续碳纤维增强ABS 热塑性树脂复合材料力学性能、热性能、动态黏弹性及微观形貌进行研究，并分析该复合材料制备工艺对界面性能的影响。Yuan等［7］制备了有机无溶剂聚丙烯酸纳米乳液作为碳纤维上浆剂，通过碳纤维/PES 树脂复合材料揭示范德华力在界面处起到的作用。卢杰等［8］研究了纤维含量和纤维长度对酚醛泡沫压缩性能影响规律，对比了不同的增强形式纤维增强酚醛泡沫复合材料的压缩性能与保温性能。Pyo 等［9］研究了单向纤维增强金属基复合材料在横向载荷下，界面从完好无损到渐渐受损情况下弹塑性损伤模型。Liu 等［10］利用乙烯基酯乳液型上浆剂使得碳纤维/乙烯基酯的材料层间剪切强度提高了21%。纤维长径比影响因素一直是纤维增强复合材料力学领域研究的重点，国内外学者都建立了纤维长径比理论模型［11～16］。Schaller［17］研究了碳纤维增强Mg-2%Si(质量分数)基复合材料界面性质，发现长碳纤维与镁界面结合得相当牢靠，该材料弹性模量是普通钢材或铝合金的4 倍。Singletary等［18］与Schuller 等［19］应用断裂理论对纤维拔出实验与微滴脱粘实验破坏过程进行模拟分析，并能很好符合与解释实验数据。

上述纤维增强基体复合材料力学性能理论计算模型，大部分都假设界面应力沿着纤维轴向均匀分布而得出一个应力值，此值只能是实际界面应力值的一个均值。而特定工况下，纤维界面的应力并不是均匀分布，并不能反映纤维界面应力真实分布。因此本文作者采用界面应力沿着纤维轴向非均匀分布理论模型计算复合材料力学性能。由于单向玻璃纤维与树脂基体为脆性材料，取单向玻璃纤维与树脂基体的弹性参数，着重考察单向玻璃纤维在树脂基体中的埋深长度与树脂对单向玻璃纤维包裹厚度对该类复合材料界面应力分布方式的影响;同时研究单向玻璃纤维与树脂基体界面黏结强度分布形式对该类复合材料破坏方式的影响。

1 实验材料及实验过程

按照GB/T 1447—2013《纤维增强塑料拉伸性能试验方法》规定设计实验样品与实验。单向玻璃纤维布为双层，纤维布长为1160mm，宽为900mm。ARALDITELY 1564 SP 树脂的用量为775g，RSTONE 3486 BLUE CI 胺类固化剂用量为230g，曼尼希碱用量为60g。应用真空灌注方法对单向玻璃纤维布进行注胶，并在真空保压状态下80℃恒温固化8h，制备玻璃纤维含量约70%的面板实验样品。采用日本岛津SHIMADZU Model AG-JS万能材料试验机给定2mm/min 加载速率进行拉伸实验，试件拉伸过程及破坏形式见图1。试件失效瞬间，会听见断裂声音，同时试件出现发白现象，即单向玻璃纤维与树脂基体脱粘。试件在夹持端部附近发生破坏，试件中段位置尚未达到材料强度极限。获得试件应力-应变曲线，并与模拟计算获得应力-应变曲线进行比较。

图1 试件拉伸过程及破坏形式 (a)试件拉伸过程;(b)试件破坏方式Fig.1 Tensile process and damage forms for test sample(a)tensile process for test sample;(b)damage forms for test sample

2 单向玻璃纤维增强树脂基体复合材料拉伸破坏有限元分析

2.1 有限元模型

本工作在商用有限元软件ANSYS 静力分析模块中，建立圆柱纤维嵌入同心圆柱基体中的轴对称Whitney 和Riley 平面模型。有限元模型与网格见图2。图2a 中左侧白体为单向玻璃纤维，右侧黑体为树脂基体。网格采用四边形壳单元，应用网格自动划分方法，生成纯四边形网格，见图2b。

图2 Whitney 和Riley 轴对称平面模型及网格(a)平面模型;(b)网格Fig.2 The axis symmetric plane model and mesh element for Whitney and Riley (a)plane model;(b)mesh element

考察试件模拟计算与实验获得的应力-应变对比曲线时，根据试件中单向玻璃纤维体积分数约70%工况，取单向玻璃纤维半径为rf=2.5μm，树脂基体对单向玻璃纤维包裹厚度为rm=0.5μm，单向玻璃纤维在树脂基体中的埋深长度lf=100μm;单向玻璃纤维弹性模量Ef=64GPa，泊松比νf=0.2，树脂基体弹性模量Em=3GPa，泊松比νm=0.35［20］。单向玻璃纤维含量较高工况下，根据单向玻璃纤维断裂是试件彻底失效主要原因的理论，对图2 中有限元模型进行边界条件设置。树脂基体上下端与单向玻璃纤维下表面给定法向无摩擦约束，单向玻璃纤维与树脂基体界面结合完好，单向玻璃纤维y 轴为对称轴，单向玻璃纤维上表面给定拉应力载荷，观察单向玻璃纤维最大等效应力的变化，以单向玻璃纤维最大等效应力达到单向玻璃纤维本体破坏应力为收敛最后一步，取单向玻璃纤维上表面拉应力值折算的拉力F1与树脂基体上表面法向无摩擦约束的支反力F2，使F1与F2相加，并除以图2 中模型上表面整体面积，得到应力-应变曲线应力值，取收敛最后一步时图2 中模型等效应变最大值，作为应力-应变曲线中应变值。

考察单向玻璃纤维在树脂基体中的埋深长度变化对单向玻璃纤维界面力学性能分布影响时，rf=2.5μm，rm=0.2rf;考察树脂基体对单向玻璃纤维包裹厚度变化对界面力学性能分布影响时，rf=2.5μm，lf=12rf。树脂基体上下端与单向玻璃纤维下表面给定法向无摩擦约束，单向玻璃纤维与树脂基体界面结合完好，y 轴为对称轴，单向玻璃纤维上表面给定拉应力载荷P=1MPa。

2.2 结果分析

模拟计算获得试件应力-应变曲线与实验获得试件应力-应变曲线对比图，见图3。

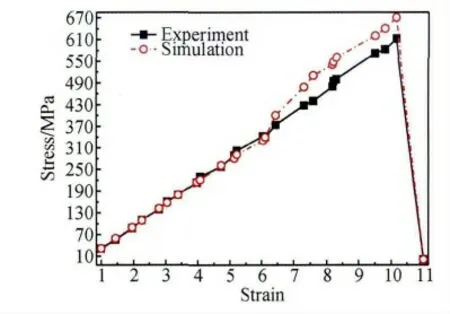
图3 模拟与实验应力-应变对比曲线Fig.3 The stress-strain curve for the experiment results compared with the simulation results

本工作模拟计算获得试件应力-应变曲线与实验获得应力-应变对比曲线开始部分吻合较好，说明有限元模型的准确性。同时模拟计算获得试件断裂瞬间最大应力明显大于实验获得的最大应力，主要原因是现实中单向玻璃纤维与树脂基体界面结合并不是全部完好或者试件存在有缺陷单向玻璃纤维，因此模拟计算获得试件最大应力大于实验获得的最大应力。

考察单向玻璃纤维在树脂基体中的埋深长度对试件界面应力分布影响时，得到导致界面破坏不仅是平行于界面剪应力集中，而且还存在垂直于界面正应力集中。树脂基体对单向玻璃纤维包裹厚度一定，单向玻璃纤维在树脂基体中的埋深长度变化时，从单向玻璃纤维界面剪应力沿单向玻璃纤维y 轴方向分布(见图4)可以看出:剪应力在界面上端出现应力集中，随之快速减小，之后趋于稳定值，但剪应力在界面下端迅速增大，又出现剪应力集中。从单向玻璃纤维界面正应力沿单向玻璃纤维y 轴方向分布(见图5)可以看出:在单向玻璃纤维界面上端存在正应力集中现象，与单向玻璃纤维x 轴正方向同向，使界面产生剥离，离开单向玻璃纤维界面上端附近后，正应力绝对值快速减小并趋于稳定，但在下端又形成正应力集中，与单向玻璃纤维x 轴负方向相同，即为压应力。随着单向玻璃纤维埋深长度加深，单向玻璃纤维界面上下端应力绝对值随之减少(见图4 与5)，但单向玻璃纤维上下端界面正应力类型未发生转变，并且这种减小趋势随单向玻璃纤维埋深长度加深而趋向平稳(见图6 与7)。根据图4 ～7 综合分析可知:树脂基体对单向玻璃纤维包裹厚度一定与试件承载沿着单向玻璃纤维排布方向拉伸载荷工况下，单向玻璃纤维在树脂基体中的埋深长度应保持最佳的范围内，高过一定值后增强作用几乎不再增加，过低又不能保证复合材料足够力学性能。

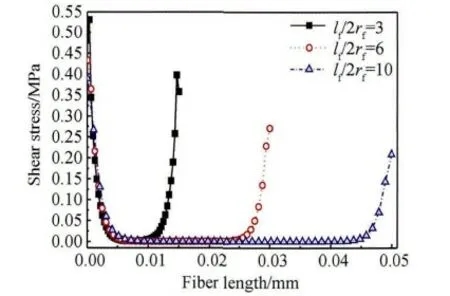
图4 纤维埋深变化时界面剪应力沿纤维y 轴正方向分布Fig.4 The distribution of interfacial shear stress along positive y axis of fiber while fiber embedded length varied

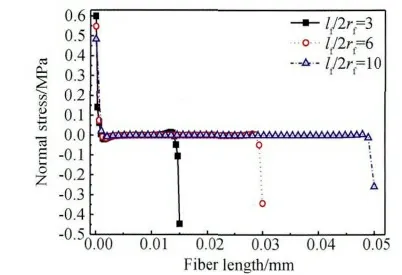
图5 纤维埋深变化时界面正应力沿纤维y 轴正方向分布Fig.5 The distribution of interfacial normal stress along positive y axis of fiber while fiber embedded length varied

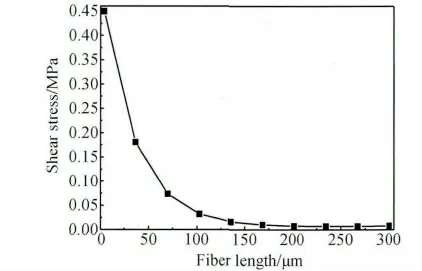
图6 界面剪应力最大值与纤维埋深变化的关系Fig.6 The relationship between maximum interfacial shear stress and fiber embedded length

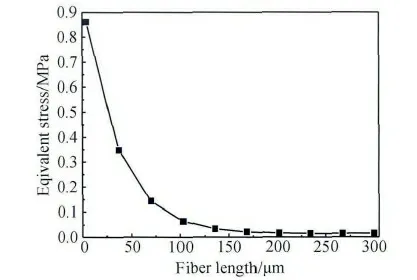
图7 界面等效应力最大值与纤维埋深变化的关系Fig.7 The relationship between maximum interfacial equivalent stress and fiber embedded length

单向玻璃纤维在树脂基体中的埋深长度一定，树脂基体对单向玻璃纤维包裹厚度变化时，从单向玻璃纤维界面剪应力沿单向玻璃纤维y 轴方向分布(见图8)可以看出:剪应力在界面上端出现应力集中，随之快速减小并趋于稳定值，但剪应力在界面下端迅速的增大，又出现剪应力集中。从单向玻璃纤维界面正应力沿单向玻璃纤维y 轴方向分布(见图9)可以看出:单向玻璃纤维界面上端存在正应力集中，与单向玻璃纤维x 轴正方向同向，使界面产生剥离，离开单向玻璃纤维上端点附近后，单向玻璃纤维界面正应力绝对值迅速减小，但单向玻璃纤维界面下端又形成应力集中，却与单向玻璃纤维x 轴负方向相同，即为压应力;随着树脂基体对单向玻璃纤维包裹厚度增大，单向玻璃纤维界面上下端的应力绝对值逐渐地减小(见图8 与9)，并且这种减少趋势也随包裹厚度的增加而趋于平稳(见图10 与11)，同样单向玻璃纤维上下端界面正应力类型未发生转变。根据图8 ～11 综合分析可知:单向玻璃纤维在树脂基体中的埋深长度一定与试件承载沿着单向玻璃纤维排布方向拉力载荷工况下，树脂基体对单向玻璃纤维包裹厚度应保持最佳的范围内，低于一定值后增强作用几乎不再增加，过高又不能保证该复合材料足够力学性能。

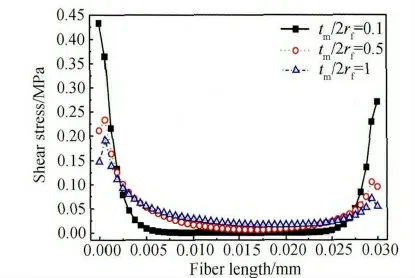
图8 基体包裹厚度变化时界面剪应力沿纤维y 轴正方向分布Fig.8 The distribution of interfacial shear stress along positive y axis of fiber while matrix wrapped thickness varied

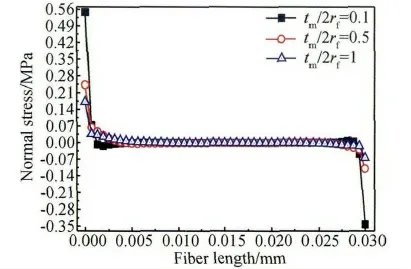
图9 基体包裹厚度变化时界面正应力沿纤维y 轴方向分布Fig.9 The distribution of interfacial normal stress along positive y axis of fiber while matrix wrapped thickness varied

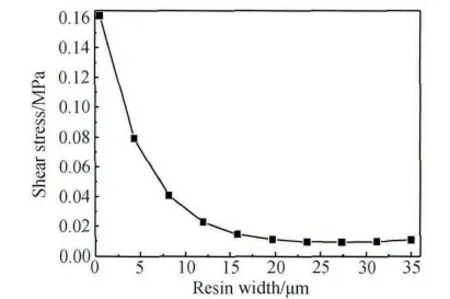
图10 界面剪应力最大值与基体包裹厚度变化关系Fig.10 The relationship between maximum interfacial shear stress and matrix wrapped thickness

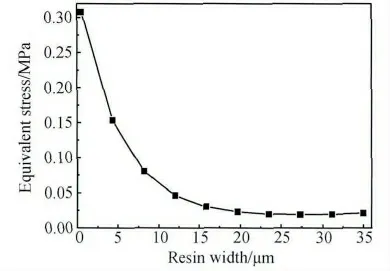
图11 界面等效应力最大值与基体包裹厚度变化关系Fig.11 The relationship between maximum interfacial equivalent stress of fiber and matrix wrapped thickness

综上所述，单向玻璃纤维在树脂基体中的埋深长度与树脂基体对单向玻璃纤维包裹厚度应保持在一个最佳范围，高过一定值后几乎起不到增强作用，过低又不能保证复合材料足够力学性能。同时上述单向玻璃纤维界面应力绝对值在单向玻璃纤维上下端部最大，对试件在夹持端的附近断裂给予很好解释，说明有限元模型准确性。

单向玻璃纤维在树脂基体中的埋深长度与树脂基体对单向玻璃纤维包裹厚度两种因素共同作用工况下，单向玻璃纤维界面剪切应力与等效应力最大值分布三维图，见图12 与13。由图可知:随着单向玻璃纤维在树脂基体中的埋深长度增加，树脂基体对单向玻璃纤维包裹厚度对试件力学性能影响将变得微弱。

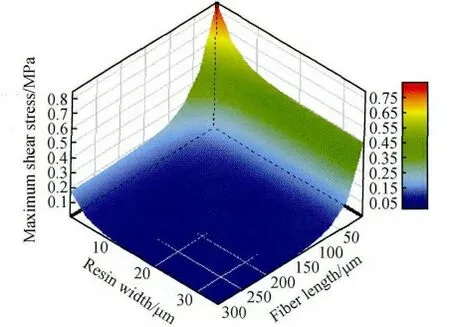
图12 纤维埋深与基体包裹厚度同时变化时纤维界面剪切应力分布图Fig.12 The distribution of interfacial shear stress of fiber while fiber embedded length and matrix wrapped thickness varied together

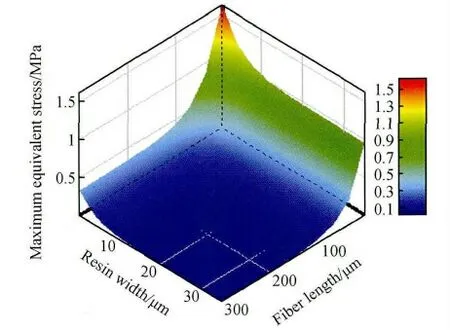
图13 纤维埋深长度与基体包裹厚度同时变化时纤维界面等效应力最大值分布图Fig.13 The distribution of interfacial equivalent stress of fiber while fiber embedded length and matrix wrapped thickness together

3 单向玻璃纤维与树脂基体界面结合强度对试件破坏方式影响分析

3.1 有限元模型

根据试件拉伸实验破坏现象可知:试件断裂位置出现在夹持端的附近，有的试件断裂位置出现在上端夹持部位附近，有的试件断裂位置出现在下端夹持部位附近;同时试件断裂位置出现在上端夹持部位附近时，试件下端夹持部位附近无明显单向玻璃纤维与树脂基体界面脱粘发白现象，然而试件断裂位置出现在下端夹持部位附近时，试件上端夹持部位附近出现明显单向玻璃纤维与树脂基体界面脱粘发白现象。本工作在商用有限元软件ANSYS 静力分析模块中，建立圆柱纤维嵌入同心圆柱基体中轴对称Whitney 和Riley 平面模型，模拟研究拉伸实验中试件不同破坏现象机理，有限元模型与网格见图14。图14a 整体分为两部分:左侧部分为单向玻璃纤维，右侧部分为树脂基体。为了探讨单向玻璃纤维与树脂基体界面结合强度对试件破坏机理影响，把单向玻璃纤维分割成三部分:上、下端部与中间部分，上下端部为图14a 中红色区域，中间部分为图14a 中白色部分。根据前面分析得到单向玻璃纤维上下端界面应力集中范围，给定单向玻璃纤维上下端界面应力集中范围为5μm 长度。网格采用四边形壳单元，应用网格自动划分方法，生成纯四边形网格，见图14b。

图14 Whitney 和Riley 轴对称平面模型及网格(a)平面模型;(b)网格Fig.14 The axis-symmetric plane model and mesh element for Whitney and Riley(a)plane model;(b)mesh element

考察单向玻璃纤维与树脂基体界面结合强度系数对试件拉伸破坏方式影响时，给定rf=2. 5μm，rm=0.2rf，lf=12rf;Ef=64GPa，υf=0.2;Em=3GPa，υm=0.35;树脂上下端与单向玻璃纤维下表面给定法向无摩擦约束，根据公式［K］{x}= {F}，通过改变刚度矩阵常量［K］大小，来改变单向玻璃纤维与树脂界面结合强度，单向玻璃纤维y 轴为对称轴，单向玻璃纤维上表面给定拉应力载荷P =1MPa。

3.2 结果分析

改变单向玻璃纤维与树脂基体中间部分界面结合强度系数，得到单向玻璃纤维界面正应力与剪切应力沿单向玻璃纤维y 轴方向分布曲线，见图15 与16。由图可知:单向玻璃纤维与树脂基体中间部分界面结合刚度矩阵常量［K］对单向玻璃纤维界面应力分布影响很小。说明拉力载荷不能通过界面最大程度传递到单向玻璃纤维中部，充分发挥单向玻璃纤维增强效应，图1 中试件破坏位置在试件上下端夹持部位附近，而试件中间部分完好的破坏现象，由此可以得到进一步解释。

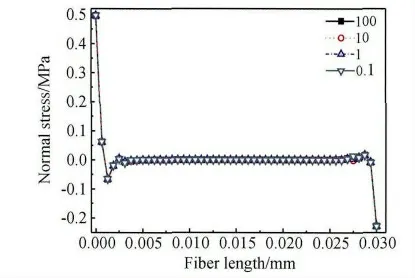
图15 不同纤维与基体中间段结合强度系数下界面正应力沿纤维y 轴方向分布情况Fig.15 The distribution of interfacial normal stress along y axis of fiber under different adhesion coefficient between the fiber and resin in the middle

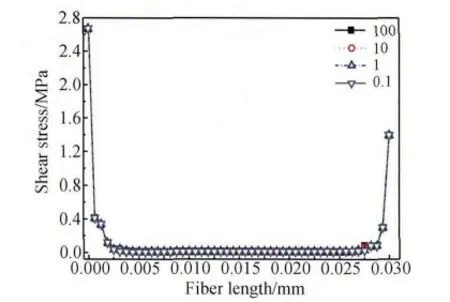
图16 不同纤维与基体中间段结合强度系数下界面剪切应力沿纤维y 轴方向分布情况Fig.16 The distribution of interfacial shear stress along y axis of fiber under different adhesion coefficient between the fiber and resin in the middle

改变单向玻璃纤维与树脂基体上端界面结合强度常量［K］，得到单向玻璃纤维界面正应力与剪应力沿单向玻璃纤维y 轴方向分布曲线，见图17 与18。由图17 可知:随着单向玻璃纤维与树脂基体上端界面结合刚度矩阵常量［K］增大，单向玻璃纤维界面上端正应力绝对值逐渐增大，单向玻璃纤维界面下端正应力绝对值逐渐减小，并且单向玻璃纤维界面上端正应力由分离力逐渐转变为压应力。由于单向玻璃纤维界面应力绝对值在单向玻璃纤维上端最大，拉力载荷将通过界面最大程度传递到单向玻璃纤维上端部，达到单向玻璃纤维能够承受临界应力值，单向玻璃纤维在上端部发生断裂而使试件失效。图1 中的试件在上端夹持部位附近断裂失效时，单向玻璃纤维下端部夹持部位附近没有出现明显发白脱粘现象，主要原因就在于单向玻璃纤维下端界面本身为压应力，因此下端界面很难出现脱粘发白现象。由图18 可知:随着单向玻璃纤维与树脂基体上端界面结合刚度矩阵常量［K］增加，单向玻璃纤维界面上端剪应力值逐渐增大，单向玻璃纤维界面下端剪切应力值大小逐渐减小。改变单向玻璃纤维与树脂基体上端界面结合刚度矩阵常量［K］，得到单向玻璃纤维界面剪切应力与等效应力最大值变化曲线，见图19 与20。由图可知:随着单向玻璃纤维与树脂基体上端界面结合刚度矩阵常量［K］的增加，单向玻璃纤维界面剪切应力与等效应力最大值为先迅速增大，之后变得平缓。单向玻璃纤维界面剪应力与等效应力最大值迅速增大阶段，原因是随着单向玻璃纤维与树脂基体上端界面结合刚度矩阵常量［K］增加，界面上端分离力绝对值逐渐降低，致使通过界面传递到单向玻璃纤维上端载荷增加，因此单向玻璃纤维界面剪应力与等效应力最大值曲线出现迅速增加趋势;单向玻璃纤维界面剪应力与等效应力最大值平缓阶段，原因是随着单向玻璃纤维与树脂基体上端界面结合刚度矩阵［K］增加，界面上端正应力已转化为压应力，外载荷一定工况下，通过界面传递到单向玻璃纤维上端载荷达到极限值，因此单向玻璃纤维界面剪应力与等效应力最大值曲线出现平缓阶段。

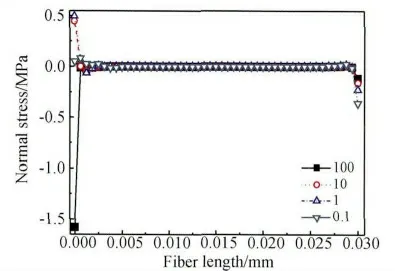
图17 不同纤维与基体上端结合强度系数下界面正应力沿纤维y 轴方向分布情况Fig.17 The distribution of interfacial normal stress along y axis of fiber under different adhesion coefficient between the fiber and resin at the top

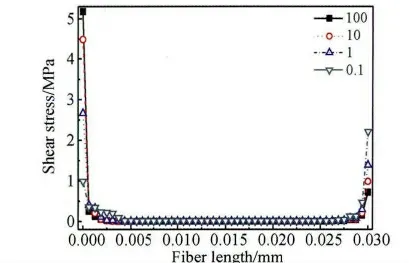
图18 不同纤维与基体上端结合强度系数下界面剪切应力沿纤维y 轴方向分布情况Fig.18 The distribution of interfacial shear stress along y axis of fiber under different adhesion coefficient between the fiber and resin at the top

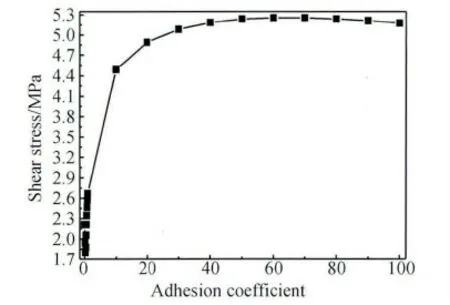
图19 界面剪切应力最大值和纤维与基体上端结合强度系数变化关系Fig.19 The relationship between maximum interfacial shear stress and the varied adhesion coefficient between the fiber and resin at the top

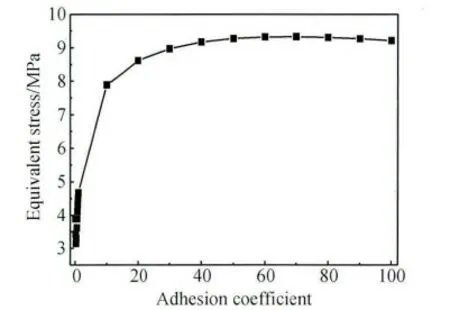
图20 纤维界面等效应力最大值和纤维与基体上端结合强度系数变化关系Fig.20 The relationship between maximum interfacial equivalent stress of fiber and the varied adhesion coefficient between the fiber and resin at the top

改变单向玻璃纤维与树脂基体下端界面结合刚度矩阵常量［K］，得到单向玻璃纤维界面正应力与剪应力沿玻璃纤维y 方向分布曲线，见图21 与22。由图21 可知:随着单向玻璃纤维与树脂基体下端界面结合刚度矩阵常量［K］增大，单向玻璃纤维界面上端正应力绝对值逐渐减小，单向玻璃纤维界面下端正应力绝对值逐渐增大，单向玻璃纤维界面正应力绝对值最后在单向玻璃纤维界面下端最大，同时单向玻璃纤维界面下端正应力由压应力逐渐变为分离力。由单向玻璃纤维界面上下端正应力变化趋势可知:由于单向玻璃纤维界面正应力绝对值最后在单向玻璃纤维界面下端最大，因此试件断裂位置将出现在试件下端夹持部位附近，同时单向玻璃纤维界面上端正应力为分离力，试件断裂瞬间，试件上端加持部位附近出现脱粘发白现象，这是对图1 中左边第一个试件破坏方式的很好解释。由图22 可知:随着单向玻璃纤维与树脂基体下端界面结合刚度矩阵常量［K］增大，单向玻璃纤维界面上端剪应力值逐渐减小，单向玻璃纤维界面下端剪应力值逐渐增大。改变单向玻璃纤维与树脂基体下端界面结合刚度矩阵常量［K］，得到单向玻璃纤维界面剪切应力与等效应力最大值变化曲线，见图23 与24。由图可知:随着单向玻璃纤维与树脂基体下端界面结合刚度矩阵常量［K］增加，单向玻璃纤维界面剪应力与等效应力最大值为先迅速减小，达到最小值后，又逐渐增大，最后变为平缓降低趋势。单向玻璃纤维界面剪应力与等效应力最大值迅速减小阶段，原因是单向玻璃纤维与树脂基体下端界面结合的刚度矩阵常量［K］很低时，单向玻璃纤维界面剪应力与等效应力最大值出现在单向玻璃纤维界面的上端，随着单向玻璃纤维与树脂基体下端界面结合刚度矩阵常量［K］增加，通过界面传递到单向玻璃纤维下端部分载荷增加，因而单向玻璃纤维界面上端剪应力与等效应力最大值迅速降低，单向玻璃纤维界面剪应力与等效应力最大值曲线出现迅速降低现象。单向玻璃纤维界面剪应力与等效应力最大值逐渐增大阶段，原因是随着单向玻璃纤维与树脂基体下端界面结合刚度矩阵常量［K］继续增大时，单向玻璃纤维界面剪应力与等效应力最大值出现在单向玻璃纤维界面下端，同时通过界面传递到单向玻璃纤维下端拉力载荷逐渐增加，因此出现单向玻璃纤维界面剪应力与等效应力最大值出现逐渐上升现象。单向玻璃纤维界面剪应力与等效应力最大值平缓降低阶段，原因是随着单向玻璃纤维与树脂基体下端结合强度常量［K］继续增大，单向玻璃纤维界面下端压应力转变为分离力，使拉力载荷通过界面传递到单向玻璃纤维下端能力降低，因此曲线出现平缓下滑趋势。

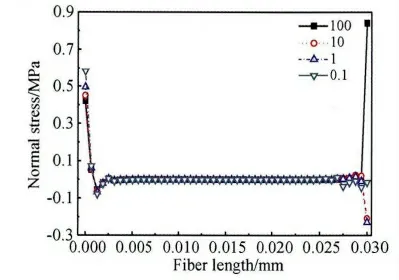
图21 不同纤维与基体下端结合强度系数下界面正应力沿纤维y 轴方向分布情况Fig.21 The distribution of interfacial normal stress along y axis of fiber under different adhesion coefficient between the fiber and resin at the bottom

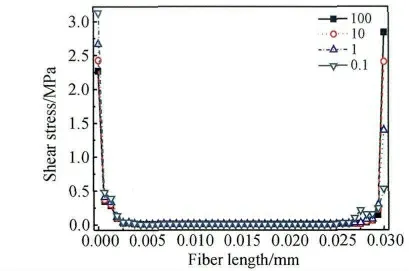
图22 不同纤维与基体下端结合强度系数下界面剪切应力沿纤维y 轴方向分布情况Fig.22 The distribution of interfacial shear stress along y axis of fiber under different adhesion coefficient between the fiber and resin at the bottom

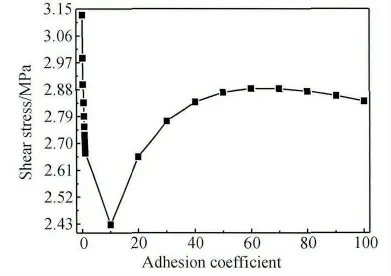
图23 界面剪切应力最大值和纤维与基体下端结合强度系数变化关系Fig.23 The relationship between maximum interfacial shear stress and the varied adhesion coefficient between the fiber and resin at the bottom

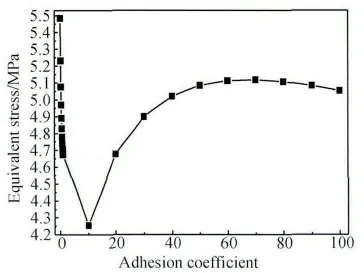
图24 纤维界面等效应力最大值和纤维与基体下端结合强度系数变化关系Fig.24 The relationship between maximum interfacial equivalent stress of fiber and the varied adhesion coefficient varied between the fiber and the resin at the bottom

综上所述，单向玻璃纤维与树脂基体界面上下端结合强度分布方式对试件破坏方式有重要影响。随着纤维与基体上端界面结合强度增加，纤维界面上下端正应力转化为压应力。随着纤维与基体下端界面结合强度增加，纤维界面上下端正应力转化为分离力。

4 结论

(1)单向玻璃纤维增强树脂基体复合材料中纤维含量较高与承载沿着单向玻璃纤维排布方向拉力载荷工况下，随着拉力载荷增大，纤维首先发生断裂，同时由于纤维含量较高，纤维断裂瞬间，树脂基体承载的载荷很大，因而纤维断裂瞬间，树脂基体也随之断裂，致使试件达到最大破坏应力而失效。

(2)导致单向玻璃纤维与树脂基体界面破坏不仅是平行界面剪应力集中，而且还存在垂直界面正应力集中。

(3)单向玻璃纤维在树脂基体中的埋深长度与树脂基体对单向玻璃纤维包裹厚度应保持在最佳的范围内。单向玻璃纤维在树脂基体中的埋深长度高过一定值后增强作用几乎不再增加，过低又不能保证复合材料足够力学性能。树脂基体对单向玻璃纤维包裹厚度低于一定值后增强作用几乎不再增加，过高又不能保证复合材料足够力学性能。

(4)单向玻璃纤维与树脂基体界面结合强度分布形式对试件破坏方式有重要影响。单向玻璃纤维与树脂基体中间部分界面结合强度对单向玻璃纤维界面应力分布方式影响很小。随着单向玻璃纤维与树脂基体上端界面结合强度增加，单向玻璃纤维界面上下端正应力转化为压应力。随着单向玻璃纤维与树脂基体下端界面结合强度增加，单向玻璃纤维界面上下端正应力转化为分离力。

［1］SALEEM M，TOUBAL L，ZITOUNE R，et al. Investigating the effect of machining process on the mechanical behavior of composite plates with circular holes［J］. Composites Part A:Applied Science and Manufacturing，2013，55(2):169 －177.

［2］包建文，陈祥宝. 发动机用耐高温聚酰亚胺树脂基复合材料的研究进展［J］. 航空材料学报，2012，32(6):1－13.(BAO J W，CHEN X B. Advance in high temperature polyimide resin matrix composites for aeroengine［J］. Journal of Aeronautical Materials，2012，32(6):1 －13.)

［3］梁春华，李晓欣. 先进材料在战斗机发动机上的应用与研究趋势［J］. 航空材料学报，2012，32(6):32 －36.(LIANG C H，LI X X. Application and development trend of advanced materials for fighter engine［J］. Journal of Aeronautical Materials，2012，32(6):32 －36.)

［4］何先成，高军鹏，安学锋，等. 环氧树脂基形状记忆复合材料的制备与性能［J］. 航空材料学报，2014，34(6):62－66.(HE X C，GAO J P，AN X F，et al. Fabrication and performance of shape memory epoxy resin composite［J］. Journal of Aeronautical Materials，2014，34 (6):62 －66.)

［5］钱鑫，支建海，张永刚，等. 碳纤维表面化学结构对其增强环氧树脂基复合材料性能的影响［J］. 材料工程，2014(6):84 －88.(QIAN X，ZHI J H，ZHANG Y G，et al. Effect of surface chemical structure of carbon fibers on properties of carbon fiber/epoxy resin composites［J］. Journal of Materials Engineering，2014(6):84 －88.)

［6］黄丽，张祺鑫，王成忠. 连续炭纤维增强ABS 界面性能研究［J］. 材料工程，2013(1):30 －34.(HUANG L，ZHANG Q X，WANG C Z. Interface of continuous carbon fiber reinforced ABS［J］. Journal of Materials Engineering. 2013(1):30 －34.)

［7］YUAN H，ZHANG S，LU C，et al. Improved interfacial adhesion in carbon fiber/polyether sulfone composites through an organic solvent-free polyamic acid sizing［J］.Applied Surface Science，2013，279 (17):279 －284.

［8］卢杰，杨中甲，顾铁卓，等. 玻璃纤维增强体形式对酚醛泡沫性能的影响［J］. 复合材料学报，2014，31(6):1394－1401.(LU J，YANG Z J，GU T Z，et al. Effect of glass fiber reinforcement type on property of phenolic foam［J］. Acta Materiae Compositae Sinica，2014，31(6):1394 －1401.)

［9］PYO S H，LEE H K. An elastic-plastic damage model for metal matrix composite considering progressive imperfect interface under transverse loading［J］. International Journal of Plasticity，2010，26 (1):25 －41.

［10］LIU J，GE H，CHEN J，et al. The preparation of emulsion type sizing agent for carbon fiber and the properties of carbon fiber/vinyl ester resin composites［J］. Journal of Applied Polymer Science，2012，124 (1):864 －872.

［11］HINE P J，LUSTIH R F，GUSEV A A. Numerical simulation of the effect of volume fraction，aspect ratio and fiber length distribution on elastic and thermal-elastic properties of short fiber composites［J］. Compos Sci Tech，2002(62):1445 －1453.

［12］张亚芳，齐雷，张春梅. 增强短纤维长径比对复合材料力学性能的影响［J］. 广州大学学报(自然科学版)，2008，7(4):32 －34.(ZHANG Y F，QI L，ZHANG C M. The effect of aspect ratio on the mechanical behavior of composite［J］. Journal of Guangzhou University (Natural Science Edition)，2008，7 (4):32 －34.)

［13］杜勇峰. 短纤维复合材料中短纤维对基体裂纹的阻滞效应［J］. 合肥工业大学学报(自然科学版)，2002，25(2):277 －280.(DU Y F. Analysis of mechanics of crack bridged by short fiber reinforced composition［J］. Journal of Hefei University of Technology (Natural Science Edition)，2002，25(2):277 －280.)

［14］康国政，高庆. 纤维长径比对单向短纤维复合材料力学行为的影响［J］. 西南交通大学学报，2000，35(2):188－191.(KANG G Z，GAO Q. The effect of fiber aspect ratio on the mechanical behavior of aligned short fiber composites［J］. Journal of Southwest Jiaotong University，2000，35(2):188 －191.)

［15］FAVRE J P. Characterization of fiber/resin bonding in composites using pull-out test［J］. Int J Adhes，2008，1(6):234 －241.

［16］BECKERT W，LAUKE B. Critical discussion of the single fiber pull-out test:does it measure adhesion［J］. Composites Science and Technology，2003，57 (3):1689 －1706.

［17］SCHALLER R. Mechanical spectroscopy of interface stress relax-action in metal-matrix composites［J］. Materials Science and Engineering(A)，2006，442 (1/2):423 －428.

［18］SINGLETARY J，LAUKE B，BECKERT W. Examination of fundamental assumptions of analytical model of fiber pull-out test［J］. Mechanics of Composites Materials and Structures，2007，4 (3):95 －112.

［19］SCHULLER T，BECKERT W，LAUKE B. A finite element model to include interfacial roughness into simulations of micromechanical test［J］. Composites Materials Science，2010，15 (1):357 －366.

［20］郑吉良，孙勇，彭明军. 基于纤维拔出理论的复合材料力学性能的研究［J］. 兵器材料科学与工程，2014，37(2):16 －21.(ZHENG J L，SUN Y，PENG M J. Mechanical properties of composite material based on fiber pull-out theory［J］.Ordnance Material Science and Engineering，2014，37(2):16 －21.)