基于线弹性断裂力学的注塑机拉杆组件的微裂纹稳定要素的研究及应用（上）

张友根，曹亮

（宁波海达塑料机械有限公司，浙江 宁波 315200）

基于线弹性断裂力学的注塑机拉杆组件的微裂纹稳定要素的研究及应用（上）

张友根，曹亮

（宁波海达塑料机械有限公司，浙江 宁波 315200）

基于线弹性断裂力学的微裂纹理论，分析了注塑机拉杆组件的微裂纹稳定要素与断裂之间的关联。纠正了传统的拉杆组件非对称循环的运动力学的特性的观点，首次提出了拉杆组件脉动循环的弹性力学的运动特性的新观点，为科学运用微裂纹稳定的应力强度因子理论奠定了理论基础。创建了微裂纹稳定的应力强度因子的判据理论，解释了拉杆断裂的力学因素，提供了卸载性能的微裂纹稳定的理论设计依据。结合实例，提出了微裂纹稳定的可靠性安全系数均值、承载能力的综合系数、脉动循环屈服强度等三个要素的工业设计理论及应用原则， 提出了微裂纹稳定的卸载段直径、螺纹段底径及拉杆螺母的设计理论及确定原则。研究了线弹性断裂力学要素与弹性力学性能之间、与质量控制之间的关联，探索提高微裂纹稳定的质量要素研发方向。运用创新的拉杆组件的线弹性断裂力学要素的工业设计理论，分析了断裂失效实例，进一步说明线弹性断裂力学要素的微裂纹失稳的研究有助于预测和防止拉杆组件的断裂现象的发生。

注塑机；拉杆组件；线弹性断裂力学；研究；应用

拉杆组件是注塑机的关键部件，也是易断裂失效的组件。断裂的根本因素是拉杆组件的微裂纹失稳及快速扩张，诱发断裂的宏观裂纹，导致疲劳断裂。 研究拉杆组件的线弹性断裂力学的微裂纹稳定的工业设计理论，建立微裂纹失稳判据，对预测和防止注塑机拉杆组件的断裂具有重要意义。本文基于线弹性断裂力学的理论，分析了拉杆组件的微裂纹稳定与断裂失效之间的关联；研究了拉杆组件的弹性力学的运行特征，纠正了传统的拉杆组件非对称循环的力学特性的观点，首次提出了拉杆组件脉动循环的力学特性的新观点，为科学运用微裂纹稳定的应力强度因子理论奠定了理论基础； 创建了微裂纹稳定的应力强度因子的判据理论，解释了拉杆断裂的力学因素，提供了卸载性能的微裂纹稳定的理论设计依据；结合实例，提出了微裂纹稳定的可靠性安全系数均值、承载能力的综合系数、脉动循环屈服强度等三个要素的工业设计理论及应用原则，提出了微裂纹稳定的卸载段直径、螺纹段底径及拉杆螺母的设计理论及确定原则；研究了线弹性断裂力学的微裂纹要素与弹性力学性能之间、与质量控制之间的关联，提出提高微裂纹稳定的质量要素的研发方向；运用创新的拉杆组件的线弹性断裂力学的微裂纹要素的工业设计理论，分析了断裂失效实例，进一步说明线弹性断裂力学要素的微裂纹失稳的研究有助于预测和防止拉杆组件的断裂现象的发生。

图1 油缸驱动的双曲肘斜排列内翻式五支点肘杆机构的合模部件

图2 注塑机的拉杆组件结构简图

1 拉杆组件的功能及动力学特点的简介

图1为目前广泛采用的油缸驱动的双曲肘斜排列内翻式五支点肘杆机构的合模部件。图2为拉杆组件结构简图。拉杆组件是合模部件重要的组成部分，包括拉杆、固定螺母、调模螺母。拉杆两端为螺纹副，固定端为三角螺纹副，拉杆螺母啮合拉杆螺纹并固定于头板（固定模板）；调模端为梯形螺纹副，调模螺母定位于尾板并啮合拉杆螺纹，螺母运动可调节模具厚度。头板固定于底座上，尾板在拉杆组件的作用下做轴向移动。

拉杆在锁模油缸活塞及肘杆机构的力作用下，轴向弹性变形，产生锁模力。锁模机构正常运行，拉杆必须在弹性范围内运行，即在屈服强度区域内运行。拉杆任何部位发生塑性变形，即丧失弹性变形的成型性能，终止寿命周期。

2 拉杆组件的线弹性断裂力学的微裂纹稳定性能的特点的研究

断裂力学认为，一切构件都为微裂纹的弹性体。构件不产生断裂因素的标志的微裂纹稳定。微裂纹稳定指微裂纹尖端应力区域处于正常的弹性力学区域内交变循环运行，无塑性变形，即不发生微裂纹扩展，不能生成诱发断裂的宏观裂纹。微裂纹稳定性能研究是预测和防止拉杆组件断裂的研究重点。微裂纹稳定研究是根据断裂失效件上裂纹的形态、分布、数量、走向、裂纹间的相互位置，确定裂纹产生的先后次序，研究裂纹源位置与应力水平或应力比之间的关系，判断材料失效的模式和原因［1］。

2.1 拉杆组件的裂纹断面特点

拉杆螺纹段断裂失效现象占拉杆组件失效的比例较大，固定端和调模端的螺纹部位都有发生，拉杆螺纹起始处和拉杆螺纹的中间段都有发生。拉杆螺母断裂失效的裂缝出现在螺纹副的首牙与第二牙的牙根，裂缝走向与螺纹升角一致。

断面基本上垂直于拉杆中心线，作用力与裂纹面垂直，属于线弹性断裂力学的张开型裂纹。断面呈金属光泽、未见化学腐蚀痕迹，裂纹扩展区呈放射状。

2.2 拉杆组件的裂纹断裂与微裂纹扩展的分析

微裂纹稳定指构件在弹性范围内运行，未发生塑性变形，更不发生断裂现象，属于线弹性断裂力学。断裂指构件发生塑性变形的宏观断裂，宏观断裂属于弹塑性的非线性断裂力学。

构件的裂纹断裂起始于微裂纹失稳而扩展。从线弹性断裂力学的角度出发，拉杆组件内各金属构件都为微裂纹的弹性体，对于拉杆组件的高强度合金钢，裂纹萌生于夹杂物，在交变应力作用下，这些夹杂物或第二相粒子会与基体沿界面分离或者本身发生断裂，这都可能导致微裂纹的疲劳扩展，这一阶段在整个疲劳寿命中所占的比例高达80%。

构件微裂纹失稳表明外加负载力超过微裂纹弹性变形需要吸收的能量，多余能量用于扩展微裂纹，循环作用下，微裂纹密度增加，刚度下降，失去弹性变形恢复能力，形成宏观裂纹而断裂。外加负载力超过承载能力越大，微裂纹的疲劳扩张速率也越快，断裂疲劳寿命越短。构件进入疲劳断裂阶段，应力应变不在遵守虎克定律。

如果由于表面刻伤，介质腐蚀或原来就存在较大的冶金缺陷（例如铸造球铁），疲劳裂纹生核阶段大为缩短或消失，疲劳断裂越快。

2.3 拉杆组件的交变循环力学特性

交变循环强度是线弹性断裂力学的关键设计参数。同一材料的交变循环强度由交变循环特性决定。如果把构件的力学运行特性搞错，那后续的研究就会失之千里而导向错误。

长期以来，视拉杆组件的交变循环力学运行特征为“拉伸—压缩”非对称循环，并以此作为拉杆组件的强度设计的原则。

拉杆组件的弹性力学运行特性。锁模过程中，油缸活塞的作用力推动肘杆绞支机构，拉杆在肘杆绞支机构的作用下作轴向拉伸弹性变形，应力（力）由零跃升到锁紧位置的最大。制品冷却结束，油缸活塞提供启模力，机构一旦解锁，拉杆瞬间释放在锁模过程中储存的弹性变形能，回复至原状，即拉杆应力由最大恢复到零。

合模机构在锁模过程中，没有对拉杆预压缩，根据能量守恒定律，拉杆弹性恢复不可能产生压缩力，不产生对自身的压缩而产生负应力。可见，拉杆在正应力与零应力之间脉动载荷循环运行，而不是在拉伸—压缩的正—负的应力之间交变载荷的循环运行。图3反映了拉杆组件的交变循环力学运行特征为“拉伸—零”脉动循环［2］，即循环特征系数为-1。

图3 拉杆组件脉动循环的运动特征图

3 拉杆组件的线弹性断裂力学的微裂纹稳定的技术内涵及应用理论的研究

拉杆组件的线弹性断裂力学的微裂纹稳定的技术内涵包括微裂纹稳定的强度判据、微裂纹稳定的三要素两个部分。

3.1 拉杆组件的线弹性断裂力学的微裂纹稳定的强度判据的应用理论的研究

非线弹性断裂力学衡量构件断裂强度的判据是抗拉应力强度因子。线弹性断裂力学衡量构件微裂纹稳定强度的判据是屈服应力强度因子。应力强度因子表达式与材料的强度相关，高强度的拉杆组件的构件的应力强度因子K1的表达式：

式中：

K1——应力强度因子，可理解为负载应力强度因子；

C——裂纹形状因子，一定的构件为常数项。通常在1～2之间。对半径为a1的内部的圆片形裂纹，。对工程中常见的半椭圆形表面裂纹，裂纹深度a1与长度之比为0.1～0.3时，；小于0.1时，C≈2。高强度构件，C=2。

σ——作用在裂纹净断面上的负载应力极限；

a1——微裂纹初始尺寸之半。

式（1）反映了，微裂纹稳定情况下，应力强度因子随应力的增大而增大，它的大小决定了应力场的强弱。

微裂纹稳定的极限应力强度因子K1c：

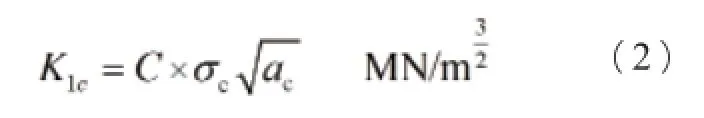
式中：

Ac——构件微裂纹稳定的极限尺寸；

σc——微裂纹稳定的极限屈服应力；

K1c——微裂纹稳定的极限屈服应力强度因子，表征构件抗微裂纹扩展的能力。一定构件的同一部位，都有一个恒定的参数。

利用（2）式各量之间的关系，若已知微裂纹稳定的极限屈服应力σc，以及材料的K1c、Y，就能确定微裂纹稳定的极限临界尺寸ac的大小；若已知Y，微裂纹稳定的极限尺寸ac，以及K1c，就能确定有微裂纹稳定的极限屈服应力σc。

式（2）表明，微裂纹稳定尺寸越大，稳定时极限应力就越小，反之亦然。这也说明了，锻打的材料，由于材料致密，微裂纹尺寸小，屈服强度高，应力强度因子大，抗拉断性能优；铸件疏松，微裂纹尺寸大，屈服强度低，应力强度因子小，抗拉断性能差。在外加应力一定的情况下，若微裂纹尺寸越大，应力强度因子越大，即表示构件越危险；在微裂纹尺寸一定的情况下，若外加应力越大，则应力强度因子也越大，即构件也越危险。

Irwin理论认为，裂纹扩展的临界状态是裂纹尖端的应力场强度因子达到构件临界强度因子。当外载荷引起的应力在微裂纹尖端大于内聚强度时，微裂纹就会沿晶界扩展，大到足以使微裂纹前端材料分离而迅速失稳扩展时，则可认为达到了微裂纹失稳临界状态。在此基础上建立微裂纹的稳定判据：

K1c是K1的临界值。如果K1低于K1c，裂纹并不会快速失稳扩张；只有当K1增至K1c时，微裂纹失稳扩张才能发生。要正确运用断裂判据式，就必须决定构件在裂纹尖端附近的应力强度因子K1，以及构件的K1c。

为保证拉杆组件载微裂纹稳定状况下可靠地脉动循环运行，定义一个脉动循环应力强度因子K1u，根据式（2）的原理，脉动循环屈服应力强度因子K1u:

式中：

σu——临界脉动循环屈服强度。

脉动循环应力强度因子K1u应具有可靠的安全系数均值和承载能力综合系数k，才能确保微裂纹初始尺寸稳定，为此定义一个许用屈服应力强度因子［K1u］：

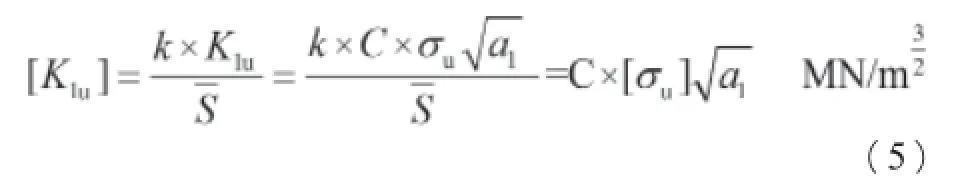
式中：

k——承载能力的综合系数，考虑到引起构件晶体的不完整性的大大降低疲劳强度的宏观因素（如裂纹、缺口、高应变区、应力集中等），通过一些技术措施提高微裂纹的稳定能力及性能。

［σu］——许用脉动循环屈服强度极限：

脉动循环运行的安全运行的微裂纹稳定判据：

3.1.1 同一构件同一部位的微裂纹稳定的应力强度因子的判据理论研究

同一构件同一部位，C、a、σu及安全系数均值和承载能力的综合系数均相同，由式（1）、（5）、（7），微裂纹稳定的应力强度因子的判据归结为应力判据：

式（8）的应力判据有别于传统的许用强度，许用脉动循环屈服强度［σu］，体现出微裂纹稳定的量化安全性评价的疲劳寿命系数的安全系数均值，并且还包括体现出设计中对构件材料进行选择，对构件工艺进行容限设计的承载能力的综合系数。

3.1.2 同一构件不同部位的微裂纹稳定的应力强度因子的卸载性能的判据理论研究

卸载理论运用于同一构件的相邻部位的负载能力设计。拉杆组件的同一构件不同部位指拉杆构件的固定端的卸载段A和固定螺纹段、调模端的卸载段C和调模螺纹段的两个相邻的两个部位。拉杆的断裂设计就是科学地解决螺纹段的断裂问题。

卸载性能判据。传统的卸载性能判据把应力卸载作为唯一的判据，反映在拉杆卸载性能设计上，把卸载段的设计作为应力卸载槽设计，认为卸载段的应力大于螺纹段的应力，就能达到螺纹段不发生断裂。事实上，虽然卸载段的负载应力大于螺纹段的负载应力，仍未能从根本上解决螺纹段的断裂问题。从线弹性断裂力学可很好解释这个问题。如果两者各自的应力强度因子不符合3.1.1节的判据，受到额定负载后，各自处于塑性变形，微裂纹失稳进入扩张断裂阶段，不再遵守应力于应变成正比关系的虎克定律。螺纹段的表面质量及结构均差于卸载段，微裂纹一旦扩展，底径表面部分微裂纹密度扩展率高，吸收能量率高，应力强度因子增速率快，导致微裂纹快速失稳，快速形成主裂纹，当大于卸载段的应力强度因子，发生疲劳断裂，即所称的低应力断裂。卸载段表面质量系数好，抗微裂纹扩展能力高，应力强度因子增速率低于卸载段。

卸载功能主要是降低螺纹段的晶粒单位的吸收能量，达到降低向晶粒边界扩展的动能，稳定微裂纹的弹性变形能力，不使螺纹段的微裂纹密度增加及尺寸扩展。

卸载段和螺纹段为拉杆不同表面质量的两个部位，在微裂纹稳定条件下，C、a、σu均相同，安全系数均值、承载能力的综合系数不同。

卸载段的应力强度因子大于螺纹段的应力强度因子，微裂纹扩展首先发生在卸载段，由于卸载段的抗微裂纹扩展能力高，裂纹疲劳寿命系数高，起到对螺纹段的微裂纹稳定的保护作用。

根据以上分析，作者根据微裂纹稳定的应力强度因子条件，结合弹性力学、经典力学、疲劳力学及可靠性设计，提出以下的卸载段与螺纹段的线弹性断裂力学的判据：

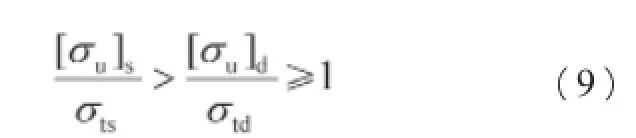
式中：

［σu］d——卸载段的许用脉动屈服强度极限；

［σu］s——螺纹段的许用脉动屈服强度极限；

σtd——卸载段负载应力极限；

Ad——卸载段截面积；

σts——螺纹段负载应力极限；

As——螺纹段螺纹根部的截面积。

式（9）的同一构件不同部位的微裂纹稳定的应力强度因子的卸载性能的判据，突出了相邻部位本身必须达到式（6）的微裂纹稳定的应力强度因子的判据要求，才能达到螺纹段不发生断裂的卸载性能。

3.2 拉杆组件线弹性断裂力学的微裂纹稳定的三要素的应用理论的研究

式（6）表明，拉杆组件线弹性断裂力学要素主要包括安全系数均值、脉动循环屈服强度极限、承载能力的综合系数等三要素。

根据拉杆组件的脉动循环特性，科学确立安全系数均值、承载能力的综合系数、脉动循环屈服强度极限的微裂纹稳定的线弹性断裂力学的工业设计理论，才能有效预测和防止拉杆组件的微裂纹扩张而断裂的概率。

传统的拉杆组件的设计多数采用类比法，同一锁模力规格的拉杆的主体直径的差别为5 mm，但是断裂的概率确相差很大，主要原因是对拉杆组件的断裂力学的特性缺乏研究，更不知关键设计元素的确定和应用。例如卸载槽断裂，理解为直径太小，做加大处理，结果越加大，断裂概率越高。

3.2.1 拉杆组件的线弹性断裂力学的微裂纹稳定的安全系数均值的应用理论的研究

安全系数均值是拉杆组件线弹性断裂力学的三要素之一。

基于线弹性断裂力学的安全系数均值，微裂纹稳定的弹性力学范畴内运行的可靠性的安全系数均值，进一步突出了安全系数均值的使用范畴。

线弹性断裂力学的安全系数均值体现出了微裂纹稳定的“量化”寿命周期的特征。

3.2.1.1 线弹性断裂力学的微裂纹稳定的安全系数均值的工程理论

传统的安全设计和选材的注意力集中于增大强度安全储备量，然而这往往会降低材料的韧性，增加脆断的危险。可靠性安全系数均值实现了传统的安全系数的量化性、内涵性，更能精确反映出拉杆组件的微裂纹稳定的寿命系数，提高其绿色化制造的技术含量。

拉杆承载L的值和负载P的值都是属于统计性质的，并且一般符合正态分布或韦伯分布，故可用正态分布函数来求满足指定可靠度下的安全系数的最小值。

拉杆承载能力的正态分布概率密度为：

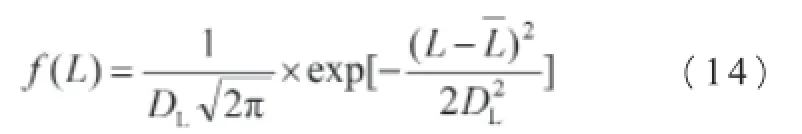
式中：

L——拉杆承载；

DL——拉杆承载的标准离差。

拉杆负载的正态分布概率密度为：

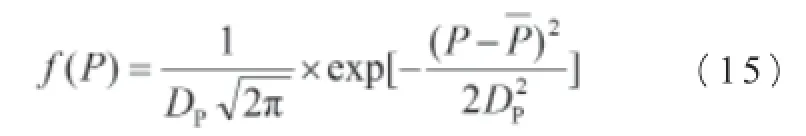
式中：

P——拉杆负载；

DP——拉杆负载的标准离差。

保证拉杆组件的微裂纹稳定的正常运行的条件是：

L和P都是符合正态分布的随机变量，可知δ也是一个符合正态分布的随机变量，且它也具有均值与标准离差：

δ正态分布概率密度为：

式（16）、（17）、（18）代入上式，δ正态分布概率密度为：

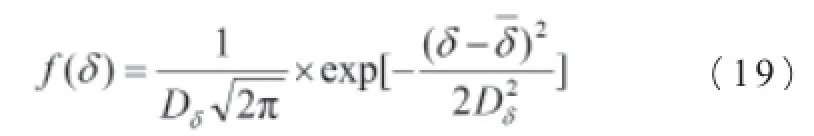
图3中隐形区为P可能大于L的重叠区，表示P与L发生干涉，引起失效，但该区面积并不定量表示失效概率的大小：当P＞L，两者发生干涉而失效；P＜L，虽然两者压阴影区，但不发生失效。图4的阴形面积表示失效概率的大小，如令可靠度为R（t），则失效概率：

图4 L、P分布函数以及相互件的关系

为便于数字上处理，令联结系数Z：

Z的标准离差DZ=1，正态分布概率密度为：

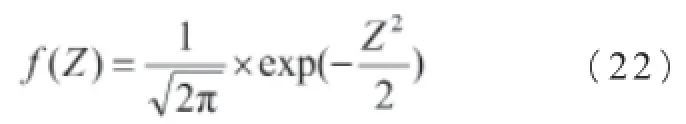
失效概率的正态分布概率密度为：

为便于运算和数学处理，工程设计中将标准正态分布面积表中的Z与R（t）的联结关系，作回归分析法，可求出Z与Q的近似关系式，联结系数：

上述关系式，在0.999＞R（t）＞0.985范围内，误差在3%之内，已符合工程设计要求。

图5 联结系数Z的分布函数

合并式（24）、（25），可得安全系数均值：

承载标准离差：

负载标准离差：

式中：

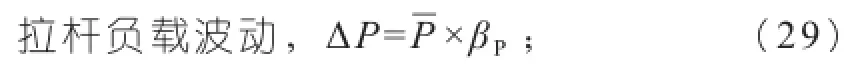
拉杆负载波动系数，指由于机构特点、装配精度等造成四根拉杆之间、同一拉杆对称点之间所受载荷不一致。表1为某一注塑机四根拉杆负载的应变测试值，负载波动为0.06～0.18。载荷波动系数取βP=0.20，较能反映负载波动实际工况；

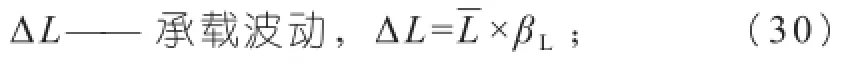
βL——承载能力波动系数。真实的材料构件由于冶金及加工因素（热处理硬度波动、热处理质量波动、晶粒大小、微裂纹尺寸及密度等），破坏了经典力学中材料是均匀、连续、各向同性的基本假设，承载能力必须考虑到这些因素的存在及波动。

图6为承载L和负载P关系图，可得：

表1 拉杆负载应变测试值

拉杆负载极限最小值：

拉杆负载最大值：

拉杆承载能力极限最小值：

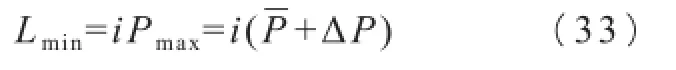
式中:

i——超载系数，一般取1.25。

承载能力最大值：

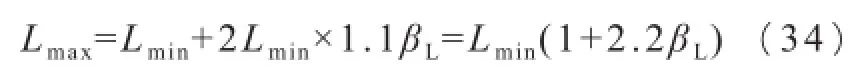
承载能力均值：

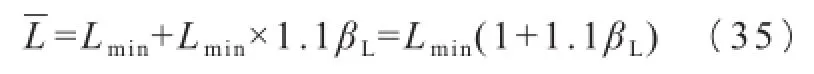
由3.1节线弹性断裂力学的分析，微裂纹失稳进入扩张断裂阶段，当L＞P，仍然发生低应力断裂。传统的可靠性安全系数均值仅适用于线弹性断裂力学的微裂纹稳定的运行状况，一旦微裂纹失稳，传统的可靠性安全系数均值不再适用于许用应力强度因子的判据参数。

3.2.1.2 线弹性断裂力学的微裂纹稳定的安全系数均值的工业设计实例

例1：额定锁模力Pm=1 500 kN的双曲肘斜排列合模机构的注塑机，负载波动系数βP=±0.2。拉杆材料为42CrMo，热处理为T HB280，调质波动范围标准为±15HB，波动系数βT=±15/280=±0.054。42CrMo，调质均匀度波动系数βY=±0.05；材料质量波动系数βZ=0.10；螺纹表面粗糙度Ra1.6，粗糙度的波动系数βE=±0.05/0.85=±0.06。拉杆表面氮化，质量系数βσ=1.25。根据使用要求，拉杆的可靠度R为0.999，即失效概率Q不大于0.001。承载能力超载系数1.25，波动系数βL=±0.2。拉杆组为四组。确定拉杆安全系数均值。

图6 承载L和载荷P关系图

由对拉杆承载能力的波动系数分析，可以看出，拉杆主体段与螺纹段的波动系数的项目不同，所以安全系数的均值也有差别。

由以上已知参数，单根拉杆额定负载均值：

由式（27），负载波动：

由式（28），负载离差：

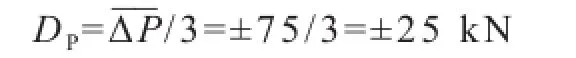
（1）拉杆光轴段安全系数均值

拉杆光轴段承载能力波动系数：

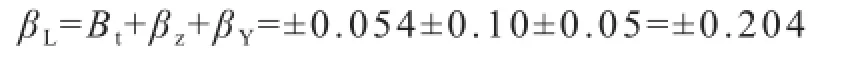
由式（33），承载能力极限最小值：

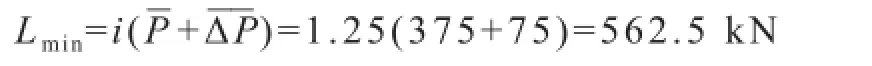
由式（34），承载能力最大值：

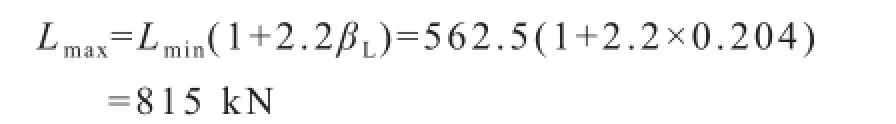
由式（35），承载能力均值：

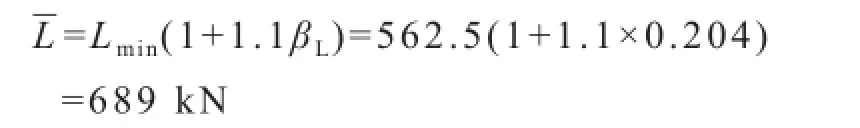
由式（30），承载波动：

由式（27），承载离差：

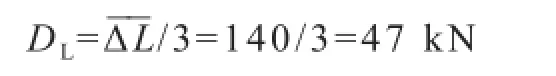
（2）拉杆螺纹段安全系数均值

拉杆螺纹段承载能力波动系数：

由式（27）：

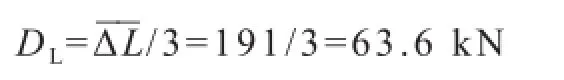
将以上数值代入式（26），拉杆螺纹段及拉杆螺母的安全系数均值：

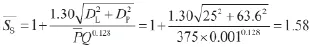
例1的安全系数均值计算取得的两个均值，符合资料［3］推荐的构件在交变应力作用下，力的确定精度一般，材料均质性适度，强度储备系数1.4～1.7的原则。但本节从可靠度方面研究得出的安全系数均值，达到较为精确的“定量”，而不是传统的“定性”，具有明显的科技进步意义。

3.2.1.3 线弹性断裂力学的微裂纹稳定的安全系数均值诸因素的分析研究

式（13）反映了承载和负载的离差决定了安全系数的均值，波动系数对安全系数的均值具有决定性的核心。加强质量控制，使波动系数在控制范围内，才能确保安全系数均值在实际应用中的真实性。

负载波动系数与零件的加工的形位公差、装配精度、设计的公差配合的选择等因素直接相关。拉杆之间、同一拉杆各部位之间，负载波动20%为正常波动，但有的注塑机的拉杆负载波动达到40%， 大幅缩短了寿命周期。例1中，如负载波动系数为0.4，其余波动系数不变，则安全系数为1.58。安全系数均值的增大，给后续设计带来一系列的问题。

承载波动系数主要与热处理的波动相关。调质波动指宏观的控制，匀度波动指微观控制，匀度控制更具有重要性，例如有的拉杆断裂的截面，晶粒细度不匀，属于非正常断裂，而是匀度波动太大。

3.2.2 拉杆组件的线弹性断裂力学的微裂纹稳定的脉动循环屈服强度要素的应用理论的研究

脉动循环屈服强度设计是拉杆组件线弹性断裂力学的微裂纹稳定的三要素之一。

节3.1分析表明，拉杆组件的微裂纹稳定的强度的判据为脉动循环屈服极限。

3.2.2.1 拉杆组件脉动循环屈服强度

脉动循环屈服强度基于对称循环屈服强度。作者根据有关资料及实际应用效果，在对称循环屈服强度基础上，总结出两者之间的关联度，确立脉动循环屈服强度。

运用沃勒公式确定对称循环屈服强度：

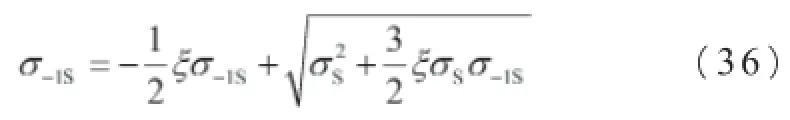
式中：

σ-1S——对称循环屈服强度，MPa；

σs——静负载的屈服拉伸强度，MPa；

ξ——对称特征系数，ξ=-1。

ξ=-1代入式（36），整理后，对称循环屈服强度近似为：

同理，对称循环抗拉强度：

强度直接与热处理参数相关，虽然是个机械设计的常识，但在工程设计中发现往往把强度与热处理参数直接的联系孤立起来，零件图上随心所欲写上一个热处理参数，而在确定强度参数也欠有力的理论根据。经作者统计，推荐以下热处理参数之间及与抗拉强度σb之间的折算：

（1）热处理硬度与抗拉强度σb之间的换算：

1RC=32 MPa；1HB=3.5 MPa

（2）热处理硬度之间换算：

1RC=9.5 HV；1RC =9.2 HB

（3）抗拉强度与屈服强度之间的换算

式（37）中，较为精确确定σS，是确定σ-1S的前提。

拉杆为40Cr/42CrMo，屈服强度：

QT500-7球墨铸铁的屈服强度：

脉动屈服循环强度与对称屈服循环强度之间的关联。脉动循环强度与对称循环强度有所不同，主要取决于材料的瞬时敏感系数，根据资料［3］及式（37），对拉杆及拉杆螺母的脉动循环强度提出以下折算关系：

拉杆构件的脉动循环屈服强度：

拉杆构件的脉动循环剪切强度：

球墨铸铁螺母构件的脉动循环屈服强度：

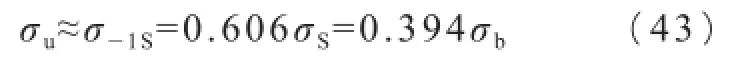
球墨铸铁螺母构件的脉动循环剪切强度：

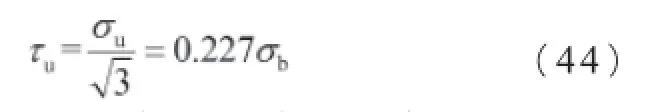
上面把热处理硬度与强度进行关联，上面提高热处理硬度，可提构件的承载能力及断裂力学的性能。

3.2.3 拉杆组件的线弹性断裂力学的微裂纹稳定的承载能力的综合系数的应用理论的研究

微裂纹扩展由表面或近表面处的局部塑性应变集中造成的。通过加工等因素，提高构件的表面质量，使存在微裂纹不发生疲劳扩张或减慢疲劳扩张速率，达到提高承载能力。

承载能力的综合系数k：

κ——有效应力集中系数；

q——材料敏感系数，与材料类别、强度等因数相关。高强度的拉杆材料为应力敏感材料，敏感系数为1。球墨铸铁敏感度低，敏感系数按强度值取0.3。

α——理论应力集中系数，与结构设计相关。公制螺纹取2.06。

βσ——粗糙度的表面质量系数（表2）。粗糙度高，有利于降低表面微裂纹密度及长度，使存在微裂纹不发生疲劳扩张或减慢疲劳扩张速率。

表2 粗糙度的表面质量系数

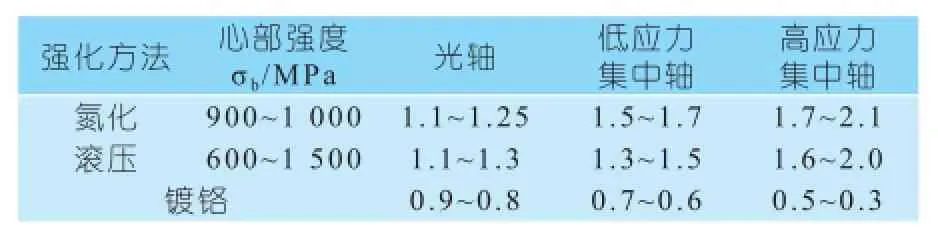
表3 强化方法的表面质量系数

βq——表面强化系数（表3），与强化型式及强化参数相关，表面强化可有效提高构件的屈服强度。过去认为只有提高硬度以防止塑性形变才能提高疲劳限。断裂力学根据微裂纹的疲劳扩张和会合，提高构件表层的压应力可获得高疲劳强度和寿命。表面强化工艺（如表而淬火、渗炭、喷丸）就是为了造成构件表层压应力层， 获得高疲劳强度和寿命。表3中，硬度高，表面强化系数去大值。

βc——尺寸系数（图7）；

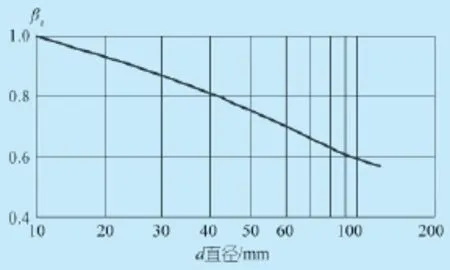
图7 尺寸系数与直径之间的关联图

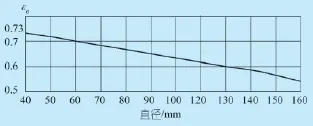
图8 合金钢尺寸弯矩系数与直径之间的关联图

εσ——尺寸弯矩系数，与截面直径相关（图8）。综合系数根据实际对象及力学性能取舍。提高许用脉动循环屈服强度的关键是提高质量系数，表面强化处理是提高质量系数最有效的技术措施，例如，表面滚压、氮化可达2倍的质量系数，也就是可将许用强度极限提高2倍、构件的断裂力学性能得到2倍的增幅。

4 拉杆组件的线弹性断裂力学的微裂纹稳定要素的应用技术的设计研究

国内拉杆螺纹段断裂概率较高，可靠度达不到国家规定的机械行业的0.999可靠度的要求，其主要原因在卸载段的设计上缺乏工业化设计理论的研究。研究卸载段和螺纹段两者的微裂纹稳定性的相互关联的更具科学性、可行性、实用性的设计理论及应用技术，是拉杆组件的重点研究课题。

拉杆主体的主要功能是实现弹性变形达到锁模力；卸载段的主要功能是保证拉杆可靠运行的疲劳寿命周期；螺纹段与螺母联接起到约束拉杆的轴向自由度的功能，实现正常的弹性变形。

4.1 拉杆主体直径的线弹性断裂力学的微裂纹稳定要素的应用技术的设计研究

拉杆制造成本占到合模部件的约20%。减小拉杆主体直径又不影响成型加工性能，是功能化、专用化注塑机的绿色技术的研究重点。线弹性断裂力学的微裂纹稳定的理论拓展了拉杆主体直径的设计理念。

微裂纹稳定理论的拉杆直径极限：

式中：

kL——拉杆主体承载能力的综合系数。

如成型142L的垃圾箱立式专用注塑机，锁模力12 800 kN，四根拉杆，每个拉杆负载3 200 kN，THB320，拉杆主体直径材料42CrMo，直径11 cm，实际运行达到成型性能。普通型锁模力12 800 kN的注塑机的拉杆直径为22 cm。

拉杆抗拉强度：

σb=3.5×320=1 120 MPa

由式（41），脉动循环屈服强度：

σu=0.514σb=0.514×1 120=576 MPa

安全系数均值。专用注塑机的负载波动系数取0.10，承载波动系数取0.20。由3.2.1节原理计算，安全系数均值为S-=1.45。

承载能力的综合系数kL。表面抛光，由表2，粗糙度的表面质量系数为1；表面氮化，由表3，无应力集中，强化的表面质量系数为1.25；直径初算7 cm，由图6，尺寸系数为0.65；主体直径不承受弯矩，弯矩系数为1；有效应力系数为1。由式（45）原理，拉杆主体的承载能力综合系数kL：

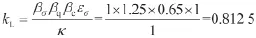
由式（47），拉杆主题直径极限D:

考虑到特殊螺纹的设计，拉杆主体直径实际取11.5 cm。

由式（6），许用脉动循环屈服强度：

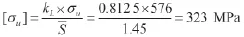
拉杆主体抗拉应力极限及自身应力强度因子的判据：

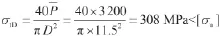
根据式（8）的应力强度因子的判据，符合拉杆微裂纹稳定运行的判据，拉杆不会产生屈服，实际运行证明了弹性变形的可靠性。可见，运用线弹性断裂力学的微裂纹稳定的设计理论，拉杆主题直径从22 cm减小到11.5 cm，充分体现了节约资源、节能降耗的绿色设计理念。企业降低了制造成本，用户降低了投资成本，社会降低了二氧化碳的排放量，三方都提高了效益。

4.2 拉杆固定端的线弹性断裂力学的微裂纹稳定要素的的应用技术的设计研究

拉杆固定端包括卸载段A和固定螺纹段两个部分，图9为拉杆固定端的结构简图。

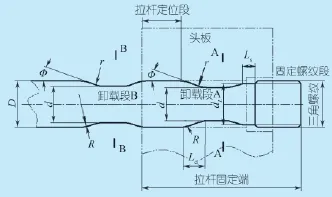
图9 拉杆固定端的结构简图

4.2.1 拉杆固定端的受力分析

由图9，拉杆与头板的联接分为定位和非定位两个部分，非定位部分是拉杆与头板拉杆孔相对于定位部分具有较大的活动空间，卸载段容许承受一定的弯矩，弯曲变形产生在卸载段，A-A为应力强度因子最大的截面。

图10为拉杆固定端的锁紧状况下的受力简图。肘杆机构负载锁紧，头板中心区域绕曲，拉杆不可能达到理想的中心负载，而是偏心负载，处于拉伸和弯曲的复合负载。

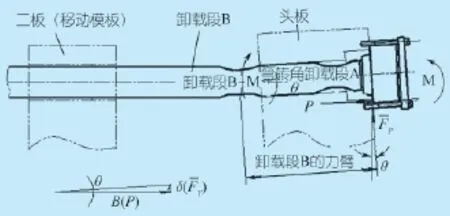
图10 拉杆固定端的锁紧状况下的受力简图

轴向力：

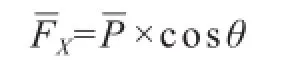
式中：

θ——偏心角，

δ——头板绕度；

B——二分之一拉杆中心距。

4.2.2 拉杆卸载段A的线弹性断裂力学的微裂纹稳定要素的设计研究

4.2.2.1 卸载段A的应力分析

根据受力型式，卸载段A的负载应力为抗拉和抗剪的复合应力。

抗拉应力：

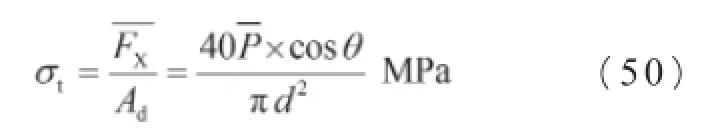
抗剪应力：

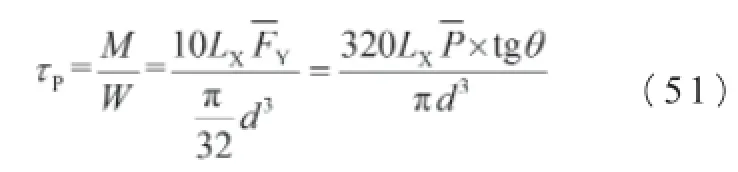
式中：

d——卸载段直径；

LX——力臂。

卸载段负载应力：

4.2.2.2 卸载段A直径

卸载段直径极限d：

式中：

k1——卸载段A的承载能力的综合系数。

式（49）得出的结论为极限值，非最终的设计值。

4.2.2.3 卸载段A的线弹性断裂力学的微裂纹稳定的直径设计及应力强度因子校核的举例

以例1为例：拉杆材料42CrMo，THB280，头板绕度δ=0.012 mm，对卸载段A的力臂LX=15 cm。

由3.2.1，抗拉强度：

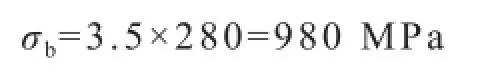
由式（41），脉动循环屈服强度：

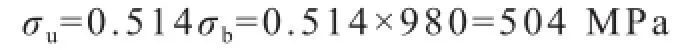
拉杆为合金钢，材料敏感系数趋近于1；卸载段理论应力集中系数趋近于1。由式（46），卸载段有效应力集中系数：

卸载段A承载能力综合系数k1。表面抛光，由表2，粗糙度的表面质量系数为1；表面氮化，由表3，无应力集中，强化的表面质量系数为1.25；直径初算5 cm，由图6，尺寸系数为0.75；承受一定的弯矩，由图7，直径5 cm的弯曲系数为0.71；有效应力系数为1。由式（45），卸载段A的承载能力综合系数k1：

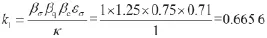
由式（53），卸载段A的直径极限d：

卸载段A直径初定为4.6 cm。

由式（49），偏心角：

由式（51），抗剪应力：

由式（50），卸载段A的抗拉应力极限：

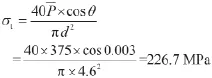
由式（52），卸载段A复合应力：

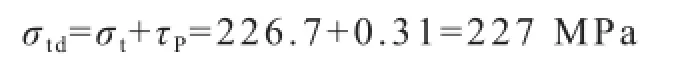
由式（10），卸载段A的应力强度因子的许用脉动循环抗拉强度及自身应力强度因子的判据：

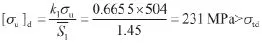
符合式（8）的判据，卸载段A不会发生微裂纹失稳，能在正常的弹性范围内运行。

例1的分析，说明卸载段A的抗剪应力很小，相对于抗拉应力可忽略不计，按式（50）计算σtd=226.7 MPa，完全达到工业设计的精度要求，所以在工业设计中按式（50）计算卸载段的负载应力。

4.2.3 拉杆固定端的螺纹段的线弹性断裂力学的微裂纹稳定要素的的应用技术的设计研究

拉杆疲劳断裂都发在螺纹段。拉杆的螺纹为高应力集中处。

4.2.3.1 承载能力与螺距

螺距与齿厚直接相关，螺距大，螺纹中径处厚度也大，有利于提高承载能力。为达到最大的承载能力，在许可条件下，尽量增大牙距。但螺距受到螺纹自锁性能的限制，不能无限增大。

螺纹升角应满足：

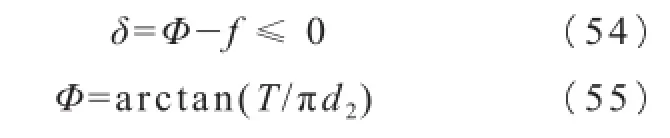
当量摩擦系角 ：

式中：

T——螺距，增大螺距，有利于降低螺纹底部应力集中系数；

α——牙型角；

μ——螺纹间摩擦系数，调模螺纹副，粗糙度0.4～0.8，一般取μ=0.01。

以螺纹M200为例，螺距为T=4，Φ=0.36；螺纹角为60°，当量摩擦角为0.66，δ=0.36-0.66=-0.30＜0。如螺距为T=8，Φ=0.73；螺纹角为60°，δ=0.73-0.66=0.07＞0，不符合自锁性能要求。

4.2.3.2 拉杆螺纹底径的脉动循环屈服强度的设计研究

拉杆螺纹脉动循环强度极限以脉动循环屈服拉伸强度极限为基准参数。拉杆螺纹是拉杆的一部分，螺纹公称外径不大于拉杆主体直径D。

4.2.3.2.1 拉杆螺纹的承载能力综合系数

拉杆螺纹承载能力综合系数包括粗糙度的表面质量系数、强化方法的表面质量系数、尺寸系数以及有效应力集中系数，不含弯矩系数，根据式（46）的原则，拉杆螺纹的承载能力综合系数k2：

4.2.3.2.2 拉杆螺纹底径极限d1

拉杆螺纹底径极限k1：

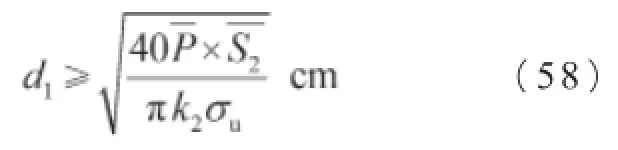
式中：

k2——螺纹段的承载能力的综合系数。

式（58）得出的结论为拉杆螺纹底径极限值，非最终设计值。根据拉杆结构实际，偏转力矩能力校核等后，才能最终确定。如果计算结果大于拉杆主体直径，则应提高承载能力的综合系数，主要提高表面质量系数，达到降低螺纹底径。

Reseach and application on microcracks stable element of injection molding machine rod assembly based on linear elastic fracture mechanics (Part 1))

Research and application on microcracks stable element of injection molding machine rod assembly based on linear elastic fracture mechanics (Part 1)

Zhang Yougen, Cao Liang
(Ningbo Haida Plastic Machinery Co., Ltd., Ningbo 315200, Zhejiang, China)

Based on the microcracks theory of linear elastic fracture mechanics, the article analyzes the association between microcracks stability factors and fracture of the injection molding machine rod assembly. The article corrects traditional unsymmetrical cyclic movement mechanics characteristic of the rod assembly, and fi rst proposes a new viewpoint of pulsation cyclic elasticity motion characteristics of the rod assembly, laying a theoretical foundation for the scientifi c use of microcracks stability tress intensity factor theory. The article creates a criterion theory of microcracks stability stress intensity factor, explains the mechanic factors of rod fracture, and provides the theoretical design basis of microcracks stability of performance unload. With examples, the article proposes industrial design theory and application principles of three elements, such as reliability safety factor mean value, integrated coeffi cient of carrying capacity and pulsation cycle yield strength, presents design theory and determine principles of unload section diameter, threaded section bottom diameter and rod nut. The article studies the link among linear elastic fracture mechanical elements, elastic properties and quality control, explores quality elements R & D direction for increasing microcracks stability. The article uses innovative industrial design theory of linear elastic fracture mechanics elements of rod assemblies, to analysis fracture failure examples, and the article further describes that research of microcracks instability of linear elastic fracture mechanics factors is helpful to predict and prevent fractures of rod assemblies.

injection molding machine; rod assembly; linear elastic fracture mechanics; research; application

TQ320.5

1009-797X（2015）06-0006-14

B

10.13520/j.cnki.rpte.2015.06.002

（未完待续）

张友根，男，教授级高级工程师，终生享受国务院政府特殊津贴，现主要从事塑料机械的科学发展工作。

2014-03-14