坡膛结构参数对枪械内弹道挤进时期的影响研究

陆野，周克栋，赫雷，李峻松，黄雪鹰

（1.南京理工大学机械工程学院，江苏南京210094；2.中国兵器工业第208研究所，北京102202；3.63856部队，吉林白城137001）

坡膛结构参数对枪械内弹道挤进时期的影响研究

陆野1，周克栋1，赫雷1，李峻松2，黄雪鹰3

（1.南京理工大学机械工程学院，江苏南京210094；2.中国兵器工业第208研究所，北京102202；3.63856部队，吉林白城137001）

枪械射击过程中枪管坡膛处工作环境恶劣，为了研究枪管坡膛角度对挤进过程坡膛处受力的影响，建立了不同坡膛角下考虑枪管及弹头结构特性、本构非线性等因素的三维有限元模型，分析了不同坡膛角对弹头挤进过程的影响，获得了不同坡膛角下挤进阻力随挤进位移的变化数据；建立了挤进阻力的响应面模型，基于上述数据采用Hermite多项式，求解获得了挤进阻力以坡膛角和挤进位移为变量的计算公式；提出建立了考虑挤进阻力的弹头挤进过程的动力学模型，编程计算了枪弹挤进过程中的挤进压力，获得了某大口径机枪满足弹头初速条件的坡膛角度取值范围为0.11°～1.13°，进而得到了缓减枪管坡膛受力、保证弹头最高初速、满足坡膛角设计范围的坡膛角度最优解为0.56°。

兵器科学与技术；枪管；弹头挤进；坡膛；接触；冲击

0 引言

自动武器在连发射击过程中，枪管经历着火药燃气高温、高压、弹头高速、高加速度的高频热压耦合冲击、机械冲击等作用，这种工况严重影响了枪管寿命。实践表明，枪管坡膛处工作环境最恶劣，最容易先发生破坏［1］。目前，我国自动武器寿命偏低已成为制约我国新一代枪械性能提高的瓶颈问题。实际工况下的自动武器弹头挤进以及内弹道过程很难通过实验来得到准确的数据，而弹头挤进过程又是影响枪管寿命的主要因素之一。目前，关于自动武器弹头挤进过程的国内外的研究报道还不是很多。文献［2-4］对弹头挤进过程进行了初步的分析与研究，但均未涉及弹头挤进过程中膛线压痕的形成过程及变形特点。文献［5］建立了弹头挤进枪管的有限元分析模型，通过数值模拟研究了铅芯弹头的挤进过程，展示了弹头上膛线压痕的形成过程和材料的流动情况，分析了挤进前后弹头壳和铅芯的变形特征，以及挤进结束后弹头的残余应力。文献［6］建立了弹带材料基于连续介质损伤力学的本构模型，同时考虑了经典内弹道方程组和弹带挤进过程的耦合效应，对两种坡膛结构下弹带挤进过程进行了数值模拟。上述研究均进行了三维数值仿真分析，但并没有考虑弹头实际内部结构对仿真结果的影响，同时也没有对挤进阻力、挤进压力等挤进参数随枪管内膛结构参数变化的规律进行相应的分析。本文针对某大口径机枪的挤进内弹道时期，构建了枪弹挤进过程中的高冲击、强摩擦和大变形接触下的有限元模型，模拟了弹头的挤进过程，分析了6种不同坡膛结构对弹头挤进过程的影响，解算了挤进阻力以坡膛角和挤进位移为变量的计算公式；通过建立考虑挤进阻力的弹头挤进过程动力学模型，计算了变容状态下枪弹挤进过程中的膛内火药燃气平均压力，分析了弹头初速随挤进压力、挤进压力随坡膛角的变化规律，获得了满足弹头初速条件的挤进压力与坡膛角度取值范围，进而得到了缓减枪管坡膛受力、保证弹头最高初速、满足坡膛角设计范围的坡膛角度最优解。研究结果对提高枪管寿命具有一定的指导意义。

1 枪弹挤进阻力理论分析

枪弹挤进过程中，弹头受到枪管坡膛、阴线和导转侧的作用力，分别为坡膛阻力Fc，阴线阻力Fs和导转阻力Fd，这三部分的合力构成了挤进阻力F.对挤进过程弹头受力分析如图1所示，其中η为缠角，β为坡膛角，α为导转侧角度。

令在接触面上产生的接触应力分别为:σc、子c，σs、子s和σd、子d，其中法向应力和切向应力通过摩擦系数υ呈比例关系，即

图1 挤进过程弹头受力分析图Fig.1 Mechanical analysis of projectile during engraving

由此可得沿弹轴方向的挤进阻力分别为

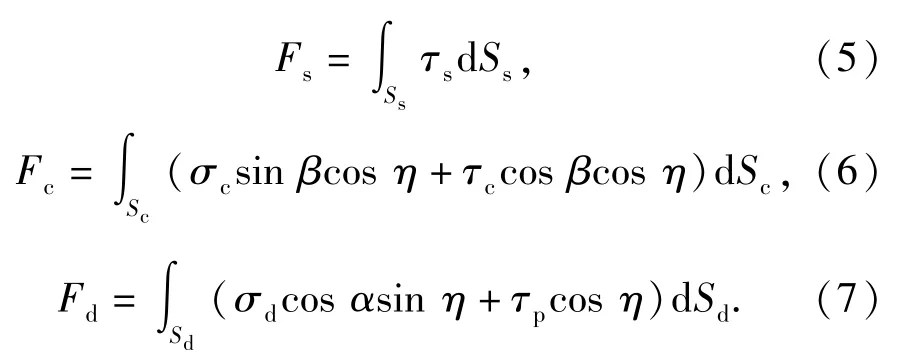
弹头挤进膛线的过程时间极短，挤进结束后弹头所获得的速度非常小，弹头挤进过程弹头和坡膛的摩擦特性变化很小，可认为摩擦系数υ不变，由上述理论分析可知，在其余参数一定的情况下，挤进阻力仅与坡膛角和挤进位移有关。为了更加直观地表述挤进阻力与坡膛角和挤进位移的数值关系，本文通过高精度有限元仿真获得挤进阻力与坡膛角的对应数据，采用随机响应面法建立挤进阻力与坡膛角及挤进位移的代理模型，计算挤进阻力随坡膛角及挤进位移变化的函数表达式。

2 挤进过程有限元分析

2.1 有限元模型的建立

本文以某大口径机枪枪管及弹头为对象，枪管壁厚、膛线，弹头内部等保持实际结构，如图2所示，考虑弹头的柔性效应，采用有限元前处理软件Hypermesh分别对枪管、弹头主体和弹带划分网格，并对关键部位进行精细化处理，如图3所示。

图2 枪管与弹头的三维实体模型Fig.2 3D solid model of barrel and projectile

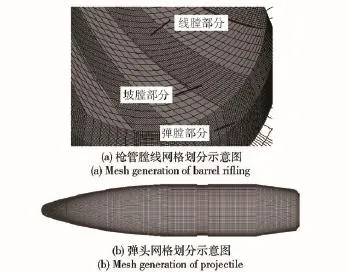
图3 枪管与弹头的有限元模型Fig.3 Finite element models of barrel and projectile

2.2 加载与求解

由击发底火到弹头全部嵌入膛线的过程称为挤进膛线时期，此过程由于弹头移动量不大，可近似认为火药定容燃烧，引用火药气体定容燃烧状态方程为

式中:f为火药力；Δ为装填密度；ψ为火药已燃烧的相对质量；δm为火药密度；α为余容；pB为点火药压力。

引用燃气生成方程与燃烧速度方程为

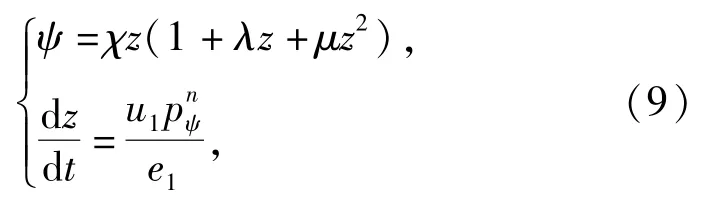
式中:z为火药已燃烧的相对厚度；n为燃速指数；u1为燃速系数；e1为火药原厚度；χ、λ、μ均为药形系数。

联立方程（8）式、（9）式，代入某大口径枪弹的火药特性参数，通过MATLAB编程即可计算出挤进膛线时期的弹底压力曲线施加于弹头尾端面，即为力边界条件。设置枪管楔形凹槽处为固定约束，该条件为位移边界条件。

本有限元模型应用Johoson-Cook材料本构关系［7］，采用适用于求解复杂的非线性、大变形的显式动力学问题的显式非线性求解器LS-DYNA进行计算，针对挤进过程的特征，采用自动接触模型算法，设置罚函数因子保持接触界面的协调性；考虑到弹头挤进过程中可能出现网格畸变现象，在计算过程中采用ALE自适应网格技术，确保计算的精度及效率。

为确保弹头挤进过程的响应面代理模型的准确性，本文基于现有枪管坡膛角的设计范围，建立了6种不同坡膛角（如表1所示）的有限元模型，分别进行了仿真分析。针对弹头被甲的变形与膛线刻痕的形成情况和挤进过程挤进阻力的变化情况，使用后处理软件Ls-Prepost，对仿真计算的数据进行整理分析。

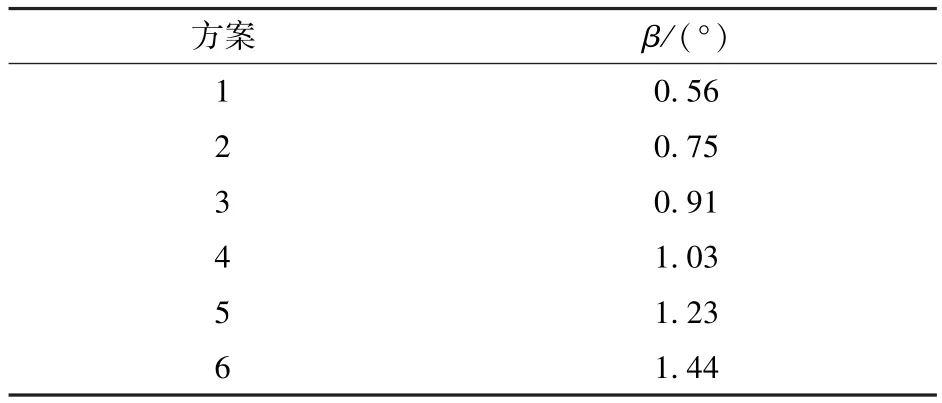
表1 6种不同方案坡膛角度列表Tab.1 Forcing cone angles of six different schemes

3 枪弹挤进过程代理模型的建立

本文采用随机响应面法构建弹头挤进过程的代理模型［8］。目前常用的数据拟合方法有Gauss法、Sina法、Lorentz法、Voigt法、Hermite法等，其中前面4种方法适用于单变量数据的拟合，而Hermite多项式法可用于多个变量数据的拟合，拟合精度高。本文基于有限元仿真获得了不同坡膛角及挤进位移两个变量的挤进阻力的变化数据，故采用Hermite多项式编写MATLAB程序求解挤进阻力以坡膛角和挤进位移为变量的计算公式，分析挤进阻力的变化规律。输出响应量H采用如下Hermite多项式展开来表示:

式中:a0、ai1、ai1i2等为待定系数；xi1，xi2，…，xin为独立的变量；q为变量的个数；φi为i阶Hermite多项式。本文中输出响应量为挤进阻力F，独立变量为坡膛角β和挤进位移x.

确定（10）式的主要任务是求解待定系数ai1，目前求解待定系数的方法很多，例如配点法、高效配点法和回归法等。Isukkapalli等认为回归法稳健性较好［9］，本文采用逐步回归的方式得到弹头挤进过程的响应面代理模型。

Hermite多项式的递推关系为

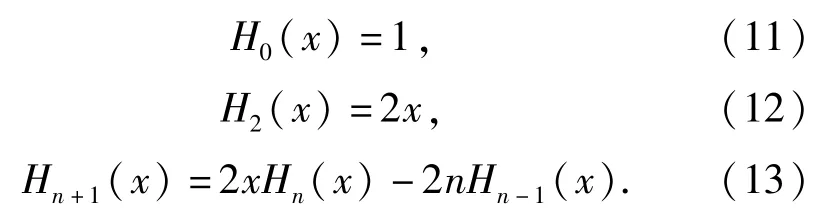
4 挤进过程弹头动力学方程的建立

4.1 挤进压力的影响分析

挤进压力是指弹头全部嵌入膛线受到最大阻力时所对应的膛内火药燃气压力。由于坡膛角的变化会引起挤进过程阻力、时间等参数发生变化，而火药的燃烧对时间极其敏感，从而影响膛内火药燃气压力，使得整个内弹道性能发生变化，因此为保证弹头的初速性能，需要保证挤进压力和坡膛角在一定范围内变化。为有效分析枪弹挤进过程的影响，并提出保证弹头的初速性能，降低挤进阻力峰值的可行方案，本节在随机响应面法建立的枪弹挤进过程的代理模型基础上，结合火药变容燃烧过程和弹头起始动力学过程来分析枪弹挤进动力学过程，建立了考虑挤进阻力的弹头挤进过程动力学模型。

4.2 挤进过程动力学方程的建立

由于经典内弹道方程忽略了弹头挤进膛线的过程，假定弹头全部挤进膛线达到挤进压力时，弹头才开始运动，显然误差较大。本文通过将建立的挤进阻力代理模型与考虑了火药气体变容燃烧和弹头运动过程的经典内弹道方程组耦合，建立了考虑挤进阻力的弹头挤进过程动力学模型，以此来仿真计算膛内火药燃气压力。新建立的枪弹挤进过程动力学方程如下:

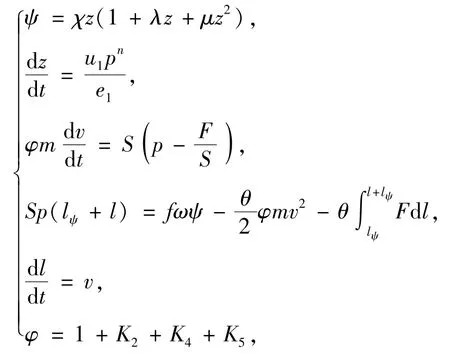
式中:S为身管的等效截面积；u1为正比燃烧定律中的燃速系数；m为弹头质量；p为膛内火药燃气压力；F由枪弹挤进过程的代理模型求解确定；l为弹头行程；lψ为药室自由容积缩径长；f为火药力；ω为装药量；θ=k-1，k为比热比；φ为忽略了挤进阻力所做功的次要功系数，本文中将挤进阻力所做功进行了详细求解，而不是以往采用系数K3进行粗略的估算；K2、K4、K5分别为弹头旋转功、火药气体的运动功和武器后坐部分运动功占主要功的百分比。

5 算例

本文以某大口径机枪的挤进过程为例，进行了建模、仿真与分析。

5.1 弹头被甲膛线刻痕的形成过程分析

为更加直观地反应弹头被甲膛线刻痕的形成过程，取膛线刻痕形成的阶段特征图，按时间顺序展示，如图4所示，随着弹头挤进枪管，弹头被甲膛线刻痕由弹头向弹尾延展，逐渐加深成形。不同坡膛结构下刻痕形成过程、形状基本一致。

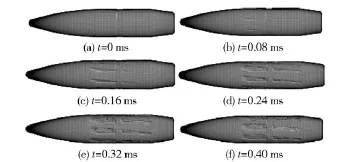
图4 膛线刻痕的形成过程Fig.4 Formation process of rifling indentation

5.2 挤进过程挤进阻力分析

通过对6种不同坡膛角时挤进过程的仿真结果中每个单元所受的阻力进行合成得到挤进阻力随时间及空间变化的规律，如图5、图6所示。由挤进阻力随时间变化图图5可知，随着坡膛角度变大，挤进阻力达到的峰值越大；对所有坡膛角，挤进阻力在达到峰值后逐渐下降并趋于稳定，这是由于挤进阻力包括克服弹头材料变形的力和轴向摩擦力，挤进结束后克服弹头材料变形的力消失，挤进阻力趋于的稳定值为轴向摩擦力；随着坡膛角度变大，挤进阻力达到峰值的时刻越靠前，这是由于随着坡膛角度变大，挤进阻力中克服弹头材料变形的力增大的速率变快，因此挤进阻力达到峰值的时间随坡膛角增大而减少。由挤进阻力随挤进位移变化图图6可知，挤进阻力的峰值随着坡膛角度的增加而增加，弹头与枪管膛线接触后挤进阻力迅速增加，由于弹头中间部位设有阶梯凹槽，因此挤进阻力存在短暂下降阶段。

图5 不同坡膛角时挤进阻力随时间变化图Fig.5 Engraving resistance vs.time at different angles of forcing cone

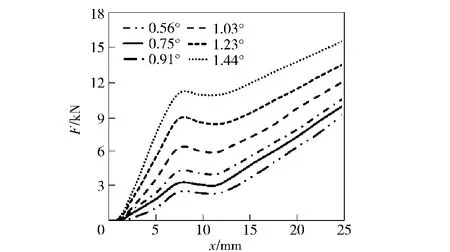
图6 不同坡膛角时挤进阻力随挤进位移变化图Fig.6 Engraving resistance vs.engraving displacement at different angles of forcing cone

基于随机响应面法构建的弹头挤进过程的代理模型与6组不同坡膛角对应的挤进阻力随位移的变化数据，采用MATLAB编写计算程序，获得挤进阻力以坡膛角和挤进位移为变量的计算公式如下:

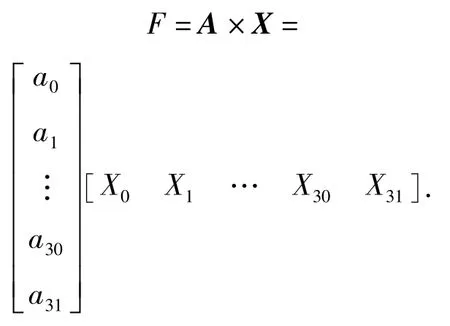
矩阵A为常数矩阵，采用逐步回归法通过MATLAB程序求解Hermite多项式中a0、ai1、ai1i2等待定系数获得。

矩阵X中:X0=1；X1=beta（1）；X2=m（1）；X3=beta（2）；X4=m（2）；X5=beta（1）×m（1）；X6= beta（3）；X7=m（3）；X8=beta（2）×m（1）；X9= beta（1）×m（2）；X10=beta（3）×m（1）；X11=beta（2）× m（2）；X12=beta（1）×m（3）；X13=m（4）；X14= beta（3）×m（2）；X15=beta（2）×m（3）；X16=beta（1）× m（4）；X17=m（5）；X18=beta（3）×m（3）；X19= beta（2）×m（4）；X20=beta（1）×m（5）；X21=m（6）；X22=beta（3）×m（4）；X23=beta（2）×m（5）；X24= beta（1）×m（6）；X25=m（7）；X26=beta（3）×m（5）；X27=beta（2）×m（6）；X28=beta（1）×m（7）；X29= beta（3）×m（6）；X30=beta（2）×m（7）；X31= beta（3）×m（7）.其中:m（0）=1；m（1）=2x；m（2）=4x2-2；m（3）=8x3-12x；m（4）=16x4-48x2+12；m（5）=32x5-160x3+120x；m（6）= 2x（32x5-160x3+120x）-10×（16x4-48x2+12）；m（7）=2x［2x（32x5-160x3+120x）-10×（16x4-48x2+12）］-12×（32x5-160x3+120x）；beta（1）=2β；beta（2）=4β2-2；beta（3）=8β3-12β.

5.3 计算与分析

根据建立的挤进阻力代理模型与考虑了挤进阻力的挤进过程动力学方程，计算了6种不同坡膛角下膛内火药燃气压力随挤进位移变化关系，如图7所示，结果显示，膛内火药燃气压力随着挤进位移增加而单调增加，挤进位移为25 mm时弹头完全嵌入膛线，此时的膛内火药燃气压力即挤进压力，随坡膛角的增加而变小。这是由于随着坡膛角度的增加，相同的弹头刻痕长度对应的挤进时间减小，火药燃烧时间减小导致压力变小。

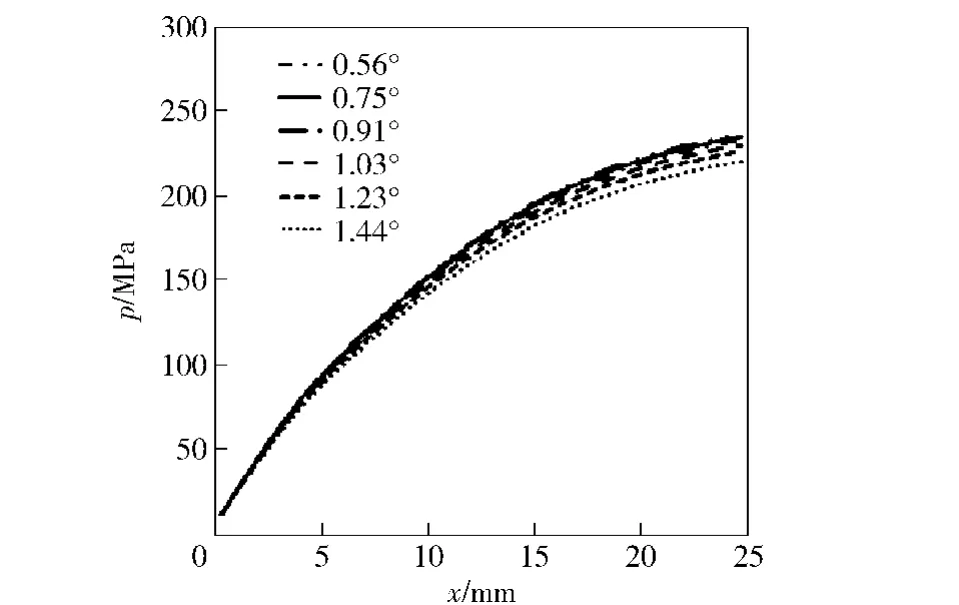
图7 膛内火药燃气压力随挤进位移的变化曲线Fig.7 Powder gas pressure vs.engraving displacement

基于挤进过程动力学方程，计算现有枪管长度下，弹头出膛口时的速度随坡膛角的变化曲线，如图8所示。弹头出膛口时的速度随着坡膛角的变化先增加后降低，这是由于坡膛角过小，会引起挤进时间过长，火药燃烧过于充分，坡膛角过大，会引起挤进时间过短，导致火药燃烧不充分，两种情况均会引起弹头在内弹道时期所受的弹后平均压力降低，导致弹头出膛口时的速度下降。由于某大口径枪弹技术指标要求初速大于810.0 m/s，在保证弹头初速的前提下，坡膛角的取值范围为0.11°～1.13°.

由于在阴线深度一定的条件下，坡膛角度越小，枪管坡膛五锥长度就越长，考虑到实际加工的可能性，坡膛五锥长度应在一定的合理范围内，即满足表1中所提出的枪管坡膛角的设计范围。因此坡膛角最优解的选择应满足3个方面的条件，即相对于原坡膛角度挤进压力减小、弹头初速最高、在枪管坡膛角的设计范围内。

本文所研究枪管的实际坡膛角度为0.85°，由图8可知，最高初速对应的坡膛角为0.53°，根据表1中有枪管坡膛角的设计范围，选取枪管的最佳坡膛角为0.56°；将实际坡膛角与本文所得最佳坡膛角0.56°分别采用有限元仿真方法分析和代入代理模型计算，获得仿真与代理模型分别计算所得挤进阻力随位移变化对比图如图9所示，显然两条仿真曲线均与代理模型计算得到的挤进阻力曲线具有较高的一致性，验证了代理模型的有效性，同时坡膛角为0.56°时，挤进阻力较小，坡膛受力较为缓和。

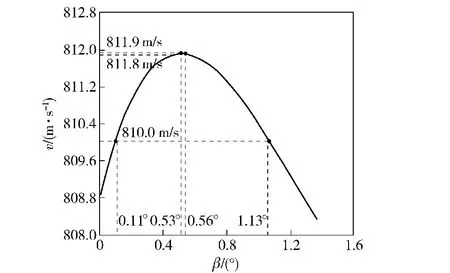
图8 弹头出膛口时的速度随坡膛角的变化曲线Fig.8 Muzzle velocity vs.forcing cone angle

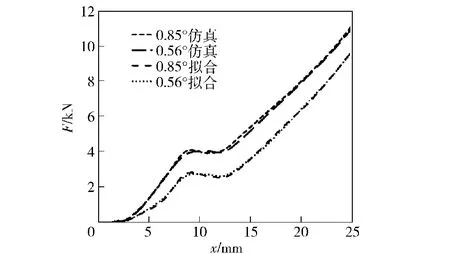
图9 挤进阻力随挤进位移变化对比图Fig.9 Engraving resistance vs.engraving displacement

6 结论

本文针对某大口径枪械内弹道挤进时期，进行了理论分析与数值仿真计算，得出以下结论:

1）对枪弹挤进过程的理论分析表明在枪管阳线宽度、缠角和导转侧角度等参数以及枪弹材料一定的情况下，挤进阻力仅与坡膛角和挤进位移有关。

2）通过建立不同坡膛角的有限元模型并进行仿真分析表明随着坡膛角度变大，挤进阻力达到的峰值越大，挤进阻力达到峰值的时刻越靠前，在达到峰值后挤进阻力有所下降并趋于稳定。

3）基于随机响应面法建立了挤进阻力与坡膛角及挤进位移的代理模型，数值解算得到了挤进阻力与坡膛角及挤进位移的函数表达式。

4）以经典内弹道方程组为基础，提出了考虑挤进阻力的枪弹挤进过程动力学方程。

5）弹头出膛口时的速度随着坡膛角的变化先增加后降低，对本文研究的某大口径机枪满足弹头初速条件的坡膛角度取值范围为0.11°～1.13°；在枪管坡膛角6种设计方案中满足弹头初速最高和挤进压力较小的最佳坡膛角为0.56°.

（

）

［1］ 欧学炳，殷仁龙，王学颜.自动武器结构设计［M］.北京:北京理工大学出版社，1995. OU Xue-bing，YIN Ren-long，WANG Xue-yan.Structure design of automatic weapons［M］.Beijing:Beijing Institute of Technology Press，1995.（in Chinese）

［2］ 丘尔巴诺夫E B.挤进时期内弹道学与挤进压力计算［M］.杨敬荣，译.北京:国防工业出版社，1997. Qierbarov E B.Interior ballistics and engraving force calculation during engraving of projectile［M］.YANG Jing-rong，translated. Beijing:National Defense Industry Press，1997.（in Chinese）

［3］ 段吉员，王彦平.弹丸挤进压力对平衡炮内弹道性能的影响研究［J］.高压物理学报，2006，20（2）:189-193. DUAN Ji-Yuan，WANG Yan-ping，et al.The effect of engraving force of projectile on interior ballistic performance of DAVIS Gun［J］.Chinese Journal of High Pressure Physics，2006，20（2）: 189-193.（in Chinese）

［4］ Joseph T S，Dipak K，Michael M.Small caliber modeling from design to manufacture to launch［C］∥23th International Symposium on Ballistics.Tarragona，Spain:International Ballistics Committee，2007:557-564.

［5］ 樊黎霞，何湘玥.弹丸挤进过程的有限元模拟与分析［J］.兵工学报，2011，32（8）:963-969. FAN Li-xia，HE Xiang-yue.Finite element simulation and process analysis of projectile entering into barrel［J］.Acta Armamentarii，2011，32（8）:963-969.（in Chinese）

［6］ 孙河洋，马吉胜，李伟，等.坡膛结构变化对火炮内弹道性能影响的研究［J］.兵工学报，2012，33（6）:669-675. SUN He-yang，MA Ji-sheng，LI Wei，et al.Study on influence of bore structure on gun's interior ballistic performances［J］.Acta Armamentarii，2012，33（6）:669-675.（in Chinese）

［7］ Johnson G，Cook W.Fracture characteristics of three metals subjected to various strains，strain rates，temperatures and pressures［J］.Engineering Fracture Mechanics，1985，21:31-48.

［8］ Basaga H B，Kaymaz I，Bayraktar A.An improved response surface method for reliability analysis of structures［J］.Structural Engineering and Mechanics，2012，42（4）:175-189.

［9］ Isukapalli S S，Ray A.Stochastic response surface methods（SRSMs）for uncertainty propagation:application to environmental and biological systems［J］.Risk Analysis，1998，18（3）:351-363.

Influence of Structure Parameters of Forcing Cone on Small Arms Interior Ballistics During Engraving

LU Ye1，ZHOU Ke-dong1，HE Lei1，LI Jun-song2，HUANG Xue-ying3
（1.School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China；2.No.208 Research Institute of China Ordnance Industries，Beijing 102202，China；3.Unit 63856 of PLA，Baicheng 137001，Jilin，China）

The working condition of barrel forcing cone is worse during the firing process of small arms. To study the influence of the forcing cone angles on the stress of barrel forcing cone，the three-dimensional finite element models of barrel and projectile at different forcing cone angles are established，in which the structures of barrel and projectile，and nonlinear constitutive relations are considered.The effects of different forcing cone angles on the projectile engraving process are analyzed.The data of engraving resistance is obtained under the condition of different forcing cone angles.A response surface model of engraving resistance is established.The formula and the variation rules of projectile engraving resistance along with the forcing cone angle and engraving displacement are calculated based on the above data by using Hermite polynomial.A dynamic model of projectile engraving process is established in consideration of the engraving resistance.The engraving pressure during the projectile engraving process is solved by programming.The forcing cone angles among 0.11°and 1.13°，which satisfy the requirement of muzzlevelocity of the projectile，are obtained，and then the best forcing cone angle of 0.56°，which could reduce the barrel stress to ensure the highest velocity and meet the design range of forcing cone angles in case of satisfying the interior ballistic behaviors，is got.

ordnance science and technology；barrel；projectile engraving；forcing cone；contact；impact

TJ303.9

A

1000-1093（2015）07-1363-07

10.3969/j.issn.1000-1093.2015.07.028

2014-09-18

陆野（1988—），男，博士研究生。E-mail:luye_njust@163.com；周克栋（1964—），男，教授，博士生导师。E-mail:zkd81151@njust.edu.cn