天波雷达欠密度流星余迹干扰抑制算法

薄超，顾红，苏卫民，陈金立

（1.南京理工大学电子工程技术研究中心，江苏南京210094；2.南京信息工程大学电子与信息工程学院，江苏南京210044）

天波雷达欠密度流星余迹干扰抑制算法

薄超1，顾红1，苏卫民1，陈金立2

（1.南京理工大学电子工程技术研究中心，江苏南京210094；2.南京信息工程大学电子与信息工程学院，江苏南京210044）

针对欠密度流星余迹干扰严重影响天波超视距雷达（OTHR）目标检测的问题，提出了欠密度流星余迹干扰抑制算法。应用二进小波变换（DWT）计算流星余迹干扰的位置，并将该位置的回波数据组成3阶Hankel张量；采用高阶正交迭代（HOOI）算法和总体最小二乘（TLS）算法，抑制张量中的噪声分量和求解流星余迹干扰参数，解得流星余迹干扰的时域回波数据；从回波数据中去除流星余迹干扰，得到干扰抑制后的时域回波数据。与现有流星余迹干扰抑制算法相比，该方法提高了目标的信杂噪比（SCNR）。

雷达工程；天波超视距雷达；流星余迹干扰；高阶正交迭代；二进小波变换

0 引言

天波超视距雷达（OTHR）工作在3～30 MHz的高频波段，其利用电离层对高频段信号的反射作用而实现超视距目标探测，在军事和民用领域得到应用［1-5］。然而OTHR工作的电磁环境较为恶劣，易受到短波通信、闪电和流星余迹等干扰的影响［6］，其中流星余迹干扰的危害较大，在频域中形成虚假目标和抬高噪声基底，因此提高OTHR的目标检测性能，抑制流星余迹干扰具有重要意义。

目前已提出多种抑制流星余迹干扰的方法［7-12］，其中特征值分解自回归（EVD-AR）算法［7］和奇异值分解自回归（SVD-AR）算法［8］均需要预先抑制海/地杂波，分形维自回归（FD-AR）算法［9］、小波变换自回归（WT-AR）算法［10］、小波变换（WT）算法［11］和复数据经验模型分解（CEMD）算法［12］均无需预先抑制海/地杂波。EVD-AR算法和SVD-AR算法完成抑制海/地杂波后，将突显出来的流星余迹干扰挖掘和重构，其中重构采用自回归（AR）模型恢复挖掉的数据；FD-AR算法和WT-AR算法分别采用分形维和WT检测数据的突变点以确定流星余迹干扰位置，流星余迹干扰位置确定后将被挖除并用AR模型重构，但AR模型具有模型阶数较难选择的缺陷。WT算法利用WT分解回波数据，将回波数据分解成近似分量和细节分量，根据细节分量检测流星余迹干扰位置，并采用对称插值方法抑制回波数据细节分量中的流星余迹干扰，此方法无需AR模型预测挖除数据，但回波数据近似分量中的流星余迹干扰无法抑制。采用CEMD算法分解时域数据，从而得到多个固有模态函数（IMF），根据第一个IMF的总体方差与局部方差的大小确定干扰的位置，计算时域数据与各IMF分量的相关系数，将最大相关系数之前的各IMF中干扰处数据置0后进行数据重构，此方法虽然无需AR模型预测数据，但各个IMF分量均含有目标回波，将流星余迹干扰处的IMF数据置0，会降低目标信杂噪比（SCNR）。除以上缺点外，上述算法亦不能准确计算流星余迹干扰终止时刻，抑制干扰后留有大量流星余迹干扰残余。

针对上述问题，引入二进小波变换（DWT）算法、高阶正交迭代（HOOI）算法和总体最小二乘（TLS）算法［13］，求得流星余迹干扰回波参数，准确计算流星余迹干扰终止时刻，减少干扰残余分量，提高OTHR检测性能。本文所提算法简称为DWTHOOI-TLS算法。

1 流星余迹干扰的特点和信号模型

根据报道，每天约有数百亿计的流星进入地球大气层，高速运动的流星与大气层发生摩擦燃烧形成电离气体柱，此电离气体柱就是流星余迹。流星余迹可反射高频电磁波而形成干扰，干扰回波进入OTHR后产生虚假目标和抬高噪声基底，降低OTHR的目标检测性能，此时的干扰信号就是流星余迹干扰。

流星余迹具有下列特征［14］：1）寿命与质量呈正比，持续时间在几毫秒至几秒之间，平均寿命约0.5 s；2）高度位于80～120 km之间；3）流星余迹干扰有时很强，从雷达波束旁瓣亦可进入。

依据流星余迹电子线密度（即流星余迹中单位长度内的电子数），流星余迹可分为欠密度余迹和过密度余迹两类［15］。二者均会对高频波段信号产生反射而形成干扰，影响OTHR的目标检测，但电子线密度每升高一个数量级，这个数量级流星余迹干扰的发生概率便为前一数量级的1/10［16］.因此过密度流星余迹出现的概率低于欠密度流星余迹出现的概率，以抑制欠密度流星余迹干扰（下文简称为流星余迹干扰）为主，选用数学模型［14］：

式中：smeteor（t）为流星余迹回波信号；h（t）为流星余迹后向散射信道响应；s（t）为雷达发射信号；A为信道响应初始幅值；α为信道响应衰减因子；τ为流星余迹干扰发生时间；fc为信道响应多普勒频率；β为信道响应初始相位。从流星余迹干扰信号模型可见，干扰开始时刻信号幅值较大，较易准确检测，当干扰幅值衰减到较低数值时，现有干扰抑制无法检测，导致干扰抑制后有较多残留分量剩余，因此采用DWT-HOOI-TLS算法计算干扰参数，准确求得其持续时间，减少干扰残余分量，提高OTHR检测性能。

2 流星余迹干扰抑制算法

算法思路：利用DWT估算流星余迹干扰存在的位置，将该位置的回波数据组成Hankel张量；采用HOOI算法和TLS算法，计算Hankel张量解得流星余迹干扰相关参数，组建流星余迹干扰时域回波信号，将流星余迹干扰时域回波从原始数据中消除；对流星余迹干扰抑制后的回波数据进行傅里叶变换求得其频谱，此时流星余迹干扰已消除，目标凸显。

2.1 估算流星余迹干扰位置

假设某一距离-方位分辨单元内存在干扰，在一个相干积累时间内采集数据为x（n）（1≤n≤N），则x（n）可表示为

式中：c（n）为海/地杂波；s（n）为目标回波；noise（n）为噪声。DWT是一种非抽取的WT，将一维信号分解为一个逼近信号和一个细节信号。其中，逼近信号主要体现一维信号的低频部分，细节信号主要体现一维信号的高频部分，且与原一维信号等长。流星余迹干扰能量较强且含有大量的高频分量，因此，采用一个滑窗在回波数据的DWT细节信号上滑动，通过比较滑窗内局部方差和总体方差来检测其产生和终止的位置，具体计算流程如下：

1）对x（n）进行DWT，求得其细节分量，其中变换公式为

式中：W2jf（n）为回波数据的细节信号；ψ（n）为与小波函数对应的尺度函数，且ψ2j（n）=1/2jψ（n/2j）.流星余迹干扰的能量主要集中在回波信号高频部分，即存在于W2jf（n）中，因此选取j=0时刻的W20f（n）判断流星余迹干扰存在位置。

2）设窗函数为

式中：L为窗函数长度。计算W20f（n）的标准方差，将作为检测瞬态干扰的门限值，ξ为尺度因子。让矩形窗在W20f（n）上滑动，计算窗内所含数据的标准方差.当出现第一个时，判断为干扰的起始位置，随后出现的第一个位置，判断为干扰的终止位置，将x（n）中对应的起始位置和终止位置间数据用x′（m）（1≤m≤M）表示，此段数据存在干扰。

2.2 求解流星余迹干扰回波信号参数

数据x′（m）中包含流星余迹干扰、海/地杂波、目标回波和噪声，而高频雷达中海杂波主要表现为两个单点频的Bragg峰［17］，因而x′（m）可表示为

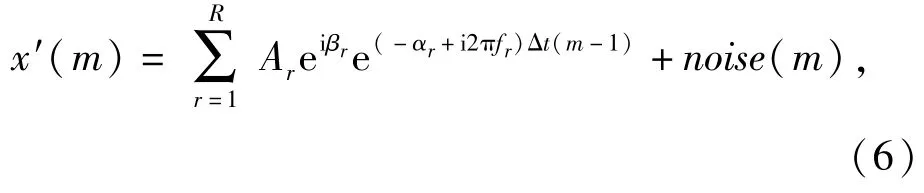
式中：R为单点频回波总数；Ar为第r个单点频回波的初始幅值；βr为第r个单点频回波的初始相位；αr为第r个单点频回波的衰减因子；fr为第r个单点频回波的多普勒频率；Δt为采样间隔。令，可得（6）式的紧凑形式为

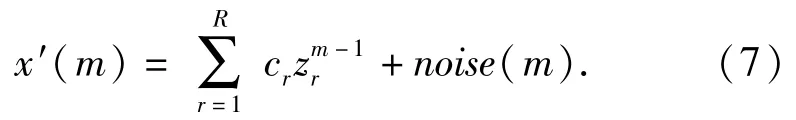
通常情况下，流星余迹干扰、海/地杂波和目标回波在信号强度和频率大小两方面具有显著的差异。在信号强度方面，海/地杂波和流星余迹干扰的强度大于目标；在频率大小方面，海/地杂波的频率低于流星余迹干扰，且可根据载频估算，而目标频率不固定。准确估计Ar、φr、αr和fr四个参数，根据Ar和fr的大小，即能分辨出流星余迹干扰对应的参数组，进而得到流星余迹干扰时域回波，因此采用HOOI-TLS算法计算上述4个参数。基于HOOI-TLS算法的流星余迹干扰参数计算流程如下：

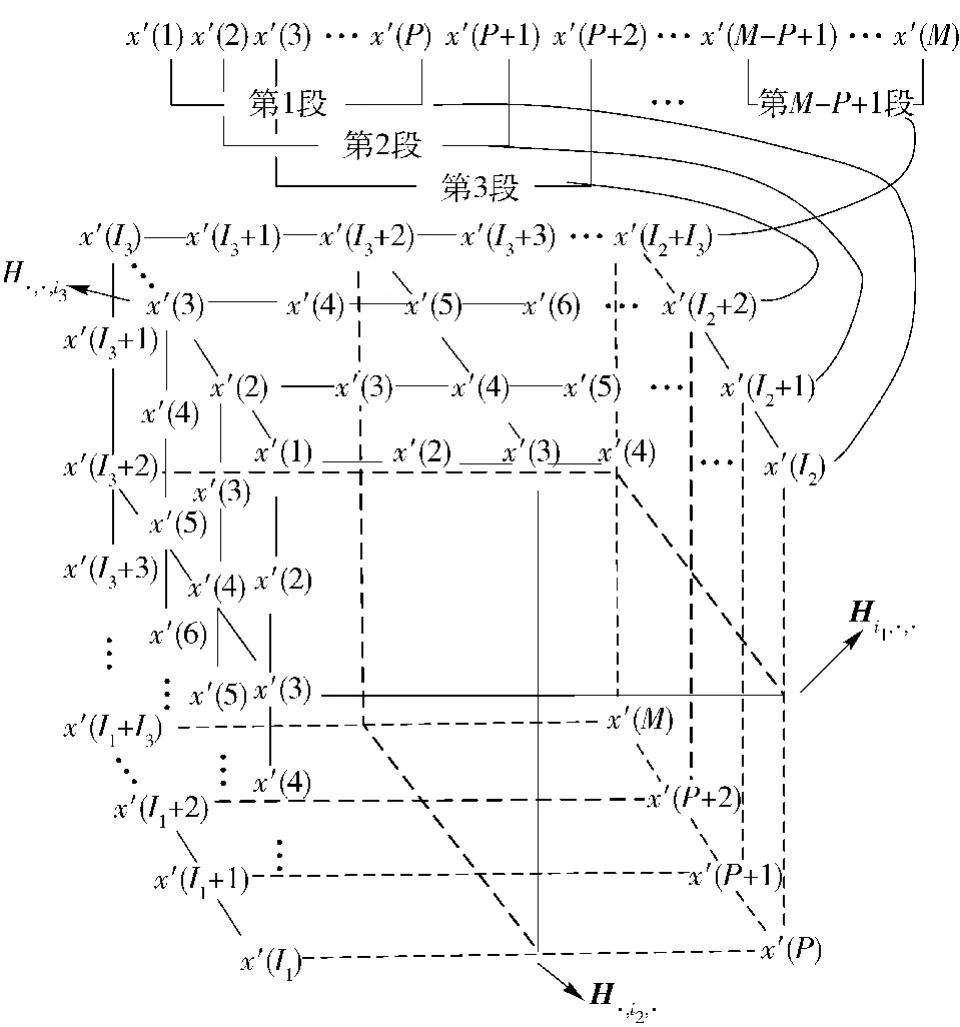
图1 流星干扰数据的Hankel张量表示Fig.1 Hankel tensor representation of meteor interference data

图1中，Hi1，·，·、H·，i2，·、H·，·，i3分别表示沿长、宽和高为i1、i2、i3切割的切片矩阵，且1≤ik≤Ik，k=1，2，3，I1+I2+I3=M+2，将各自的切片矩阵平铺，可得到张量的等效模式展开矩阵，其中等效模式展开矩阵与张量是一一对应关系。

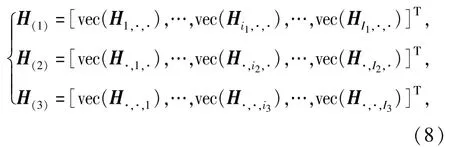
式中：H（k）（k=1，2，3）为第k等效模式展开矩阵；vec（·）表示矩阵按列展开。张量H中的元素与数据x′（m）之间的对应关系满足：

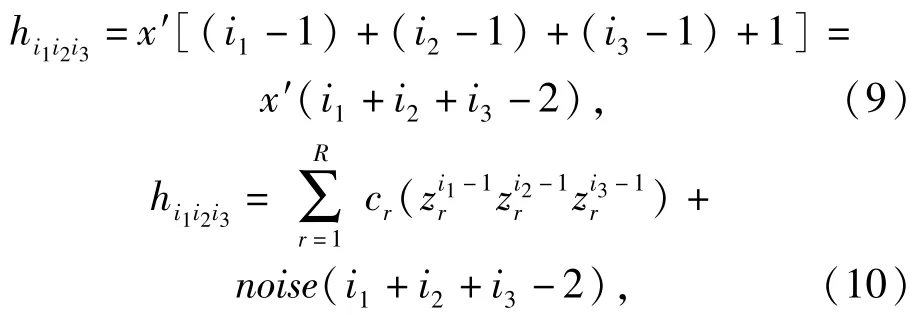
式中：hi1i2i3为张量H中长、宽、高分别为i1、i2、i3的元素。进而张量H分解为

式中：I′k=Ik-1（k=1，2，3）；N为3阶噪声张量。

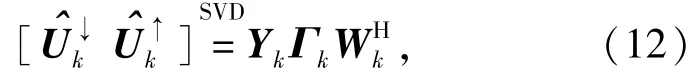
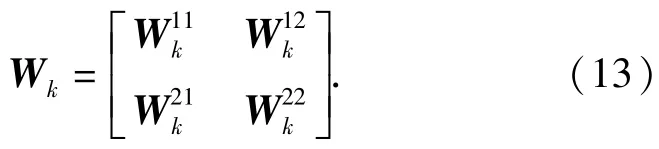
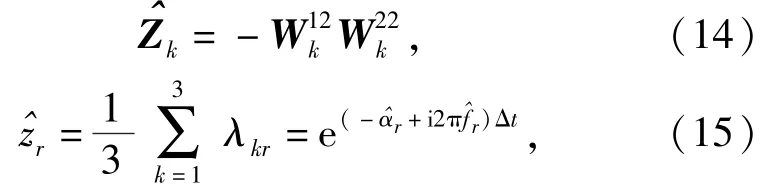
式中：λkr为的第r个特征值；为zr的估计值。计算的幅值和相位即可得.

5）根据（7）式可得方程

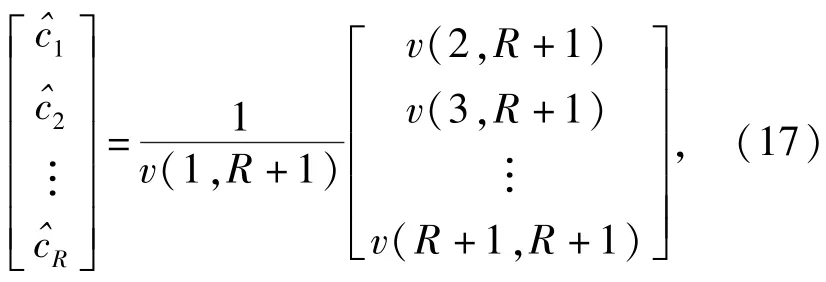
2.3 计算流星余迹干扰持续时间和消除流星余迹干扰

当流星余迹干扰幅值低于OTHR的噪声基底时，可认为其影响可忽略，由（无回波信号时OTHR的噪声基底）3个参数可确定流星余迹干扰的截止时刻，由此可得流星余迹干扰的时域回波数据.

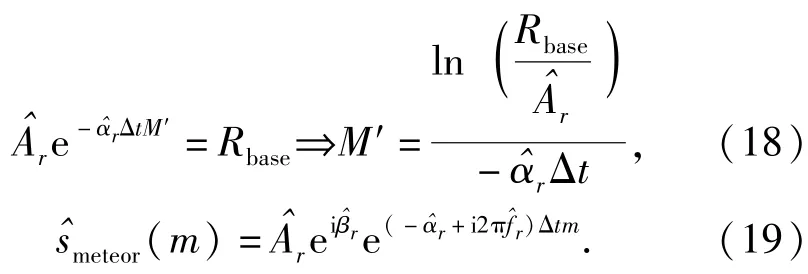
将干扰从回波数据中减去得

式中：y为流星余迹干扰抑制后的数据矢量；x为流星余迹干扰抑制前的数据矢量；为求得流星余迹干扰的数据矢量。对数据矢量y进行傅里叶变换，可得干扰抑制后的频谱，此时被干扰掩盖的目标突显出来。

2.4 算法步骤

步骤1 通过DWT计算流星余迹干扰中较强回波存在的位置，截取该数据段x′（m），而后根据（9）式将数据x′（m）表示成3阶Hankel张量。

步骤2 采用HOOI算法求解张量H的近似张量H′，进而求得H′等效模式展开矩阵H′（k）的左奇异矩阵前R列.

步骤4 根据（20）式将流星余迹干扰从时域上消除得y，对数据矢量y进行傅里叶变换得到干扰抑制后的频谱。

2.5 算法时间复杂度分析

DWT-HOOI-TLS算法主要分为干扰位置检测和参数计算两部分。其中：干扰位置检测需进行2N2+（2L+1）N+L+1次基本运算，从而干扰位置检测的时间复杂度为T1（n）=o（n2）；而干扰参数计算中，HOOI算法的时间复杂度最高，且SVD算法的时间复杂度为o（mn·min（m，n）），因此干扰参数计算的时间复杂度为T2（n，m）=o（mn·min（m，n））.由上述分析可得DWT-HOOI-TLS算法的时间复杂度为T（n）=T1（n）+T2（n，m）=o（mn·min（m，n））.

3 仿真实验

仿真实验采用高频雷达实测海/地杂波数据，对比CEMD算法［12］、WT-AR算法［10］、WT算法［11］和DWT-HOOI-TLS算法的流星余迹干扰抑制性能。为了说明DWT-HOOI-TLS算法的有效性，实验部分采用了6个不同距离单元的实测数据对其验证。在高频雷达实测数据中加入流星余迹干扰，干扰与杂波加噪声之比为-2 dB；干扰信道响应衰减因子α= 8；干扰发生时间τ=1.2 s；干扰信道响应多普勒频率fc=-20 Hz；干扰信道响应初始相位β=2.9 rad/s；干扰持续时间为0.96 s.HOOI算法门限值ε= 10-6；DWT算法选用haar小波；单点频总数R=4；尺度因子ξ=1.

3.1 仿真实验1

实测数据中加入目标的多普勒频率为-17 Hz，目标SCNR为-25 dB.实测数据中加入流星余迹干扰和目标后的时域波形和频域波形分别如图2（a）和图2（b）所示，其中干扰信道响应初始幅值A= 172.4 dB·mV，雷达噪声基底电平Rbase=28 dB·mV.图2（a）为在1.2 s时刻出现了较强的干扰，持续一段时间后消退；图2（b）为在-20 Hz处存在一个幅值较高和频带较宽的干扰，将噪声基底抬高，掩盖了-17 Hz处的目标。

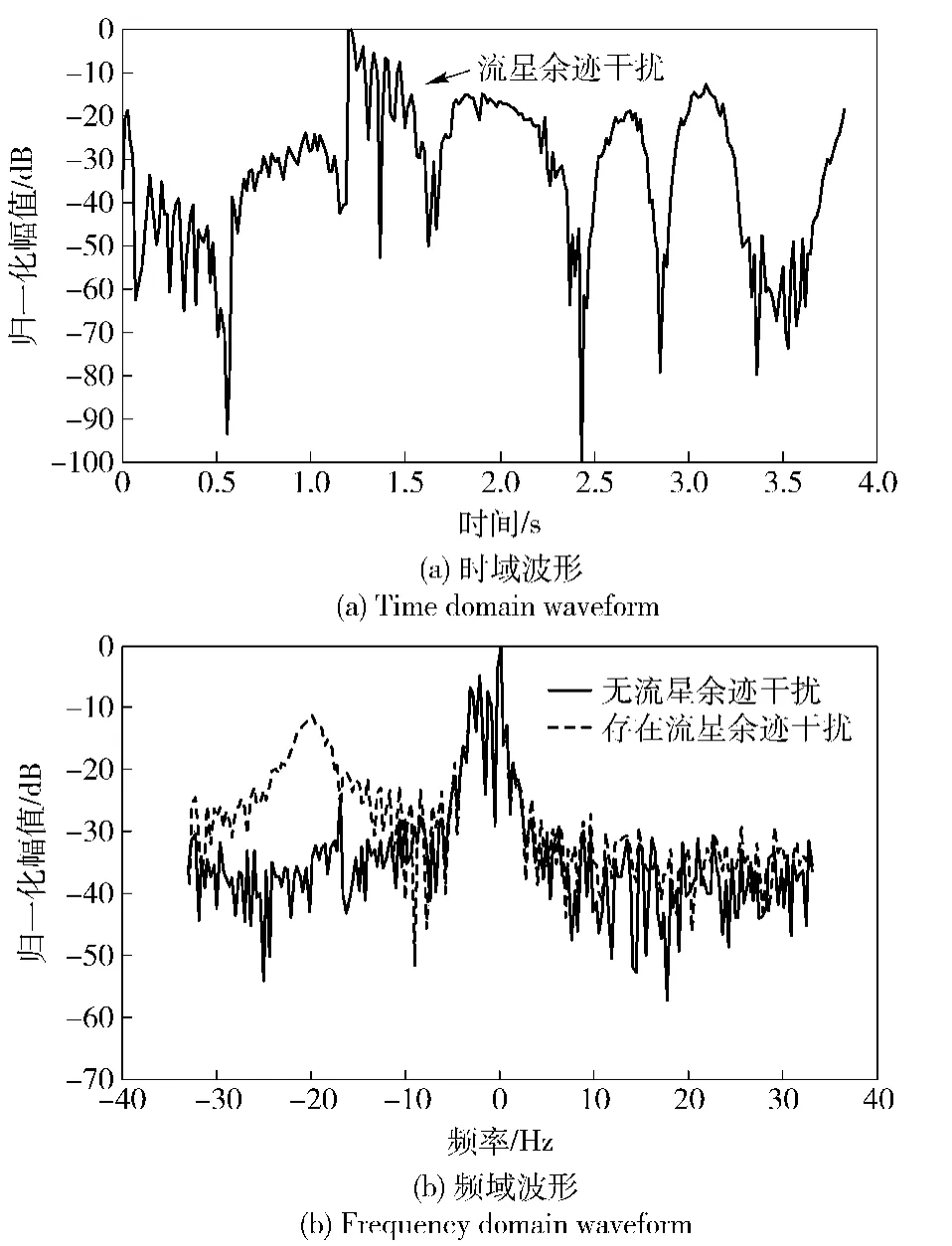
图2 加入流星余迹干扰和目标的实测数据Fig.2 Measured data with added meteor trail interference and objectives

应用DWT算法估算干扰位置，其中总体方差与滑窗内的局部方差比较结果如图3所示，可估干扰开始和终止时刻分别为1.2s和1.6s，说明此方法能够准确估计干扰的起始位置和粗略估计干扰的终止时刻。

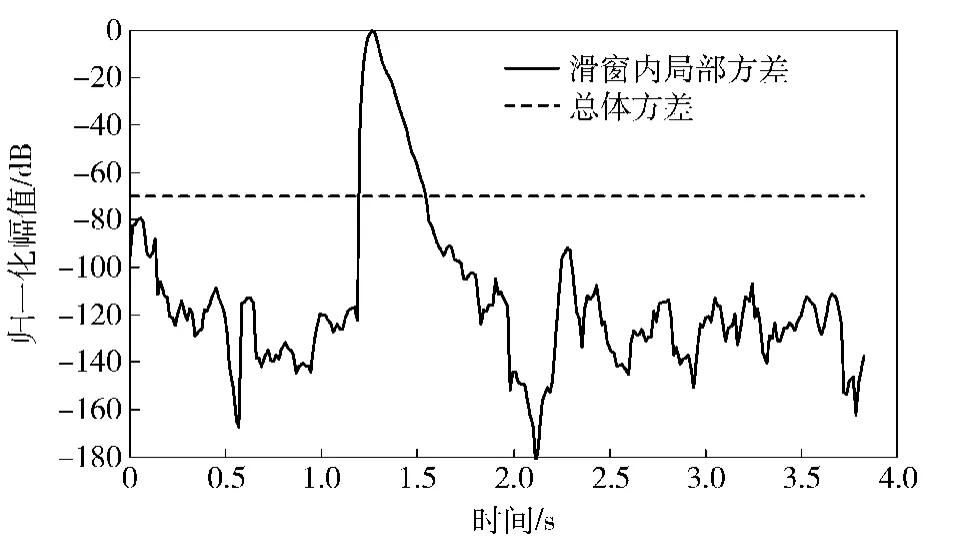
图3 滑窗内局部方差与总体方差对比图Fig.3 The comparison between local variance within the sliding window and overall variance

分别应用DWT-HOOI-TLS算法、CEMD算法、WT-AR算法和WT算法抑制流星余迹干扰后的频谱如图4所示。

图4显示了4种算法均能抑制流星余迹干扰和突显目标，但与DWT-HOOI-TLS算法相比，CEMD算法、WT-AR算法和WT算法干扰抑制后噪声基底较高，干扰残余较多而形成虚假目标，提高了雷达目标检测的虚警率。上述现象是由于3种算法均未能检测和抑制干扰中能量较弱的部分，导致干扰抑制后留有大量干扰残余，而DWT-HOOI-TLS算法利用回波参数计算干扰持续时间，更加准确地计算干扰截止时刻，有效地减少了干扰抑制后的残留分量。将图4（a）中目标所在位置放大后，如图4（b）所示，与DWT-HOOI-TLS算法相比，CEMD算法的目标SCNR较低。这是由于CEMD算法抑制干扰所在位置的高频分量，而目标径向速度较快时也表现为高频，从而抑制干扰的同时，亦抑制目标信号而引起目标SCNR降低。DWT-HOOI-TLS算法能够准确计算干扰存在的位置，并将干扰从时域消除，未影响目标回波信号，不会引起目标SCNR损失，因此不存在上述问题。

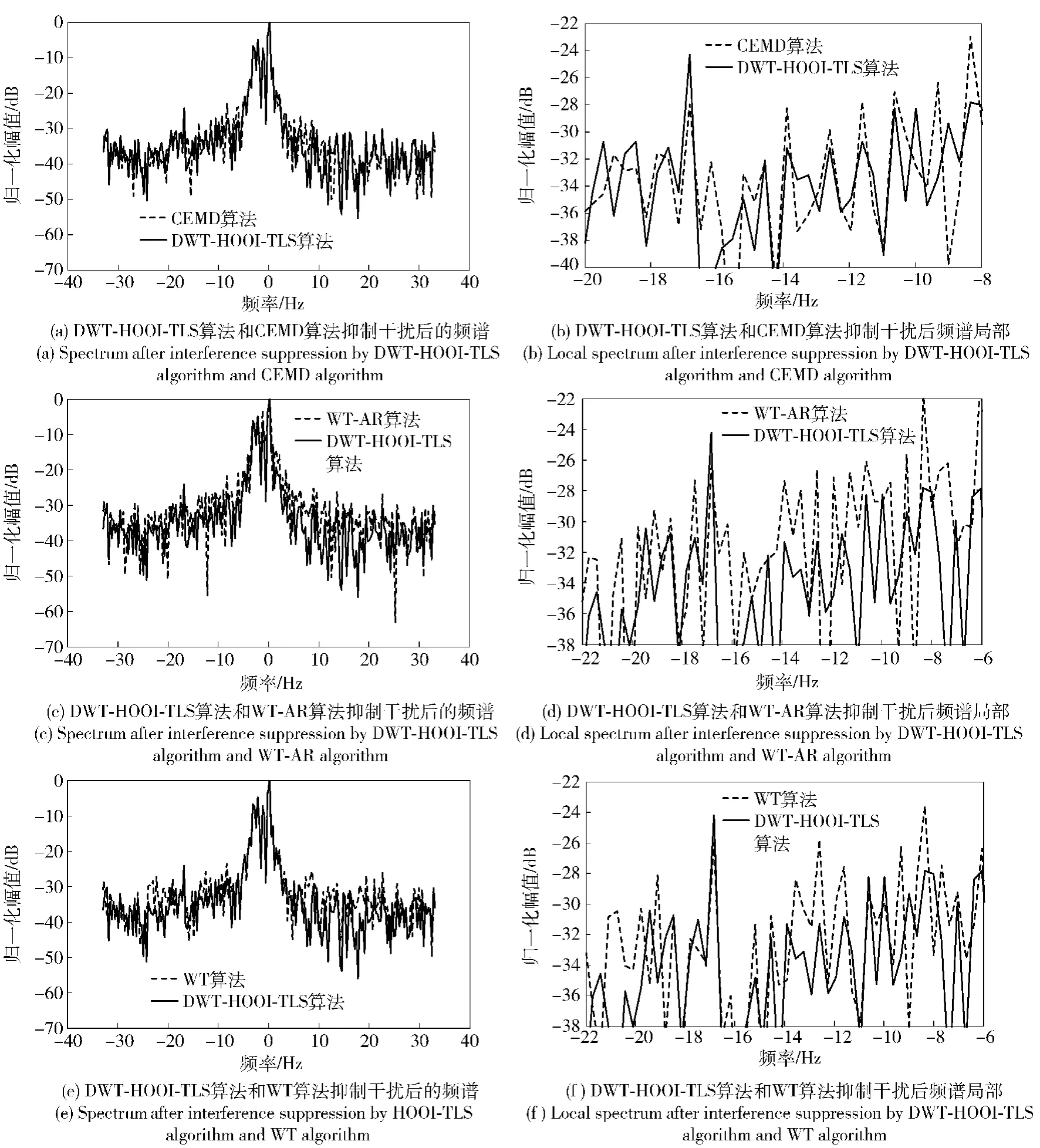
图4 DWT-HOOI-TLS算法、CEMD算法、WT-AR算法和WT算法抑制流星余迹后频谱Fig.4 Spectral after interference suppression by DWT-HOOI-TLS algorithm，CEMD algorithm，WT-AR algorithm and WT algorithm

采用HOOI算法和TLS算法计算干扰的相关参数，6组计算结果和误差的均值如表1所示，DWTHOOI-TLS算法计算值与真实值之间误差较小，能准确地重构干扰回波信号。

表1 干扰参数的计算值与真实值对比结果Tab.1 Comparative results of calculated value and true value of interference parameters

分别计算6组实验的干扰参数、干扰截止时刻和算法运算时间，并分别与CEMD算法、WT-AR算法和WT算法进行比较。比较结果为4种算法的运算时间相近，而DWT-HOOI-TLS算法计算的干扰持续时间更加逼近真实值。产生此结果的原因是干扰产生时刻信号较强，现有算法均能有效检测，但随着干扰信号强度的逐渐减弱，现有算法的检测性能会下降，而DWT-HOOI-TLS算法利用干扰的时域参数计算其持续时间，避开直接检测干扰较弱部分，进而更加精确的计算截止时刻。

3.2 仿真实验2

分别在6个实测数据中加入单个目标和干扰，计算干扰抑制前后的SCNR，并求其均值绘制SCNR变化曲线，其中目标多普勒频率为-17 Hz，目标SCNR变化范围为-30～-25 dB.图5分别为采用DWT-HOOI-TLS算法、CEMD算法、WT-AR算法和WT算法抑制干扰后的SCNR均值变化曲线。

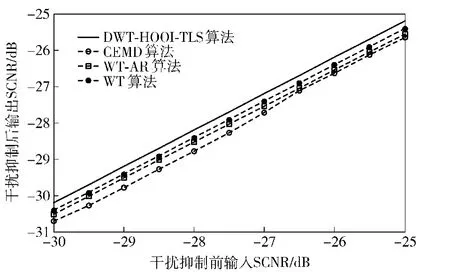
图5 DWT-HOOI-TLS算法、CEMD算法、WT-AR算法和WT算法抑制干扰后的SCNR变化曲线Fig.5 SCNR curves after interference suppression by DWTHOOI-TLS algorithm，CEMD algorithm，WT-AR algorithm and WT algorithm

由图5可见，DWT-HOOI-TLS算法的输出SCNR最高，WT-AR算法和WT算法的输出SCNR次之，而CEMD算法的输出SCNR最低。上述现象是由于DWT-HOOI-TLS算法能够准确计算干扰持续时间，在时域上将干扰信号消除，降低干扰残留，减少对目标回波的影响，从而获得较高的输出SCNR，而WT-AR算法和WT算法未能准确估计干扰的持续时间，干扰抑制后留有大量干扰残余，导致输出SCNR偏低，CEMD算法不能准确估计干扰持续时间，且在其消除干扰的同时抑制高速目标信号，引起输出SCNR损失最大。

4 结论

本文利用DWT-HOOI-TLS算法解得流星余迹干扰时域回波参数，在时域上消除干扰，降低干扰残余和突显目标，且在消除干扰的同时不抑制目标信号。仿真实验表明，与现有算法相比，本文算法能够更加准确地估计干扰的持续时间，有效地减少流星余迹残余分量，且提高了目标SCNR.

（

）

［1］游伟，何子述，陈绪元，等.基于三次相位建模的天波雷达污染校正［J］.电波科学学报，2012，27（5）：875-880. YOU Wei，HE Zi-shu，CHEN Xu-yuan，et al.Skywave radar decontamination based on the cubic phase model［J］.Chinese Journal of Radar Science，2012，27（5）：875-880.（in Chinese）

［2］Quan Y，Xing M，Zhang L，et al.Transient interference excision and spectrum reconstruction for OTHR［J］.Electronics Letters，2012，48（1）：42-44.

［3］李宗强，顾红，苏卫民，等.天波超视距雷达中短波干扰的抑制［J］.兵工学报，2003，24（3）：330-333. LI Zong-qiang，GU Hong，SU Wei-min，et al.Suppression of shortwave jamming for the over the horizon radar［J］.Acta Armamentarii，2003，24（3）：330-333.（in Chinese）

［4］吴瑕，陈建文，鲍拯，等.新体制天波超视距雷达的发展与研究［J］.宇航学报，2013，34（5）：671-678. WU Xia，CHEN Jian-wen，BAO Zheng，et al.Development and research on new system skywave over-the-horizon radar［J］.Journal of Astronautics，2013，34（5）：671-678.（in Chinese）

［5］罗欢，陈建文，鲍拯.一种天波超视距雷达电离层相位污染联合校正方法［J］.电子与信息学报，2013，35（12）：2829-2835. LUO Huan，CHEN Jian-wen，BAO Zheng.A joint method to correct ionospheric phase perturbation in over-the-horizon radar［J］. Journal of Electronics&Information Technology，2013，35（12）：2829-2835.（in Chinese）

［6］周文瑜，焦培楠.超视距雷达技术［M］.北京：电子工业出版社，2008：187. ZHOU Wen-yu，JiAO Pei-nan.Over the horizon radar technology［M］.Beijing：Publishing House of Electronic Industry，2008：187.（in Chinese）

［7］邢孟道，保铮，强勇.天波超视距雷达瞬态干扰抑制［J］.电子学报，2002，30（6）：823-826. XING Meng-dao，BAO Zheng，QIANG Yong.Transient interference excision in OTHR［J］.Acta Electronica Sinica，2002，30（6）：823-826.（in Chinese）

［8］陈希信，黄银河.基于矩阵奇异值分解的高频雷达瞬态干扰抑制［J］.电子与信息学报，2005，27（12）：1879-1882. CHEN Xi-xin，HUANG Yin-he.A SVD-based approach of suppressing transient interference in high-frequency radar［J］.Journal of Electronics&Information Technology，2005，27（12）：1879-1882.（in Chinese）

［9］Liu T，Gong Y H，Wei M，et al.Fractal features and detection of meteor interference in OTHR［C］//2006 CIE International Conference on Radar.Shanghai：IEEE，2006：1-5.

［10］权太范，李健巍.高频雷达抗瞬时干扰研究［J］.现代雷达，1999，21（2）：1-6. QUAN Tai-fan，LI Jian-wei.A study on high frequency radar suppressing sudden interference［J］.Modern Radar，1999，21（2）：1-6.（in Chinese）

［11］强勇，侯彪，焦李成，等.天波超视距雷达抑制流星余迹干扰方法的研究［J］.电波科学学报，2003，18（1）：23-27. QIANG Yong，HOU Biao，JIAO Li-cheng，et al.An approach of suppressing meteor trail interference in over-the-horizon radar［J］.Chinese Journal of Radio Science，2003，18（1）：23-27.（in Chinese）

［12］周忠根，水鹏朗.基于复数据经验模式分解的天波超视距雷达瞬态干扰抑制［J］.电子与信息学报.2011，33（12）：2831-2836. ZHOU Zhong-gen，SHUI Peng-lang.Transient interference suppression based on complex empirical mode decomposition in Overthe-Horizon radar［J］.Journal of Electronics&Information Technology，2011，33（12）：2831-2836.（in Chinese）

［13］Papy L M，De Lathauwer L，Van Huffel S.Exponential data fitting using multilinear algebra：the single-channel and multi-channel case［J］.Numerical Linear Algebra with Applications，2005，12（8）：809-826.

［14］刘涛.超视距雷达抗瞬态干扰算法研究［D］.成都：电子科技大学，2009. LIU Tao.Research on transient interference algorithm for OTHR［D］.Chengdu：University of Electronic Science and Technology of China，2009.（in Chinese）

［15］陈新莲.流星余迹散射特性及对电子系统性能的影响［D］.西安：西安电子科技大学，2002. CHEN Xin-lian.Meteor trails scattering properties and its effects on electronic systems performance［D］.Xi′an：Xidian University，2002.（in Chinese）

［16］魏旻，李军，龚耀寰.天波超视距雷达中流星余迹干扰模型［J］.电波科学学报，2007，22（3）：390-394. WEI Min，LI Jun，GONG Yao-huan.Meteor trail interference model in over-the-horizon radar［J］.Chinese Journal of Radio Science，2007，22（3）：390-394.（in Chinese）

［17］赵志国，陈建文，鲍拯.一种改进的OTHR自适应海杂波抑制算法［J］.系统工程与电子技术，2012，34（5）：909-914. ZHAO Zhi-guo，CHEN Jian-wen，BAO Zheng.Modified adaptive ocean clutter suppression approach in OTHR［J］.Systems Engineering and Electronics，2012，34（5）：909-914.（in Chinese）

［18］Lieven D L，Bart D M，Joos V.A multilinear singular value decomposition［J］.SIAM Journal on Matrix Analysis and Applications，2000，21（4）：1253-1278.

Under-dense Meteor Trail Interference Suppression Algorithm for Over-the-horizon Radar

BO Chao1，GU Hong1，SU Wei-min1，CHEN Jin-li2
（1.Research Centre of Electronic Engineering Technology，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China；2.School of Electronic and Information Engineering，Nanjing University of Information Science and Technology，Nanjing 210044，Jiangsu，China）

An under-dense meteor trail interference suppression algorithm is proposed to solve the problem of that under-dense meteor trail interference severely affects the target detection performance of overthe-horizon radar（OTHR）.The dyadic wavelet transform（DWT）algorithm is utilized to calculate the position of meteor trail interference，and Hankel tensor of three orders is constructed by the data of meteor trail interference.Then the noise component of tensor is refrained and the parameter of meteor trail interference is resolved by higher order orthogonal iteration（HOOI）algorithm and total least squares（TLS）algorithm，thus attaining the echo data of meteor trail interference in time domain.The meteor trail interference is subtracted from echo data to obtain the echo data after the meteor trail interference is refrained. Compared with existing meteor trail interference suppression methods，the proposed method could improve signal-to-clutter and noise ratio（SCNR）of target.

radar engineering；over-the-horizon radar；meteor trail interference；higher order orthogonal iteration；dyadic wavelet transform

TN958.93

A

1000-1093（2015）05-0846-08

10.3969/j.issn.1000-1093.2015.05.012

2014-07-08

国家自然科学基金项目（61302188）；国家部委预先研究基金项目（9140A07010713BQ02025、CASC04-02）；江苏省自然科学基金项目（BK20131005）；高等院校博士学科点基金项目（20113219110018）

薄超（1983—），男，博士研究生。E-mail：bochao417@163.com；顾红（1967—），男，教授，博士生导师。E-mail：guhongrceet@gmail.com