基于捷联导引头测角信息的弹目相对位置估计方法
2015-11-15任高峰张拥军张金鹏
任高峰,张拥军,张金鹏,2
(1. 中国空空导弹研究院,河南 洛阳 471009;2. 航空制导武器航空科技重点实验室,河南 洛阳 471009)
0 引 言
与传统框架式导引头相比,捷联导引头具备结构简单、重量轻、体积小、成本低、可靠性高等优点,目前已经成为制导系统中一个重要发展方向[1-3]。然而,由于捷联导引头固联安装于弹体上,测得的角度信息与弹体姿态完全耦合,不能直接得到可用于制导的有用信息;同时,由于弹体姿态信息及导引头测量信息中均含有测量噪声,给目标信息提取增加了困难。因此,如何在含有噪声并且与弹体姿态耦合的测量信息中提取可用的制导信息,成为制约捷联导引头使用的一项关键技术。
目前,由于比例导引律的广泛应用,针对捷联导引头测量信息的视线角速度提取成为研究热点。文献[4]针对导弹运动过程中系统噪声不断变化这一问题,结合样条滤波和IMM 算法设计IMM-SF 滤波器进行视线角速率估计,取得良好效果;文献[5]系统地对多种具有代表性的解耦方案和视线角速率重构方案进行分析,包括附加速率补偿法、抖动自适应法、相控阵雷达前馈补偿法和卡尔曼滤波法,对各方案进行对比研究,总结了其在工程应用中存在的问题;文献[6]在对全捷联导引头数学模型线性化展开的基础上,提出微分结合稳态Kalman 滤波方法估计体视线角速度的方法;文献[7]对全捷联导引头的去耦算法进行了研究;文献[8-9]则针对寄生回路对制导系统的影响进行了分析。
然而,在导弹飞行过程中由于弹体姿态的运动可能使得目标在导引头视场之外,仅提取视线角速度信息对处理这种情况难度很大,同时也限制了其他导引律的使用。因此,本文以导弹攻击静止目标为例,从分析系统的可观性出发,利用奇异值分解的方法,提出一种基于捷联导引头测角信息的弹目相对位置估计方法。
1 算法的基本原理
如果导弹在多个时刻测得弹目视线方向,若导引头测量和导弹测量时刻的姿态没有误差,则每次测得的视线方向均经过目标点,根据任意两次的测量结果,结合导弹自身所携带惯导系统给出的导弹位置、姿态信息,就可以利用三角形关系求出目标点相对于导弹的矢量,进而得到目标在导航坐标系下的坐标,其原理示意图见图1。
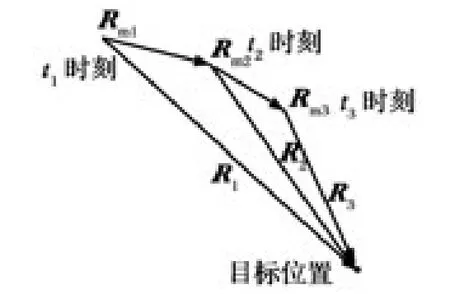
图1 算法的基本原理示意图
导引头的测量误差、导弹测量时的姿态误差都会使测得的弹目相对位置矢量和真实的弹目相对矢量方向存在一定偏差,造成多次测量得到的弹目相对矢量方向并不交于一点。为了使求取的坐标点与真实坐标点之间的偏差最小,采取求取一点坐标,使其到各次测量得到射线的距离平方和达到最小,其原理示意图见图2。
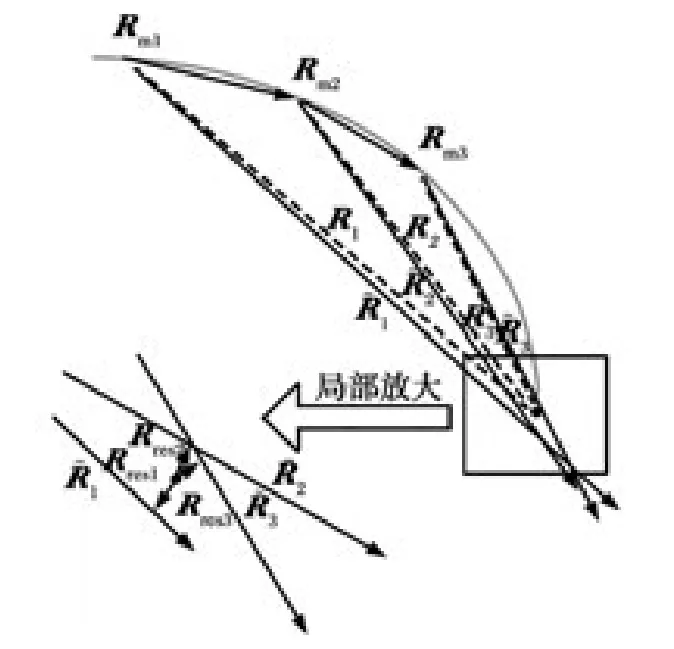
图2 测量存在噪声情况下的原理示意图
假设第i 次测得的导弹-目标方向矢量~Ri=[limini]T,此时对应的导弹位置矢量Xmi= [xiyizi]T,目标位置矢量Xt= [x y z]T,则目标位置距离第i 次测量矢量之间的距离di可以表示为
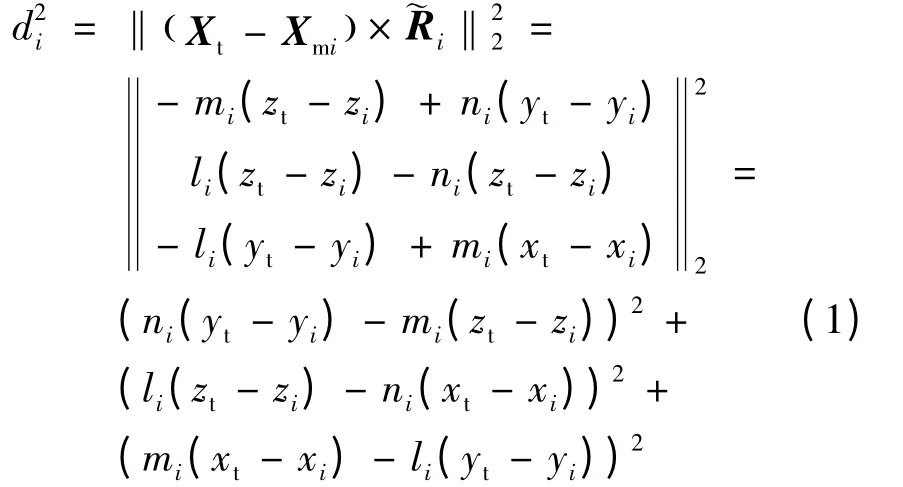
假定取n个时刻的测量值对目标位置进行计算,取指标函数:

将式(2)对Xt求导得到
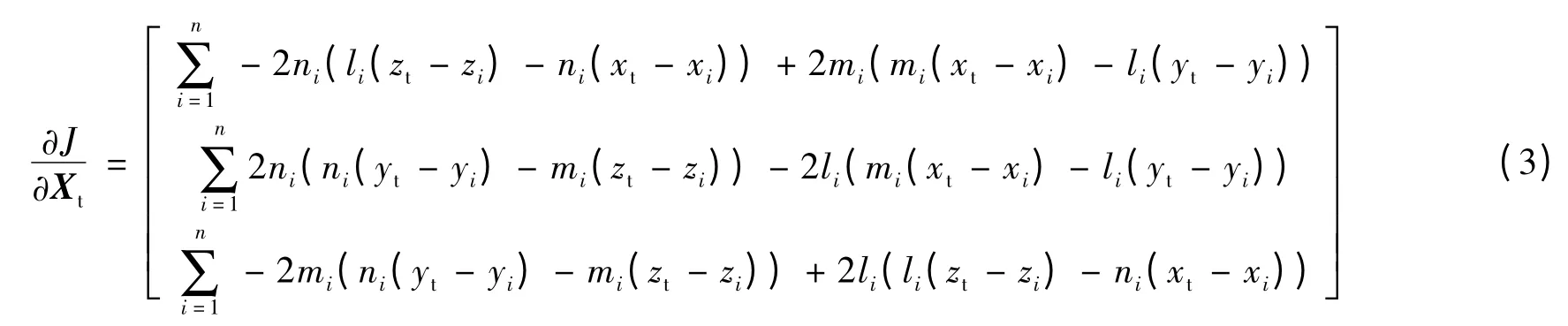
经整理得到
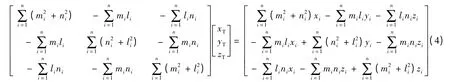
式(4)的解即为目标位置的最小二乘估计,为了后续描述简便,将式(4)重新写为

根据式(5)可知,当矩阵A可逆时,可以求得目标的位置。通过图1 ~2 可以看出,当弹目相对运动方向与弹目连线方向相同时,构不成三角形关系,矩阵A 不可逆,得不到目标位置;当弹目相对运动方向与弹目连线方向成一定夹角时,构成三角形关系,矩阵A 可逆,可以求得目标点的坐标值。
2 系统可观性分析
通过以上分析可知,当弹目相对运动方向与弹目连线成一定夹角时,矩阵A 可逆,系统可观。然而,在实际系统中测量误差和系统误差不可避免,还需要考虑方程(5)在观测量存在误差时的求解稳定性问题。为了详细分析,对矩阵A 进行奇异值分解,则式(5)可以变换为

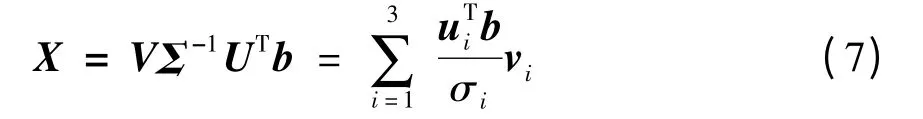
对应的均方差为
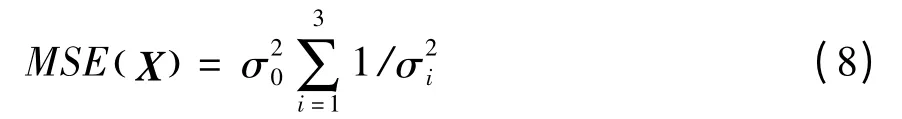
可以看出,矩阵A的奇异值直接影响最小二乘解的方差,当矩阵A 呈病态时,A 会有一个或者多个接近于0 的奇异值σi,从式(8)可知,当σi很小时,最小二乘解的均方误差将会很大,说明当存在测量噪声时,系统求解得到的弹目相对位置有很大起伏,影响其在制导回路中的使用。
对于本问题,不论是δb 还是δA,均来自导弹本身的定位误差、导弹姿态误差、以及导引头的测量误差等因素,在具体的分析过程中,这种误差对求解精度的影响用“条件数”这一概念进行评估。矩阵A 的条件数定义为A 的最大奇异值和最小奇异值之比,条件数越大,这种误差对方程(5)的影响越大,求解稳定性越不好。当条件数趋近于1时,系统对测量误差及导弹姿态误差的抗干扰能力达到最强,图3 ~4 是某典型条件下求得的条件数和奇异值。
从图3 可以看出,某典型条件下系统中矩阵A的条件数持续在50 以上,并且最高时达到将近500,可以看出,对于此典型条件来说,系统求解得到的相对位置受测量噪声和系统噪声的影响较大,即系统可观性不好。通过图4 可以看出,系统有一个奇异值在零附近,其对应项的误差将会因此而放大。
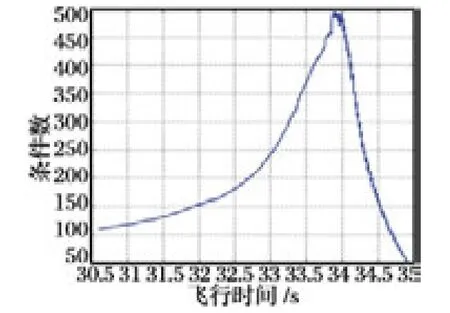
图3 某典型条件下矩阵的条件数
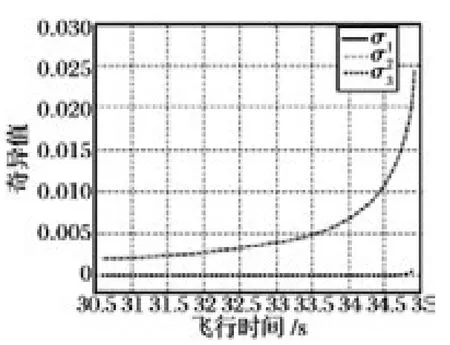
图4 某典型条件下矩阵的奇异值
在导弹攻击目标时,由于导弹朝向目标飞行,通常弹目视线方向和弹目相对速度方向夹角较小,这种情况下系统的可观性比较弱,描述系统方程(5)属于一个病态方程,对其进行求解需要特殊处理,以减少弱可观条件下测量噪声对算法结果的影响。
3 弱可观条件下算法的适应性改进
基于多次测量的弹目相对位置估计问题可以归纳为一个病态方程求稳定解的问题。根据相关文献报道,针对病态矩阵求稳定解的方法主要有截断奇异值分解法和修正奇异值分解法[10]。本文采用截断奇异值分解法对此问题进行求解,基本思路为:由于病态问题中最小二乘解不稳定的主要原因是系统方程矩阵存在接近于0 的奇异值,而使均方误差趋向无穷大。一个直观的想法就是去掉那些接近于零的奇异值,以损失估计的无偏性来换取均方误差的减小。对于导弹攻击静止目标的弹目相对位置估计问题来说,只有一个奇异值接近0,而另外两个处于相当水平。因此,求解步骤可以写为
(1)选取n个时刻的测量值(测角信息)及导弹在惯性系下的位置和姿态信息;
(2)根据式(4)写出方程AX = b 中矩阵A 和向量b 的具体形式;
(3)对矩阵A 进行奇异值分解,得出矩阵A 的奇异值σi及与奇异值对应的奇异值向量ui和vi,并对奇异值进行排序,假定σ1>σ2>σ3;
(4)判断是否满足条件σ1/σ3>R,其中R 为选定的阈值(在程序中选为5),若满足,取n = 2,若不满足,取n = 3,然后按照式(9)进行计算:
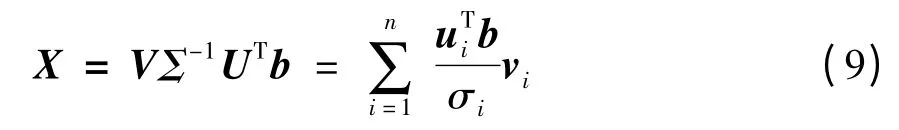
4 仿真验证与分析
将设计算法在仿真环境中实现,对算法进行仿真验证,导弹在飞行24.2 s 处截获目标,为了考虑测得的相对位置方向矢量误差对结果的影响,给出了造成该误差的主要因素:导弹姿态误差和导引头测量误差。图5 给出了不同时刻对应的导弹姿态误差,导引头测量误差为零均值的高斯白噪声,对应的标准差为0.007 5 rad,图6 ~9 给出了相应的仿真结果。
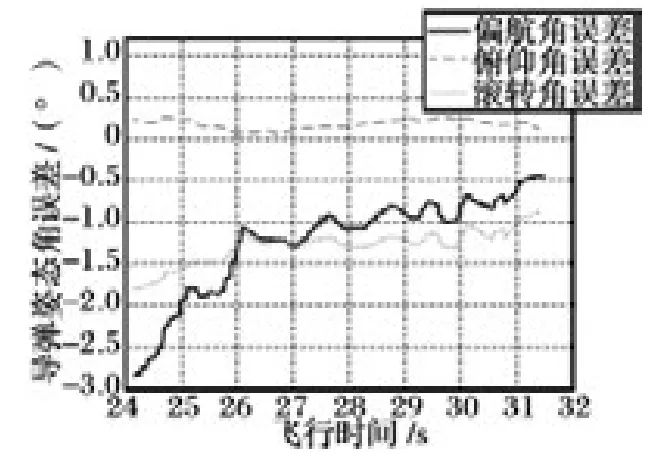
图5 导弹姿态角偏差
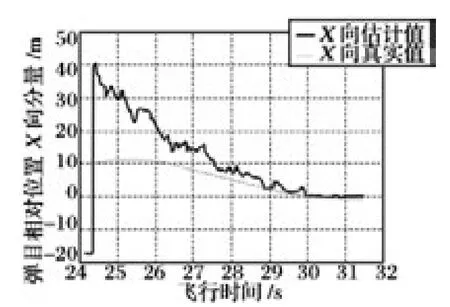
图6 弹目相对位置X 向分量
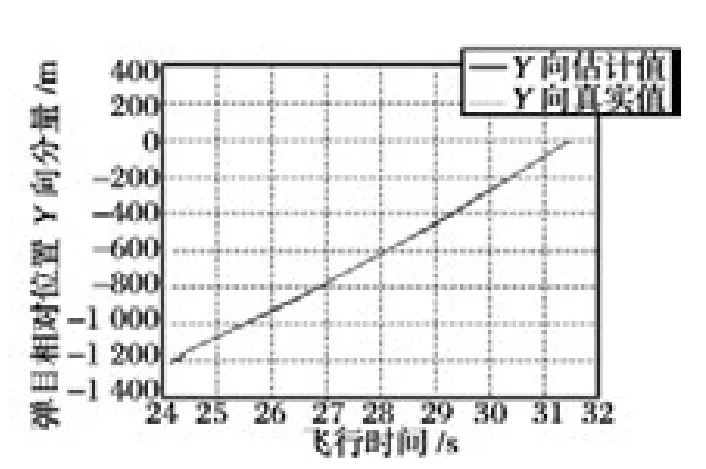
图7 弹目相对位置Y 向分量
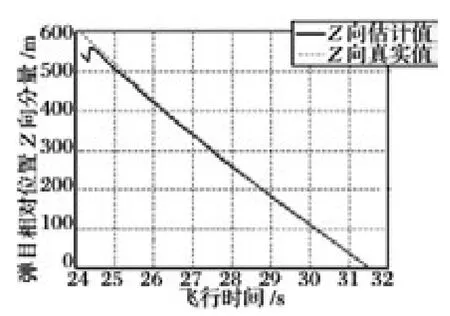
图8 弹目相对位置Z 向分量
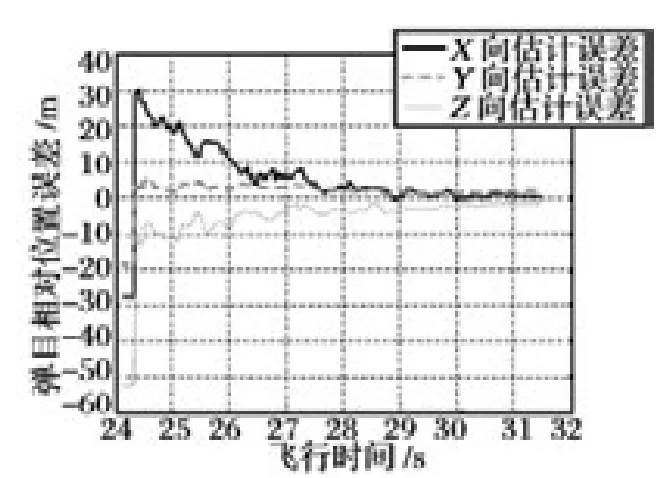
图9 弹目相对位置估计误差
根据图6 ~8 可以看出,按照所提出的算法进行计算能够得到稳定的弹目相对位置(所谓稳定,是指在系统噪声存在的情况下,求得的弹目相对位置不会大范围跳动,即方差过大);同时可以看出,在飞行末端3 s 内,该算法的估计精度在X 向小于3 m,Y 向估计精度在2 m 以内,Z 向精度在4 m 以内。
另外,从图6 ~8 姿态误差的逐渐减小和图9中的估计误差曲线趋势可以看出,导弹姿态误差是影响该算法估计精度的重要因素。
5 结 论
本文对基于捷联导引头测角信息的弹目运动相对位置估计方法进行了研究,主要结论如下:
(1)对于导弹攻击静止目标过程中的弹目相对估计问题而言,由于弹目视线方向与弹目相对速度通常不在一条直线上(若在一条直线上则导弹不需要控制直接攻击目标),此时可以通过利用不同时刻测量弹目相对视线方向构成三角形的方法求解弹目相对位置;
(2)若利用不同时刻测角信息构建三角形对弹目相对位置进行估计,则需要考虑弹目视线方向与弹目相对速度方向夹角较小的情况,此时系统具有弱可观的特性,受系统噪声和测量噪声影响较大;
(3)针对具有弱可观特性的弹目相对位置求解问题,利用截断奇异值求解的方法,可以获得较为稳定的弹目相对位置,并且牺牲的系统无偏性误差在可以接受的范围内;
(4)该算法受姿态误差的影响较大,在使用时,需要对导弹姿态误差对估计精度的影响进行分析;
(5)本文没有考虑测量野值对算法的影响,针对存在野值情况时对算法的进一步改进是下一步的研究工作。
[1]焦迎杰,王潇,陈志坚.捷联寻的制导技术在近程制导火箭中的应用[J]. 弹箭与制导学报,2012,32(1):13-17.
[2]苏身榜. 捷联寻的制导技术及其在国外的发展[J].航空兵器,1994(2):45-50.
[3]张跃,褚海荣. 全捷联图像导引头制导的技术特点[J]. 光学精密工程,2014,22(10):2825-2831.
[4]梁彦刚,郝道亮,唐国金. 捷联导引头视线转率估计的交互式多模型样条滤波算法[J]. 国防科技大学学报,2014,36(5):70-74.
[5]贾鑫,罗艳伟,罗丽. 全捷联导引头解耦技术方法[J]. 战术导弹技术,2013(1):77-81.
[6]孙婷婷,储海荣,贾宏光,等. 捷联式光学导引头视线角速率解耦与估计[J]. 红外与激光工程,2014,43(5):1587-1593.
[7]王琪,付书堂. 捷联导引头去耦算法研究[J]. 航空兵器,2012(6):7-9.
[8]王嘉鑫,林德福,祁载康,等. 全捷联导引头隔离度对制导稳定性的影响[J]. 红外与激光工程,2013,42(10):2608-2613.
[9]李富贵,夏群利,祁载康,等. 全捷联导引头寄生回路影响与辨识矫正[J]. 系统工程与电子技术,2013,35(8):1717-1722.
[10]卢波. 病态问题的奇异值分解算法与比较[J]. 测绘信息与工程,2011,36(4):19-22.
