低距离旁瓣雷达系统设计方法综述
2015-11-15范红旗
吴 灏,范红旗,付 强
(国防科学技术大学ATR 实验室,长沙 410073)
0 引 言
现代雷达系统普遍采用脉冲压缩技术实现大作用距离和高距离分辨力,即在发射端通过发射宽脉冲提高发射的平均功率,以确保最大作用距离;同时在接收端采用脉冲压缩技术获得窄脉冲,以提高距离分辨力[1]。然而随着雷达工作环境的日益复杂,强杂波、干扰、多路径等因素严重降低了雷达的性能。在这些制约因素下,利用传统波形和匹配滤波器的输出会产生较高的距离旁瓣,导致强目标旁瓣遮蔽弱目标或多路径干扰,严重影响弱小目标检测。低距离旁瓣雷达系统设计则是有效克服这些影响进而提升探测性能的有效途径,也是当前国内外雷达界所广泛关注的一项极具挑战性的课题,具有重要的学术意义和极大的军事应用价值。
1 低距离旁瓣雷达系统设计内容
低距离旁瓣雷达系统设计是有效克服复杂环境下强杂波、干扰、多路径等因素进而提升雷达性能的有效途径。低距离旁瓣雷达系统设计主要包含相位编码波形设计、自适应滤波器设计以及波形与滤波器联合设计三方面内容。
(1)相位编码波形设计
相位编码波形以其良好的低截获特性,越来越多地应用于现代雷达系统中。采用相位编码波形通过数字相关器,可实现匹配滤波处理。因此,设计具有良好自相关属性的相位编码波形,能有效抑制距离旁瓣。
(2)自适应滤波器设计
传统雷达系统通常采用固定发射波形或按照给定的工作模式发射周期信号,因此接收滤波器的设计对系统性能有重要影响。最直接的匹配滤波器只能在点目标和白噪声环境下抑制距离旁瓣。针对复杂环境,需要根据回波中的信息自适应地设计滤波器实现脉冲压缩,完成对距离旁瓣的抑制。
(3)波形与滤波器联合设计
某些场景下单靠波形设计或滤波器设计难以达到理想的性能。同时考虑发射端和接收端,对相位编码波形和自适应滤波器联合优化,具有更高的设计自由度,能在复杂环境下最大程度地实现距离旁瓣的抑制。
下文将着重研究相位编码波形设计、自适应滤波器设计和波形与滤波器联合设计,并展望研究趋势。
2 低距离旁瓣雷达系统设计方法
2.1 相位编码波形设计
随着雷达系统对低截获概率(Low Probability of Intercept,LPI)需求的不断提高,相位编码波形以其良好的LPI 特性,被运用于越来越多的雷达系统中。相位编码波形通过数字相关器实现脉冲压缩,但波形的距离旁瓣会严重影响雷达对目标的检测性能,特别是在强杂波、强干扰环境下的弱小目标检测。因此,设计具有良好自相关特性的相位编码波形成为亟待解决的问题。
相位编码波形的设计思路可分为两类:第一类是基于传统频率调制信号,如线性调频(Linear Frequency Modulated,LFM)波形,得到相应的相位编码波形。LFM 是最常见的一种波形,具有低旁瓣、多普勒容限大的特性。波形可表示为x(t)=exp(jπBt2/T),0≤t≤T,其中:B 为带宽;T 为脉宽。以ts=n/B,n=1,…,N(N=BT)采样可得N个采用点,用s(n)表示为
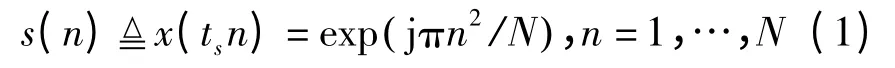
将式中的相位改写为
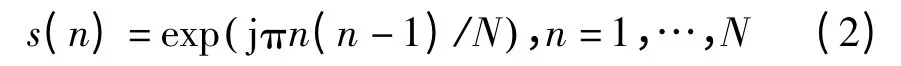
即得到Golomb 码[2]。同样基于LFM 波形,P4码[3]定义为
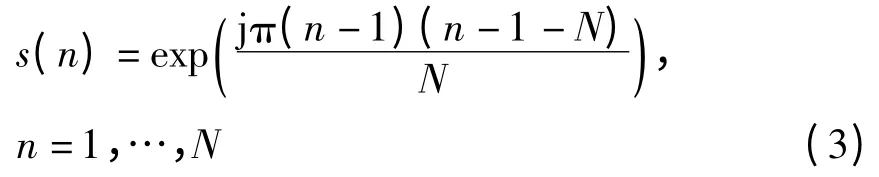
此外,基于二次相位变化的编码还有P3 码,Frank码,Chu 码等[3]。评价自相关函数的准则主要有三个:积分旁瓣电平(Integrated Sidelobe Level,ISL),峰值旁瓣电平(Peak Sidelobe Level,PSL)和加权积分旁瓣电平(Weighted Integrated Sidelobe Level,WISL)。上述几种多相编码波形都具有较好的ISL和PSL。对于二相编码,雷达系统中最重要的编码是巴克码。码长为N 的巴克码峰值旁瓣电平为主瓣的1/N,但N 最大只能取13。采用伪随机噪声序列可以产生更长的二相码,伪随机序列长度约束为N=2P-1(P 为整数),同时峰值旁瓣电平为-10logN[4]。
第二类设计思路是通过优化方法设计相位编码波形。文献[5]利用遗传算法对二相编码波形进行优化设计,文献[6]采用模拟退火法优化设计,两种算法均能产生自相关和互相关性能优良的编码组。然而,这两种算法都是随机进化算法,搜索方向任意迭代次数多,导致收敛慢且运算量大。
2009年,Stoica Petre 等人在文献[7]中创造性地提出了基于快速傅里叶变换(Fast Fourier Transform,FFT)的循环迭代算法CAN,该算法以最小化ISL 为设计准则,实验结果表明算法运算速度快且占用内存低。需要说明的是,循环算法主要运算量为FFT 和逆傅里叶变换(IFFT),能用于长码元的优化,即使在普通PC 上,运算速度也很快,极有可能在工程上首先实现。
图1 比较了码长为100 的几种不同相位编码波形的自相关函数(Auto Correlation Function,ACF)。由图可知,Golomb 和Frank 编码波形基于LFM 信号,自相关函数旁瓣特性接近。随机相位编码波形由于码元相位随机,未经优化,旁瓣性能较差。CAN 编码波形以随机相位编码为初始值,以最小化积分旁瓣电平为准则优化设计,整体自相关函数旁瓣性能最好,尤其是在主瓣周围的区域。
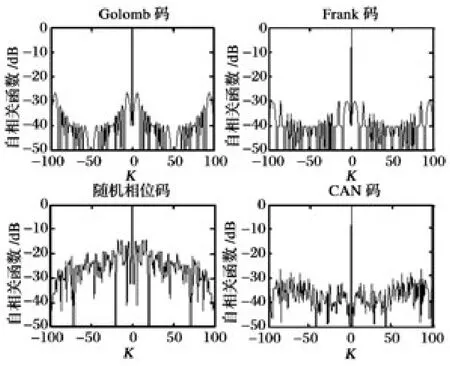
图1 不同相位编码波形自相关函数对比
在CAN 算法基础上,文献[7]又提出了以最小化加权积分旁瓣电平为准则的WeCAN 算法,该算法能产生在指定距离单元具有极低旁瓣的波形,能有效抑制多路径干扰、强散射体对弱小目标的旁瓣遮蔽等。但是,WeCAN 算法由于引入了加权矩阵,算法复杂度较高,不利于在工程上实现。
针对这一问题,文献[8]给出了基于功率谱拟合的优化算法,同样能产生特定距离单元低旁瓣的波形,相比于WeCAN 算法性能更好,且计算时间和内存开销大大降低。同时,考虑到在实际工程中的适用性,优化波形能够满足恒模和低峰均比约束。
图2 比较了采用WeCAN 算法和文献[8]中基于功率谱拟合算法性能。可以看出,文献[8]产生的波形在特定距离单元旁瓣能达到-300 dB 以下,对距离旁瓣遮蔽和多路径干扰有显著抑制效果。
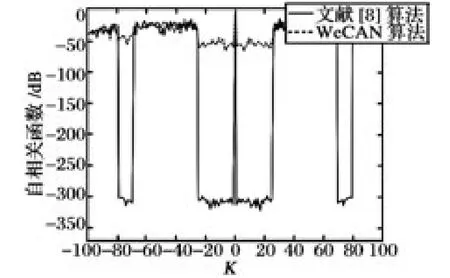
图2 特定区间低旁瓣相位编码波形性能对比
为满足系统大带宽要求的同时对抗同频窄带干扰,设计频谱约束下的低距离旁瓣波形是近年来波形设计领域的另一个研究热点。
文献[9-10]分别提出遗传算法及粒子群优化算法得到稀疏频谱波形,但是运算复杂度高且收敛速度慢。文献[11]引入了权重系数均衡功率谱密度和自相关函数的性能,并建立了联合目标函数。文献[12]给出了功率谱密度和自相关函数两者在稀疏频谱波形设计中的关系。
文献[13]提出了基于最速下降的算法,能生成频谱约束下的低距离旁瓣波形。该算法沿梯度方向搜索,但迭代步长计算复杂且算法复杂度与码长二次方相关。文献[14]提出了以联合最小化频谱阻带能量和积分旁瓣电平为准则的SCAN 算法,算法产生的波形同时具有稀疏频谱和低距离旁瓣的特性。
文献[15]在文献[14]的基础上,提出了基于FFT 的循环迭代算法CIA,并扩展至MIMO 雷达。CIA 算法以联合最小化波形实际功率谱密度PSD和期望PSD 之间的均方误差以及积分旁瓣电平为目标函数,并采用基于FFT 的快速算法求解。图3给出了CIA 算法和SCAN 算法的功率谱密度性能对比,图4 给出了两种算法的自相关函数性能对比。由图可知,CIA 算法产生波形的功率谱陷波更深,能更好满足频谱约束,与此同时整体距离旁瓣电平较SCAN 算法更低,在对抗窄带多径干扰及旁瓣遮蔽方面有明显优势。
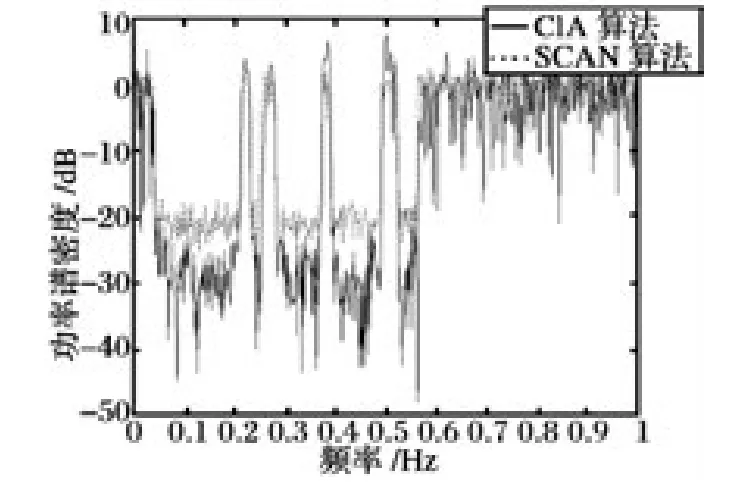
图3 功率谱密度性能对比
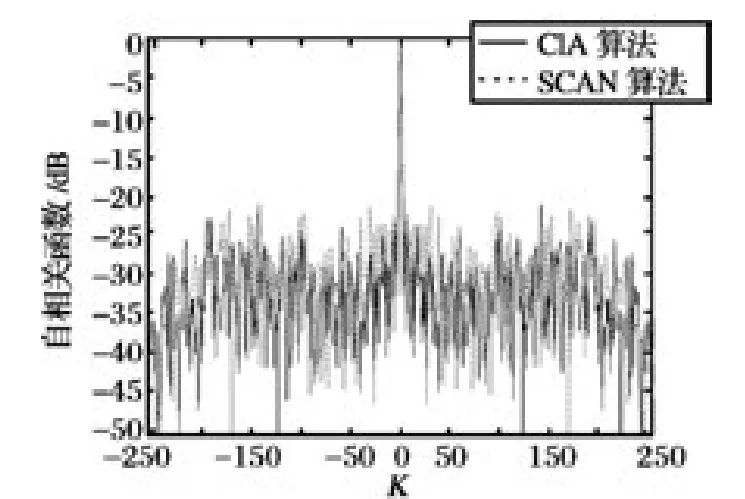
图4 自相关函数性能对比
2.2 自适应滤波器设计
雷达系统中普遍采用脉冲压缩技术来同时获得大作用距离和高距离分辨力,其中最简单的方法是匹配滤波,但该方法只适用于白噪声条件下的点目标场景。对于存在杂波及干扰环境,匹配滤波受到波形模糊函数的约束限制,会产生较高的距离旁瓣,并在后面的恒虚警处理中抬高静态噪声电平,影响检测性能。为更好地抑制距离旁瓣,不同学者提出了不同的滤波器设计方法。
文献[16]给出了失配滤波器的方法,失配滤波器以一定的信噪比损失为代价对旁瓣进行抑制。然而该方法只能在特定发射波形条件下获得较好的低距离旁瓣性能,降低了雷达的低截获能力。
文献[17]提出了最小平方法(LS),通过对相邻距离单元去耦合来实现距离旁瓣的抑制,LS 算法同时优化了峰值旁瓣电平和积分旁瓣电平,但该方法对距离窗外的散射点无法实现有效提取。
为了进一步抑制旁瓣,雷达接收机需要对回波进行自适应脉冲压缩。文献[18]基于加权最小平方提出了IAA 算法,该算法同样通过对邻近距离单元去耦合实现了距离旁瓣的抑制。
Shannon 在文献[19]中创造性地提出了基于最小均方误差(Mean-Square Error,MSE)准则的自适应脉冲压缩算法RMMSE,该算法首先利用匹配滤波获取距离像并作为迭代的先验信息,然后通过迭代算法自适应地抑制距离旁瓣,只需迭代三次即可实现低距离旁瓣,进而实现对小目标的有效提取。
在文献[19]基础上,文献[20]提出了基于最大输出信噪比(MSN)准则的自适应脉冲压缩算法RMSN,同样具有很快的收敛速度。
图5 直观给出了不同算法滤波结果对比。假设发射波形采用的是P4 码,且在第50个距离单元存在目标。由于P4 码具有较高自相关旁瓣,采用匹配滤波方法产生的距离旁瓣最高,峰值旁瓣电平在-20 dB 左右;采用RMMSE 及RMSN 两种自适应脉冲压缩方法大幅削弱了距离旁瓣,峰值旁瓣电平在-70 dB 左右,能有效解决强目标对邻近距离单元的旁瓣遮蔽问题。需要指出的是,RMMSE算法需要迭代3 次,RMSN 算法只需迭代2 次。
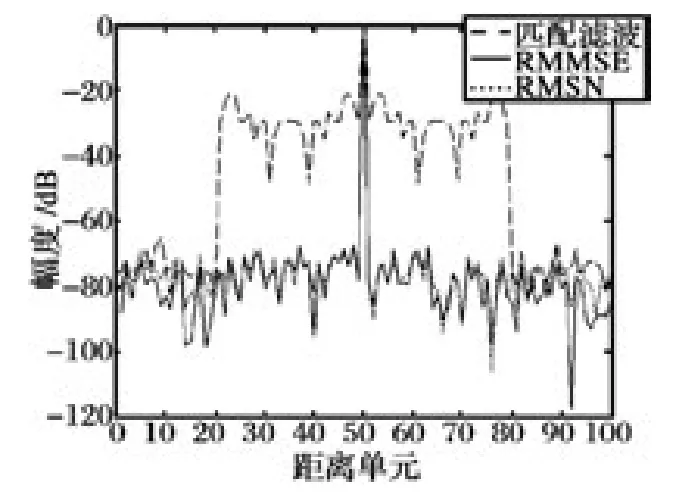
图5 不同算法滤波结果对比
表1 总结了不同滤波方法的各项性能。其中匹配滤波和LS 算法都是非自适应的算法,RMMSE和RMSN 算法利用先验目标匹配滤波距离像信息作为迭代初始值,实现自适应处理。实际应用中,当回波模型为单散射点模型表示且信噪比不高时,可用匹配滤波;当回波模型为多散射点模型表示或信噪比很高时,可用LS 算法;当在接收窗外存在强散射点,且目标场景动态变化时,用RMMSE 或RMSN 算法自适应迭代处理,对旁瓣的抑制效果要明显优于匹配滤波和LS 算法。
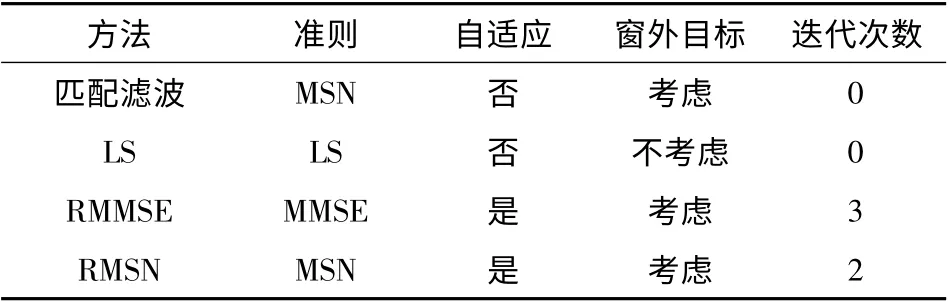
表1 不同滤波器算法性能比较
2.3 波形与滤波器联合设计
在强杂波或干扰环境下,仅靠发射端的波形设计或接收端的自适应滤波器设计,难以达到理想的距离旁瓣性能需求。结合对环境的认知,联合优化发射波形和接收滤波器,是近年来的又一研究热点[21-25]。从设计的角度出发,发射波形、接收滤波器联合优化,具有更高的设计自由度,从而能实现更好的距离旁瓣抑制效果。
针对联合设计波形及滤波器这一难题,各国学者展开了如下研究。
文献[21]以最小化积分旁瓣电平为准则,联合优化得到二相编码波形和滤波器。文献[22]在最大增益损失约束下,以最小峰值旁瓣电平为准则,迭代优化求得最优波形和滤波器。
文献[23]基于杂波及干扰的先验信息,以最小化估计目标散射系数均方误差为准则,提出了CREW 算法,联合设计波形及滤波器。仿真结果表明,在干扰条件下,联合设计相比于只设计波形的CAN 算法以及设计失配滤波器方法,性能有很大提升。文献[24]在文献[23]的基础上提出了一种基于分式规划的快速算法,将时间复杂度降低了一个量级。
文献[25]结合认知雷达设计思想,通过发射探测信号获取接收窗外距离单元散射点的幅度估值,然后利用该信息设计具有低旁瓣的相位编码波形,最后根据散射中心幅度统计信息做自适应滤波处理,很大程度上抑制了距离旁瓣,并实现了从发射到接收的闭环反馈。
为直观给出联合优化的优势,假设雷达工作频段内存在强窄带干扰,干信比为10 dB,强干扰信号会导致较高的距离旁瓣。图6 给出了只优化发射波形和采用CREW 算法联合优化的输出结果对比。

图6 存在强干扰时滤波器输出结果对比
从图6 可以看出,由于干信比很高,仅靠相位编码波形设计,距离旁瓣抑制性能较差;而采用相对复杂的联合优化设计,旁瓣下降了约20 dB,能最大程度地抑制距离旁瓣,有效避免了强散射体对弱小目标的距离旁瓣遮蔽。实际中,可根据目标场景复杂程度,选择是否利用联合波形滤波器优化设计,以获得更好的距离旁瓣抑制效果。
3 结 束 语
本文回顾并探讨了低距离旁瓣雷达系统设计中的相位编码波形设计、自适应滤波器设计以及波形与滤波器联合设计等方法。综述给出的波形设计方法针对的是雷达发射机,滤波器设计方法针对的是雷达信号处理机,这在雷达系统中属于两个截然不同的组件,本身不具有可比性;而波形与滤波器联合设计需要实现从雷达接收机到发射机的闭环反馈,抑制距离旁瓣遮蔽及多路径干扰效果最好,但系统代价也最高。实际应用中要根据具体需求来灵活选择设计方法。
需要说明的是,前文叙述的三种方法产生的都是离线的波形和滤波器,至于需要抑制距离单元的信息如何获得,以及如何真正用于具体的雷达系统,即在线波形设计,这些实际应用的问题都有待进一步研究。同时,如下几个问题还很少被提及:(1)杂波及干扰环境等先验信息的获取;(2)通过对环境的认知智能选择发射波形和相应的滤波器;(3)针对MIMO 雷达系统的联合波形滤波器设计。因此,低距离旁瓣雷达系统设计下一步的研究可以从以下三个方面开展:
a. 通过发射探测信号或其他手段,实时获取并更新杂波及干扰参数。
b. 根据环境信息,进行在线波形及滤波器优化设计,完成接收机到发射机的闭环反馈。
c. 设计基于MIMO 雷达的低距离旁瓣系统,利用MIMO 雷达波形分集技术,进一步提高检测性能。
[1]丁鹭飞,耿富录,陈建春. 雷达原理[M].3 版. 西安:西安电子科技大学出版社,2002.
[2]Zhang Nan,Golomb S W. Polyphase Sequence with Low Autocorrelation[J]. IEEE Transaction on Information Theory,1993,39(3):1085-1089.
[3]He Hao,Li Jian,Stoica P. Waveform Design for Active Sensing Systems:A Computational Approach[M]. Cambridge:Cambridge University Press,2012.
[4]Richards M A.雷达信号处理基础[M]. 邢孟道,王彤,李真芳,译.北京:电子工业出版社,2008.
[5]陶海红,廖桂生. X 波段单发多收体制下用于解距离模糊的时变二相码波形优化设计[J]. 宇航学报,2005,26(5):657-662.
[6]Deng Hai. Polyphase Code Design for Orthogonal Netted Radar Systems[J]. IEEE Transaction on Signal Processing,2004,52(11):3126-3135.
[7]Stoica P,He Hao,Li Jian. New Algorithms for Designing Unimodular Sequences with Good Correlation Properties[J]. IEEE Transaction on Signal Processing,2009,57(4):1415-1425.
[8]Wu Hao,Song Zhiyong,Fan Hongqi,et al. Designing Sequence with Low Sidelobe Levels at Specified Intervals Based on PSD Fitting[J]. Electronics Letters,2015,51(1):99-101.
[9]Liu Weixian,Lu Yilong,Lesturgie M. Optimal Sparse Waveform Design for HFSWR System[C]// International Waveform Diversity and Design Conference,2007:127-130.
[10]Wang Guohong,Lu Yilong. Sparse Frequency Transmit Waveform Design with Soft Power Constraint by Using PSO Algorithm [C]// IEEE Radar Conference,2008:1-4.
[11]Wang Guohong,Lu Yilong. Sparse Frequency Waveform Design for MIMO Radar[J]. Progress in Electromagnetics Research B,2010,20(1):19-32.
[12]Wang Guohong,Lu Yilong. Sparse Frequency Waveform Design Based on PSD Fitting[C]// International Conference on Acoustics Speech and Signal Processing,2011:2860-2863.
[13]Wang Guohong,Lu Yilong. Designing Single/Multiple Sparse Frequency Waveforms with Sidelobe Constraint[J]. IET Radar Sonar and Navigation,2011,5(1):32-38.
[14]He Hao,Stoica P. Waveform Design with Stopband and Correlation Constraints for Cognitive Radar[C]// International Workshop on Cognitive Information Processing ,2010:1-5.
[15]庄珊娜,贺亚鹏,朱晓华. 低距离旁瓣稀疏频谱波形相位编码设计[J]. 电子与信息学报,2012,34(5):1088-1095.
[16]Blinchikoff H J. Range Sidelobe Reduction for the Quadriphase Codes[J]. IEEE Transaction on Aerospace and Electronic Systems,2003,39(2):711-718.
[17]Zrnic B,Zejak A,Petrovic A,et al. Range Sidelobe Suppression for Pulse Compression Radars Utilizing Modified RLS Algorithm[C]// IEEE Inernational Symposium on Spread Spectrum Techniques and Applications,1998:1008-1011.
[18]Yardibi T,Li Jian,Stoica P,et al. Source Localization and Sensing:A Nonparametric Iterative Adaptive Approach Based on Weighted Least Squares [J]. IEEE Transaction on Aerospace and Electronic Systems,2010,46(1):425-443.
[19]Blunt S D,Gerlach K. Adaptive Pulse Compression via MMSE Estimation[J]. IEEE Transaction on Aerospace and Electronic Systems,2006,42(2):572-584.
[20]张劲东,王海青,朱晓华,等. 基于最大输出信噪比准则的自适应脉冲压缩[J]. 电子与信息学报,2009,31(4):790-793.
[21]Stoica P,Li Jian,Xue Ming. Transmit Codes and Receive Filters for Radar [J]. IEEE Signal Processing Magazine,2008,25(6):94-109.
[22]何学辉,吴兆平,苏涛,等. 任意相位编码信号及其脉压滤波器联合优化设计[J]. 西安电子科技大学学报,2009,36(6):1027-1033.
[23]Stoica P,He Hao,Li Jian. Optimization of the Receive Filter and Transmit Sequence for Active Sensing [J].IEEE Transaction on Signal Processing,2012,60(4):1730-1740.
[24]Soltanalian M,Tang Bo,Li Jian,et al. Joint Design of the Receive Filter and Transmit Sequence for Active Sensing[J]. IEEE Signal Processing Letter,2013,20(5):423-426.
[25]吴旭姿,刘峥,刘韵佛. 杂波环境下发射-接收联合优化的自适应滤波方法[J]. 电子与信息学报,2013,35(11):2657-2663.
