Optimizing reliability,maintainability and testability parameters of equipment based on GSPN

Tingpeng Li,Yue Li,Yanling Qian,and Yongcheng Xu

Science and Technology on Integrated Logistics Support Laboratory,National University of Defense Technology,Changsha 410073,China

1.Introduction

Reliability,maintainability and testability(RMT)are important design parameters of equipment.RMT parameters affect not only the property and capability of the equipment,but also the life cycle costs(LCC).

In recent years,some progress has been made on determination of RMT parameters.Liu[1]proposed a method to determinate reliability indexes,which integrates experience of similar equipment,requirements of users and capability of suppliers.In[2],a method of determination of reliability parameters based on the constraint of LCC was presented.Quality function deployment(QFD)was introduced in[3]to determine maintainability parameters.Li[4]established a maintainability evaluation model to evaluate schemes of maintainability based on grey relational analysis.With the results of evaluation and repeated attempts,designers can get proper testability parameters.The genetic algorithm(GA)was proposed to determine system testability indexes in[5,6].Zhang[7]proposed a method to select testability parameters on the basis of modified analytic hierarchy process,whereas this method did not discuss how to determine the values of parameters.Qian[8]introduced generalized stochastic Petri nets(GSPN)to define system-level testability parameters.However,he only established the relationship between operational availability and testability parameters without other constraints(e.g.cost constraint)considered.On the other hand,only testability parameters can be obtained through repeated analysis on the relation curves of availability and testability parameters.Ding[9]proposed a system of RMT parameters which can be divided into three levels:tactics,techniques and engineering design.However,the method for how to determine parameters was not discussed.

Jonge presented a method to determine the maintenance strategy based on lifetime distribution,which is assumed to obey Weibull distribution[10].Saranga studied the application of probabilistic maintenance models to determine the optimal inspection rates considering the tradeoff between reliability and cost[11].Tian developed a physical programming based approach to tradeoff between cost and reliability[12].Kim estimated the condition-based maintenance parameter based on the continuous time Markov process and the EM algorithm[13].Jeang optimized the design and maintenance parameter(interval time)considering LCC of the product[14].

However,most of these existing works mentioned above only focus on one of the RMT properties(e.g.[1–6]),and very few consider all of them synthetically.Besides,though the method of selection of RMT parameters is introduced in some papers,there is no discussion on how to determine the values of the parameters(e.g.[7,9]).Moreover,most of the existing methods are based on the history data of similar equipment or experts’experiences,but seldom consider the effects of RMT on the operation process(e.g.[3,5]).

In this paper,a new method is proposed to determine RMT parameters.This method considers not only the history data of similar equipment and experts’experiences,but also the effects of RMT on the operation process.

2.Problem description

RMT parameters are proposed in the design phase,and have significant effects on the operation process of equipment.For example,mean time between faults(MTBF),an important reliability parameter,affects the continuous working time without faults.Therefore,this paper takes the operation process of equipment into account to determine RMT parameters.

Generally,equipment can be categorized into two types:continuous working equipment and intermittent working equipment.This paper focuses mainly on continuous working equipment whose work time is much longer than MTBF,such as communication equipment(e.g.radar).In addition,the equipment,whose down time without faults is very short,could also be viewed as continuous working equipment.

2.1 The operation process of equipment

Continuous working equipment has only two states:working and under maintenance.Maintenance falls into preventative maintenance and corrective maintenance.

Preventive maintenance consists of on-condition maintenance and scheduled maintenance,and corrective maintenance consists of accurate maintenance and fuzzy maintenance.Accurate maintenance means motivated maintenance with successful results of faults detection and diagnosis,while fuzzy maintenance means exploratory maintenance when faults detection or diagnosis fails.

The operation process of continuous working equipment is shown in Fig.1.The equipment works normally for most of the time.However,whenever faults occur,the equipment has to be stopped to be detected and diagnosed.If faults detection and diagnosis are successful,the equipment will recover to work immediately after accurate maintenance.Otherwise,fuzzy maintenance must be executed.In addition,on-condition maintenance will be conducted when the states of the equipment satisfy the conditions of preventive maintenance.

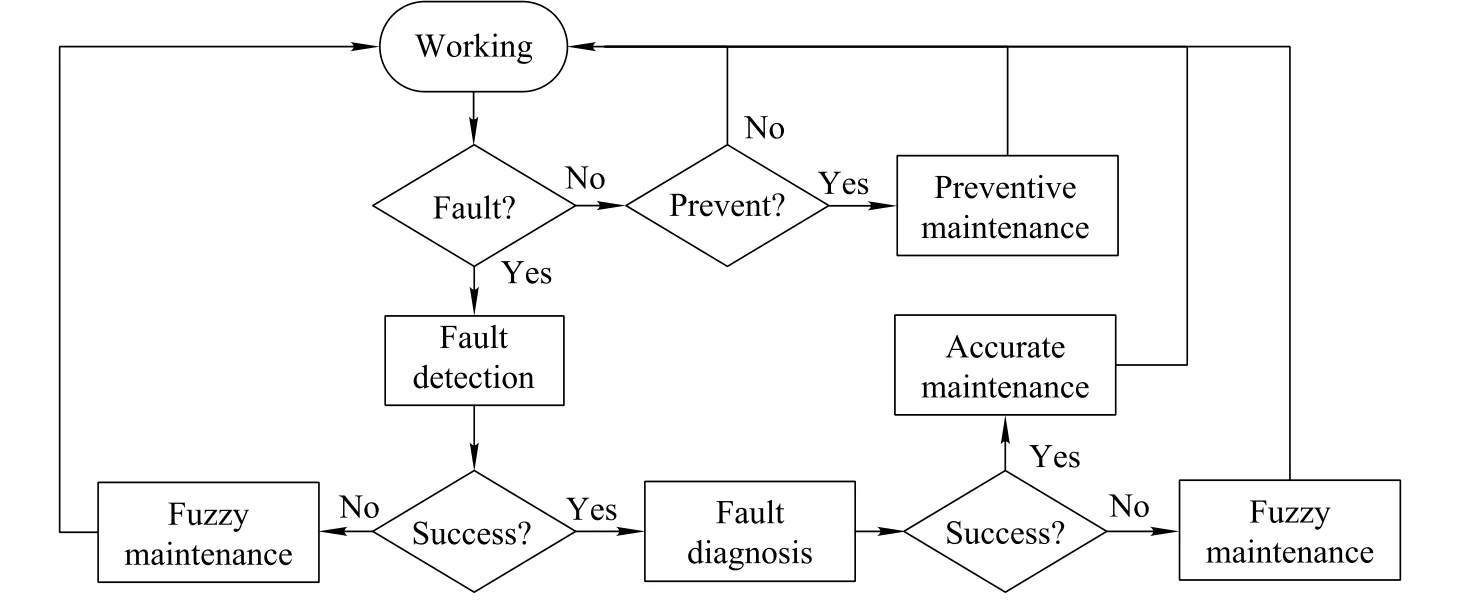
Fig.1 Operation process of continuous working equipment

2.2 RMT parameters of equipment

Reliability is the ability to complete required functions under specified conditions and within stipulated time[15].Equipment reliability consists of basic reliability and mission reliability[16].Basic reliability stands for the failurefree probability under specific conditions within a period of time.Mission reliability is the ability to complete prescribed tasks.In the design phase,designers mainly consider the basic reliability of equipment.Therefore,the most important parameter of basic reliability,i.e.MTBF,is the mainly considered reliability parameter in this paper.Generally,MTBF can be divided into preventive mean time between faults(PMTBF)and never preventive mean time between faults(NPMTBF).PMTBF is the mean time between faults which can be maintained preventively,and NPMTBF means the mean time between faults which can only be maintained after occurring.If the failure rate of equipment obeys the exponential distribution,the relationship among the three parameters is shown as follows:

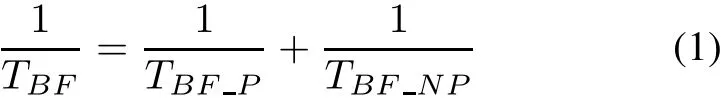
whereTBFis MTBF,TBFPis PMTBF,andTBFNPis NPMTBF.

Maintainability means the ability to be maintained or repaired in a specified state according to prescribed procedures and methods[15].Mean time of accurate maintenance(TAM),mean time of fuzzy maintenance(TFM)and mean time of preventive maintenance(TPM)are main parameters of maintainability.

Testability is a design characteristic which represents the ability to determine its states timely and accurately and to diagnose its faults effectively[17].This paper chooses four most important factors as testability parameters:faults detection rate(Pd),fault isolation rate(PI),faults detection time(Td)and fault isolation time(TI).The faults detection rate is the ratio between the number of detected faults and the total number of faults in a period.The fault isolation rate is the ratio between the number of isolation faults and the number of detected faults.Faults detection time means the mean time of faults detection per time.And fault isolation time is the mean time of faults isolation per time.

RMT parameters of equipment considered in this paper are shown in Table 1.

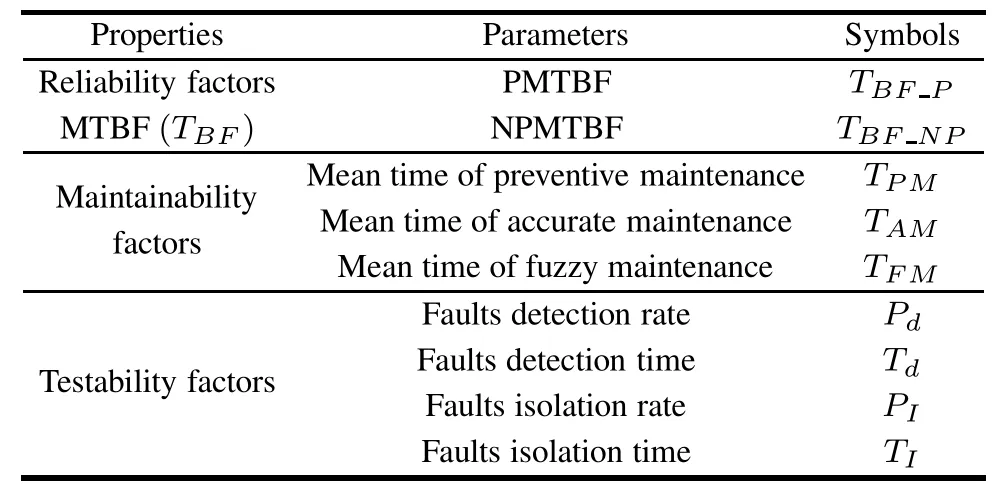
Table 1 RMT parameters of equipment

2.3 Assumptions

The operation conditions of equipment are usually complex,and different equipment has different operation characteristics.To focus on the key point,some assumptions are made as follows:

(i)MTBF,faults detection time,fault isolation time and maintenance time are assumed to obey the exponential distribution.

(ii)The mean time between preventive maintenance is assumed to be as the same as PMTBF,which means the lead time of preventive maintenance is ignored.

(iii)All the human factors are ignored.

3.Solution

As mentioned before,most design characteristics will affect the operation process of equipment in the operation phase.Therefore,taking the operation process into consideration is beneficial for determination of RMT parameters.Thus,we firstly establish the GSPN model of the operation process based on the operation flow of equipment.Afterwards,by solving the GSPN model,the quantitative relationship between operational availability and RMT parameters is obtained.Besides,the cost model can be built based on the life time and the history data of similar equipment.With costs,operational availability and available ranges of parameters considered,the determination and optimization model of RMT parameters can be established.Finally,the appropriate RMT parameters will be calculated though solving the model with some calculation tools,such as Matlab.The detail flow of the solution is shown as Fig.2.

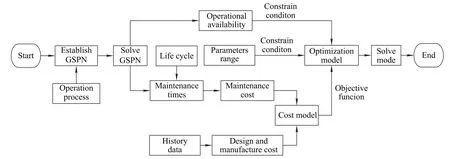
Fig.2 Workflow of optimizing RMT parameters of equipment

3.1 The GSPN model of operation process

The concept of GSPN is derived from stochastic Petri nets(SPN),and it extends timed and immediate transition conceptions[18].GSPN can be defined algebraically as follows[19]:

A GSPN is an 8-tuple,GSPN=(P,T,A,V,S,B,W,M0),whereP={P1,P2,...,Pm}is a finite set of place;T={T1,T2,...,Tn}is a finite set of transitions,including timed transitions and immediate transitions;A⊆(P×T)∪(T×P)is a set of arcs;Vis a forbidden arc;Sis the fire rate of timed transitions;Bis activation probability of immediate tensions;Wis a weight function that takes values 1,2,3,...,andM0is the initial marking.

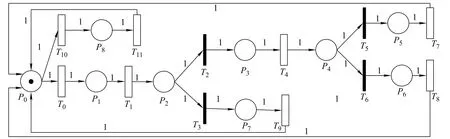
Fig.3 GSPN model of the operation process of continuous working equipment

GSPN is used in many application fields for the validation and evaluation of distributed systems which characterized by concurrency,synchronization and congestion[21,22].Compared with SPN,GSPN not only needs fewer calculation costs but also has the ability to model indeterminacy processes[23–25].In the operation process of equipment,some tasks,such as faults detection and diagnosis,are indeterminacy processes.Therefore,GSPN can be chosen to model the operation process of equipment.

According to the operation flow of continuous working equipment which is shown as in Fig.1,the GSPN model of the operation process is established and shown in Fig.3.

In the GSPN model shown as Fig.3,the places denote the states of the equipment and the physical meaning of each place is shown in Table 2.

Table 2 Physical meanings of places

In the GSPN model shown in Fig.3,immediate transitions mainly model the results of work which contains two different possibilities.Timed transitions mainly model physical work,such as faults detection,diagnosis and maintenance.

Most of the working time in this operation process is stochastic variable.For example,the accurate maintenance time is determined by the occurring faults modes,while the faults modes occur randomly.In addition,for most continuous working equipment,it is reasonable to assume that the working time obeys exponential distribution and the parameter of the exponential distribution is the inverse of the mean time parameter,described as

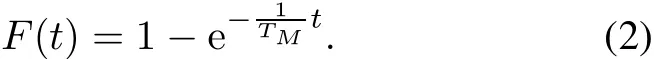
whereF(t)is the distribution function of the working time,andTMis the mean time of working per time.

The physical meanings and parameters of all transitions of the GSPN model are shown in Table 3.

In Table 2,the parameters of immediate transitions mean the probability of being fired,and the parameters of timed transitions are the inverse of the mean time.

Table 3 Physical meanings and parameters of all transitions

3.2 The solution of GSPN model

Simulation and mathematical analysis are the two main methods to analyze the GSPN model.The simulation method employs computer technology to analyze the statistic results of the GSPN model,e.g.stochastic Petri net package(GPNP)is one of the widely used simulation anal-ysis software which was developed by America Duke University.The mathematical analysis method employs mathematical theory to get properties of the GSPN model.For example,the qualitative relationships between parameters and probability of stability can be obtained based on continuous time Markov process(CTMP)theory[23].Since we need to establish an optimization model,the qualitative relationship is crucial to achieve this.The mathematical analysis method is chosen to solve the GSPN model in this paper.

3.2.1 Reachability graph and state-transition matrix

All mathematical analysis methods are based on the theorem that the reachability graph of GSPN is isomorphic to a CTMP[26],and the reachability graph is the key point for mathematical analysis.Therefore,the reachability graph of the GSPN model should be obtained at first.

The reachability graph of the GSPN model consists of states and the relationships among states.Based on the GSPN model of continuous working equipment(shown in Fig.3),the states of the model are defined and shown in Table 4,whereMi(i=0,1,...,8)are the reachable states of the GSPN model andPi(i=0,1,...,8)are places of the GSPN model.The relationships among states can be directly got from the GSPN model.Thus we can obtain the reachability graph of the continuous working equipment,as is shown in Fig.4.

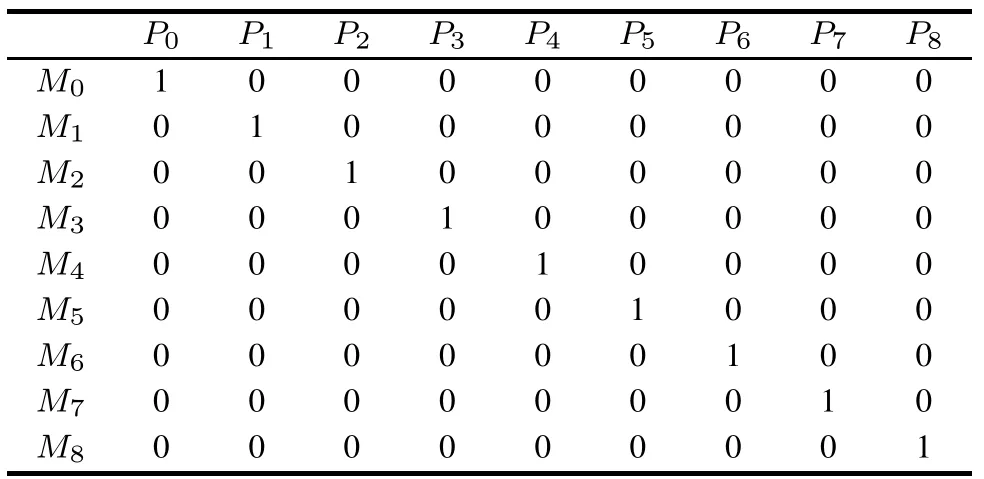
Table 4 States of GSPN model of continuous working equipment

In the reachability graph of the GSPN model,states can be classified into virtual states and actual states[26].Virtual states refer to the states which connect with other states via immediate transitions.The remaining time of virtual states is zero.In order to simplify the calculation of CTMP,the virtual states should be removed from the reachability graph.According to the definition of virtual states and the GSPN model,M2andM4are virtual states.The simplified reachability graph is shown in Fig.5.

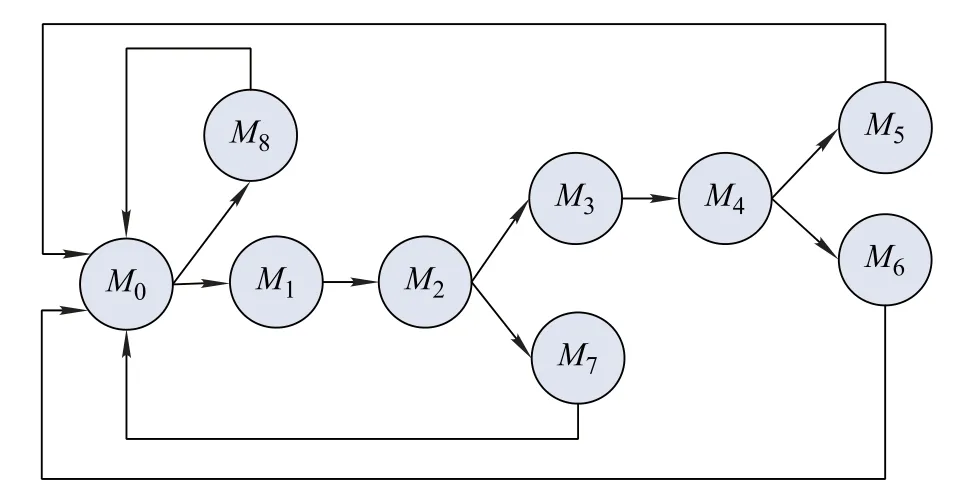
Fig.4 Reachability graph of the continuous working equipment

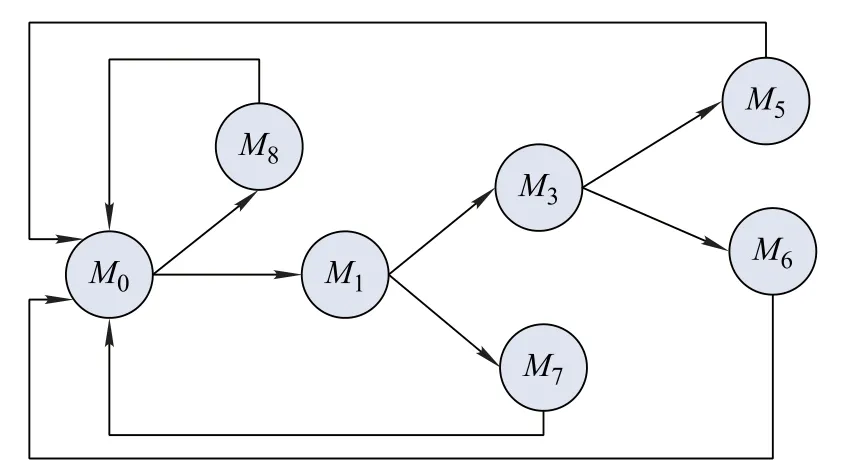
Fig.5 Simplified reachability graph of continuous working equipment

According to the transition parameters(shown in Table 1)and the simplified reachability graph(shown in Fig.5),the state-transition matrix(P)can be calculated directly and is shown as(4).Pijdenotes the mean speed of transition from stateito statej.For example,the mean speed of transition fromM0toM1is 1/TBFNP.In addition,since the transition probability of each state is 1 and the transition speed obeys exponent distribution,the sum of elements of each row is zero:

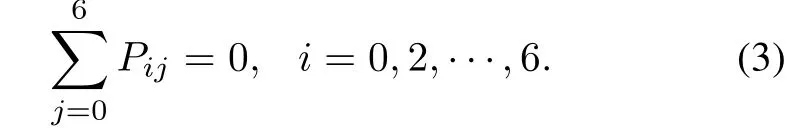
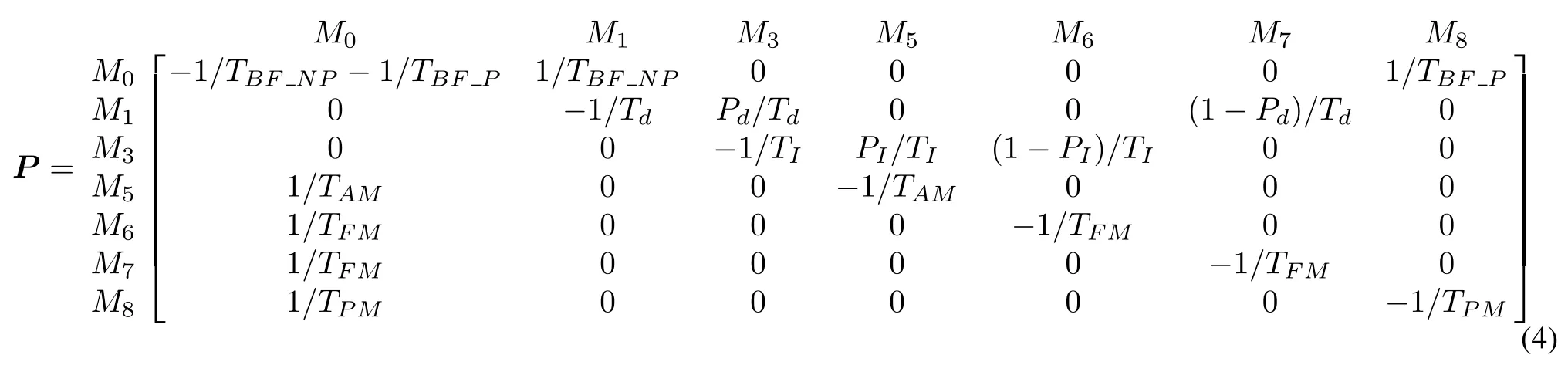
3.2.2 Probability of stability

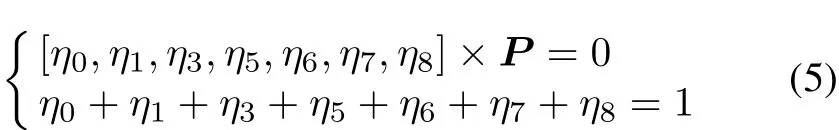
According to the basic characteristic of CTMP[27],probabilities of stability of all states must satisfy the following equation:whereΠ=[η0,η1,η3,η5,η6,η7,η8]contains the probabilities of stability ofMi(i=0,1,3,5,6,7,8)andPdenotes the state-transition matrix of CTMP.

By solving(5),all the probabilities of stability can be obtained and shown as(6).

3.3 Optimization model of RMT parameters

To build an optimization model,it needs to determine constraint conditions and objective functions.Operational availability is important to evaluate the integrated property of equipment.Therefore,operational availability is a constraint condition.Besides,every RMT parameter should be limited in a reasonable range to make the results of optimization acceptable.As always,high quality and low price are two aspects of desired properties in the design phase.However,higher quality usually comes with higher cost.So,we choose the costs of equipment as the objective function.

3.3.1 Operational availability

The operational availabilityA0is the ratio between the available working time and the total life time.A0is an integrated parameter to evaluate the properties of the equipment,especially RMT[27].The operational availability of continuous working equipment is the probability of working states,which means,the operational availability is the probability stability of stateM0.

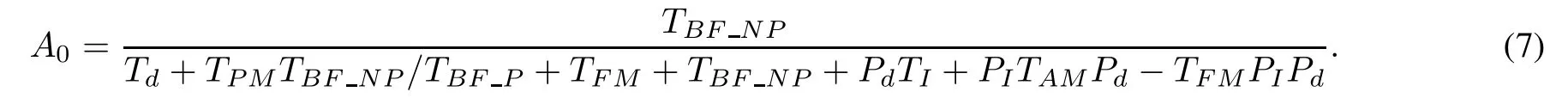
3.3.2 Available range of RMT parameters

RMT are the important design properties of equipment,and each RMT parameter has a special physical meaning.In order to ensure the optimization results of parameters to be acceptable,every parameter should be limited in a certain range,as shown in Table 5.Generally,the ranges of parameters are determined according to that of similar equipment and experts’suggestions.

3.3.3 Cost model

LCC contains all costs from the design phase to the decommission phase.Statistics data show that design costs,manufacture costs and maintenance costs are the main parts of LCC.Recently,some methods have been proposed to establish the cost model of equipment.In[28–30],the gray system theory was introduced to predict the costs ofequipment.The costs prediction model was developed based on support vector machine(LVM)in[31].In[32],the adaptive network-based fuzzy inference system(ANFIS)was used to estimate the costs of avionics equipment.In[33,34],the data processing for the cost model is studied.The parametric method and the analogy method are the two main methods to estimate the costs.The analogy method estimates the costs only based on similar equipment and experts suggestions.The parametric method calculates the costs based on the qualitative relationship between costs and design parameters[35].As the objective function and optimization variable parameter of the optimization model,the qualitative relation of costs and RMT parameters needs to be estimated.Therefore,we choose the parametric method to calculate the costs of the equipment.

Table 5 The ranges of RMT parameters

(i)Design and manufacture costs

No general model for design and manufacture costs exists(CDM),since different equipment has different characteristics.Generally,the qualitative relationship between design parameters and the costs of design and manufacture is established through analyzing the history data of similar equipment.It requires enough history data on design parameters and the costs of design and manufacture.Based on the history data of similar equipment,we choose the least square algorithm(LSA)to estimate the design and manufacture costs.

(ii)Maintenance costs

Statistics show that maintenance costs consume over 60%of LCC[17].Therefore,reducing maintenance costs is significant to reduce LCC.The maintenance costs of continuous working equipment comprise accurate maintenance costs,fuzzy maintenance costs and predictive maintenance costs.

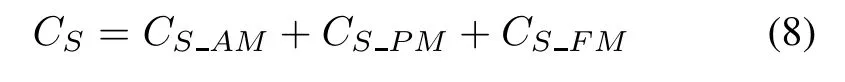
whereCSis maintenance costs,CSAMis accurate maintenance costs,CSFMis fuzzy maintenance costs andCSPMis predictive maintenance costs.

The mean costs per time of maintenance can be calculated based on the history data of similar equipment or experts’suggestions,and the maintenance costs can be calculated with the following equation.

whereKAMis the times of accurate maintenance,KFMis the times of fuzzy maintenance andKPMis the times of preventive maintenance in all the life time.CAMis the costs per time of accurate maintenance,CFMis the costs per time of fuzzy maintenance andCPMis the costs per time of preventive maintenance.

The times of maintenance can be calculated through the following equations:

whereTALAMis the total time of accurate maintenance,TALFMis the total time of fuzzy maintenance andTALFMis the total time of preventive maintenance.Once the design life of equipment is determined,the time of maintenance can be calculated by the following equations:

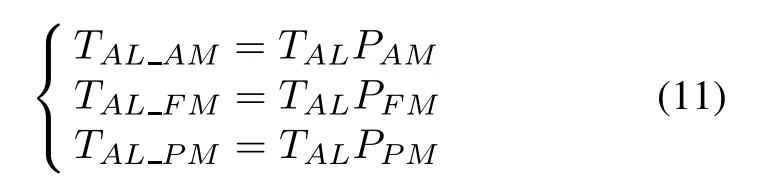
wherePAMis the probability of stability of the accurate maintenance state,PFMis the probability of stability of the fuzzy maintenance state andPPMis the probability of stability of the preventive maintenance state.According to the results of the analysis of GSPN in Section 3.2,the three important probabilities of stability can be calculated with the following equations:

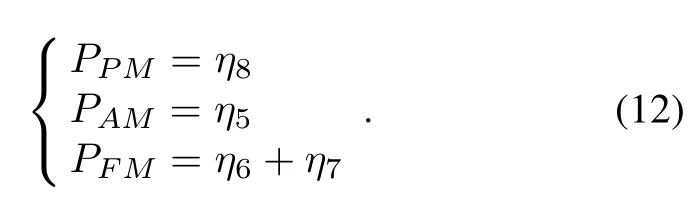
Therefore,

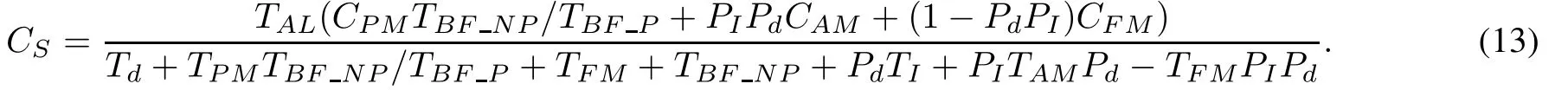
3.4 Solving determination and optimization model

Taking costs of equipment as the objective function and operation availability and available ranges of RMT parameters as constraint conditions,the determination and optimization model of RMT parameters can be established and is shown as(14).In this model,the constraint condition(A0min≤A0≤A0max)and the objective function(CDM+CS)are nonlinear functions.The general method to solve this nonlinear programming problem is the itera-tion algorithm.The first step of the iteration algorithm is to determine an appropriate start point.A better point can be found based on a certain searching algorithm.By iterative computation,the ideal parameters will be found in the end.Generally,the calculated quantity of the solution of the determination and optimization model is rather huge.However,many optimization tools,such as Matlab,Lingo and Mathematic[36–38],have the capability to alleviate it.

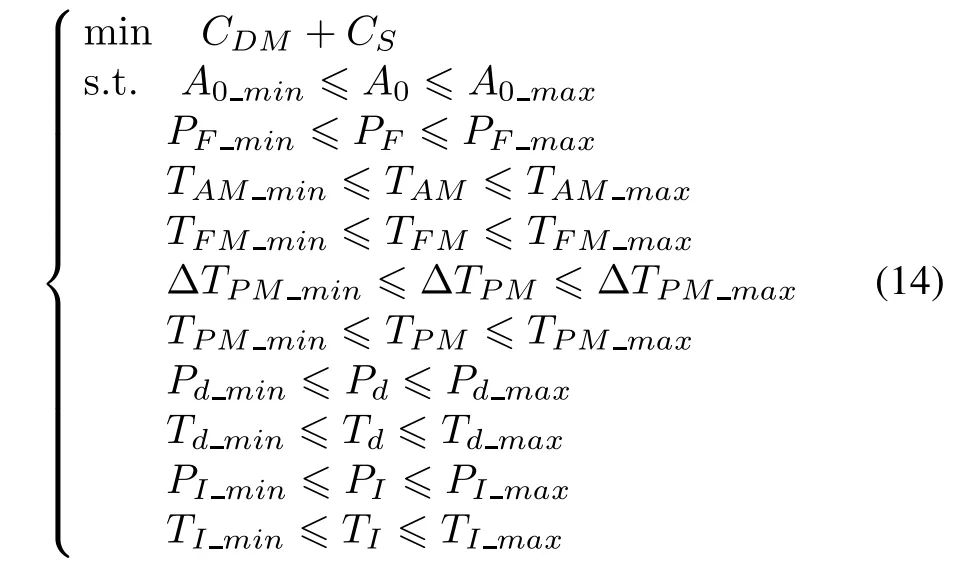
4.Application

To validate the effectiveness and practicability of the proposed approach,we apply it to an example of determination and optimization of RMT parameters of certain equipment.

The operation flow of the equipment is shown in Fig.1 and the GSPN model is shown in Fig.3.

4.1 Costs of the equipment

(i)Design and manufacture costs

The equipment is an improved version of certain equipment.The costs data of the original equipment can be used to modify the design and manufacture costs of the improved equipment.The history data of the original equipment are shown in Table 6.

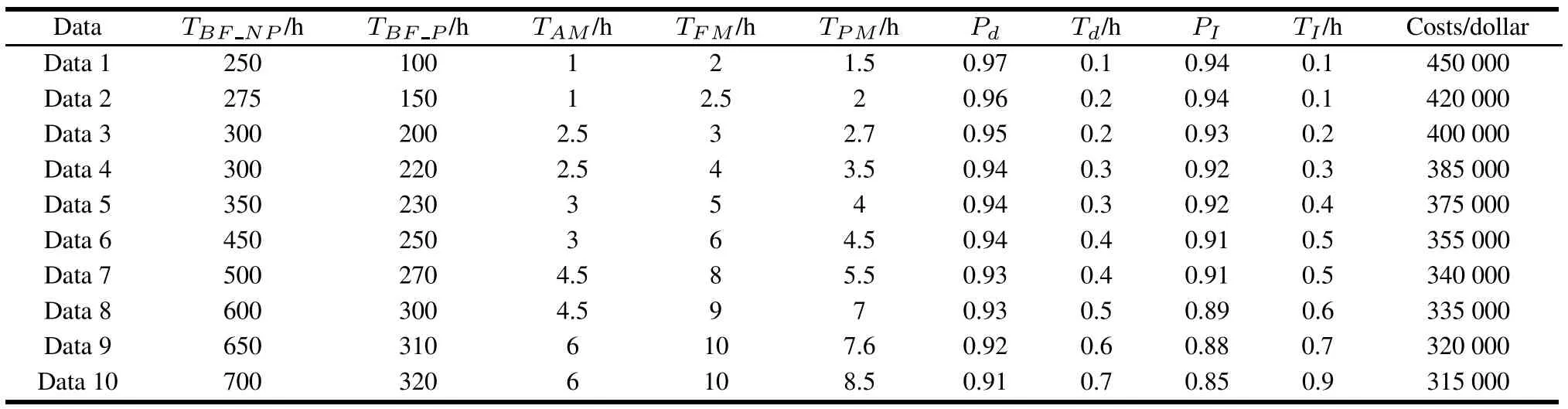
Table 6 Design and manufacture costs of similar equipment with different RMT parameters

Based on the characteristics of similar equipment and experts’suggestions,the cost model is presented as follows:

whereCDMis the design and manufacture costs,andλi(i=1,2,...,9)denotes undermined parameters.

All the undermined parameters can be determined with the Matlab functionnlinfit.The result is shown as follows.

(ii)Maintenance costs

With the statistic results of the costs of accurate maintenance,fuzzy maintenance and preventive maintenance of the similar equipment,the costs per maintenance can be obtained and shown as in Table 7.The design life time of the equipment is 5 000 h.

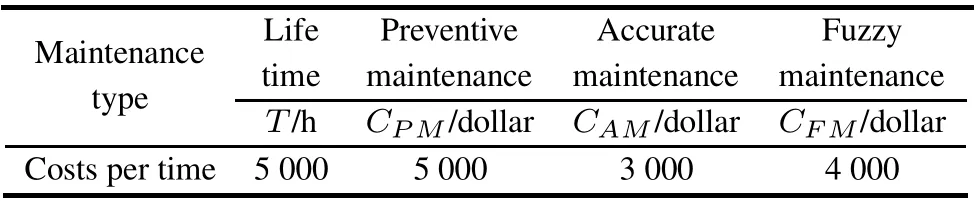
Table 7 The costs per maintenance

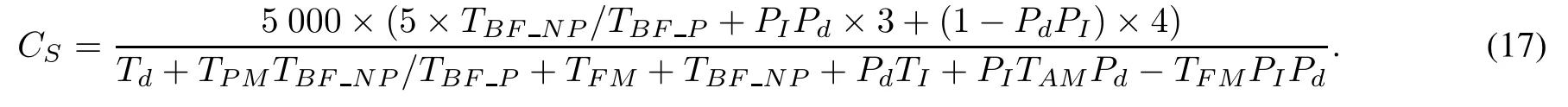
The maintenance cost model can be calculated with(10)and the data are shown in Table 7.The result is shown as follows:

4.2 Optimization model of RMT parameters

(i)Available ranges of RMT parameters

According to the task requirement and suggestions of experts,the available ranges of RMT parameters can be obtained as shown in Table 8.

(ii)Operational availability

Operational availability is an integrated index of RMT properties.According to the task requirement,the operational availability should be over 98%.

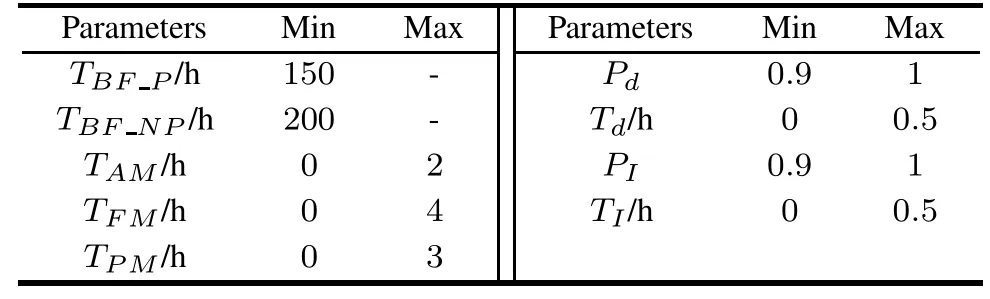
Table 8 The available ranges of RMT parameters

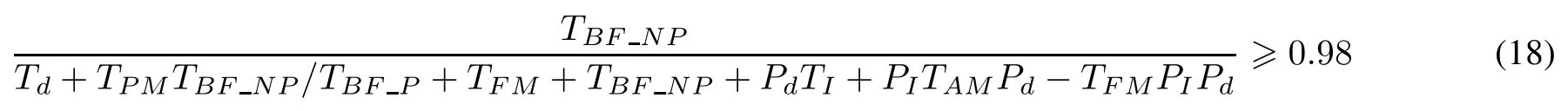
(iii)Determination and optimization model

Taking costs of equipment as the objective function and considering operation availability and available ranges,the determination and optimization model can be established as follows:

4.3 Result of optimization

Many optimization tools can be used to optimize the model.We choose the Matlab optimization tool box to optimize the RMT parameters.With the nonlinear optimization tool and the interior point optimization algorithm,the optimization results are calculated as shown in Table 9.

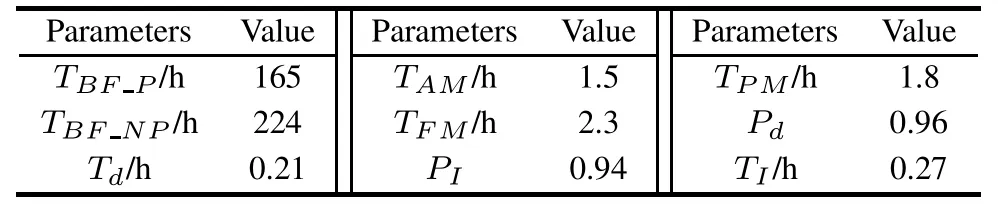
Table 9 The results of RMT parameters

The operational availability,costs and other maintenance data are shown in Table 10.

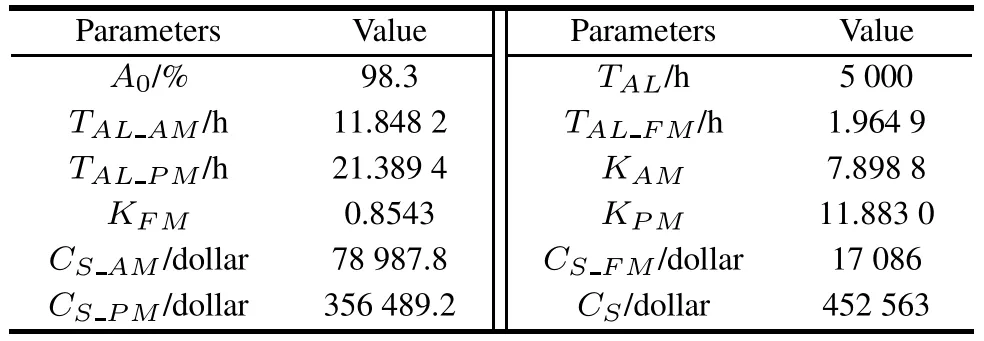
Table 1 0 Operational availability,costs and other maintenance data

As shown in Table 9 and Table 10,all the RMT parameters are determined and the values satisfy operational availability constraint and ranges constraints.Therefore,the method proposed in this paper can be used to obtain the appropriate RMT parameters.In addition,the results of costs can be chosen as an important reference for expense budget of equipment.

Compared with the classical method,such as[1,3,8],the method proposed in this paper has some advantages and are shown as follows:

(i)The influence of RMT parameters on the operation process is adequately considered when determining parameters.

Most of the methods(e.g.[3,6]),proposed to calculate these parameters,are only based on experts’suggestions or experience and do not consider the impact of the parameters on the operation process.While the impact is very important for determining appropriate RMT parameters.

(ii)Reliability parameters,maintainability parameters and testability parameters can be determined and optimized synthetically.

The three properties of equipment have strong dependency on each other and separately determining any of them is difficult to get the accurate results.

(iii)In contrast to qualitative analysis methods,this paper builds a mathematic optimization model and the values of parameters can be obtained,which has significant meaning for engineering projects.

5.Conclusions

RMT are important design properties for equipment.The determination of RMT parameters has impact on not only the capability but also supportability and LCC of the equipment.In addition,the three properties interact with each other deeply and only synthetic determination can get appropriate parameters.

In this paper,a determination and optimization model of RMT parameters is proposed based on the GSPN model of continuous working equipment.Moreover,the effectiveness and practical utility of the model is validated by an example of application.Although the main aim of the model is to determine and optimize the RMT parameters,the intermediate results,such as maintenance costs,can also be an important reference for expense budget of equipment.A limitation of this approach is the assumption that all the random variables obey exponential distribution.To make it more general,in the future this approach will be tested out with different distributions.

[1]J.H.Liu.Reliability indexes determination and proof scheme for wideband tactical radio.Radio Communications Technology,2012,38(1):7–9.

[2]X.J.Ma,H.Q.Zhang.Research on the contribution of reliability index adjustment to LCC of weapon equipment.Equipment Manufacturing Technology,2013,2013(7):52–86.

[3]P.F.Guo,H.Z.Zhang,C.F.Yu,et al.Design requirements for construction machinery maintainability based on QFD.Science ＆ Technology Review,2011,29(34):49–53.

[4]F.Li,Y.Yang,J.J.Yang.Integrative evaluation on parameters of maintainability design of mechanical equipment.Journal of Engineering Design,2008,15(2):11–15.

[5]X.M.Lu,K.L.Huang,G.Y.Lian,et al.Research on deciding testability figures of complicated equipment.Computer Measurement ＆ Control,2008,16(3):357–359.

[6]J.X.Li,G.Liu,P.Di.Research oil testiability index allocation method of warship equipment.Ship Electronic Engineering,2012,32(6):108–109.

[7]Y.S.Zhang,K.L.Huang,G.Y.Lian.Research on selection of testability parameters of missile based on modified AHP.Computer Measurement ＆ Control,2011,2012(2):412–414.

[8]Y.L.Qian,J.Qiu,X.S.Wen.Generalized stochastic petri network for defining the systme-level testability parameters and figure of figure of merit.Systems Engineering and Electronics,2002,24(5):4–7.(in Chinese)

[9]D.H.Ding,J.Lu.Discussion on the system of reliability,maintainability and supportability parameters.Journal of China Academy of Electronics and Information Technology,2011,06(2):171–174.(in Chinese)

[10]B.de Jonge,W.Klingenberg,R.Teunter,et al.Optimum maintenance strategy under uncertainty in the lifetime distribution.Reliability Engineering and System Safety,2015,(133):59–67.

[11]K.Saranga.Application of probabilistic maintenance models for selecting optimal inspection rates considering reliability and cost tradeoff.Transactions on Power Delivery,2014,29(1):178–186.

[12]Z.G.Tian,D.M.Lin,B.R.Wu.Condition based maintenance optimization considering multiple objectives.Journal of International Manufacture,2012,(23):333–340.

[13]M.J.Kim,V.Makis,R.Jiang.Parameter estimation in a condition-based maintenance model.Statistics and Probability Letters,2010,(80):1633–1639.

[14]A.Jeang.Optimal parameters design and maintenance interval for a product with quality and cost considerations.Proc.of the Institution of Mechanical Engineers,Part B:Journal of Engineering Manufacture,2014,(223):737–747.

[15]General Reserve Department of PLA.Terms of reliability,maintainability and testability,2005.

[16]Y.X.Qing.Overview of reliability,maintainability and testability.Beijing:National Defense Industry Press,2002.

[17]J.Qiu.Model and design technology of equipment testability.Beijing:Science Press,2012.

[18]H.T.Wang,F.He,H.G.Xiong.Modeling of avionics blueprint architecture based on GSPN and LP.Aerospace Science and Technology,2013,(26):111–119.

[19]G.Thangamani.Availability analysis of a Lube oil system using generalized stochastic Petri net.Proc.of the IEEE International Conference on Quality and Reliability,2011:186–189.

[20]E.G.Amparore.A new great SPN GUI for GSPN editing and CSLTAmodel checking.Proc.of the 11th International Conference on Quantitative Evaluation of Systems,2014.

[21]C.Eisentraut,H.Hermanns,J.P.Katoen,et al.A semantics for every GSPN.Proc.of the 34th International Conference of Petri Nets,2013:90–109.

[22]G.Balbo,M.Beccuti,M.De Pierro,et al.First passage time computation in tagged GSPNs with queue places.The Computer Journal,2011,54(5):653–673.

[23]R.Y.Al-Jaar.Performance evaluation of automated manufacturing systems using generalized stochastic Petri nets.New York,1989.

[24]H.Zhan.Study of the normal generalized stochastic Petri nets and its application in testing system.Proc.of the Instrumentation and Measurment Technology Conference,2006.

[25]S.A.Reveliotis,Y.C.Jin.A generalized stochastic Petri net model for performance analysis and control of capacitated reentrant lines.IEEE Trans.on Robotics and Automation,2003,19(3):474–480.

[26]J.Y.Zhang.Modularized modeling and reliability analysis of manufacture systems based on GSPN ＆ ESPN.Shenyang:Northeastern University,2007.

[27]Z.C.Xu.Engineer and management of equipment supportability.Beijing:National Defense Industry Press,2006.

[28]C.J.Wang.Research of costs of missile based on gray predictive model.Ship Electronic Engineering,2007,27(2):134–136.

[29]M.Y.Yang,M.Z.Shen.Study on the estimation of the engine development cost based on the gray combined model.Mathematics in Practice and Theory,2006,36(10):161–166.

[30]Y.Wang,F.Liu,P.Y.Zhang,et al.Prediction model of airforce equipment maintenance and support cost based on gray system theory.Mathematics in Practice and Theory,2012,42(9):137–141.

[31]J.Y.Zhu,X.B.Zhang,H.X.Zhang,et al.Multi-parameter equipment cost estimation based on a support vector machine.Systems Engineering and Electronics,2003,25(6):701–703.(in Chinese)

[32]J.Y.Zhu,J.F.Yu,H.X.Zhang.The application of ANFIS network in the study of the cost estimation of avionics equipment.Systems Engineering and Electronics,2002,24(3):57–60.(in Chinese)

[33]Y.J.Zhao,M.Liu.Data diagnosis and recognition of costs parameter model of weapon system.Aerospace Shanghai,2000,2000(2):43–45.(in Chinese)

[34]Y.J.Zhao.Data processing for the weapon types’cost parameter model.Aerospace Shanghai,2001,(5):18–20.(in Chinese)

[35]S.Zhang,Y.G.Chen.Three development costs estamitation models based on paramter method.Journal of Sichuan Armaments Factories,2010,31(3):53–56.

[36]M.L.Zhang.Computer implementation of solving of nonli-near programming problem.Journal of Armed Police College of Engineering,2006,22(2):5–9.

[37]C.T.Yu,F.C.Li.Operations research.Beijing:Science Press,2006.

[38]W.H.Chao,Z.Guo.Optimization method and MATLAB implementation.Beijing:Chemical Industry Press,2005.