Ensemble feature selection integrating elitist roles and quantum game model

Weiping Ding,Jiandong Wang,Zhijin Guan,and Quan Shi

1.College of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;

2.School of Computer Science and Technology,Nantong University,Nantong 226019,China;

3.Provincial Key Laboratory for Computer Information Processing Technology,Soochow University,Suzhou 215006,China

1.Introduction

Recently,both the number and the dimensionality of datasets in many large-scale real-world applications have sharply increased,and lots of irrelevant and redundant data not only complicate the problems,but also degrade the accuracy of solutions.The challenge is how to transform data into information,and information into knowledge.As an important step of data pre-processing,feature selection aims to provide a minimal feature subset from the problem domain,which retains a boosted accuracy in representing the original features[1].

As one of the effective feature selection methods,the rough set theory(RST),one of the granular computing(GrC)methods,is a valid mathematical theory to deal with uncertain,imprecise and vague information[2,3].Attribute reduction in RST offers a systematic theoretic framework for feature selection,which attempts to retain the discerning ability of original features for the objects from the universe,so it has been successfully applied in feature selection[4–7].

Based on RST,the state-of-the-art algorithms of feature selection consist of two categories:one is under algebra representation,and the other is under information representation.Under algebra representation,feature selection algorithms mainly include the positive region based algorithm,discernible matrix based algorithm and improved discernible matrix based algorithm.Under information representation,feature selection algorithms mainly include the information entropy based algorithm,the conditional information entropy based algorithm and the mutual information based algorithm[4,5].However,when dealing with large-scale real-world datasets,these algorithms tend to be time-consuming and inefficient,and ratio of misclassification is higher.The computational cost for feature selection is quite expensive.Therefore,it is necessary to further investigate some effective and efficient heuristic algorithms from other unique perspectives.

The game theory is a mathematical theory of socioeconomic phenomena exhibiting interactions among decision makers[8].The quantum game,as the combination of quantum computation and the game theory,is very different from the classical game theory,and also has been a new growing interest.Eisert et al.firstly introduced the famous prisoner’s dilemma into quantum domain based on the maximally entangled state[9].Meyer applied quantum strategies to the traditional matching pennies game and showed the player who implemented the quantum strategy could increase his expected payoff[10].Sun et al.presented the quantum market game of generalizing evolutionaryN-player Bertrand’s model with partial information entanglement between two adjacent firms[11].Ahmed et al.discussed the quantum team games and replicator dynamics of the quantum prisoner’s dilemma game[12].These recent developments in quantum games motivate us to study how to design some novel quantum game mechanisms and strategies,and apply them into the implementation of feature selection.

To accelerate the process of feature subset selection,we propose an efficient ensemble elitist roles based quantum game(EERQG)algorithm for feature selection to find a minimal feature subset with the Pareto optimum equilibrium.The feasibility and effectiveness of EERQG is evaluated on extensive University of California,Irvine(UCI)machine learning datasets for some feature selection and classification tasks.Experimental results show EERQG can greatly improve the efficiency and accuracy of feature selection.

The main contributions of this paper can be described as follows:

(i)The multilevel elitist roles based dynamics equilibrium strategy is established,and both immigration and emigration of elitists are able to be self-adaptive to balance between exploration and exploitation for feature selection.The mean of the optimal equilibrium points of multilevel elitist roles is given.

(ii)The utility matrix of trust margins is introduced to the model of multilevel elitist roles to enhance various elitist roles’performance of searching the optimal feature subsets,and the win-win utility solutions for feature selection can be attained.Meanwhile,a novel ensemble quantum game strategy is designed as an intriguing exhibiting structure to perfect the dynamics equilibrium of multilevel elitist roles.The ensemble manner of multilevel elitist roles is employed to achieve the global minimal feature subset.

This paper is organized as follows.Related work is introduced in Section 2.Some preliminaries are given in Section 3.Trust margins based multilevel ensemble quantum game model are presented in Section 4.The proposed EERQG algorithm is described in detail in Section 5.In section 6,some simulation results are discussed.Finally,the conclusions are drawn in Section 7.

2.Related work

As mentioned in Section 1,a considerable amount of theoretic research has been done in the field of feature selection algorithms,and a rich harvest has been obtained.Yang et al.proposed a novel condensing tree structure for rough set feature selection,and then two corresponding heuristic algorithms based on the new feature ordering strategy were used to improve the performance of feature selection[13,14].Parthal´ain et al.presented a new approach based on the tolerance rough set model to explore the boundary region for feature selection[15].Qian et al.proposed an efficient accelerator for feature selection called positive approximation in incomplete information systems in order to characterize the granulation structure of an incomplete rough set using a granulation order[16].Sun et al.constructed the effective uncertainty measures evaluating the roughness and accuracy of knowledge to improve the computational efficiency of feature selection[17].Ding et al.applied a quantum-inspired shuffled frog leaping algorithm to enhance the performance of feature selection,furthermore developed a novel feature selection algorithm based on the hierarchical elitist role model combining competitive and cooperative co-evolution[18,19].Ma et al.presented a heuristic genetic algorithm to feature selection for the decision region distribution preservation,in which a new modified operator was constructed by using two kinds of decision region distribution of condition information contents[20].Qian et al.proposed the parallel feature selection algorithms to parallelize the traditional attribute reduction process based on MapReduce framework,in which a novel structure of＜key,value＞pair was used to speed up the computation of equivalence classes and attribute significance[21].

The game-theoretic rough set(GTRS)is a recent development in RST for analyzing and making intelligent decisions when multiple criteria are involved.It can be well used to analyze region uncertainties defined with an information-theoretic interpretation.Recent researches have investigated GTRS and feature selection.For example,Herbert et al.studied the GTRS model and its capability of analyzing a major decision problem evident in existing probabilistic rough set models,in addition,a learning method using the GTRS model was formulated to analyze payoff tables[22].Sun et al.introduced a cooperative game theory based framework to evaluate the power of each feature,and presented a general filter scheme to handle the feature selection problem[23].Azam et al.used the GTRS model to construct a mechanism for analyzing the uncertainties of rough set regions with the aim of finding effective threshold values[24].

Although most previous feature selection algorithms strive to reduce the redundancy of features while maintaining the discerning ability of original features,they will turn to be computationally impractical when facing exponential computation for large-scale real-world datasets.From the above,the feature selection algorithm proposed from perspectives of GTRS and quantum games has little been discussed.This motivates our study in this paper.

The main difference from aforementioned methods is that we apply an EERQG algorithm to improve the performance of feature selection.The dynamics equilibrium strategy can be self-adapted by both immigration and emigration mechanisms of multilevel elitist roles.Furthermore,the quantum game strategy would perfect the dynamics equilibrium during feature selection,which will be described in the following sections.

3.Preliminaries

To make this paper self-contained,the aim of this section is to introduce some related definitions[2–4],which are the basis of the description of EERQG.

Definition 1In RST,an information system,called a decision table,is defined asS=(U,A,V,f)whereU,called universe,is a nonempty set of finite objects;A=C∪DwhereCis the set of condition attributes andDis the set of decision attributes,Vis a set of values of attributes inA,andf∶U×A→Vis a description function.LetS=(U,A,V,f)be an information system,and everyP⊆Agenerates an indiscernibility relationInd(P)onU.

Definition 2For anyR⊆C,an equivalence relationI(R)is defined as

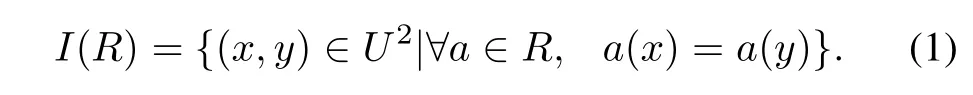
If(x,y)∈I(R),thenxandyare indiscernible by attributes fromR.The equivalence classes ofR-indiscernibility equivalence relationI(R)are denoted as[x]R.

Definition 3For a given subsetR⊆Aand a subsetX⊆U,theR-upper approximationof setXis defined as

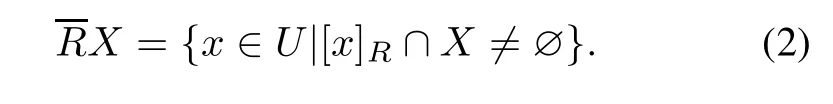
TheR-lower approximationof setXis defined as

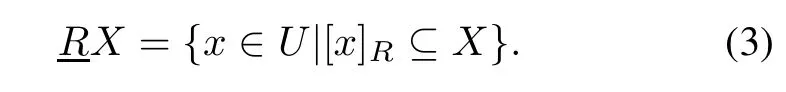
RXis the set of objects ofUwhich can be possibly classified as elements ofXby usingR,where[x]Rrepresents an equivalence class ofInd(P)which containsx.

is the set of all objects fromUwhich can be classified certainly as elements ofXemploying the set of attributesR.They are described in Fig.1.

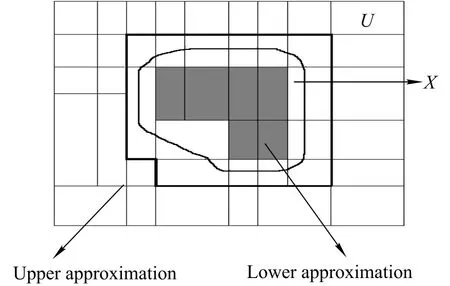
Fig.1 Diagram of upper and lower approximation

Definition 4LetP,Q⊆A,Qdepends onPin a dependency degreek(0≤k≤1),denoted asP⇒kQ,where

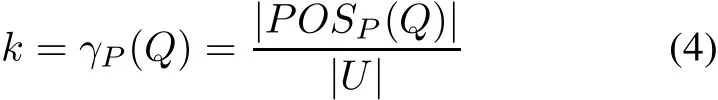
where|•|represents the cardinality of a set,andPOSP(Q),called the positive region,is defined as

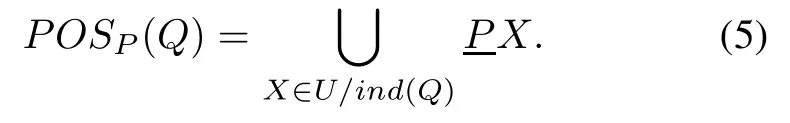
TheP-positive region contains all the objects inUthat can be uniquely classified to blocks of the partitionU/Qemploying attributes fromP.

Definition 5Attribute reductions aim to remove redundant attributes in order that the reduced set can provide the same classification quality as the original.A reduction is defined as a subsetRof the conditional attribute setCasγR(D)=γC(D).A given decision table may have many attribute reductions,and the set of all reductions is defined as

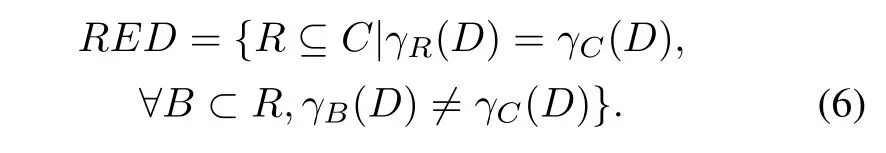
Definition 6A reduction with minimal cardinality attempts to locate a single element of the minimal reduction setREDmin⊆REDas follows:

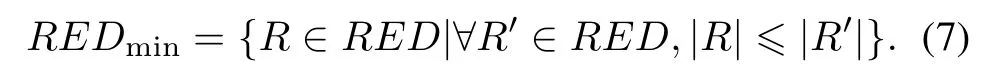
Definition 7The quantum-inspired evolutionary algorithm(QEA)utilizes the concepts of quantum bit(Q-bit),superposition of states and collapse of states.QEA uses Q-bit as a probabilistic representation which has a better characteristic of population diversity than any other representation.Thus the Q-bit individual has a better advantage to represent the linear superposition of states[25,26].

The Q-bit is defined as the smallest unit of information as a pair of complex number(α,β),which is characterized by

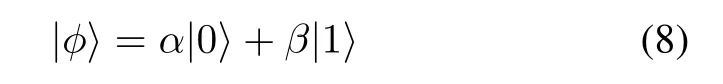
where|0〉and|1〉represent the classical bit values“0”and“1”respectively,andαandβare complex numbers that refer to the probability amplitudes of corresponding states.The parameter|α|2is the probability that the Q-bit will be found in the“0”state,and|β|2is the probability that it will be found in the “1”state.The normalization condition of the state will guarantee|α|2+|β|2=1.

Definition 8The initial quantum individuals are generated by the binary coding method randomly asP(t)=wherenis the scale of evolutionary individuals,and(j=1,2,...,n)is thetth quantum individual,which is defined as follows:

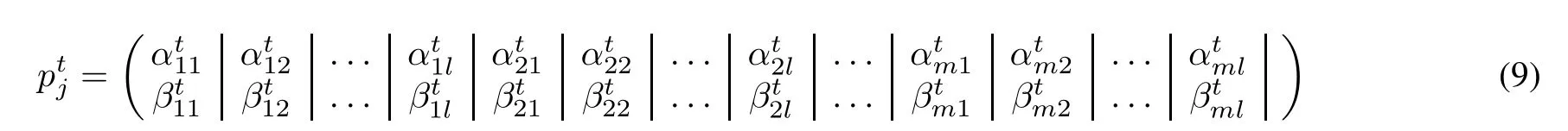
wheremis the number of genes in the chromosome of quantum individuals,andlis the number of quantum bits of each gene.

4.Multilevel ensemble quantum game model based on elitist roles

4.1 Multilevel elitist roles based dynamics equilibrium strategy

In this subsection,the architectures of the multilevel elitist roles based dynamics equilibrium strategy is presented,as described in Fig.2.Through this adaptive dynamic strategy,the equilibrium points of elitist roles can be attained with balancing exploration and exploitation during feature selection,meanwhile both immigration and emigration of elitist roles can be self-adaptive.Evolutionary elitist roles can collaborate for higher profits,and the equilibrium space with the joint decision-making mechanism would achieve the results with optimal profits.

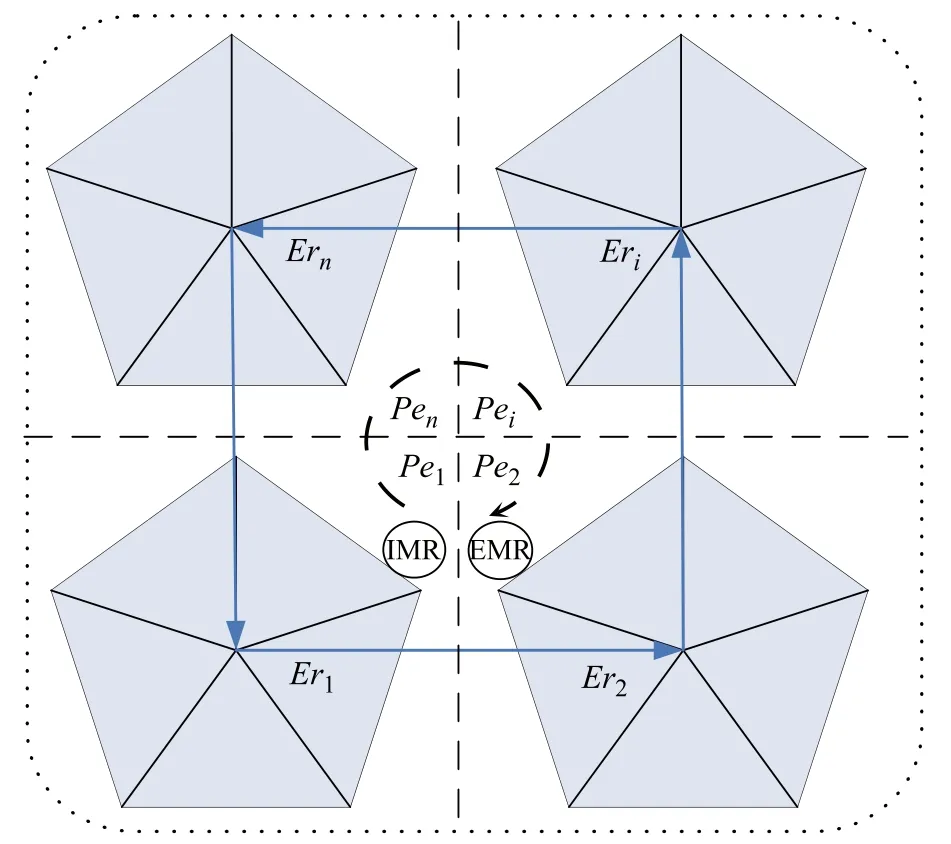
Fig.2 Architectures of multilevel elitist roles based dynamics equilibrium strategy

The main processes of the dynamics equilibrium strategy are described as follows:

Algorithm 1Multilevel elitist roles based dynamics equilibrium strategy

Step 1The evolutionary space is divided into some equal-area pentagons(Pe1,Pe2,...,Pen).All evolutionary populations are grouped in different pentagons by the uniformity.Our projection divides each pentagon into equal-area triangles as described in Fig.2.

Step 2The best fitness individual in each triangle is selected out,named the elitist role.Thus all elitist roles in each pentagon will be generated,and sorted from best to worst.The set of multilevel elitist roles in each different pentagon is formed as follows:

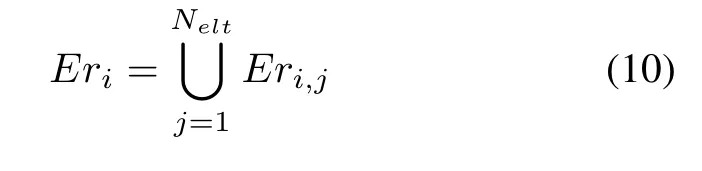
whereNeltis the maximum number of elitist roles.

Step 3Each elitist role inEricalculates its own immigration rateIMRi,jand emigration rateEMRi,jas follows:

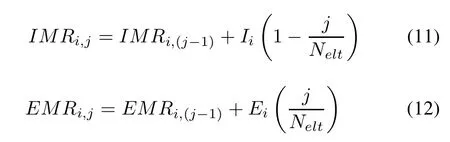
whereIiis the maximum immigration rate of theith pentagon,Eiis the maximum emigration rate of theith pentagon,andjis the sequence number of elitist roles sorted in the set of multilevel elitist roles.

Step 4Multilevel elitist roles would migrate according toIMRi,jandEMRi,j(described as the arrow’s direction in Fig.2)between neighborhood pentagons,thus the archived multilevel elitist roles are updated.

Step 5Ericalculates the whole average fitness value of containing elitist roles,and then the fitness value will be sent to elitist roles in neighborhood pentagons,which will prompt elitist roles to re-evaluate their respectiveIMRi,jandEMRi,j.

Step 6Repeat Step 1 to Step 4 until all elitist roles in pentagons can converge to the dynamics equilibrium.

The global equilibrium points set called mean best(Mbest)of elitist roles are defined as the mean of the opti-mal equilibrium points of multilevel elitist roles.It is constructed as follows:

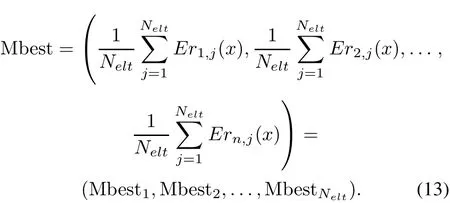
In each pentagon spacePei,the migration of multilevel elitist roles can find the best rate to select elitist roles for the moving.This will result in the ideal multiple independent equilibrium.Thus,multilevel elitist roles will attain the overall optimal equilibrium during the feature selection.Through the above procedures,the dynamics equilibrium strategy can be self-adapted by both immigration and emigration mechanisms of multilevel elitist roles,and the appropriate number of elitist roles is determined to be involved in the following quantum game for feature selection.

4.2 Fitness of multilevel elitist roles

The fitness of multilevel elitist roles is defined as follows:

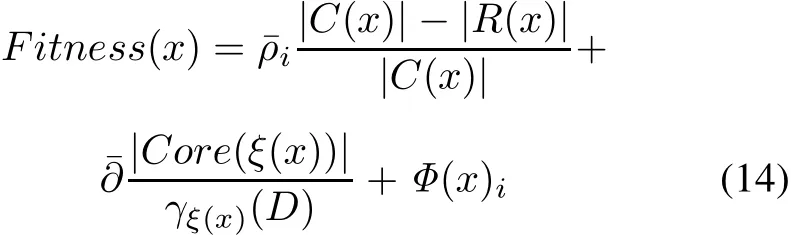
where|C(x)|is the total number of attribute features,|R(x)|is the “1”number of the position or the length of selected attribute subsets,ξ(x)is the attribute subsets,andCore(ξ(x))is the reduction core of feature subsets.γξ(x)(D)is the reduction quality of attribute subsetsξ(x)relative to decision attribute setD.The parameterρi=represents the average fitness of theith pentagon of multilevel elitist roles,and the parameterrepresents the average fitness of total multilevel elitist roles.Φ(x)is an adaptive penalty function and formulated as follows:

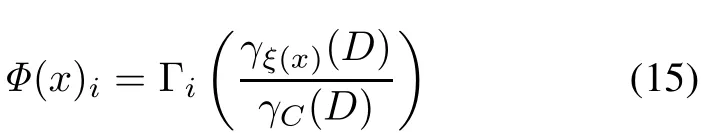
where the parameter Γiis the assign credit value which is defined as follows:

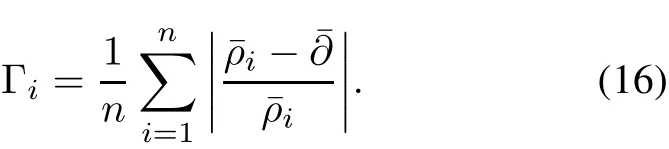
4.3 Utility matrix of trust margins

To determine one elitist role’s remuneration payment to other elitist roles during the process of feature selection,we define the corresponding trust weight of elitist roles as the trust margin(TM)as follows:

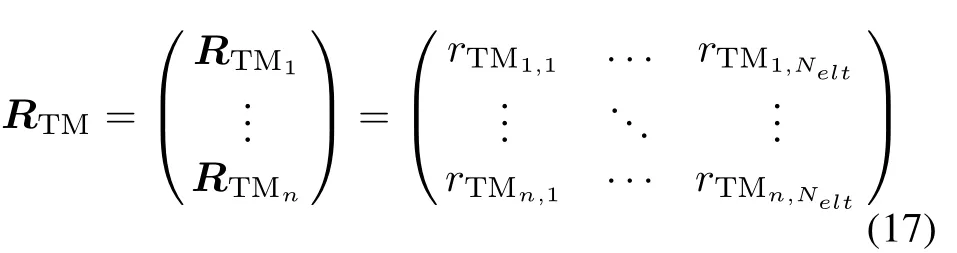
whereRTMi(1≤i≤n)is the trust margin vector of theith pentagon of multilevel elitist roles,andrTMij,TM of thejth elitist role in theith pentagon is defined as

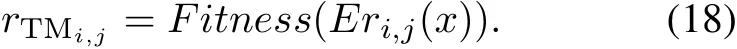
The utility matrix of trust marginRTMwill be used to determine the properties of the superiority of the elitist strategy during the ensemble quantum game.After the dynamic adjustment of trust margins,multilevel elitist roles will form a stable equilibrium.This will enhance various elitist roles’performances of searching the optimal feature subsets in order to achieve the win-win utility solutions for feature selection.

4.4 Ensemble quantum game method of multilevel elitist roles

Multilevel elitist roles will adjust their strategy to better achieve the evolutionary state of stable equilibrium.Based on multilevel elitist roles with generating the utility of trust margins,we extend the classic Eisert’s quantum game model[9]and design an ensemble quantum game method of multilevel elitist roles.Its flowchart is shown in Fig.3.

Kernel steps are detailed as follows.

Algorithm 2Ensemble quantum game method of multilevel elitist roles

Step 1Set up a search space ofDdimensions,and represent each elitist role’s position as the Q-bit chromosome with lengthmgenes by using(9).

Step 2Obtain the status of elitist roleErifrom the global equilibrium points set Mbest,denoted as|RTMi〉.

Step 3Process the multilevel elitist roles’status by means of normalization to be|RTM1RTM2···RTMn〉.

Step 4Entangle the elitist roles’status through the quantum gateˆJ,and form the initial status as follows:

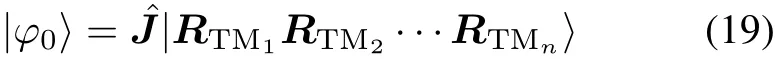
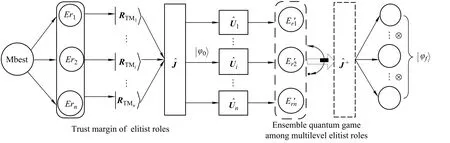
Fig.3 Ensemble quantum game flowchart of multilevel elitist roles

Step 5Assign the unitary operatorˆUito the strategy of corresponding elitist rolesErias follows:

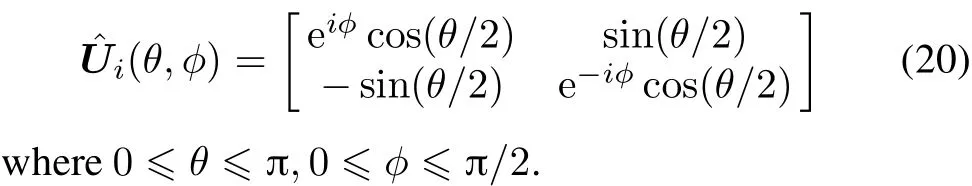
Step 6Update the status ofErito beafter quantum game among multilevel elitist roles.

Step 7Decode entanglement operator by using quantum gate,and combine multilevel elitist roleinto the ensemble status as follows:

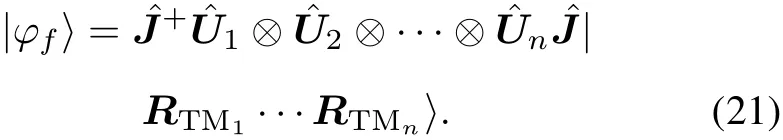
As the stated above,elitist rolesEriwill adjust the strategy according to the trust margin to find dynamics equilibrium points in relatively few iterations.The updated elitist rolecan share higher compensation payoff with neighborhood multilevel elitist roles.The main advantage of this method will provide an intriguing exhibiting structure to perfect the dynamics equilibrium of multilevel elitist roles for feature selection.

5.Proposed EERQG algorithm for feature selection

The proposed EERQG algorithm for feature selection includes three aspects:(i)Divide attribute sets and select optimal subpopulations;(ii)Construct the utility matrix of trust margins;and(iii)Implement ensemble quantum game for feature selection which will use the parallel manner of multilevel elitist roles to preserve elitists’diversity and to benefit from the various multilevel elitist roles.The structure diagram of EERQG is described in Fig.4.

The main steps are summarized as follows:

Algorithm 3EERQG

Step 1Generate evolutionary populationPopwith descending order and attribute setC.CodePopby using Q-bit presentation.DividePopintonsame subpopulationsSubpopi(i=1,2,...,n).

Step 2Map evolutionary subpopulations into equalarea regions(Pe1,Pe2,...,Pen)of multilevel elitist roles,and divideSubpopiin each pentagon into five equalarea triangles.

Step 3Assign the probability to each subpopulationSubpopiwhich is used to represent attribute subsetSubCi(i=1,2,...,n).The probability value is initialized as 1/n,namely,each subpopulationSubpopihas the equal selection probability to represent attribute subsetSubCi.

Step 4The probability will adaptively improve along with the evolution ofSubpopiin each pentagon as follows:

In the initial iteration,thejth attribute subset is assigned into theith quantumSubpopi.In the following(k+1)th iteration,the probability,of which theith quantumSubpopirepresents thejth attribute subsetSubCj,is defined as

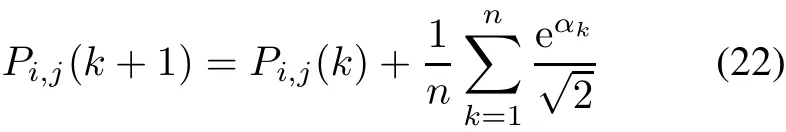
whereαkdenotes the learning rate of quantumSubpopi,andαk∈[0.5,1].

Step 5Compute the average represent probabilityPi,jas follows:

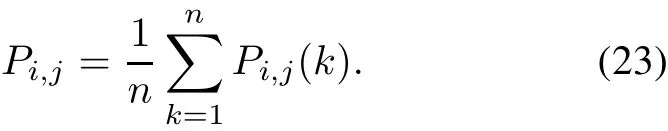
Step 6Construct the probability matrix of which subpopulations represent attribute subsets as follows:

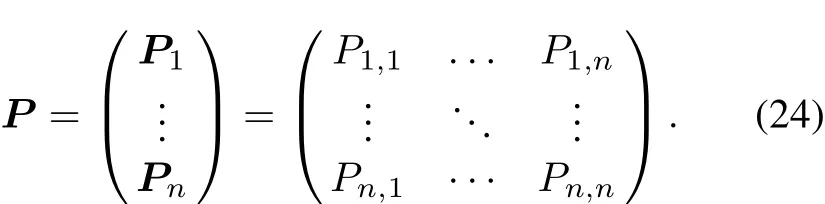
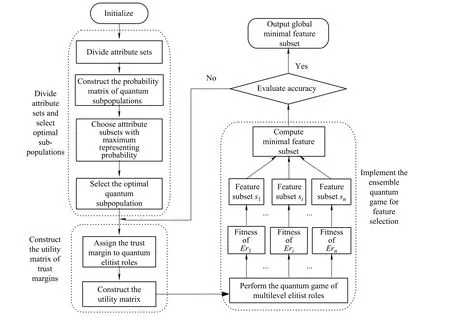
Fig.4 Structure diagram of EERQG

Step 7Compare different probability values where subpopulations represent thejth attribute subsetSubCjin the probability matrixP.

Step 8Select the optimalSubpopiwith the maximum probability value,and determineSubpopito evolveSubCj.

Step 9Conduct the multilevel elitist roles based dynamics equilibrium strategy by using Algorithm 1 to produce global equilibrium points set of multilevel elitist roles Mbest.

Step 10Compute each quantum elitist role’s fitnessFitness(x)in eachSubpopi,and select this quantumErias the optimizer ofSubpopi.

Step 11Construct the utility matrix of trust margins forEriin feature selection.

(i)Assign the trust margin to eachEriand set up the corresponding utility matrix of trust marginRTMiby using(17)and(18).

(ii)Form a stable equilibrium by the dynamic adjustment of elitist roles’trust margins.

Step 12Perform the ensemble quantum game of multilevel elitist roles by using Algorithm 2.

(i)Construct the quantum game strategy of elitist roles to execute the selection of feature subsets.

(ii)Perform the strategy ofErito be the best dynamics response for the game withErj,and then achieve the equilibrium of the quantum game byEri.

(iii)Adjust the strategy ofEriaccording to observed states so as to refine and update the stable equilibrium states.

(iv)Compute the fitness value ofEriFitness(Eri)so as to attain the attribute subsetSubCi.

(v)Compute the average optimal fitness values as follows:

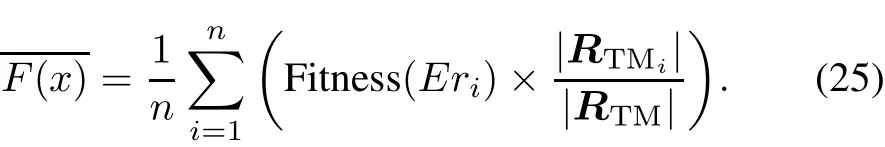
Step 13Compute minimal feature subset ofSubCi,namelyFea(Sub Ci)min,when the average optimal fitnessF(x)is obtained.The ensemble,which uses the parallel manner to benefit from the various multilevel elitist roles,can be applied to the combinations of feature subsets.Thus the global minimal feature set is achieved as follows:

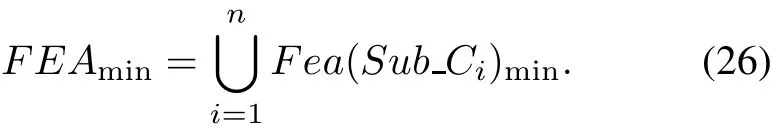
Step 14Evaluate whether the accuracy of feature selection is satisfied with the predefined value or not.

If Yes,output the global minimum feature selectionFEAmin;Else go to Step 10.

6.Experimental results and discussions

In order to determine the efficiency and effectiveness of EERQG,we conduct a series of experiments to evaluate its performance in terms of selected features,running time,and classification accuracy,comparing with several representative algorithms.The computer system is Windows XP(SP1)with Intel Pentium(R)4 4.00GHz CPU,4 GB RAM.Each algorithm is coded in Matlab 7.5 and the software is VS.NET 2013.Here we present the average result after 30 runs and the best mean value achieved is shown in Bold.

6.1 Feature selection experiment on UCI datasets

Ten UCI machine learning datasets[27]are selected to verify the performance of feature selection algorithms.To reveal this effect more clearly,we compare EERQG’s performance with some state-of-the-art feature selection algorithms,namely,the distance metric tolerance rough set algorithm(DM-TRS)[15]and the feature selection algorithm based on conditional entropy(FSCE)[17].The comparison results of three algorithms on ten UCI databases are given in Table 1,in which Time is the running time,Space is the space consumption and FSn is the number of selected features.

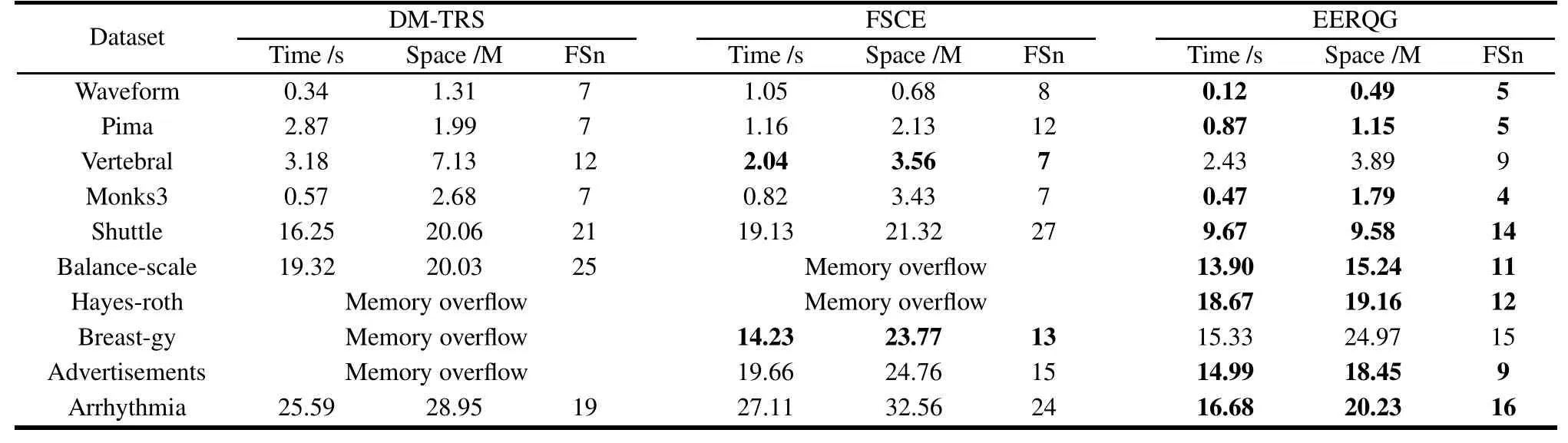
Table 1 Comparison of statistical feature selection performance for three algorithms on ten UCI datasets

As shown in Table 1,EERQG significantly outperforms DM-TRS and FSCE,and it is the best performer for eight of ten datasets.For the remaining two datasets,EERQG is only slightly inferior to FSCE.It is remarkable that in our implementation,the big space consumption leads to the memory overflow for DM-TRS in Hayes-roth,Breast-gy and Advertisements datasets,and for FSCE in Balance-scale and Hayes-roth datasets.The results show that EERQG can effectively select minimal feature subsets from UCI datasets with retaining the discerning ability of original features,meanwhile,EERQG would reduce the computational cost and small space consumption and guarantee the relatively higher accuracy of feature evaluation.

To study how the EERQG’s performance increases with the size of datasets increasing in this subsection,the Prima dataset is specially employed to implement the experimental comparison as an illustration.In Fig.5,thex-coordinate pertains to the size of the dataset,while they-coordinate gives the computational time and space consumption,respectively.It is easy to observe that both computational time and space consumption for the three algorithms increase with the increasing of the size of the dataset,nevertheless the computational time and space consumption achieved by EERQG are obviously less than DM-TRS and FSCE.The main reason should be attributed to the fact that EERQG can avoid the recalculations which facilitate the computation of new feature subsets by exploiting some previous results.So the computational efficiency is greatly improved and the space consumption is decreased.This result confirms EERQG is better than other feature selection algorithms.

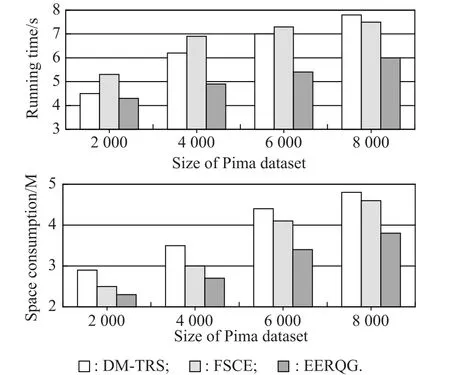
Fig.5 Comparison of feature selection algorithms on dynamic Pima dataset

6.2 Classification on UCI real datasets

In the following experiments,we evaluate the EERQG’s effectiveness in terms of classification accuracy and time.The above ten UCI data sets[27]are still employed to estimate the classification performance.We use 70%of the data as the training set and 30%of the data as the testing set,moreover,in the 70%,55%for training and 15%for validation.Thus,the redundant features from the current training set are deleted,and the rules from the training set are extracted.The testing set is well classified by using the rules generated from the training set.The results are shown in Table 2 and Table 3.

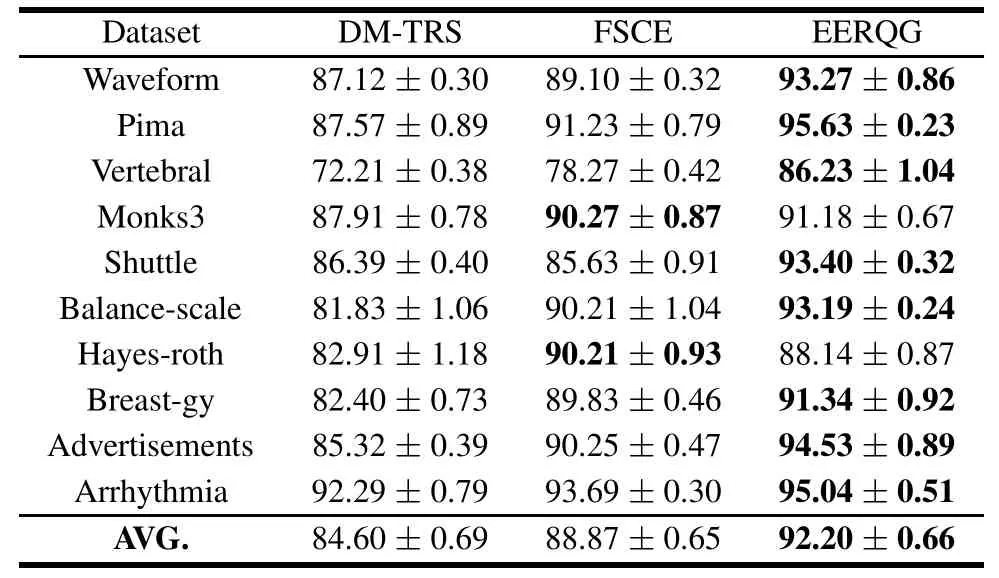
Table 2 Comparison of statistical classification accuracies for three algorithms on ten UCI datasets(Test±Standard/%)

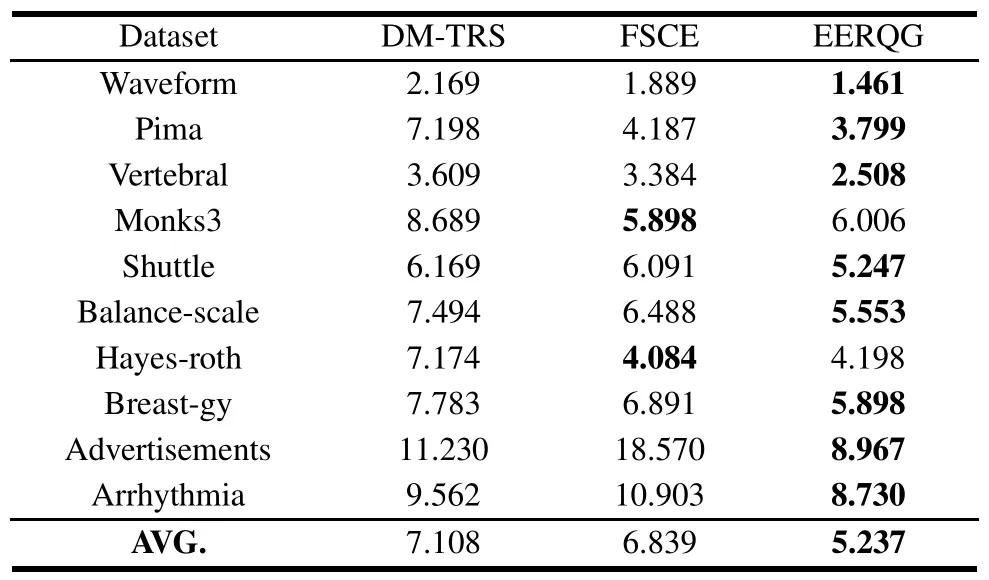
Table 3 Comparison of statistical classification time from three algorithms on ten UCI datasets s

We can draw some interesting conclusions as follows:

First of all,it is noticeable that EERQG achieves more excellent performance than DM-TRS and FSCE,except in Monks3 and Hayes-roth datasets.This suggests that EERQG has a strong classification ability,and it is an effective way to retain the most useful minimal feature subsets as few as possible.

Second,EERQG achieves higher classification accuracy than DM-TRS on all UCI datasets.Especially in the Balance scale,Breast-gy and Advertisements datasets,and the classification accuracy is obviously improved by 11.36%,8.94%and 9.21%,respectively,which is able to further confirm the strong competitiveness of EERQG.

Third,compared with FSCE,the classification accuracy of EERQG is better than or nearly equal to FSCE in most UCI datasets.It can be obviously improved in the eight datasets,and EERQG also has the nearly equal accuracy as FSCE in the remaining Monks3 and Hayes-roth datasets.It is indicated the overall classification performance of EERQG is superior to FSCE.

Moreover,the comparison of statistical classification time in Table 3 also justifies the better superiority of EERQG.All in all,we can conclude that EERQG achieves much better classification results than other state-of-the-art algorithms in terms of classification accuracy and time.

6.3 Robustness evaluation with noisy observation

In order to further test the robustness of EERQG,DM-TRS and FSCE algorithms on Shuttle and Breast-gy datasets with different percentages of noise,we randomly drawk%(k=5,10,15,20,25 and 30)the objects from original datasets and replace their decision labels with arbitrary candidates.These objects are considered to be the class noise and put back to to original datasets.With different percentages of noise,the variations curves of the average classification accuracy are shown in Fig.6,respectively.

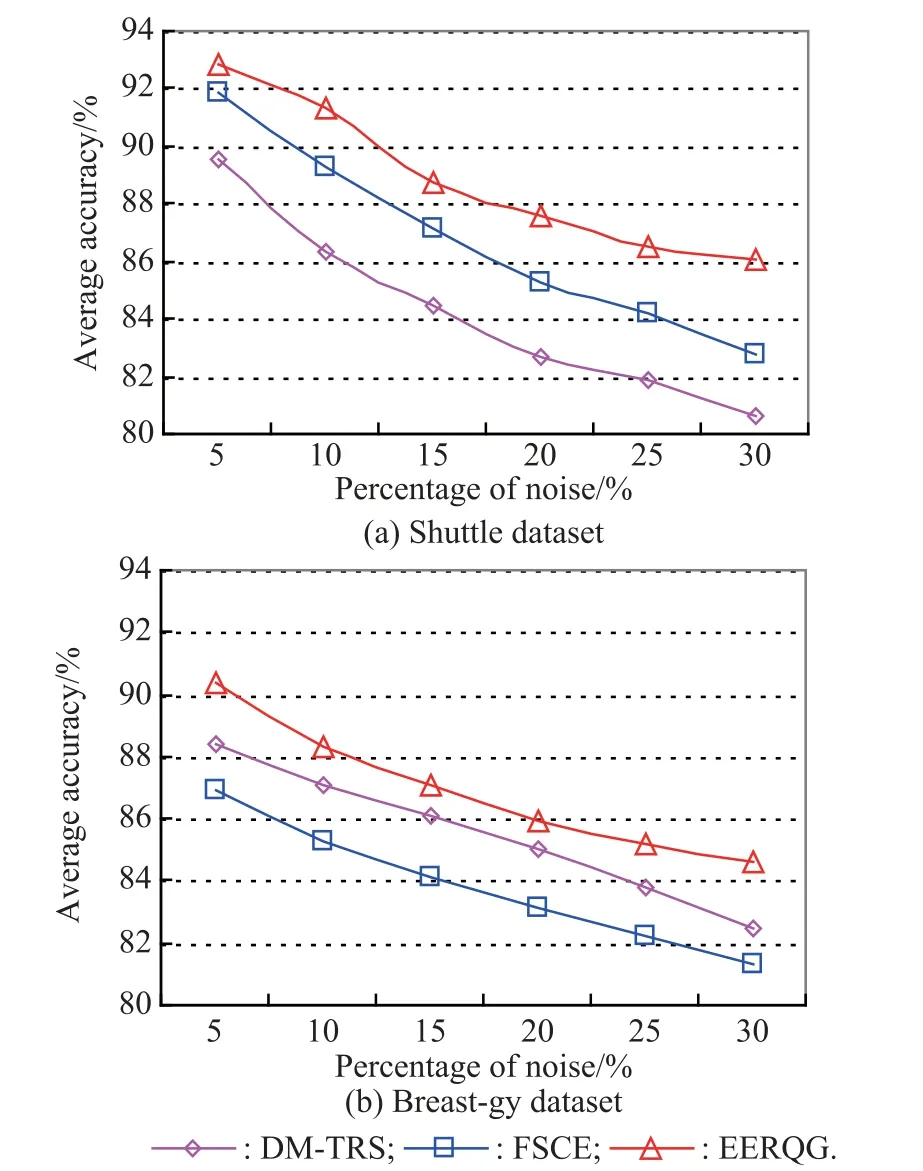
Fig.6 Comparison of classification accuracy on Shuttle and Breastgy datasets with different percentages of noise

As the percentage of noise increases,we can see the value variation of EERQG is smaller than those of DMTRS and FSCE.As shown in Fig.6(a),at the point of 30%in the Shuttle dataset,the classification accuracy value reaches 86.1%,80.6%and 82.8%for EERQG,DM-TRS and FSCE,respectively.Furthermore,the variations curve of EERQG finally trends to stabilization with the percentage of noise increasing,where the number of selected features is the least and the accuracy is the best,but the classification accuracies of DM-TRS and FSCE still decrease rapidly.The phenomenon may result from the reasons by utilizing the ensemble quantum game strategy of multilevel elitist roles,and the elitist roles’equilibrium points can attain the optimal profit results to achieve the win-win utility solutions,which can enhance the stable performance of feature selection and classification.The similar results in the Breast-gy dataset are also shown in Fig.6(b).The results further indicate EERQG is more robust to noise than the other two feature selection algorithms.

On ten UCI datasets,a series of comparison results validate that EERQG can provide the efficient feature selection and attain better stable solution in most datasets.Consequently,we can conclude that EERQG is a good alternative for feature selection and classification,and it is recommended to deal with the large-scale datasets in many real-world applications.

7.Conclusions

Feature selection is a challenging problem in areas of data mining,knowledge discovery,and machine learning.It has become increasingly essential for reducing the cost of computation and storage,and for improving the accuracy of model learning.In this paper,we present EERQG algorithm for feature selection.The multilevel elitist roles based dynamics equilibrium strategy is established,and the ensemble quantum game strategy is designed to perfect dynamics equilibrium of multilevel elitist roles during feature selection.Our experimental results show that the proposed EERQG algorithm is more effective and stable to utilize feature selection than some other representative algorithms.It provides a good way to handle the feature selection and classification problem in some large-scale realworld applications.

In our future work,we would further study the quantum co-evolutionary game mechanism and present some new methods for feature selection in the dynamic incomplete datasets,which is of more importance for real applications.

[1]A.K.Jain,D.Zongker.Feature selection:evaluation,application,a small sample performance.IEEE Trans.on Pattern Analysis and Machine Intelligence,1997,19(2):153–158.

[2]Z.Pawlak,A.Skowron.Rudiments of rough sets.Information Sciences,2007,177(1):3–27.

[3]Z.Pawlak,A.Skowron.Rough sets:some extensions.Infor-mation Sciences,2007,177(1):28–40.

[4]G.Y.Wang,Y.Y.Yao,H.Yu.A survey on rough set theory and its application.Chinese Journal of Computers,2009,32(7):1229–1246.(in Chinese)

[5]R.W.Swiniarski,A.Skowron.Rough set methods in feature selection and recognition.Pattern Recognition Letters,2003,24(6):833–849.

[6]R.Jensen,Q.Shen.Fuzzy-rough attribute reduction with application to web categorization.Fuzzy Sets and Systems,2004,141(3):469–485.

[7]P.Maji,P.Garai.On fuzzy-rough attribute selection:criteria of max-dependency,max-relevance,min-redundancy,and maxsignificance.Applied Soft Computing,2013,13(9):3968–3980.

[8]J.M.Smith.Evolution and the theory of games.New York:Cambridge University Press,1982.

[9]J.Eisert,M.Wilkens,M.Lewensein.Quantum game and quantum strategies.Physical Review Letters,1999,83(15):3077–3080.

[10]D.Meyer.Quantum strategies.Physical Review Letters,1999,82(5):1052–1055.

[11]M.Sun,D.W.Lu,C.Y.Ju,et al.An applicable multipleplayer’s quantum market game.Journal of University of Science and Technology of China,2012,42(4):259–264.(in Chinese)

[12]E.Ahmed,M.F.Elettreby,A.S.Hegazi.On quantum team games.International Journal of Theoretical Physics,2006,45(5):907–913.

[13]M.Yang,P.Yang.A novel condensing tree structure for rough set feature selection.Neurocomputing,2008,71(4/6):1092–1100.

[14]M.Yang,P.Yang.A novel approach to improvingC-Treefor feature selection.Applied Soft Computing,2011,11(2):1924–1931.

[15]N.M.Parthal´ain,Q.Shen.Exploring the boundary region of tolerance rough sets for feature selection.Pattern Recognition,2009,42(5):655–667.

[16]Y.H.Qian,J.Y.Liang,W.Pedrycz,et al.An efficient accelerator for attribute reduction from incomplete data in rough set framework.Pattern Recognition,2011,44(8):1658–1670.

[17]L.Sun,J.C.Xu,Y.Tian.Feature selection using rough entropy-based uncertainty measures in incomplete decision systems.Knowledge-Based Systems,2012,36:206–216.

[18]W.P.Ding,J.D.Wang,Z.J.Guan,et al.Enhanced minimum attribute reduction based on quantum-inspired shuffled frog leaping algorithm.Journal of Systems Engineering and Electronics,2013,24(3):426–434.

[19]W.P.Ding,J.D.Wang,Z.J.Guan.A novel minimum attribute reduction algorithm based on hierarchical elitist role model combining competitive and cooperative co-evolution.Chinese Journal of Electronics,2013,22(4):677–682.

[20]X.A.Ma,G.Y.Wang,H.Yu.Heuristic method to attribute reduction for decision region distribution preservation.Journal of Software,2014,25(8):1761–1780.(in Chinese)

[21]J.Qian,D.Q.Miao,Z.H.Zhang,et al.Parallel attribute reduction algorithms using MapReduce.Information Sciences,2014,279:671–690.

[22]J.P.Herbert,J.T.Yao.Game-theoretic rough sets.Fundamenta Informaticae,2011,108(3/4):267–286.

[23]X.Sun,Y.H.Liu,J.Li,et al.Feature evaluation and selection with cooperative game theory.Pattern Recognition,2012,45(8):2992–3002.

[24]N.Azam,J.T.Yao.Analyzing uncertainties of probabilistic rough set regions with game-theoretic rough sets.Interna-tional Journal of Approximate Reasoning,2014,55(1):142–155.

[25]G.X.Zhang.Quantum-inspired evolutionary algorithms:a survey and empirical study.Journal of Heuristics,2011,17(3):303–335.

[26]J.Q.Gao,J.Wang.A hybrid quantum-inspired immune algorithm for multiobjective optimization.Applied Mathematics and Computation,2011,217(9):4754–4770.

[27]A.Asuncion,D.J.Newman.UCI repository of machine learning databases.http://www.ics.uci.edu/～mlearn/mlrepository.htm.