Quantifying cardinal temperatures and thermal time required for germination of Silybum marianum seed

Ghsem Prmoon，Seyed Amir Moosvi*，Hmed AkriAli Edi

aDepartment of Agronomy and Plant Breeding，Faculty of Agriculture，Mohaghegh Ardabili University，Ardabil，Iran

bDepartment of Agronomy，Faculty of Agriculture，Tarbiat Modares University，Tehran，Iran

Quantifying cardinal temperatures and thermal time required for germination of Silybum marianum seed

Ghasem Parmoona，Seyed Amir Moosavib，*，Hamed Akbarib，Ali Ebadia

aDepartment of Agronomy and Plant Breeding，Faculty of Agriculture，Mohaghegh Ardabili University，Ardabil，Iran

bDepartment of Agronomy，Faculty of Agriculture，Tarbiat Modares University，Tehran，Iran

A R T I C L E I N F O

Article history：

25 October 2014

Accepted 13 November 2014

Available online 12 January 2015

Silymarin

Regression models

Cardinal temperatures

Seed germination

The response of seed germination to environmental factors can be estimated by nonlinear regression.The present study was performed to compare four nonlinear regression models（segmented，beta，beta modified，and dent-like）to describe the germination rate-temperature relationships of milk thistle（Silybum marianum L.）at six constant temperatures，with the aim of identifyingthecardinaltemperaturesandthermaltimesrequiredtoreachdifferentgermination percentiles.Models and statistical indices were calibrated using an iterative optimization method and their performance was compared by root mean square error（RMSE），coefficient of determination（R2）andAkaikeinformationcriterioncorrection（AICc）.Thebetamodelwasfound to be the best model for predicting the required time to reach 50%germination（D50），（R2=0.99；RMSE=0.004；AICc=-276.97）.Based on the model outputs，the base，optimum，and maximum temperatures of seed germination were 5.19±0.79，24.01±0.11，and 34.32±0.36°C，respectively.The thermal times required for 50%and 90%germination were 4.99 and 7.38 degree-days，respectively.

©2015 Crop Science Society of China and Institute of Crop Science，CAAS.Production and

hosting by Elsevier B.V.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

1.Introduction

Herbal medicine is an alternative approach to conventional medical therapies.Medicinal plants may incur smaller side effects than chemical drugs.Silybum marianum is a broadleaf plant with highly valued medicinal properties.Its seeds contain flavonolignans，silybin，silychristin，and silydianin，together called silymarin［1］.Silymarin is used in liver disease therapy［2］.

Successful production of medicinal plants requires a strong knowledge of plant ecophysiology.Most medical plants have unknown ecophysiology，owing to their existence in harsh and wild habitats.Vigorous seed germination and seedling establishment are highly desirable，especially in arid and semiarid climates.Studying basic seed germination requirements will increase the chance of successful plant establishment under different climatic conditions［3］.Upon receiving special cues from the environment，seeds initiate germination.In some circumstances，plants spread the risk of early germination for their seeds or apply alternative mechanisms to maximize fitness for germination［4，5］.The seed environment consists of soil temperature，moisture，gases，light，andchemical substances，also considered to be abiotic germination regulators［6，7］.Among all effective factors of seed germination，temperature and moisture are considered the most important.

Usually，a linear increase in germination rate is associated with an increase in temperature from base temperature（Tb）to an optimum.An increase of temperature from the optimum will reduce the germination rate to zero［8-12］.To determine the best planting date for plants，it is necessary to find the base（Tb），optimum（To）and maximum temperatures（Tc）for seed germination.These are known as cardinal temperatures［6］.Although there is a rich body of data describing the cardinal temperatures for many agronomic crops and plant species，information about the thermal requirements of many weedy and medicinal plants is lacking.Modeling of seed germination is considered an effective approach to determining cardinal temperatures for most plant species，although these methods have some limitations due to unpredictable biological changes.Two main concepts widely used by researchers to model seed germination include empirical and mechanical models［13］.Empirical models perform well for fitting individual germination data over time，but may need empirical variables［14］.It is difficult to ascribe biological significance to model parameters estimated by empirical methods［9，13］.Mechanical models are developed based on the experimental quantification of environmental effects on seed germination and seedling emergence.In the long term，this approach is likely to be most successful［9，15］.The application of mechanical threshold models of seed germination and seedling emergence has shown some success［11，12，15-18］.The results of fitting mechanical models are usefulforevaluatingseedquality，germinationrate，germination percentage，germination uniformity［13，19］and seed performance under different environmental stresses such as salinity，drought，and freezing［11］.Regression models incorporating more parameters can produce more precise estimates.Nonlinear curves are used to model the time course of germination at different temperatures［20］.Such regression models have been used to explain development rate in many crops［21］.Seedling emergence of wheat as a function of soil temperature and water potentialhasbeenstudiedusinglogisticmodels［22-24］Cardinal temperature was determined using segmented and logistic models in millet varieties and seedling emergence of wheat［25-27］.Inthedent-likemodelatlower-than-optimum temperature，a linear relationship holds between temperature and germination rate.This relationship remains linear at higher-than-optimumtemperatures，butwithareducing trend.With increasing temperature，germination rate increases linearlyup to anoptimumtemperature.Beta and beta modified models fit curvilinear relationships between germination rate and temperature.These models are thus more flexible than other models.

This study was performed to determine the effectiveness of nonlinear regression models including dent-like，segmented，beta，andbeta modified for cardinaltemperaturesestimation of Silybum marianum seeds.The results of this study will be useful for characterizing the ecophysiology of seed germination of milk thistle seeds.Such knowledge may be useful for identifying the best planting dates for this medicinal plant in a range of climates and regions.

2.Material and methods

An experiment was performed to determine the cardinal temperatures of S.marianum.Seeds of S.marinum were purchased from the Pakanbazr Co.，Iran.The experiment was conducted using germinators with controlled environments in the Seed Technology Laboratory，Faculty of Agriculture，Mohaghegh Ardabili University，Ardabil，Iran.Four replicates of 50 seeds were germinated in 9-cm-diameter Petri dishes on two layers of Whatman No.1（9 cm diameter）filter paper containing 5 mL distilled water.The germination responses were evaluated at six constant temperatures:10，15，20，25，30，and 35°C.

Seedswithradicleselongatedatleast2 mmwereconsidered as germinated.Germinated seeds were counted every 24 h and cumulative germination percentage was plotted against time. From this curve，the time required to reach 50%germination（D50）was determined by fitting a logistic model of cumulative germination percentage（G）against time（t）as described by Eq.（1）:

whereGxisthe maximumgermination percentage，t isthe time required for 50%germination，and a and b are constants.The times for 10%，50%，and 90%germination were also determined by interpolation and are designated as D10，D50，and D90，respectively［20，28，29］.

The reciprocal of the time taken for a given fraction of the seed population to germinate was considered to be the germination rate（GR）.

To quantify the response of the germination rate to temperature and cardinal temperatures for germination，the following equation was used:

where f（T）is a T function（reduction factor）that ranges between 0 at the base and maximum temperatures and 1 at the optimal temperature（s），and 1/fois the inherent maximum rate of germination at the optimal temperature，estimated by an iterativeoptimizationmethod.Thus，forepresentstheminimum number of hours for germination at the optimal temperature［30］.The GR also shows the germination rate of a given percentile.Sigma Plot，Ver 12 software was used to calibrate themodels（beta，betamodified，segmented，anddent-like）using an iterative optimization method（Table 1）.To determine the best estimates of the parameters（lower deviations of the interceptfrom 0 and of the slope from 1 correspond to increased reliability（RMSE；Eq.（3）），the coefficient of determination（R2；Eq.（4）），andtheinterceptandslopeoftheregressionofpredicted vs.observed germination rate were used.

Table 1-Beta，segmented，and dent-like models that were fitted to model germination rate at different constant temperatures.

where Yobsdenotes observed value，Ypredpredicted value，and n the number of samples［31］，and

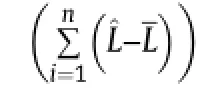
Low RMSE and R2near 1 correspond to better model estimation.

To identify the best model for estimating cardinal temperature，the Akaike Information Criterion（AIC）was used. This statistic incorporates the amount of reduction of RSS and the model complexity［32］.

where RSS denotes the residual sum of squares，n the number of observations，and k is the number of model parameters.

It is possible to use a corrected AIC（AICc）instead of AIC. This statistic is used to identify the most accurate model［33，34］.

The model that yields the most accurate estimate is the one with the lowest AICc value.Although the best model is the one that yields the lowest AICc，there is a method that permits description，ranking，and fitting different models. This method requires the calculation of Δi:

where min AICc is the minimum calculated AICc among all models，and corresponds to the best-fitting model.If Δi＜10，there is no significant difference between models，and a model with higher AICc also could be well-fitting.If Δi＞10，a model with higher AICc is not suitable and not well-fitting.

The daily thermal time（DTT）was calculated as DTT=（To-Tb）.f（T）where:

f（T）is the T function，To1is the lower optimum T，and Tbis the base T.The first components of daily thermal time are the constant and non-optimal temperatures that affect the daily thermal time through f（T）.

3.Results

In this study，AICc was our main criterion for choosing the best experimental models by which to evaluate cardinal temperatures.The calculated AICc values for the segmented model were -198.78，-248.53，and-237.07forD10，D50，andD90，respectively. The AICc indices for the beta model outputwere-247.11，276.97，and-258.98forD10，D50，andD90，respectively，andthoseforthe output of beta modified were-217.17，262.02，and-252.28 for D10，D50，and D90，respectively（Table2）.The calculated AICc for the dent-like model in D10，D50，and D90 were-205.63，-264.94，and-257.72，respectively.Modelsofrelativegerminationratevs. mean temperature were fitted（Fig.1），and their parameter estimates are presented in Table 1.Tbwas estimated for D10，D50，and D90 using segmented（8.32±0.47，7.49±0.32，6.98± 0.66），beta（4.47±0.39，5.19±0.79，6.05±0.11），beta modified（7.49±1.27，5.79±0.79，3.94±1.79），and dent-like（8.32±0.44，7.49±0.23，6.98±0.43）.The base and maximum temperatures for differentpercentiles showed no significantdifference for any of the tested models.According to the beta model for D10 and D50，the optimum temperature varied between 24.12±0.14 and 24.01±0.11.Thismodel was mostreliable for D10，D50，and D90，because of the higher determination coefficient between observed and predicted values（R2values of 0.99，0.99，and 0.96 for the pooled data）.The beta-modified and segmented modelsalso appeared reliable for D10 and D550（Table 2），with high calculated R2values for both models.

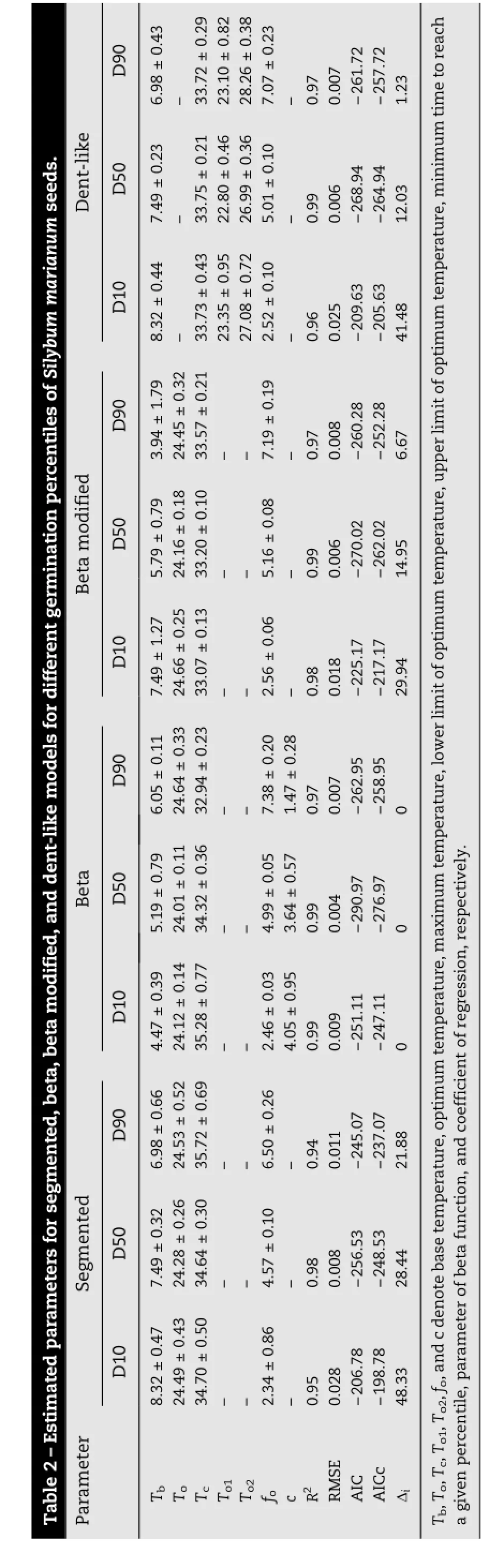
According to the output of the segmented model，the optimum temperature varied between 24.28°C and 24.50°C in D10 to D90.The output of the dent-like model was not reliable for predicting D10，D50，and D90，as evident from the low determination coefficients（R2values of 0.96，0.99，and 0.97，respectively）.The segmented model estimated the base，optimum，and maximum temperatures for D50 as 7.49±0.32，24.28±0.26，and 34.64±0.30，respectively.The beta modified model estimated the base，optimum，and maximum temperatures for D50 as 5.79±0.79，24.16±0.18，and 33.20±0.10，respectively.The optimum temperature for all models was very close to 24°C.The beta model yielded the best-fitting output for cardinal temperatures，as shown by its higher R2for D10，D50，and D90:0.99，0.99，and 0.97，respectively（Table 2）.In addition，the beta model yielded the lowest RMSE values for D10，D50，and D90（0.009，0.004，and 0.007）among all models（Table 2）.

The optimum temperature of D50 was estimated by the segmented，beta，and beta modified models as 24.28±0.26；24.01±0.11，and 24.16±0.18，respectively，whereas for the dent-like model the optimum temperature for D50 ranged from 22.80±0.46（To1）to 26.99±0.36（To2）.The calculated cardinal temperatures using the beta and beta modified models both exhibited a sigmoidal shape（Fig.1a and b）.The graphical output of the segmented model is illustrated in part C of Fig.1.The dent-like model could not estimate an exact optimum temperature and instead yielded a temperature range（Fig.1d）.Thecalculatedf（T）fortheconstanttemperatures used in this study，based on the beta model，is illustrated in Fig.2.It shows an increasing trend up to 25°C，after which it starts to decrease.This observation suggests that the optimum temperature is around 25°C.The calculated thermal times for each germination percentile based on the pooled data are shown in Fig.3.

Our results confirmed the accuracy of estimated parameters and the reliability of the beta model.

4.Discussion

Thermal time（degree days or hours）is the basic and most important temperature factor in plant growth and development processes［35］such as seed germination and seedling emergence［36］.Thermal time is widely used to quantify and model seed germination.Temperature plays a critical role in the regulation of plant vital processes，including seed germination［37］.Practical research in plant science usually attempts to establish the minimum temperature required for germination or its maximum range［38］.Seed germination of spring poppy varieties occurs at temperatures above 2-3°C，but the optimum temperature is 7-10°C.In contrast，the optimumgerminationtemperatureofwinterpoppyis 15-20°C［39］.

Our study suggested that a bilinear-shaped response model of germination rate to temperature is applicable for determination of the cardinal temperatures of S.marianum. In this model，germination rate is regressed separately on temperature for two extremes of temperature（below and above the optimum temperature）.Base（Tb）and maximumtemperatures（Tc）are the intercepts of each regression line［40，41］.The thermal times required to reach specified germination percentiles（D10，D50，and D90）were calculated from the reciprocal of the slope of the regression equation of rate of germination vs.temperature below the optimum［42］.

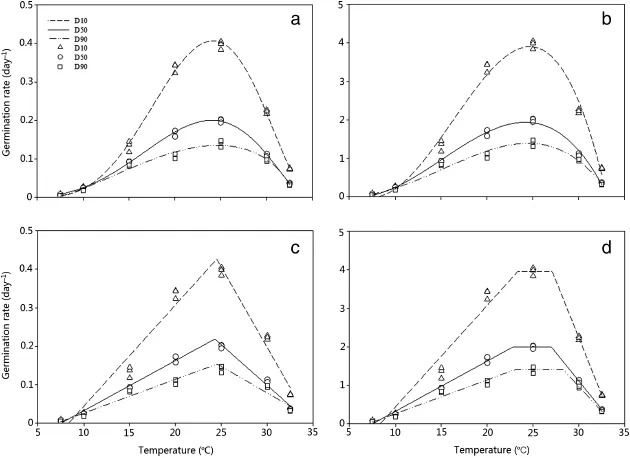
Fig.1-Predicted（lines）vs.observed（symbols）germination rate of Silybum marianum seeds at different constant temperatures for different germination percentiles（D10，D50，and D90）using beta（a），beta modified（b），segmented（c），and dent-like（d）models.

The results of the present study confirmed that，in the absence of other limiting factors（such as light and water），the germination of S.marianum seed was highly influenced by temperature.In addition，our results indicated that the beta model of germination rate sharply defines the cardinal temperatures of S.marianum.

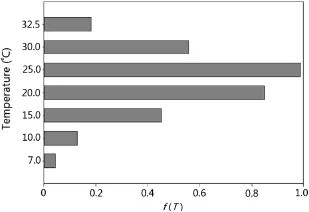
Fig.2-f（T）values for different constant temperatures based on the beta model.

R E F E R E N C E S

［1］P.Morazzoni，E.Bombardelli，Silybum marianum（Carduus marianus），Fitoterapia 66（1995）3-42.

［2］F.Rainone，Milk thistle，Am.Fam.Physician 72（2005）1285-1292.

［3］D.E.Goldberg，R.Turkington，L.Olsvig-Whittaker，A.R.Dyer，Density dependence in an annual plant community:variation among life history stages，Ecol.Monogr.71（2001）423-446.

［4］D.Cohen，Optimizing reproduction in a randomly varying environment，J.Theor.Biol.12（1966）119-129.

［5］T.Philippi，J.Seger，Hedging one's evolutionary bets，revisited，Trends Ecol.Evol.4（1989）41-44.

［6］J.D.Bewley，M.Black，Seeds:physiology of development and germination，Plenum Press，New York，1994.

［7］C.C.Baskin，J.M.Baskin，Seeds:ecology，biogeography，and evolution of dormancy and germination，Academic Press，San Diego，2001.

［8］J.Garcia-Huidobro，J.L.Monteith，G.R.Squire，Time，temperature and germination of pearl millet（Pennisetum typhoides S.&H.）:I. Constant temperature，J.Exp.Bot.33（1982）288-296.

［9］K.J.Bradford，A water relations analysis of seed germination rates，Plant Physiol.94（1990）840-849.

［10］K.J.Bradford，Water relations in seed germination，Seed Dev. Germination 1（1995）351-396.

［11］K.J.Bradford，Applicationsofhydrothermal timetoquantifying and modeling seed germination and dormancy，Weed Sci.50（2002）248-260.

［12］H.R.Rowse，W.E.Finch-Savage，Hydrothermal threshold models can describe the germination response of carrot（Daucus carota）and onion（Allium cepa）seed populations across both sub-and supra-optimal temperatures，New Phytol.158（2003）101-108.

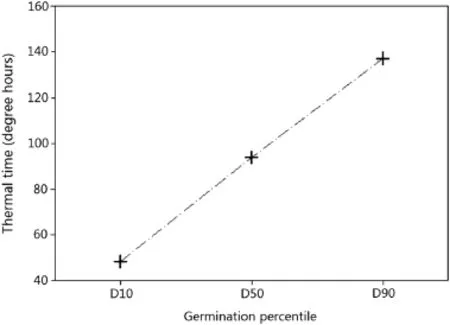
Fig.3-Thermal time（degree hours）required for different germination percentiles，based on pooled data，when T=To.

［13］R.Wang，Modeling seed germination and seedling emergence in Winterfat（Krascheninnikovia lanata（Pursh）A.D.J.Meeuse& Smit）:physiological mechanisms and ecological relevance，University of Saskatchewan，2005.

［14］R.F.Brown，D.G.Mayer，Representing cumulative germination: 2.The use of the Weibull function and other empirically derived curves，Ann.Bot.61（1988）127-138.

［15］F.Forcella，R.L.Benech Arnold，R.Sanchez，C.M.Ghersa，Modeling seedling emergence，Field Crops Res.67（2000）123-139.

［16］R.L.Benech Arnold，R.A.SaÂnchez，Modeling weed seed germination，in:J.Kigel，G.Galili（Eds.），Seed Development and Germination，Marcel Dekker，New York，1994，pp.545-566.

［17］P.S.Allen，S.E.Meyer，M.A.Khan，Hydrothermal time as a tool in comparative germination studies，in:M.J.Black，K.J. Bradford，J.Vázquez-Ramos（Eds.），Seed Biology:Advances and Applications，CABI Publishing，New York，2000，pp.401-410.

［18］E.S.Roman，S.D.Murphy，C.J.Swanton，Simulation of Chenopodium album seedling emergence，Weed Sci.48（2000）217-224.

［19］V.Alvarado，K.J.Bradford，A hydrothermal time model explains the cardinal temperatures for seed germination，Plant Cell Environ.25（2002）1061-1069.

［20］B.Shafii，W.J.Price，Estimation of cardinal temperatures in germination data analysis，J.Agric.Biol.Environ.Stat.6（2001）356-366.

［21］B.Kamkar，M.Jami Al-Alahmadi，A.Mahdavi-Damghani，F.J. Villalobos，Quantification of the cardinal temperatures and thermal time requirement of opium poppy（Papaver somniferum L.）seeds to germinate using non-linear regression models，Ind.Crops Prod.35（2012）192-198.

［22］R.E.Blackshaw，Soil temperature and moisture effects on downy brome vs.winter canola，wheat and rye emergence，Crop Sci.31（1991）1034-1040.

［23］I.S.I.Thomson，B.Kamkar，A.Koocheki，M.Nassiri Mahallati，P.Rezvani Moghaddam，Asian J.Plant Sci.5（2006）316-319.

［24］B.Kamkar，M.Ahmadi，A.Soltani，E.Zeinali，Evaluating non-linear regression models to describe response of wheat emergence rate to temperature，Seed Sci.Biotechnol.2（2008）53-57.

［25］M.Stapper，J.M.Lilley，Evaluation of simtag and wheat in simulating wheat phenology in Southeastern Australia，Proceedings of the 10th Australian Agronomy Conference，Hobart，2001 Available at http://www.regional.org.au/au/asa/ 2001/1/d/stapper.htm（accessed August 2012）.

［26］X.Yin，M.J.Kropff，P.K.Aggarwal，S.Peng，T.Hone，Optimal preflowering phenology of irrigated rice for high yield potential in three Asian environments:a simulation study，Field Crops Res.51（1997）19-27.

［27］J.F.Angus，D.H.Mackenzie，R.Morton，C.A.Schafer，Phasic development in field crops:II.Thermal and photoperiodic responses of spring wheat，Field Crops Res.4（1981）269-283.

［28］B.Marshall，G.R.Squire，Non-linearity in rate-temperature relations of germination in oilseed rape，J.Exp.Bot.47（1996）1369-1375.

［29］A.Soltani，Application of SAS in statistical analysis，JDM Press，Mashahd，2007.

［30］A.Soltani，M.J.Robertson，B.Torabi，M.Yousefi-Daz，R. Sarparast，Modelling seedling emergence in chickpea as influenced by temperature and sowing depth，Agric.For. Meteorol.138（2006）156-167.

［31］B.G.H.Timmermans，J.Vos，J.Van Nieuwburg，T.J.Stomph，P.E.L.Van der Putten，Germination rates of Solanum sisymbriifolium:temperature response models，effects of temperature fluctuations and soil water potential，Seed Sci. Res.17（2007）221.

［32］K.P.Burnham，D.R.Anderson，Model selection and multimodel inference:a practical information-theoretic approach，Springer-Verlag，New York，2002.

［33］M.A.Butler，A.A.King，Phylogenetic comparative analysis:a modeling approach for adaptive evolution，Am.Nat.164（2004）683-695.

［34］J.M.O'Meara，S.Burles，J.X.Prochaska，G.E.Prochter，R.A. Bernstein，K.M.Burgess，Thedeuterium-to-hydrogenabundance ratiotowardtheQSOSDSSJ155810.16-003120.0，Astrophys.J.649（2006）61-65.

［35］K.E.Fry，Heat-unit calculations in cotton crop and insect models，United States Department of Agriculture，Oakland，California，1983..

［36］R.H.Ellis，S.Covell，E.H.Roberts，R.J.Summerfield，The influence of temperature on seed germination rate in grain legumes:II.Intraspecific variation in chickpea（Cicer arietinum L.）at constant temperatures，J.Exp.Bot.37（1986）1503-1515.

［37］C.E.Bare，V.K.Tooke，W.A.Gentner，Temperature and light effects on germination of Papaver bracteatum，P.orientale and P.somniferum L.Planta Med.34（1978）135-143.

［38］D.Földesi，Papaver somniferum，in:J.Bernáth（Ed.），Vadontermô és Termesztett Gyógynövények，Mezôgazda Kiadó，Budapest，1994，pp.390-399.

［39］J.B.J.Dobos，Eltérõ származásu és vegetációs ciklusu Papaver somniferum fajták csirázásbiológiai vizsgálaza，Herba Hung 24（1985）35-48.

［40］S.Covell，R.H.Ellis，E.H.Roberts，R.J.Summerfield，The influence of temperature on seed germination rate in grain legumes:I.A comparison of chickpea，lentil，soyabean and cowpea at constant temperatures，J.Exp.Bot.37（1986）705-715.

［41］S.S.Phartyal，R.C.Thapliyal，J.S.Nayal，M.M.S.Rawat，G.Joshi，The influences of temperatures on seed germination rate in Himalayan elm（Ulmus wallichiana），Seed Sci.Technol.31（2003）83-93.

［42］J.H.M.Thornley，Modelling flower initiation，in:J.G.Athert（Ed.），Manip.Flowering，Butherworths，London，1987，p.6.

28 April 2014

in revised form

.

E-mail address:Amir.msa@gmail.com（S.A.Moosavi）.

Peer review under responsibility of Crop Science Society of China and Institute of Crop Science，CAAS.

http://dx.doi.org/10.1016/j.cj.2014.11.003

2214-5141/©2015 Crop Science Society of China and Institute of Crop Science，CAAS.Production and hosting by Elsevier B.V.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.