几何画板与数学课程整合的实例探究

张 宁

（贵州师范大学 贵州贵阳 550000）

几何画板与数学课程整合的实例探究

张 宁

（贵州师范大学 贵州贵阳 550000）

随着科学技术的发展，以计算机和网络技术为核心的现代教育手段如多媒体教学课件进入数学教育，使我们的教育模式产生质的飞跃。其中几何画板作为一个专门的数学教学软件，对传统的教学中由于教学工具的限制而无法清晰表述而产生的问题得以很好的解决。本文通过对两个教学实例的探究对这一点进行论证。

几何画板 数学教学 三角函数

一、问题提出

传统的教学模式是“粉笔+黑板+教材”，这种教学模式是静态的，离散的，对于一些连续变化，动态的内容，教师只能在用在黑板上通过不断的描述，绘画才能讲解，这样的教学方法产生的教学效果往往是教师讲的口干舌燥，学生听的云里雾里。长此以往自然就让学生觉得数学很难，只有聪明的人才能学懂数学。

尤其是高中数学以其高度的抽象性和严密的逻辑性成为大多数高中生学习中难以掌握的一门学科，这就要求教师能够具体清晰的讲解知识，让学生有一个更加直观的认识也尤为重要。而几何画板就是可以达到这样的教学效果。以下我从对正弦函数图像两种教学的对比中具体阐述。

二、正弦函数图像教学对比

正弦函数的图像在教学过程中如果要讲解清楚为什么描点后要用圆滑的曲线连接太过于复杂，而且没有必要花太多的时间在这类问题上，所以一般教师在讲到这个问题时，要就一带而过，要么就忽略不提，但是这类型的处理有使学生产生疑惑，当学生产生疑惑而得不到解决时就会极大的影响学生学习的积极性，而使用几何画板就可以很好的解决此类问题。

1.传统的教学

在传统的教学中教师一般采用五点法来设计这部分内容具体操作如下：

（1）给出一个单位圆

（2）让学生绘制这样的一个表格

α 0 2ππ2sin010-103ππ2 α

（3）在直角坐标中找出对应的点，然后用圆滑的曲线连接得；

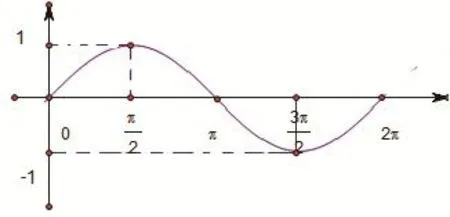
但是学生会产生这样的疑惑，为什么图像不可以是这样的，

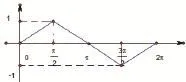
2.利用几何画板教学

我们可以参照《几何画板5.X课件制作实用教程》［1］第112页，即可做出如下图形，根据终边相同的同名三角函数值相等，把上述图象沿着x轴向右和向左连续地平行移动，每次移动的距离为2π，就得到y=sinx，x∈R的图象.

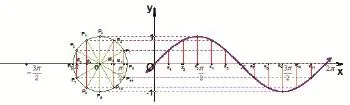
把角x（）xR∈的正弦线平行移动，使得正弦线的起点与x轴上相应的点x重合，则正弦线的终点的轨迹就是正弦函数y=sinx的图象.

显然，在计算机上进行这样的演示，不仅节约时间而且可以使学生更加直观的认识正弦函数图形的形成过程。

3.反思

其实在高中数学教学中有很多类似的问题如：

（1）离心率的范围与圆锥曲线得关系，学生不明白为什么椭圆的离心率大于0而小于1，双曲线是大于1的而抛物线就为1。

（2）动点的轨迹方程，学生只靠想象是很难完成的。

（3）立体几何中的截面问题，一个正方体为什么会被一个平面截出一个五边形等问题。

这类问题都成为了学生学习中难以理解而教师由于教学工具的限制不能讲解清楚的题目，这样就使简单的问题复杂化了但是如果能合理的利用几何画板在教学中可达到事半功倍的效果。

三、总结

几何画板通过对点、线、面基本元素进行变换、构造、测量和计算、跟踪轨迹等操作，从而构造出其他较为复杂的图形，使静态的图形变动态，抽象的概念变形象，枯燥的内容变有趣，可以准确的表达数学概念［2］。可应用在在平面几何、数与代数、立体几何、解析几何等方面。［3］特别是可以突破传统教学中定的所有几何图形基本性质都保持不变的难点，几何花瓣的有效利用可以更好地揭示知识之间的内在联系，学生可以更好地理解知识的发生和发展的过程。

［1］缪亮，盘俊春.《几何画板5.X课件制作实用教程》［M］.清华大学出版社，2012.

［2］赵国义.用几何画板教学的体会［J］.数学通报，2002，（11）.

［3］陈福宝.《几何画板》促进数学学习的实践研究［D］.南京：南京师范大学，2008.