茶苏打饼干货架寿命预测模型的建立

李新旺， 张 晶， 李雪影， 徐 辉， 陆 宁

（安徽农业大学茶与食品科技学院，安徽合肥 230036）

茶苏打饼干货架寿命预测模型的建立

李新旺， 张 晶， 李雪影， 徐 辉， 陆 宁*

（安徽农业大学茶与食品科技学院，安徽合肥 230036）

采用两种数学模型，即Arrhenius模型和Q10模型，预测茶苏打饼干的货架期并比较误差值，确定最优模型。以一级动力学理论为基础，研究了不同温度（24，34，44，54℃）储藏过程中，茶苏打饼干的过氧化值随时间的变化，利用Arrhenius方程和Q10方程建立储藏温度和过氧化值反应速率的关系，验证茶苏打饼干在28，38，48℃条件下的货架期并与真实值对比。结果表明Arrhenius模型的最大预测误差达到10.9%，Q10模型的最大预测误差为4.3%。因此，Q10模型可以较好地反应货架寿命和温度之间的关系。相比于Arrhenius模型，Q10模型的准确性更高，可以用来预测茶苏打饼干的货架期。

动力学模型；过氧化值；货架期

苏打饼干是一种发酵饼干，它利用酵母的发酵作用和油脂的起酥效果，使成品质地酥松，其断面具有清晰地层次结构。苏打饼干中含有的苏打进入人体后可形成苏打水，苏打水具有弱碱性，有利于人体的酸碱平衡，并且有助于缓解消化不良和便秘症状，还具有抗氧化作用，能预防皮肤老化、增进食欲、美容养颜［1-2］。

苏打饼干生产过程中为了增加起酥效果，加入一定量的动物油脂和植物油脂，这些油脂中含有的不饱和脂肪酸具有不稳定性，在储藏过程中易发生氧化变质，给厂家带来一定损失。在影响茶苏打饼干变质的环境因素中，温度对品质影响最为重要，且是唯一不受食品类型和包装影响的因素。因此，建立以温度为基础的动力学模型用于预测［3］茶苏打饼干的货架期对控制质量的保藏期具有指导意义。目前用于产品货架期的预测主要有Arrhenius模型和Q10模型，这两种预测模型在山核桃、板栗、果仁、橄榄油等货架期的预测方面较为常见。杨虎清等［4］研究了不同温度下过氧化值、酸价及感官品质随时间的变化，并建立动力学预测模型；Kanavouras等［5］研究了不同包装材料和光照条件下橄榄油的储藏时间并建立动力学预测模型；任斯忱等［6］研究了核桃仁和花生仁中脂肪氧化的动力学变化并建立预测模型。

目前，对于苏打饼干保质期的研究多集中在静态分析，很少研究其酸败的动力学变化。本论文通过将茶苏打饼干敞口放置于24，34，44，54℃条件下的干燥箱中储藏，以过氧化值为控制指标，建立茶苏打饼干的动力学预测模型。本文在货架条件的选择上结合了加速试验［7］（ASLT），利用高温作为加速条件，在34，44，54℃储藏条件下采集数据，缩短实验周期，利用外推的方法求得在室温或低温储藏条件下的货架寿命，为其产业化产品保质期的预测提供参考。

1 材料及方法

1.1 材料和试剂

茶苏打饼干，实验室自制。

1.2 仪器和设备

冰乙酸、异辛烷、碘化钾、硫代硫酸钠、淀粉、石油醚（沸程：30～60℃）均为分析纯。

YXD-20K型远红外食品烤箱，广州鑫南方电热设备有限公司；FA1004型电子天平，上海精科天平仪器厂；JA21002电子秤，上海良平仪器仪表厂；HLS20型和面机，广东南海大沥德丰电热设备厂；FX-14型发酵箱，广州鑫南方电热设备有限公司；QM005型分体压面机，常州市墅乐厨具有限公司；DHP-9162型电热恒温培养箱，上海一恒科技有限公司。

1.3 实验方法

1.3.1 储藏实验

茶苏打饼干采用聚乙烯塑料袋封装，分为4组，每组10袋，每袋0.65 kg，分别于24，34，44，54℃的干燥箱环境中存储，每隔7 d测定其过氧化值。

1.3.2 过氧化值的测定

采用GB/T 5538—2005《动植物油脂过氧化值测定》方法测定过氧化值。

1.4 氧化动力学分析和货架期预测模型的建立

1.4.1 茶苏打饼干动力学模型的确立

茶苏打饼干中油脂品质的损失可用过氧化值的生成来表示

式（1）中，k为反应速率；n为反应级数。

将式（1）适当转换变化成时间t的函数即F（A）=kt，F（A）为茶苏打饼干的品质函数，不同反应级数对应不同的函数表达式，如表1。

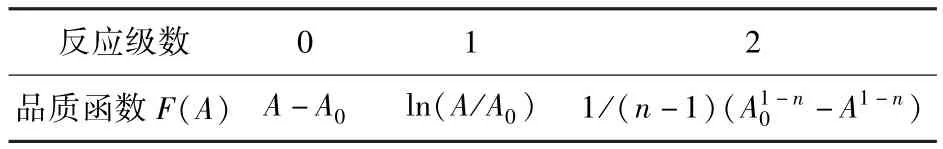
表1 不同反应级数下品质函数的表达式Tab.1 Functions of food quality under different reaction series

食品的油脂氧化属于一级反应［8］，本实验以过氧化值作为评价油脂氧化程度的指标，结合表1对式（1）变换得

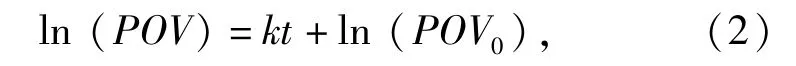
式（2）中，POV0和POV分别为初始过氧化值和储存t天后的过氧化值。

1.4.2 Arrhenius模型

Arrhenius方程是食品腐败速率和温度的函数关系［9-11］，在本实验中可以准确地描述油脂的氧化速率和温度T之间的关系。

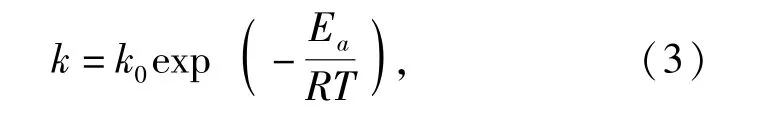
对式（3）取对数得到

式（3）和式（4）中，k0为频率因子；Ea为活化能（品质因子A变坏所需克服的能类）；R为气体常数，8.314 44 J/（mol·K）；T为热力学温度（K）。

根据式（4）知，求得不同温度下的反应速率常数取其对数（ln k）和热力学温度（1/T）作直线函数［12］，斜率即为。根据一级动力学反应方程和Arrhenius模型可以预测出茶苏打饼干的货架寿命即为：

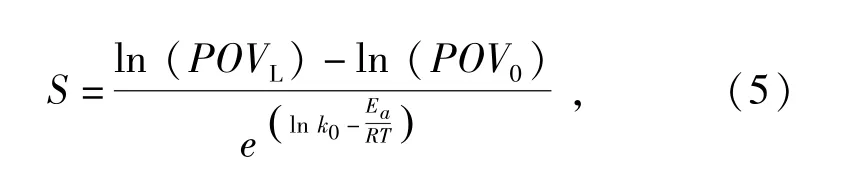
式（5）中，POV0和POVL为初始过氧化值和最大临界状态下过氧化值，S为货架模型的预测值，d。

1.4.3 Q10模型

Q10模型［13-16］的实质意义是温差为10℃，茶苏打饼干品质下降速率的比值，或货架时间延长的倍数，对于温度相差不是10℃，而是任意的温度T1和T2

对式（3）和式（6）变换可得到

对Arrhenius方程（3）取对数微分，然后在T1和T2范围内积分得到Ea、T、k三者间的关系。

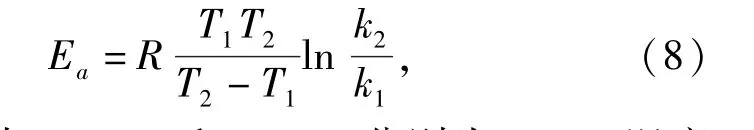
式（6）～（8）中：ST1，ST2和kT1，kT2分别为T1，T2温度下对应的储藏时间和反应速率。

1.4.4 Arrhenius和Q10模型预测差异性的比较

用上述两种模型预测28，38，48℃三个温度下的货架寿命，与真实寿命进行比较，确定最优预测模型。

2 结果与分析

2.1 茶苏打饼干储藏过程中POV的变化

过氧化值是衡量油脂氧化程度的指标，过氧化值的含量可表明油脂的变质程度，根据GB 7100—2003中规定，饼干类允许的最高过氧化值含量为0.25%。随温度的升高，油脂的氧化速率逐渐加快（见图1），在24，34℃条件下，储藏56 d过氧化值含量0.138%，0.211%，均低于国标规定的0.25%；在44℃条件下储藏至49 d过氧化值含量达到0.254%；而在54℃条件下储藏至35 d已经达到0.244%。可见高温对于脂肪的氧化有一定的加速作用。由于植物油脂中的不饱和脂肪酸含量较高，内部的双键不稳定，易受热断裂，形成自由基，引发脂肪的氧化；另一方面，高温加速了酶类对脂肪的水解，产生更多的游离脂肪酸。因此，高温不利于苏打饼干的储藏。

图1 不同储藏温度下茶苏打饼干过氧化值的变化Fig.1 Change of Peroxide value of tea soda crackers stored at different temperatures

2.2 一级动力学模型分析

一级动力学模型式（2）可表示为指数函数［17］：

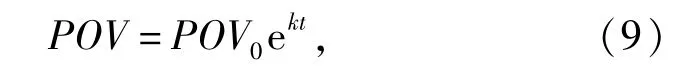
式（9）中，POV0，POV分别为初始过氧化值和储藏t时间后的过氧化值；k为反应速率。

实验数据以指数函数做回归方程分析，得到4个温度下过氧化值的动力学模型如表2。

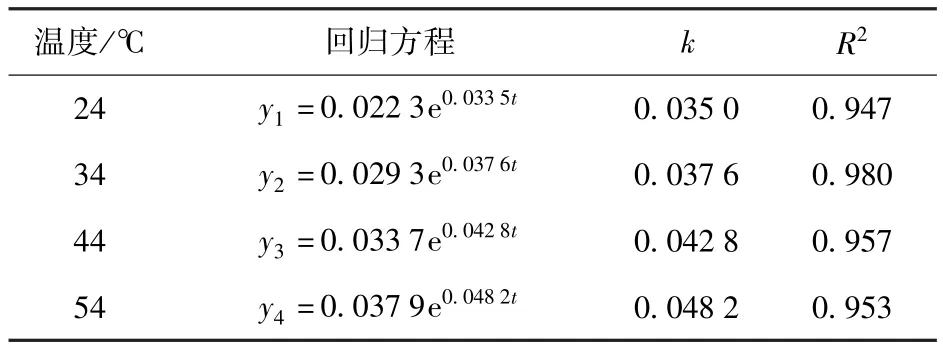
表2 茶苏打饼干在不同储藏温度下过氧化值的一级动力学方程Tab.2 First-order equation of POV change of tea soda crackers stored at different temperature

由表2知，4种温度下的R2均大于0.9，表明实验数据与方程的拟合较好，随着温度的升高k值逐渐增大，从0.035变化到0.482，表明氧化速率与温度密切相关。

2.3 Arrhenius预测模型的建立

求得不同温度下的k值，以ln k和热力学温度倒数1/T作图得到一条以为斜率的直线方程如表3和图2，可求得Ea和k0。

表3 温度与氧化速率的对应关系Tab.3 Corresponding relations between temperature and reaction rate

图2 温度与反应速率关系式的回归分析Fig.2 Regression analysis of temperature and reaction rate formula

结合式（4）和图2得到的直线回归方程为：lnk=-1 188.7x+0.593 6，R2=0.999，表明该方程具有可靠性，得到Ea=9 883.38 J/mol，能够准确描述ln k和1/T之间的关系。结合（5）式可得出茶苏打饼干的货架期预测公式为：

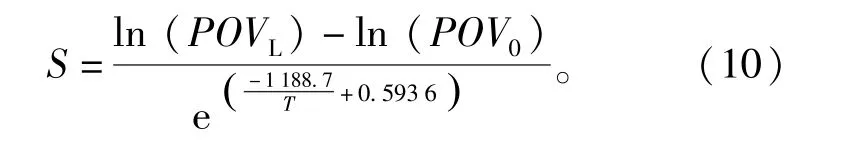
2.4 Q10预测模型的建立

由4个温度点平均取3个温度范围297.5～307.5 K（24～34℃）、307.5～317.5 K（34～44℃）、317.5～327.5 K（44～54℃），将国标规定的饼干类食品最大过氧化值临界值0.25 g/100 g带入到式（2）中得到4个温度下的货架时间为t1=73 d，t2= 61 d，t3=51 d，t4=42 d。根据式（8）、式（7）和式（6），分别得到对应范围的Ea、Q10和预测公式ST如表4。

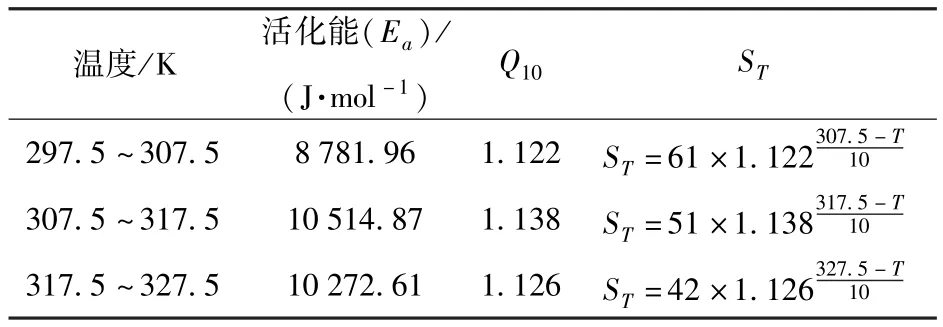
表4 茶苏打饼干在3个温度范围内的Ea和Q10预测模型Tab.4 Eaand Q10prediction models of tea soda crackers in three temperature range

2.5 外推法［18-19］

货架寿命在一定温度（或时间）下，随着时间（或温度）变化，呈现出上升或者下降的趋势，而Q10方程和Arrhenius方程价值在于可在较高温度下收集数据来求得较低温度下的货架寿命，因而很好地反应出这种变化。因此用建立的预测模型y=f（t）可外推出低温下的数据。

2.6 Arrhenius模型和Q10模型预测差异性

利用Arrhenius模型和Q10模型可以预测一定温度范围内任意温度下茶苏打饼干的货架寿命，取28，38，48℃三个温度下储藏茶苏打饼干，验证两个模型预测的准确性，并比较二者的相对误差，找出最优的预测模型。比较结果如表5。

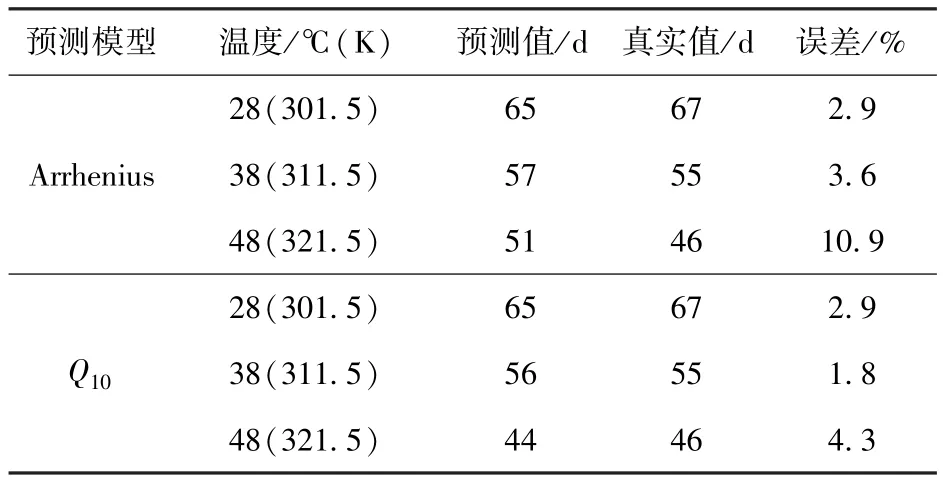
表5 茶苏打饼干动力学预测模型值与真实货架寿命的比较Tab.5 Comparison between values of dynamic models prediction and actual shelf life of tea soda crackers

Arrhenius模型和Q10模型对于茶苏打饼干的预测比较接近，在28℃和38℃条件下预测的准确性比较高，Arrhenius模型的预测误差为2.9%和3.6%，Q10模型的预测误差为2.9%和1.8%；在48℃条件下，Arrhenius模型的预测误差达到10.9%，与真实值有了一定偏差，而Q10模型的预测误差为4.3%，可较好地反应该温度下的货架寿命。因而，Q10模型对于茶苏打饼干货架期的预测更为准确。

2.7 讨论

两种预测模型产生误差大小的原因，是由于活化能Ea发生改变。在温度较低，变化范围较小的情况下，活化能Ea几乎不发生改变，可以作为一个定值运用到预测方程中。若温度较高，跨度较大的情况下，活化能Ea将不再作为定值用来预测茶苏打饼干的货架期。相比于Arrhenius模型中Ea的固定不变，Q10模型是在3个不同的温度范围内得到不同的Ea，减少了温度跨度对预测误差的影响。Q10模型更能准确反应货架寿命和温度之间的关系。

3 结 论

［1］赵红玉.基于酸性体质浅谈中医药治病原理［J］.江西中医学院学报，2008，20（4）：89-90.

［2］王晓娇.碱性负离子水对酸性体质的影响［D］.大连：辽宁师范大学，2013.

［3］Torrieri E，Russo F，Di Monaco R，et al.Shelf life prediction of fresh Italian pork sausage modified atmosphere packed［J］.Food Sci Technol Int，2011，17（3）：223-232.

［4］杨虎清，吴峰华.山核桃基于温度变化的储藏寿命预测［J］.食品科学，2010，31（12）：274-278.

［5］Kanavouras A，Coutelieris F A.Shelf-life predictions for packaged olive oil based on simulation［J］.Food Chemistry，2006，96（5）：48-55.

［6］任斯忱，李汴生，沈晓曦，等.花生仁与核桃仁储藏货架期预测模型［J］.食品科学，2012，33（14）：290-295.

［7］García-García P，López-López A，Garrido-Fernandez A. Study of the shelf life of ripe olives using an accelerated test approach［J］.Journal of Food Engineering，2008（4）：569-575.

［8］余晓琴，车晓彦.食品货架寿命预测研究［J］.食品研究与开发，2007，28（3）：84-87.

［9］Koca N，Burdurlu H S.Kinetics of colour changes in dehydrated carrots［J］.Journal of food engineering，2007，78：449-445.

［10］Kristenen D，Hansen E，Arndal A，et al.Influence of light and temperature on the colour and oxidative stability of processed cheese［J］.Int Dairy J，2001，11（10）：837-843.

［11］Labuza T P.Shelf-life dating of foods［M］.Westport：Food and Nutrition Press，1982：211-234.

［12］支红波，韩永生.含油脂食品货架寿命研究方法［J］.中国包装工业，2005（11）：72-73.

［13］蔡燕芬.食品储存期加速测试及其应用［J］.食品科技，2004（3）：80-82.

［14］Calligaris S，Manzocco L，Kravina G，et al.Shelf-life modeling of bakery products by using oxidation indices［J］.Journal of Agricultural and Food Chemistry，2007，55（5）：2004-2009.

［15］申晓曦.果仁糖果用果仁的加工与储藏特性研究［D］.广州：华南理工大学，2011.

［16］杨宏顺，冯国平，李云飞.嫩茎花椰菜在不同气调储藏下叶绿素和维生素C的降解及活化能的研究［J］.农业工程学报，2004，20（4）：172-175.

［17］Guerra S，Lagazio L，Manzocco L，et al.Risks and pitfalls of sensory data analysis for shelf life prediction：data simulation applied to the case of coffee［J］.LWTFood Science and Technology，2008，41：2070-2078.

［18］潘云翔，管翔颖，冯增媛，等.一种确定固相机理函数的新方法—固态草酸镍（Ⅱ）二水合物脱水过程的非等温动力学［J］.无机化学学报，1999，15（2）：247-251.

［19］Lu Shanwang，Yu Zhongzhang，Pei Jigao.A novel function for the cellulose binding module of cellobiohydrolasel［J］.Science in China Series C：Life Sciences，2008，51（7）：620-629.

Establishment of Shelf-life Prediction Model for Tea Soda Crackers

LI Xinwang， ZHANG Jing， LI Xueying， XU Hui， LU Ning*
（College of Tea and Food Science and Technology，Anhui Agricultural University，Hefei 230036，China）

Two mathematical models were used to predict the shelf life of tea soda crackers and compare error value and the optimal model was determined.Base on the theory of first-order kinetics model，the peroxide values of tea soda crackers stored at different temperatures（24，34，44，54℃）were studied. Moreover，the correlation between the storage temperature and reaction rate of peroxide value was established using the Arrhenius equation and Q10equation and the shelf life of tea soda crackers stored at different temperatures（28，38，48℃）were compared with the real values.The results showed that the maximum prediction errors of the Arrhenius model and Q10model were 10.9%and 4.3%.Therefore，the Q10model could be used to establish the correlation between the shelf life and temperature.Compared with the Arrhenius model，the Q10model had the higher precision to predict the shelf life of tea soda crackers.

kinetic model；peroxide value；shelf life

檀彩莲）

TS278；TS213.2

A

10.3969/j.issn.2095-6002.2015.02.015

2095-6002（2015）02-0074-05

李新旺，张晶，李雪影，等.茶苏打饼干货架寿命预测模型的建立［J］.食品科学技术学报，2015，33（2）：74-78.

LI Xinwang，ZHANG Jing，LI Xueying，et al.Establishment of shelf-life prediction model for tea soda crackers［J］.Journal of Food Science and Technology，2015，33（2）：74-78.

2014-11-11

李新旺，男，硕士研究生，研究方向为农产品加工及储藏工程；

*陆 宁，女，教授，博士，主要从事食品及农产品贮藏与加工方面的研究。

。