图形变换中的“万变不离其宗”

□江苏省苏州工业园区星海实验中学　戴小驹

图形变换中的“万变不离其宗”

□江苏省苏州工业园区星海实验中学戴小驹

图形变换是初中数学中极其重要的内容，包括两类：一类是“刚性变换”（全等变换），即图形的形状、大小不变，只是位置上发生了变化，如平移、旋转、轴对称（折叠）等；另一类是“弹性变换”，即图形的形状、大小、位置都发生了变化，如相似变换（放大或缩小）、动点、动线、动面等。

一、万变不离其宗之一：面积和周长的不变

1.变换手段1：平移。

【教学片段】已知：长方形草坪水平方向长为a米，竖直方向长为b米。现欲在其中铺设黄色瓷砖小路。

师：如图1操作。在图1中将A1A2向右平移1米到B1B2，得到封闭图形A1A2B2B1（即黄色瓷砖小路部分）。猜想：除去黄色瓷砖小路部分后剩余部分的草地面积为S=_______？

探究并说明理由：_____________________？

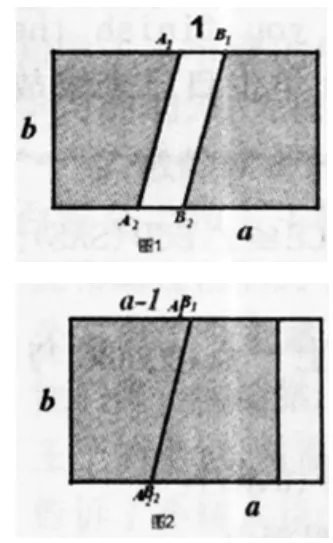
生1：剩余部分的草地面积为S=长方形的面积-□A1A2B2B1的面积=ab-b。

师：很好，我们称这种方法为直接法，还有其他方法吗？

（大部分学生面面相觑，这时一个聪明的孩子站起来说——）

生2：我可以把右边草坪平移到左边（如图2），

这样S=绿色长方形的面积=（a-1）b=ab-b。

师：真棒！这种方法称为间接法……

（还没等老师说完，生1就不服气地站起来说——）

生1：我的方法也很棒啊！（老师微笑予以肯定）

师：下面我把马路变成图3、图4、图5的形状，依然保持马路宽为1米，你还能用直接法求草地面积S吗？（全体学生沉思中……好像不能解决）

师：那间接法呢？

生3：我会！跟上面一样把右边草坪平移到左边（如图2），这样S=绿色长方形的面积=（a-1）b=ab-b。

（全体学生鼓掌！）

图3

图4

图5

图6

【反思】尽管小路设计的形状不一，但其面积却始终保持不变。因此，我们常常利用这种平移中的不变性，巧妙地求一些不规则图形的面积。

【延伸】

1.矩形ABCD中，横向黄色阴影部分是矩形，另一部分是平行四边形，依照图中标注的数据，图中空白部分的面积为_______________？（简单方法：图7平移至图8）

2.如图正方形ABCD、正方形CDEF的边长都为5，求图中黄色阴影部分的面积为________？

（简单方法：图9平移至图10）

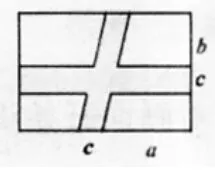
图7

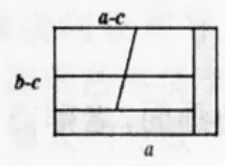
图8

图9

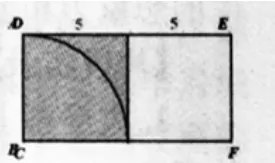
图10

2.变换手段2：旋转。

【教学片段】已知：一正方形纸片ABCD边长为a。

师：（操作）（1）找出ABCD的对称中心为O；（2）用一张与该正方形ABCD同样大小的正方形OEFG，其顶点放在O点处。将其旋转并猜想：在旋转过程中两正方形重叠部分（即黄色部分）的面积将怎样变化？并说明理由（老师先给图11，接着操作几何画板给出图12、13、14）。

生：可以证明△OPC≌△OQD（ASA），所以可以旋转△OPC到△OQD，把不规则的图形转化成规则的△ODC的面积。（如图15）

【反思】尽管在旋转的过程中，重叠部分的形状在不断地发生改变，但其面积却始终保持不变。因此，我们常常利用这种旋转的不变性，巧妙地求一些不规则图形的面积。

图11

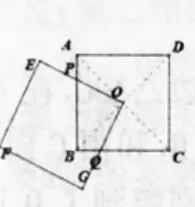
图12

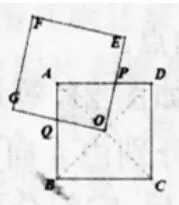
图13

图14

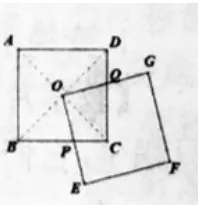
图15

【延伸】如图点P为正方形ABCD内的一点，连PA、PB，将△PAB绕点B顺时针转90度到△P'CB的位置，设AB=2，PB=1，求旋转过程中PA所扫过的

区域（黄色阴影部分）的面积为_____________？

（方法：图16旋转至图17）3.变换手段3：动点。

【反思】尽管点（可以是单动点、双动点）在运动，图形的形状甚至时刻在不停地发生变化，但其面积或面积间的关系，有时在特定的条件下却有可能始终保持不变。此类动点中的不变性有时隐藏得较深，需要通过计算方可发现。这种数形结合的思想，在数学中很重要。

二、万变不离其宗之二：形状的不变

1.变换手段1：双动点。

【教学片段】已知：如图21，等边△ABC，在A、C处各有一只蜗牛，它们同时同速分别由A向B，和由C向A爬行，经过t分钟后，它们分别爬到了D、E处，设DC交BE于F。

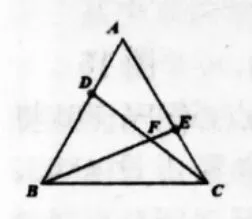
（1）说明：△ACD≌△CBE。

（2）猜想：∠BFC的大小在蜗牛爬行的过程中变化吗？为什么？

【分析与解】尽管在蜗牛爬行的过程中，点的运动带动了整个图形的变化，但只要我们细心，还是会发现△ACD与△CBE间的全等关系以及∠BFC=120°却始终保持不变。

2.变换手段2：动面（借助几何画板工具）。

【教学片段】问题1：如图22，C为线段BE上一点，△ABC与△CDE是等边三角形，求证AE=BD。

问题1的变化：如图23、24、25所示，C不再是线段BC上一点，△ABC与△CDE是等边三角形猜想：

你刚才得到的AE与BD的大小关系的结论还成立吗？

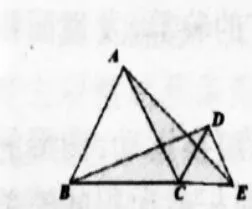
图22

图23

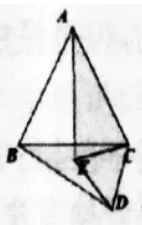
图24

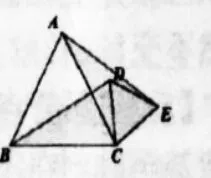
图25

【分析与解】所有情况都可以证明△ACE≌△BCD（SAS），以不变应万变。

问题2：如图26所示，C为线段BC上一点，△ABC与△CDE是等边三角形，

（1）操作：分别取AB、BE、ED、DA的中点F、G、H、I；

（2）试探究：四边形FGHI的形状，并说明理由。

问题2的变化：如图27、28、29所示，当△CDE绕点E旋转时，试探究：上述结论还成立吗？

（变化实现工具：几何画板拖动点D旋转一周，产生无数种变化图形）

图26

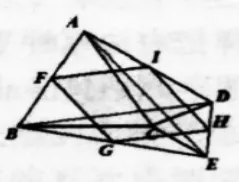
图27

图28

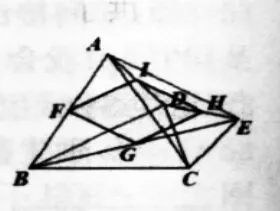
图29

【分析与解】由上一题可知无论图形怎样变化，总有AE=BD，再根据中位线、中点四边形定理可证四边形FGHI始终为菱形。

图形变换的综合题，一直是中考中的难点。但需要注意的是，不管是“刚性变换”，还是“弹性变换”，一定要根据题意，画出图形，变动为静，数形结合，找出图形的特点及隐含条件，撇开形式上的变化多端，找寻其不变的数学本质，使问题迎刃而解。