初中数学教学中如何渗透分类讨论的思想
2015-11-09江苏省苏州市平江中学校陆洋
□江苏省苏州市平江中学校 陆洋
初中数学教学中如何渗透分类讨论的思想
□江苏省苏州市平江中学校陆洋
在中学数学教学中,分类讨论的重要性十分突出。分类讨论不仅是解决数学问题的一种策略,还是训练学生思维方法、培养其思维能力的重要手段。文章从日常教学出发,对分类的原因、分类讨论的标准、步骤及掌握分类讨论的方法进行了归纳。
初中数学分类讨论专题训练
初三中考复习时,教师们会发现那些具有开放性、探索性较强的试题往往是各地中考的压轴题,而考生往往会失分很多。究其原因,分类讨论思想缺失是一个重要方面。
一、日常渗透,培养学生分类讨论的意识
对于几何类型的分类讨论,在平时课上要训练学生自己画出几何图形,特别是读题画图。只有对图形有很好的感觉,才会对分类讨论有着最直接的帮助。
【例1】如图1,在正方形ABCD中,AB=3cm,动点P自A点出发沿折线AD-DC-CB以每秒3cm的速度运动,到达B点时停止运动。设△ABP的面积为y(cm2),运动时间为x(秒),则表示y与x之间函数关系的是。

图1
如图所示,由动点P的运动路径可知,可以分为三个情况:P在AD上,P在DC上,和P在CB上。根据三角形面积公式,只要找出三角形的底和高,就可以把这题做出来。自变量x的取值范围根据边长和动点P的速度,用路程=时间×速度,求出动点P到临界点D和C的所用时间即可。有些学生没有画图的习惯,想来想去一筹莫展,或者漏解,或者自变量取值范围不恰当。动手画图能力强的学生,思路应该是很清晰的,只要按照P的运动轨迹,分类就出来了。要引导学生从起点开始画,还要特别关注各临界状况,因为这是求自变量取值范围的关键。
二、揭示规律,引导学生掌握分类讨论的思想方法
引导学生分析特点、把握规律至关重要。分类通常有以下四个基本步骤:一是确定分类对象;二是根据题目特点合理分类;三是依据分类逐项讨论;四是归纳分类结果得出答案。但要做到正确分类,还必须坚持几个原则:(1)分类中的每一部分是相互独立的;(2)一次分类按一个标准;(3)分类讨论应逐级进行。
【例2】如图2,在平面直角坐标系中,四边形ABCD是梯形,BC∥AD,∠BAD+∠CDA=90°,AD在x轴上,点A的坐标(-1,0),点B的坐标(0,2),BC=OB。(1)求过点A、B、C的抛物线的解析式;(2)动点E从点B(不包括点B)出发,沿BC运动到点C停止,在运动过程中,过点E作EF⊥AD于点F,将四边形ABEF沿直线EF折叠,得到四边形A1B1EF,点A、B的对应点分别是点A1、B1,设四边形A1B1EF与梯形ABCD重合部分的面积为S,F点的坐标是(x,0),求S 与x的函数关系式。
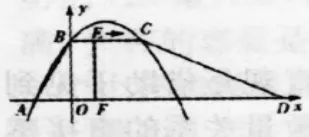
图2
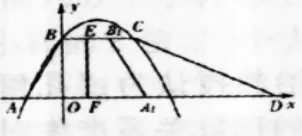
图I
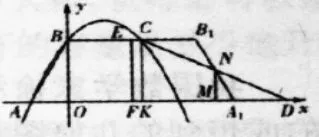
图II
对于这道题,分类的关键就是如何根据EF的位置不同或者说根据重合部分的形状不同而确定出不同的图形。因此,要鼓励学生在原图的基础上,从起点出发,画出运动后不同类型的图形,确定出导致分类的关键因素,再经过分析完善分类,如图I、II所示,最后进行计算。
三、专题训练,培养学生解决综合问题的能力
初中数学中的分类讨论思想无处不在,一般地,分类情况可分为:(1)数学概念的内涵需要分类讨论;(2)问题中的条件需要分类讨论;(3)问题中的变量需要分类讨论;(4)形状、位置的变化需要分类讨论。面对诸多的类型,教学时如果能进行专题训练,这样学生就会掌握不同类型的分类,将会大大提高他们解决综合问题的能力。
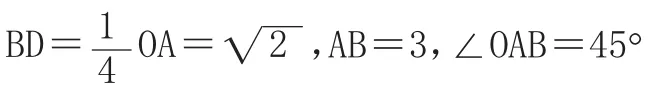
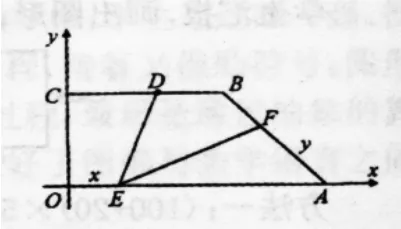
(1)直接写出D点的坐标;(2)设OE=x,AF=y,试确定y与x之间的函数关系;
(3)当△AEF是等腰三角形时,将△AEF沿EF折叠,得到△A'EF,求△A'EF与五边形OEFBC重叠部分的面积。
首先指导学生根据△AEF是等腰三角形,将本题分为EF=AF、EF=AE或AF=AE三种情况;再引导学生发现本题中的一些特殊角,如∠OAB=45°、∠DEF=45°等,然后根据这些关键的要素画出正确的示意图,从而揭示出三种情形下图形的本质,面积也就迎刃而解了。
在数学教学中,我们既要重视数学知识应用阶段的教学,更要重视形成阶段的教学,把数学思想方法的训练贯穿于教学始终,充分揭示数学思维过程,将“发现过程中的数学”返璞归真地教给学生,这才是数学教学追寻的最终目的。
