GPU上高光谱快速ICA降维并行算法*
2015-11-07方民权周海芳张卫民申小龙
方民权,周海芳,张卫民,申小龙
(国防科技大学 计算机学院, 湖南 长沙 410073)
GPU上高光谱快速ICA降维并行算法*
方民权,周海芳,张卫民,申小龙
(国防科技大学 计算机学院, 湖南 长沙 410073)
高光谱影像降维快速独立成分分析过程包含大规模矩阵运算和大量迭代计算。通过分析算法热点,设计协方差矩阵计算、白化处理、ICA迭代和IC变换等关键热点的图像处理单元映射方案,提出并实现一种G-FastICA并行算法,并基于GPU架构研究算法优化策略。实验结果显示:在处理高光谱影像降维时,CPU/GPU异构系统能获得比CPU更高效的性能,G-FastICA算法比串行最高可获得72倍加速比,比16核CPU并行处理快4~6.5倍。
图像处理单元;高光谱影像降维;快速独立成分分析;并行算法;性能优化
(CollegeofComputer,NationalUniversityofDefenseTechnology,Changsha410073,China)
高光谱遥感技术广泛应用于军事、农业、环境科学、地质、海洋学等领域,这些领域迫切要求及时处理[1]。但高光谱影像数据有波段多、数据量大、相关性强、冗余多等特点,直接处理将导致维数灾难、空空间现象等严重的计算问题[2-4]。因此,国内外专家学者处理高光谱影像数据过程常常包括降维步骤。降维通过一定的映射,将高维影像数据转换成低维影像数据,并保持信息量基本不变。
高光谱影像降维方法可分为线性和非线性两大类:线性降维有主成分分析(PrincipalComponentAnalysis,PCA)[5]、独立成分分析(IndependentComponentAnalysis,ICA)[6]等方法;非线性降维包括基于核的方法和基于流行学习的方法,如等距映射法(ISOmetricMAPping,ISOMAP)[7]、局部线性嵌入(LocallyLinearEmbedding,LLE)[8]等。独立成分分析是应用最广泛的降维方法之一,其降维过程包含了大规模矩阵计算和大量迭代运算。由于高光谱影像波段多、数据量大等特征,降维处理过程复杂且耗时,传统的串行降维已无法满足各行业的需求,因此并行降维的研究已迫在眉睫。
自2007年Nvidia正式推出统一计算设备架构(ComputeUnifiedDeviceArchitecture,CUDA)以来,图像处理单元在通用计算领域发展迅猛。CPU/GPU的异构系统可编程性好、性价比高、功耗比低,已成为高性能计算领域的黑马。搭载这种异构系统的天河1A和泰坦分别在2010年和2012年夺得TOP500榜首[9]。CPU/GPU异构系统的快速发展为高光谱影像降维的实时处理提供了可能。
高光谱影像并行处理在传统并行系统中已有成熟的应用,David等[10]基于异构讯息传递接口(MessagePassingInterface,MPI)在网络集群系统研究了高光谱影像处理的技术;Javier等[11]提出基于神经网络的高光谱影像并行分类算法。在CPU/GPU异构系统上,Sanchez等[12]对高光谱解混进行了GPU移植;Yang等[13]利用多GPU实现了高光谱影像快速波段选择;Rui等[14]在GPU上实现FastICA算法,加速55倍;Jacquelyne等[15]用OpenCL在GPU上实现InfomaxICA,最高加速56倍。但这些研究较少涉及基于GPU研究高光谱影像降维。本文研究基于负熵最大的FastICA降维算法[16-17],针对算法热点设计GPU映射方案,最终提出并实现一种G-FastICA并行算法。
1 FastICA算法与热点分析
1.1 基于负熵最大的FastICA
FastICA算法有基于负熵最大、基于似然最大、基于峭度3种形式,本文主要研究基于负熵最大的FastICA算法。该算法是盲源降维方法,以负熵最大为搜寻方向,实现独立源的顺序提取,采用定点迭代的优化方法,收敛更加快速、稳健[16-17]。
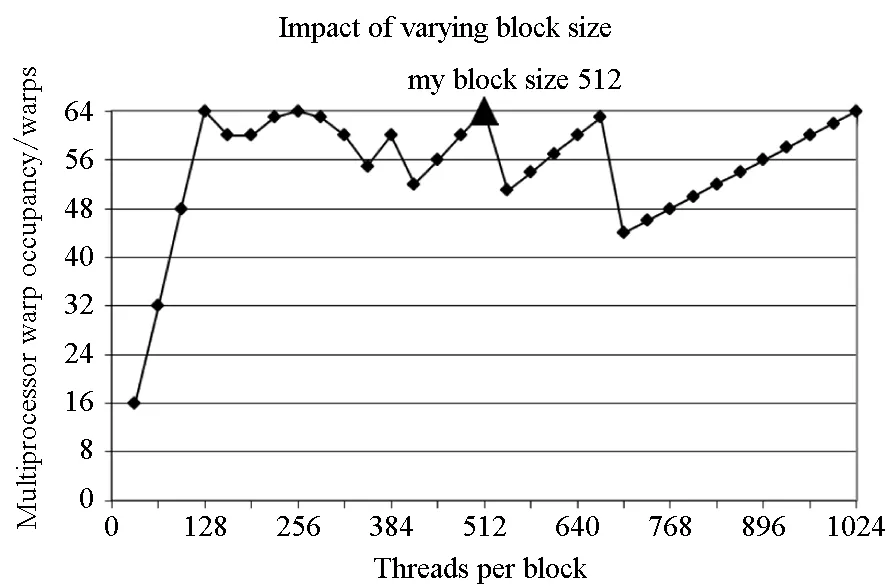
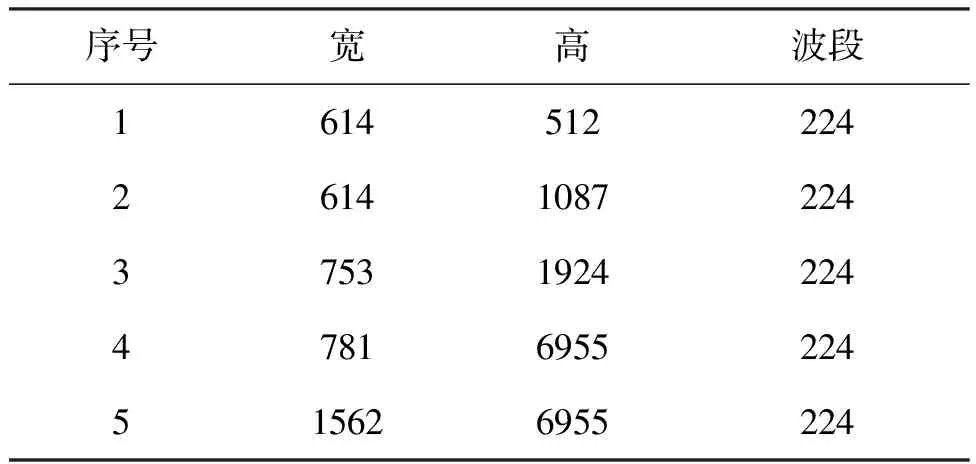
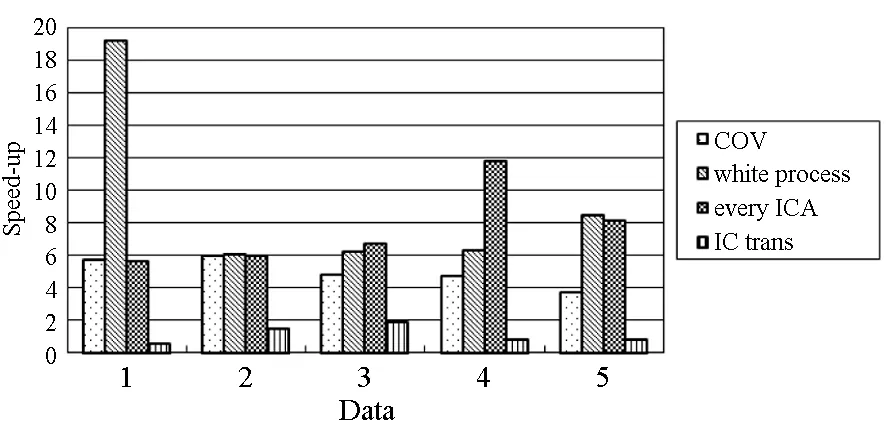
对于高光谱影像数据X(W×H×B,宽W、高H、波段B),X可视为B行S列(S=W×H)的二维矩阵,矩阵的一行表示一个波段的高光谱影像数据。通过独立成分分析方法降维,可以获得m个IC图像,其中m step1.计算X的协方差矩阵; step2.计算协方差矩阵的特征值及特征向量,并根据阈值T选取最终IC图像数量m; step3.计算白化矩阵M=D-1/2VT,其中D为X的特征值矩阵,V为对应的特征向量矩阵; step4.高光谱影像数据白化处理Z=MX,X要减去均值(即零均值处理),M为白化矩阵,Z为白化处理结果矩阵; step5.迭代开始: ①初始化Wi,Wi为变换矩阵W的一列; 其中g为非线性函数,经测试,取g(y)=y3可更稳定、更快地达到ICA迭代收敛。 ④归一化Wi=Wi/‖Wi‖; ⑤判断是否收敛,不收敛则返回到步骤②,若收敛,如果所有的Wi已经计算结束(即i=m),则退出,否则令i=i+1,返回到步骤①计算Wi; step6.计算独立成分Y=WZ; 1.2 加速热点分析 实现串行高光谱影像FastICA降维算法,对宽781、高6955、波段数224的高光谱影像降维,测试并统计各步骤占总计算时间的比率(见表1)。表中数据显示,协方差矩阵计算(COV)、白化处理(whiteprocess)和ICA迭代(ICAiteration)过程比重较大,共占总计算时间的99%,是并行研究的关键热点。此外特征值计算取决于波段数B,本文数据波段数均为224,因此特征值特征向量的计算属于不变串行分量,无须考虑并行;IC变换(ICtransformation)、数据I/O与高光谱影像数据的宽、高、波段数及其信息特征相关,作为次要热点考虑其并行化。 表1 FastICA时间分布 2.1 协方差矩阵计算的GPU映射 协方差矩阵是对称阵,仅需计算其下三角元素,再将值填入对应的上三角阵。针对该过程,设计了一种映射方案:GPU上的每个线程块完成协方差矩阵中一个协方差的计算任务,如图1所示。启动B×(B+1)/2个block,每个block中的thread数量可根据occupancy选取最佳的thread数。其思想是将协方差矩阵中单个协方差的计算任务映射到对应的block中,由一个block完成一个协方差元素的计算。一种实现策略是:每次启动维度为<< 图1 协方差矩阵的GPU映射方案Fig.1 GPU mapping scheme of covariance matrix 2.2 设备端并行白化处理 GPU是细粒度并行协处理器,在白化处理中寻找细粒度的并行计算任务,再将这些细粒度计算任务通过kernel函数映射到GPU核上执行,这是设备端并行白化处理的关键。 在白化处理(Z=MX)中,M是B×m的矩阵,X的尺寸为S×B,结果矩阵Z大小为S×m。结果矩阵每个元素的计算是独立的,且计算任务量类似,是长为B的向量内积。高光谱影像的波段数B一般为几十到上百不等,即向量内积的运算量有限,是细粒度任务,故视结果矩阵的单个元素的计算为单元任务,将其映射到GPU的thread上。整个结果矩阵共有S×m个单元任务,需要S×m个线程参与计算;但高光谱影像的宽W和高H较大(约数百到上千),故S=W×H较大,S×m的数量级更大,超过GPU一次可启动的最大线程数量,无法直接运算。此时,采用循环计算的方法,即启动适当数量的block和thread,多次循环完成计算任务。对于线程块blockIdx中的线程threadIdx,需计算索引为i×(gridDim×blockDim)+blockIdx×blockDim+threadIdx的任务(i为循环变量),直到索引超过S×m。该方案中,gridDim和blockDim不受算法自身约束,可根据occupancy自由设定,以最大化GPU设备占用率,从而获得最佳性能。 2.3 ICA迭代的GPU移植 ICA迭代过程中,受数据依赖限制,不同迭代无法同时运算,只能在单次迭代中开发并行。分析迭代中各个步骤的计算量,初始化、正交化、归一化和判断操作的计算量很小,可不必考虑,主要的计算量集中在步骤②中。分解该步骤,抽象得到图2所示的ICA迭代宏观模型。 图2 ICA迭代关键步骤模型Fig.2 Model of key step for ICA iteration 2.4 G-FastICA算法 IC变换与白化处理的运算模型类似,因此将前文设计的白化处理并行策略套用到IC变换中。高光谱影像数据I/O的并行化依赖于并行文件系统或缓存机制,利用多线程技术,每个线程创建独立的文件指针,通过合理的数据分割,各个线程将指针指向各自的目标位置,再进行输入输出操作。 针对单GPU,根据前面提出的协方差矩阵计算、白化处理、ICA迭代、IC变换等热点的GPU映射并行方案,用其替代串行算法的对应步骤,可实现CPU与GPU协同计算高光谱影像FastICA降维过程,称之为G-FastICA算法。 基于GPU的计算通信重叠优化:协方差矩阵计算,存在着计算通信重叠的可能性。由图1可知,第i行计算使用高光谱影像数据前i个波段的数据。传输完第1个波段数据后,协方差矩阵第1行计算和第2波段数据传输可同时进行,此时计算与通信能够重叠。采用多流的方法实现GPU计算与CPU/GPU通信的并发执行。得益于计算通信重叠,几乎能掩盖全部高光谱影像数据传输时间。 GPU存储优化:GPU提供了层次分明的存储单元系统,按离核距离由近及远分别是寄存器、共享存储器、全局存储器,可以显示这些存储单元的使用。离核距离近的延迟低,访存效率高,因此应尽量使用离核近的存储单元。本文通过下面两项技术对各并行热点GPU进行优化(GPU映射设计时已保证访存对齐):①共享存储访问取代全局存储访问;②采用寄存器存储数量较少的中间变量。通过这两个步骤修改,各热点均能获得部分性能提升,效果见表2(优化手段0表示无优化,1采取GPU存储优化手段1,2在1基础上采用GPU存储优化手段2,3在2基础上增加计算通信重叠优化)。表中数据显示了本文优化效果。 表2GPU存储优化技术效果 Fig.2EffectsofstorageoptimizingmethodonGPU ms 最佳维度设计:GPU是众核架构,细粒度并行,对于线程数量非常敏感,因此需要合理设计线程维度来保证GPU性能发挥。GPU上的线程数量可以是任意的,全部测试是不可能的,需要一套理论指导线程数量的选择。本文设计了一种线程维度选择方法,步骤如下: 1)计算kernel的GPU设备占用率(occupancy); 2)选择占用率最高的几个线程数量进行实验测试,择优选取。 GPU设备占用率是发挥GPU性能的一项重要指标,主要受限于活动的warp数目,而活动的warp数目与使用的寄存器、共享存储器有关。通过统计kernel函数使用的寄存器数量和共享存储器容量,可以计算出可活动warp的数量,再根据warp数量与线程数量关系图,可以初步选定几个占用率高的线程数量。针对上述选取的线程数量逐一进行实验测试,对比性能,可得到最佳线程维度。 比如在协方差矩阵计算中,每个thread需要18个寄存器,每个block需要3072byte的共享存储,对GPU的最大活动warp数量进行分析,通过计算可知,寄存器和共享存储器的数量都不会限制warp数量;此时,warp数量受最大warp数量限制,与线程数量有关,其关系见图3。选择线程数量128,256,512,1024时,活动warp数量达到最大64,occupancy达到100%。再对这4个线程维度进行实验测试,统计并对比结果数据,获得最佳线程维度。 图3 线程数量对warp数量的影响(协方差)Fig.3 Effect between threads and warps(COV) 计算所有GPU并行热点occupancy,选择线程数量使得活动warp数量最大化,测试并统计其结果,见表3。表中数据显示,当线程数量为1024时,白化处理可以获得最高性能;其他热点在线程数量为512时性能最佳。 表3 线程数量对性能的影响 4.1 实验平台与测试数据 本文用统一计算设备架构(ComputeUnifedDeviceArchitecture,CUDA)技术实现上述GPU并行映射方案和优化策略。其中涉及的矩阵、向量运算均手动实现,未使用cublas库,主要有以下几个方面的考虑:1)空间复杂度,cublas库要求数据类型是float,而高光谱影像数据类型为unsignedchar,如需转换将增加3倍存储空间,可能超过GPU全局存储容量,导致无法处理;2)除开unsignedchar到float类型的转换开销,GPU或集成众核(ManyIntegratedCore,MIC)等协处理器访问unsignedchar类型的延迟比float类型小很多;3)cublas库函数任务无法拆分,必须先通信后计算,将导致无法使用计算通信重叠的优化策略;4)由于高光谱数据的特点,矩阵运算不规整,用通用方法优化的cublas未必能获得更好的效果。 实验采用当前主流的GPU微型超算平台,搭载2个8核IntelXeonE5-2650CPU和nVidiaTeslaK20GPU。软件平台采用LinuxCentOS6.2操作系统、GCC4.4.6编译器、CUDA5.0工具包。 本文采用表4罗列的5组机载可见光成像光谱仪(AirborneVisibleInfraredImagingSpectrometer,AVIRIS)高光谱影像数据。数据已经过预处理,把16位int型光谱信息转换为unsignedchar类型的像素信息。 表4 高光谱影像数据详细信息 关于ICA迭代次数的约定:由于高光谱影像数据和ICA迭代过程中取得的随机数不同,ICA迭代次数也将有所差异,不同的迭代次数导致时间消耗不可比。为了较准确地对比算法性能,本文做出如下约定:相同的数据取固定的迭代次数。通过多次实验取平均值的方法,确定各组数据的迭代次数(见表5)。 表5 高光谱数据迭代次数 4.2 两种测评基准 本文从最优串行和CPU满负载并行两个方面对算法性能进行测评。 1)最优串行程序。表6分别罗列了开启优化开关O0,O1,O2,O3时,处理高光谱影像数据1的时间。优化开关为O2时,串行程序执行时间最短,作为与并行算法对比的标准。 表6 串行程序优化执行时间表 本文通过对比线程级和进程级并行程序的性能,采取性能较好的CPU并行方案作为CPU满负载并行标准。本文分别采取OpenMP多线程并行和MPI多进程并行,实现这两种并行FastICA降维算法,测试性能并比较,见表7。对比表中数据,MPI并行程序能获得更好的性能,因此本文以MPI并行FastICA程序作为CPU满负载并行程序。 表7 CPU并行程序加速效果 4.3 GPU对CPU的性能优势 图4 各热点GPU与串行加速比Fig.4 Speed-up between GPU and serial 统计G-FastICA高光谱影像降维算法中各步骤的耗时信息,对比最佳串行程序(见图4)和MPI并行程序(见图5)。图4数据显示,本文设计的各热点GPU映射方案能获得比串行快几十倍的加速比,其中协方差矩阵计算加速近50倍,白化处理加速300倍左右,ICA迭代过程加速42~109倍不等,IC变换可加速19~41倍。图5显示GPU相对CPU在并行计算上更有优势,本文设计的GPU映射方案比CPU并行版本(MPI)效率更高,其中协方差矩阵计算GPU比CPU快4~6倍,白化处理加速6~8倍,ICA迭代中GPU比CPU快8~11倍,IC变换由于计算量较小,GPU和CPU性能差距不大。 图5 各热点GPU与CPU并行加速比Fig.5 Speed-up between GPU and CPU 图6统计了G-FastICA算法对最佳串行程序、MPI并行程序总时间的加速比。图中数据显示,G-FastICA算法比串行FastICA算法加速36~72倍不等;G-FastICA算法比MPI并行算法加速4.1~6.5倍不等。这说明在高光谱影像降维FastICA处理时,CPU/GPU异构系统能比CPU并行系统获得更好的性能。 图6 G-FastICA与串行和MPI并行的加速比Fig.6 Speed-up between G-FastICA and serial or MPI 本文研究了高光谱影像降维快速独立成分分析方法,提出和实现了基于GPU的G-FastICA并行算法,并基于GPU架构对算法进行优化研究。实验结果显示了GPU比CPU具有更好的计算优势,G-FastICA并行算法最高可加速72倍。 通过在CPU/GPU异构系统上研究快速独立成分分析降维方法,获得了良好的性能,探讨了GPU加速高光谱影像降维的可行性,切实加速了高光谱影像降维过程。本文算法可进一步扩展至GPU集群来提高性能。 References) [1]GreenRO,EastwoodML,SartureCM,etal.Imagingspectroscopyandtheairbornevisible/infraredimagingspectrometer(AVIRIS)[J].RemoteSensingEnviron, 1998, 65(3): 227-248. [2]GreenAA,BermanM,SwitzerP,etal.Atransformationfororderingmultispectraldataintermsofimagequalitywithimplicationsfornoiseremoval[J].IEEETransactiononGeoscienceandRemoteSensing, 2000, 26(1): 65-74. [3]KaarnaA,ZemcikP,KälviäinenH,etal.Compressionofmultispectralremotesensingimagesusingclusteringandspectralreduction[J].IEEETransactiononScienceRemoteSensing, 2000, 38(2): 1073-1082. [4]ScottD,ThompsonJ.Probabilitydensityestimationinhigherdimensions[C]//Proceedingsofthe15thSymposiumontheInterfaceComputerScienceandStatistics, 1983: 173-179. [5]JolliffeIT.Principalcomponnentanalvsis[M].USA:Sprinner-Verlan, 1986. [6]HyvärinenA,OjaE.Independentcomponentanalysis:algorithmandapplications[J].NeuralNetworks, 2000, 13(4-5): 411-430. [7]TenenbaumJB,DeSilvaV,LangfordJC.Aglobalgeometricframeworkfornonlineardimensionalityreduction[J].Science, 2000, 290(5500): 2319-2323. [8]RoweisST,SaulLK.Nonlineardimensionalityreductionbylocallylinearembedding[J].Science, 2000, 290(5500): 2323-2326. [9]TOP500.TOP500supercomputersites[EB/OL]. (2012-11) [2014-09-26]http://www.top500.org. [10]ValenciaD,LastovetskyA,O′FlynnM,etal.ParallelprocessingofremotelysensedhyperspectralimagesonheterogeneousnetworksofworkstationsusingheteroMPI[J].InternationalJournalofHighPerformanceComputingApplications, 2008, 22(4): 386-407. [11]PlazaJ,PlazaA,PérezR,etal.Parallelclassificationofhyperspectralimagesusingneuralnetworks[J].ComputationalIntelligenceforRemoteSensingStudiesinComputationalIntelligence, 2008, 133: 193-216. [12]SánchezS,RamalhoR,SousaL,etal.Real-timeimplementationofremotelysensedhyperspectralimageunmixingonGPUs[J].JournalofReal-timeImageProcessing, 2012, 32(1): 518-522. [13]YangH,DuQ,ChenGS.Unsupervisedhyperspectralbandselectionusinggraphicsprocessingunits[J].IEEEJournalofSelectedTopicsinAppliedEarthObservationsandRemoteSensing, 2011, 4(3): 660-668. [14]RamalhoR,TomásP,SousaL.EfficientindependentcomponentanalysisonaGPU[C]//Proceedingofthe10thIEEEInternationalConferenceonComputerandInformationTechnology,2010:1128-1133. [15]ForgetteJ,Wachowiak-SmolíkováR,WachowiakM.Implementingindependentcomponentanalysisingeneral-purposeGPUarchitectures[C]//ProceedingsoftheInternationalConferenceonDigitalInformationProcessingandCommunications2011:233-243. [16]HyvrinenA.Fastandrobustfixed-pointalgorithmsforindependentcomponentanalysis[J].IEEETransactionsonNeuralNetworks,1999,10(3):626-634. [17]HyvrinenA.Thefixed-pointalgorithmandmaximumlikelihoodestimationforindependentcomponentanalysis[J].NeuralProcessLett,1999,10(1):1-5. A parallel algorithm of FastICA dimensionality reduction for hyperspectral image on GPU FANG Minquan, ZHOU Haifang, ZHANG Weimin, SHEN Xiaolong Fastindependentcomponentanalysisdimensionalityreductionforhyperspectralimageneedsalargeamountofmatrixanditerativecomputation.Byanalyzinghotspotsofthefastindependentcomponentanalysisalgorithm,suchascovariancematrixcalculation,whiteprocessing,ICAiterationandICtransformation,aGPU-orientedmappingschemeandtheoptimizationstrategybasedonGPU-orientedalgorithmonmemoryaccessingandcomputation-communicationoverlappingwereproposed.Theperformanceimpactofthread-blocksizewasalsoinvestigated.Experimentalresultsshowthatbetterperformancewasobtainedwhendealingwiththehyperspectralimagedimensionalityreductionproblem:theGPU-orientedfastindependentcomponentanalysisalgorithmcanreachaspeedupof72timesthanthesequentialcodeonCPU,anditruns4~6.5timesfasterthanthecasewhenusinga16-coreCPU. graphicprocessingunit;hyperspectralimagedimensionalityreduction;fastindependentcomponentanalysis;parallelalgorithm;performanceoptimization 2014-09-28 国家自然科学基金资助项目(61272146,41375113,41305101) 方民权(1989—),男,浙江东阳人,博士研究生,E-mail:fmq@hpc6.com;周海芳(通信作者),女,教授,博士,硕士生导师,E-mail:haifang_zhou@163.net 10.11887/j.cn.201504011 http://journal.nudt.edu.cn TP A


2 FastICA算法并行化研究



3 GPU性能优化


4 实验结果





5 结论
