运用粒子群优化算法的平流层飞艇总体设计*

刘多能，杨希祥，麻震宇，侯中喜

运用粒子群优化算法的平流层飞艇总体设计*

刘多能，杨希祥，麻震宇，侯中喜

(国防科技大学 航天科学与工程学院， 湖南 长沙 410073)

平流层飞艇总重最小化能一定程度上反映总费用最低的设计目标，满足有效载荷功率需求是飞艇总体设计的出发点和落脚点。在飞艇参数建模中引入太阳电池曲面铺装模型以及昼夜能源闭环模型；以整艇重量最小为设计目标，以昼夜能源供需平衡、浮重平衡、推阻平衡三大平衡问题为约束条件，运用粒子群优化算法对飞艇的外形尺寸参数进行优化设计；分析了有效载荷功率需求和功率密度对于飞艇总体设计结果的敏感性。分析结果表明：飞艇总重随有效载荷功率线性增加；飞艇总重随有效载荷功率密度增加而迅速减小，但变化率逐渐变小，飞艇总重趋于稳定。能源系统仿真的结果表明了飞艇总体设计方法的有效性和设计结果的临界特性。

平流层飞艇；总体设计；粒子群优化算法

(CollegeofAerospaceSciencesandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China)

平流层飞艇依靠浮力驻空，可在长久定点驻空，时间可达数月甚至数年[1]。相对于航空器，平流层飞艇具有驻空时间长、覆盖区域广、控制范围大、生存能力强等特点，能够获得持久连续的战场侦察与监视效果；相对航天器，平流层飞艇距离地面近，具有较高的空间分辨率和时间分辨率，在对地观测和通信等领域具有优势[2]。

平流层飞艇通常采用太阳电池和储能电池的联合供电能源系统，太阳电池一般采用柔性薄膜太阳电池，储能电池一般采用锂电池或可再生燃料电池。太阳电池白天吸收太阳辐照，用于有效载荷、航电系统和推进系统能源消耗，剩余能量向储能电池充电；晚上储能电池放电，为飞艇各耗电系统供电。为实现飞艇在平流层长时间驻空，就必须解决昼夜能源供需平衡、浮重平衡、推阻平衡三大平衡问题。在飞艇设计之初，必须在总体层次根据任务需求与能耗水平权衡飞艇外形尺寸、太阳电池与储能电池的合理配置。

姚伟等以总重量最小为设计目标，给出了平流层飞艇总体参数估算方法，并针对季节、纬度、环境和关键技术参数进行了敏感性分析[3]。杨燕初等基于遗传算法，以能量平衡和系统总重最小为设计目标开展了飞艇外形优化设计方法研究[4]。Liang等设计了基于并行子空间的平流层飞艇总体参数多学科优化设计框架[5]。

1 飞艇参数模型

1.1 外形几何参数模型

图1 飞艇几何参数化描述Fig.1 Geometric parameters of an airship

飞艇外形参数化方程可表示为：

(1)

飞艇体积和表面积可通过式(2)和式(3)[3]近似计算：

(2)

Sas=2π(a1+a2)b=πld

(3)

式中，a1，a2为两个半椭球的长半轴长，b为两个半椭球的短半轴长，l和d分别为飞艇艇长和最大直径。飞艇长细比定义为：

(4)

1.2 阻力与推力模型

飞艇的阻力大部分由艇身产生，艇体阻力系数Cd可用式(5)进行估算[3]:

Cd=[0.172f1/30.252f-1.21.032f-2.7]/Re1/6

(5)

式中，Re为雷诺数。

考虑尾翼等阻力特性，通过修正得到整艇阻力系数为:

CD=Cd/0.5243

(6)

进而得到平流层飞艇所受阻力：

(7)

式中，ρa为所在高度大气密度，Uas为飞艇相对于大气的运动速度，针对定点驻留问题，Uas与风速大小相等。

平流层飞艇为实现定点驻留，需通过螺旋桨推进系统克服由于空速造成的阻力，所需推进系统功率和质量分别为：

Pthrust=FdragUas/ηthrust

(8)

mthrust=Pthrust/ρthrust

(9)

式中，ηthrust为推进系统效率(螺旋桨效率、电机效率、减速器效率的综合)，ρthrust为推进系统功率密度。

1.3 功率需求与能源系统模型

.3.1 太阳的空间位置

图2给出了太阳在地平坐标系中的位置。

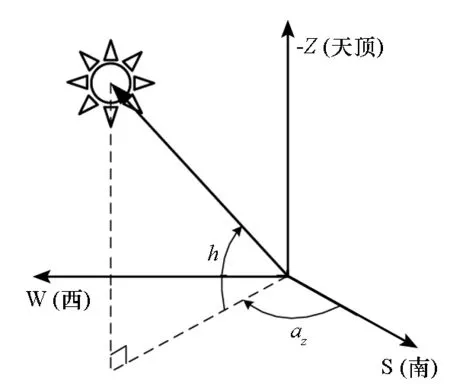
图2 太阳的空间位置Fig.2 Spatial location of the sun

图2中h为太阳高度角，在地平线上方为正；az为太阳方位角，正南方为0°，偏西为正。太阳在地平坐标系(北东地)的空间位置向量可用h和az这两个欧拉角来描述：

Sg=[-coshcosaz,-coshsinaz,-sinh]T

(10)

式中，h与az可利用式(11)、式(12)计算求得[6]。

h=arcsin(sinδsinλ+cosδcosωcosλ)

(11)

(12)

式中，δ，ω分别为太阳赤纬角和当地的真太阳时角[7]。

(13)

ω=(Hs+ΔTL+e-12)×15

(14)

式中：nd为从当年1月1日算起的日期序号；时角ω正午的时候为0°，0点到正午为正，正午到24点为负；Hs为当地的标准时间(钟表时间)；ΔTL与e代表两种不同的时差。太阳的方位与时角密切相关，在实际的辐照计算中需要考虑时差的影响。两种时差分别阐述如下[7]：

①当地经度与标准时间所在的经度之差造成的真太阳时差：

(15)

式中，时差单位是h，L是当地经度，Ls是标准时间经度，东经取正，西经取负，单位是(°)，例如北京时间所在经度是120°。

②真太阳时与平均太阳时的差：平均太阳时为当地标准时间；真太阳时是以太阳位于当地正南方的瞬时为正午，地球自转15°为1h，但由于太阳与地球间的距离和相对位置随时间在变化，以及地球赤道与其绕太阳运行轨道所处平面的不一致，从而出现时差。精确计算公式为：

(16)

式中，时差单位是h，Γ=2(nd-1)π/360。

.3.2 太阳直接辐照强度

太阳直接辐照强度是指，在垂直于阳光射线的表面上，单位时间内投射到单位面积上的太阳直接辐射能量[8]：

SI=SI0·E·τ

(17)

式中：SI0为太阳常数，取1367W/m2；E为日地距离修正系数；τ为大气透射率：

E=1+0.033cos(2πnd/365)

(18)

τ=0.56×(e-0.65m+e-0.095m)

(19)

式中，m为大气质量，表示大气对地球表面接收太阳光的影响程度，为无量纲量:

(20)

考虑气压的影响，大气质量应当表示为：

(21)

式中：P0为海平面的大气压；P(z)为高度为z处的大气压，由标准大气模型求得。

.3.3 太阳电池阵列曲面铺装模型

飞艇是轴对称的椭球体，采用平面假设[3]和圆柱假设[4]计算太阳能，误差较大，因此采用更加准确的曲面铺装模型。

因为太阳电池组件的面积远远小于飞艇表面积，可以假定飞艇上的每个组件是近似的平面。假定从飞艇截面半径最大处正上方分别沿圆周方向和纵轴(x轴)方向依次铺装太阳电池组件，并记录每一个组件的安装坐标(xi, αi)，如图3所示。图3中：Ri为组件所在飞艇纵向横截面圆的半径，可由组件的纵向位置坐标xi代入式(1)得到；αi为组件的安装角；Ni为组件表面的法向量，由母线在xoz平面的法向量Nz，绕x轴转动角度αi得到。在每个横截圆面圆周上对应的圆心角都应达到安装范围角θr。对铺排数量进行累加，计算太阳电池总面积，当该面积达到指定面积时停止铺排。

图3 太阳电池组件铺装示意图Fig.3 Sketch for paving solar modules

在飞艇总体设计中，太阳电池的铺装面积通常是一个设计参数，在能耗水平不变的条件下，能源供需平衡的面积临界值是定值。太阳电池面积作为一个内部搜索变量，给定一个面积值，就能通过上述铺装模型计算所有组件的铺装位置，进而计算全天的产能情况，如果这个面积值刚好能够满足后面1.3.6节中的能源供需平衡关系，这个值就作为参数设计的结果。

.3.4 太阳电池阵列实时输入功率计算模型

为了计算太阳电池阵列表面的有效太阳直接辐照(垂直于阵列表面的辐照)，首先将太阳方向向量转换到飞艇坐标系中：

Sa=TagSg

(22)

式中，Sa为飞艇坐标系中的太阳方向向量，Tag为地平坐标系到飞艇坐标系的坐标转换矩阵。

电池组件的入射辐射功率为直接辐照功率在组件表面的投影：

(23)

式中，si是组件面积。Ni·Sa≤ 0，表示太阳在当前组件所在切平面下方，组件表面处于背光面，辐射功率为0。

飞艇上某个时刻的太阳能输入总功率所有组件功率的累加和为：

(24)

式中，n为太阳电池组件数量，ηsolar为太阳电池转换效率。太阳电池的质量为：

msc=nScellρsc

(25)

式中，Scell为太阳电池组件面积，ρsc为太阳电池面密度。

.3.5 功率需求模型

有效载荷功率为：

Ppayload=mpayloadρpayload

(26)

式中，mpayload，ρpayload分别为有效载荷的质量及功率密度。

飞艇运行总功率为：

Ptotal=Ppayload+Pthrust+Pcontrol

(27)

式中，Pcontrol为控制系统(航电系统)、测量系统、数传系统等总功率。

.3.6 闭环能源系统模型

飞艇能源系统为负载供电的过程包含了太阳电池与储能电池联合供电的时间段，在清晨和傍晚太阳辐照较弱时均可达到小时量级。因而简单按照日出日落时间来分析能源供需平衡[5]会造成较大误差。采用基于时间推进的闭环能源系统模型。

(28)

式中，Qexc为一天当中太阳能满足整艇用电需求后的剩余太阳能，Qli为全天储能电池的供电电量，ηconvert为储能电池充、放电总效率。如果ε为一个极小的正数，则能源供需实现闭环，储能电池的质量也可确定为：

mli=Qli/(ηdeep·ρli)

(29)

式中，ηdeep为储能电池放电深度，ρli为储能电池能量密度。

1.4 浮力与总质量模型

飞艇所受总浮力为：

Fbuo=ρaVasg

(30)

式中，g为重力加速度。

假设在驻留段氦气充满，空气排空，驻留高度的氦气密度为ρHe，内外蒙皮平均面密度为ρenv，考虑实际加工过程引起蒙皮质量增加20%，则氦气的总质量与内外蒙皮总质量为：

mHe=ρHeVas

(31)

menv=1.2ρenvSas

(32)

根据尾翼面积与艇身体积的近似估算公式[5]，考虑实际加工过程引起蒙皮质量的增加，尾翼质量为：

mfin=1.2ρfin×0.012 1Vas

(33)

飞艇总质量为：

(34)

式中，mcontrol为控制系统质量，mstr为主结构(头锥、吊舱、连接片等)质量，可采用式(35)近似估算[5]：

mstr=0.25(menv+mfin+mthrust+msc+mli)

(35)

2 利用PSO算法求解飞艇参数优化问题

2.1优化问题确立

平流层飞艇的结构材料、能源系统造价昂贵，飞艇总重最小化能一定程度上反映总费用最低的设计目标。飞艇的总体设计优化可以表示为，以总重量为目标函数，以飞艇的外形参数a1和f为决策变量，以浮重平衡为约束条件的约束优化问题：

minJ=mtotal

w.r.ta1, f

s.t. mtotalg-Fbuo<0

其中，约束条件仅包含浮重平衡，而推阻平衡体现在式(8)推进系统的计算过程中，能源平衡体现在闭环能源系统模型中。当给定飞艇尺寸后，可根据式(28)确定匹配的太阳电池与储能电池配置。

2.2 粒子群优化算法

粒子群优化(ParticleSwarmOptimization，PSO)算法是由Kennedy等模仿鸟类觅食的过程设计的一种基于随机种群的全局优化技术[9]。PSO算法先是初始化一群随机粒子(潜在解)， 然后通过迭代更新, 比较适应度函数的大小来寻找最优解。每次迭代中, 粒子通过跟踪个体极值和全局极值来更新自己。PSO算法可以应用于约束优化问题的求解, 由于PSO算法的求解过程不依赖目标函数的解析性质, 可对解空间进行多点并行搜索, 很快PSO算法便发展成求解约束优化问题的有效算法之一[10]。而飞艇总体设计的流程具有非解析特性，并含有简单的约束条件，PSO算法可以解决该约束优化问题。

2.3 优化流程

飞艇外形优化的流程如图4所示，按照1.1～1.4节的顺序依次计算各个分系统的功耗、重量等参数，整个流程充分考虑了三大平衡约束。PSO算法根据每次迭代的总重结果与当前最小总重，更新有关外形尺寸(a1, f)的粒子群进入下一次迭代，直到收敛。

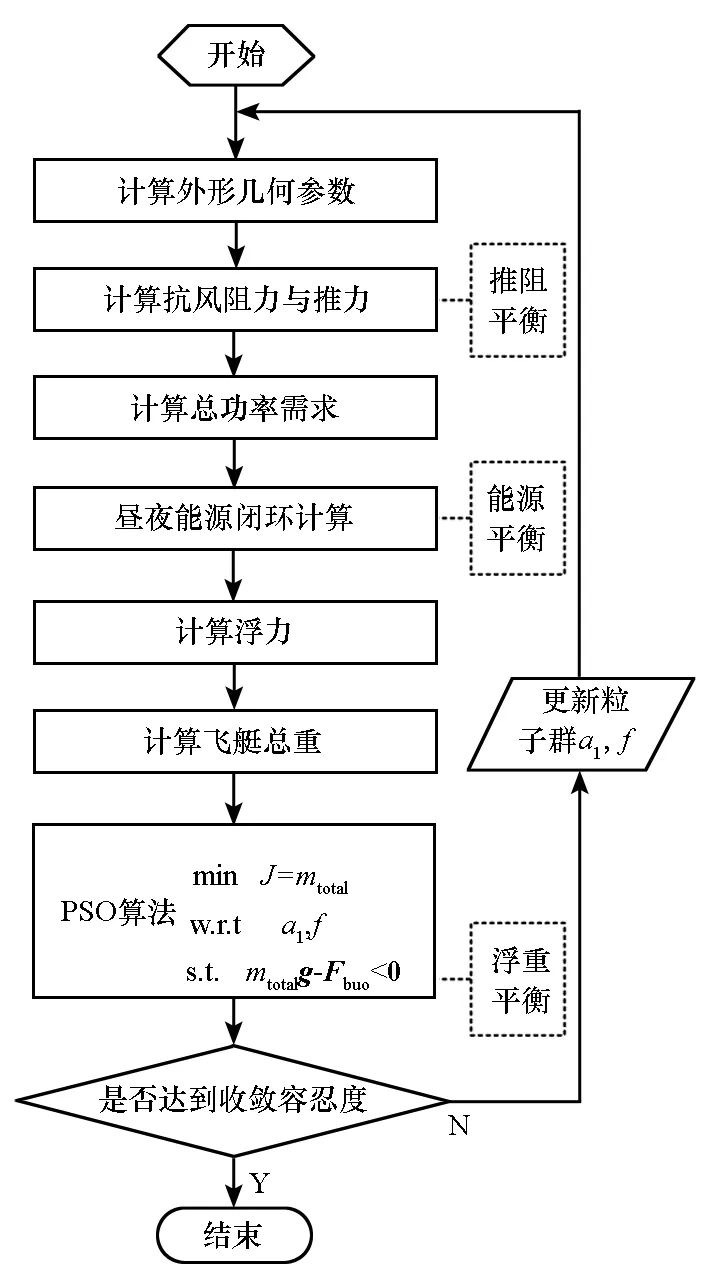
图4 飞艇外形优化的流程图Fig.4 Airship size optimization scheme

3 优化结果与分析

飞艇的总体优化设计应以满足任务需求为出发点和落脚点。定点驻留任务的需求包括的内容有时间段、地点(经纬度)、抗风能力、载荷水平等，假定当前飞艇的任务需求是在今年8月8日左右在北京附近(北纬40°，东经116°)，20kg高度进行长航时定点驻留飞行，当地的平均风速是15m/s。有效载荷功率需求是飞艇总体设计的原始驱动力，重点研究载荷功率和载荷功率密度对飞艇总体设计的影响。

首先考察不同载荷功率需求，对于飞艇总体设计的影响。假定当前的载荷功率密度水平为5.507W/kg(美国HAA方案)，有效载荷的重量随着功率需求的增加而增加。优化设计输入参数见表1，优化的结果如图5所示。

表1 总体优化设计输入参数

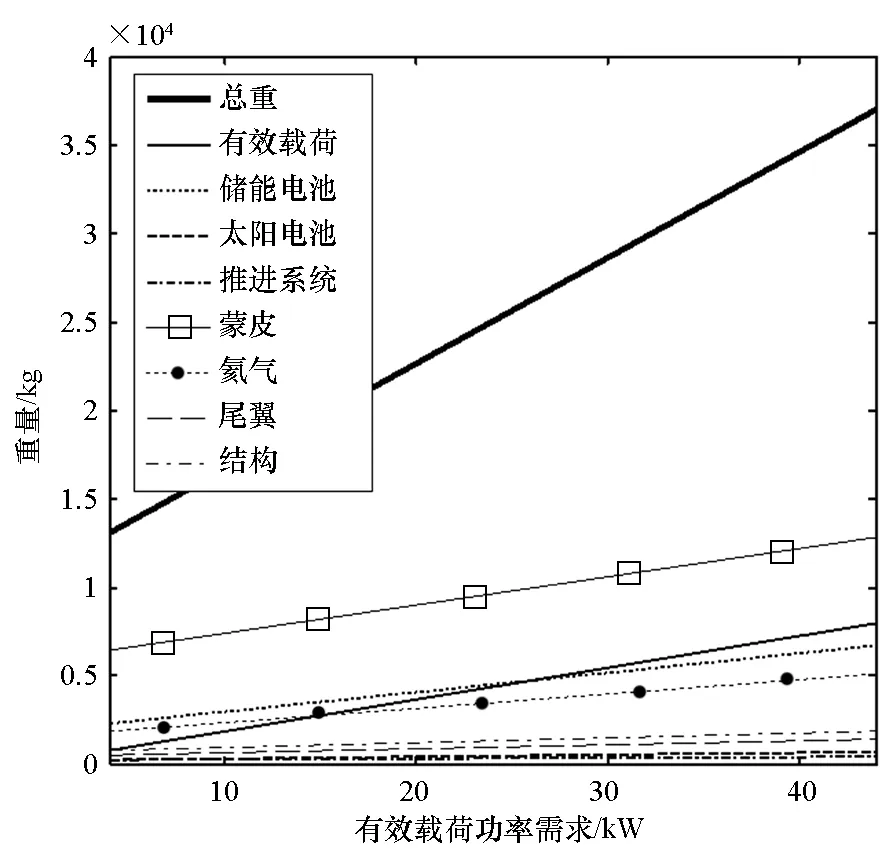
图5 飞艇重量组成随有效载荷功率变化关系Fig.5 Relationship between payload power requirement and weight of airship and its subsystems

从图5中可以看出有效载荷的功率需求和重量的增加，直接导致了飞艇总重量的增加，增加的比例远大于有效载荷自身重量的增加。一方面功率需求增加，可能需要更大的太阳电池铺装面积和储能电池重量，增加了飞艇总重，同时可能需要更大的飞艇表面积来铺装太阳电池，导致飞艇尺寸与重量的增大；另一方面有效载荷重量的增加导致原来的浮重平衡打破，需要增大飞艇尺寸来增加浮力，导致总重增加。

图6显示了太阳电池的铺装面积随有效载荷功率的变化关系，虚线表示飞艇上表面的可铺装面区域面积，根据表1中的铺装范围角θr= 90°可推算可铺装面积为飞艇表面积的1/4。

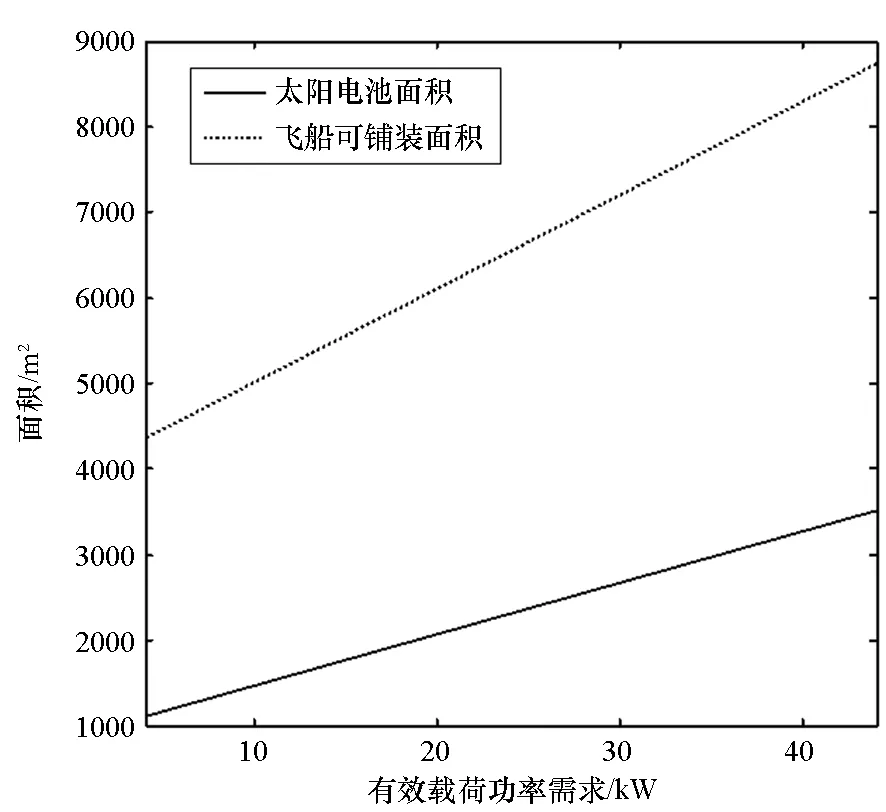
图6 太阳电池铺装面积随有效载荷功率变化关系Fig.6 Relationship between payload power requirement and area of solar cells

不同有效载荷功率条件下，太阳电池面积的需求远小于可铺装面积，可见有效载荷功率的增加并没有直接造成飞艇尺寸的增大。图5中飞艇总重的增加主要是由于有效载荷自身重量的增加，以及功率需求增加造成的储能电池重量增加。为了维持浮重平衡，飞艇体积增大，氦气质量随体积增大，蒙皮重量随表面积增加，同时阻力增加引起推进系统重量增加，进一步增加总重。而浮力与体积成正比，氦气密度比空气小得多，蒙皮重量、推进系统重量与体积的2/3次方成正比(见式(3)、(7)、(32))，总能找到浮重平衡点。以上分析说明浮重平衡约束相比能源平衡约束对于有效载荷功率的变化更加敏感。

有效载荷的功率需求不断增大，显著增加了飞艇制造成本。随着载荷技术向着小而精的方向发展，有效载荷的功率密度不断增加，在载荷技术上的局部投入增加是否有助于降低飞艇整体的质量水平值得研究。在功率需求一定(20kW)的条件下，改进有效载荷功率密度对于飞艇总体设计目标的影响如图7所示。

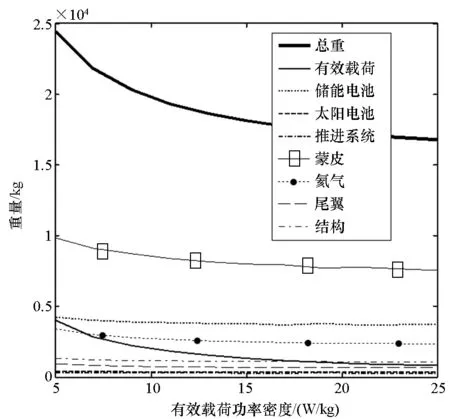
图7 飞艇重量组成随有效载荷功率密度变化关系Fig.7 Relationship between specify power of payload and weight of airship and its subsystems

从图7中可以看出，飞艇总重随着有效载荷功率密度的增加迅速减小，但变化率逐渐变小。这是因为功率不变的情况下，有效载荷重量与功率密度呈倒数关系，能源系统的配置基本保持不变，而飞艇总重的减小基本由有效载荷自身重量减小造成。随着有效载荷功率密度的进一步增大，相比飞艇总重，有效载荷重量变得非常小，飞艇的重量分配基本保持平衡。这说明适当增加有效载荷功率密度可以降低飞艇总重，但当有效载荷重量占比较小时，功率密度增加对于优化目标贡献较小。

4 仿真验证

图8 能源系统仿真结果Fig.8 Simulation results for energy system

总体设计后得到的飞艇参数包括飞艇的外形尺寸、太阳电池、储能电池的配置以及功耗水平。由于飞艇上能量的转换、存储与消耗是一个随时间推进而变化的复杂过程，通过飞艇能源系统的仿真，模拟太阳能、二次能源与实时能耗之间的动态关系，考察其昼夜能源闭环能力是分析和评估飞艇总体设计参数的有效手段。针对第3节当中提到的任务需求，利用文献[11]中的能源系统仿真与续航时间评估平台对其中一组总体设计结果(ρpayload= 25W/kg，Ppayload=20kW)进行仿真验证，结果如图8所示。图8中粗黑实线代表太阳电池输出总功率Psolar，当Psolar>0时，代表白天，当Psolar=0时，代表黑夜。

飞艇能够持续工作4d以上，在任意24h内，昼夜能量供需基本平衡。但是随着日期向后推移，白天日照时间略有减少，夜间时间相对增加，从图8中可以看出白天太阳电池输出总功率呈下降趋势，夜间储能电池消耗的电量有上升趋势，导致最后一天白天储能电池出现不能充满的情况，在夜间放电触及放电深度，导致续航结束。

仿真结果一方面表明总体设计结果能够满足任务需求，特别是在总体设计输入的日期和地点上；另一方面总体设计的结果只能给出一种处于临界状态的设计参考，并不能针对所有的情形给出一个通用设计方案。因而在飞艇设计之初，要重点考虑任务周期内最低辐照的情形，对飞艇参数进行最优配置，在实际应用中应在参考总体设计结果的基础上进行冗余设计。

5 结论

1)在有效载荷功率密度一定的条件下，飞艇总重随有效载荷功率线性增加；浮重平衡约束相比能源平衡约束对于有效载荷功率的变化更加敏感。

2)在有效载荷功率需求一定的条件下，飞艇总重随着有效载荷功率密度的增加迅速减小，但变化率逐渐变小，飞艇总重趋于稳定；当功率密度较大时， 有效载荷功率密度不再是飞艇总体设计的重要影响因素。

3)总体设计的结果一种临界设计方案，实际应用中应在参考总体设计结果的基础上进行冗余设计。

References)

[1] 王彦广，李健全，李勇,等. 近空间飞行器的特点及其应用前景[J]. 航天器工程，2007，16(1):50-57.

WANGYanguang,LIJianquan,LIYong,etal.Charactersandapplicationprospectsofnearspaceflyingvehicles[J].SpacecraftEngineering, 2007, 16(1):50-57. (inChinese)

[2] 沈海军，程凯，杨莉. 近空间飞行器[M]. 北京: 航空工业出版社, 2012.SHENHaijun,CHENGKai,YANGLi.Nearspaceaerocraft[M].Beijing:AviationIndustryPress, 2012. (inChinese)

[3] 姚伟，李勇，王文隽,等. 平流层飞艇优化方法和设计参数敏感性分析[J]. 宇航学报, 2007, 28(6): 1524-1528.

YAOWei,LIYong,WANGWenjun,etal.Stratosphericairshipoptimizationmethodanddesignparameterssensitivityanalysis[J].JournalofAstronautics, 2007, 28(6): 1524-1528.(inChinese)

[4] 杨燕初，王生，顾逸东,等. 基于遗传算法的临近空间飞艇多学科优化设计[J]. 计算机仿真, 2012, 29(4): 49-54.

YANGYanchu,WANGSheng,GUYidong,etal.Multidisciplinarydesignoptimizationofnearspaceairshipbasedongeneticalgorithm[J].ComputerSimulation, 2012, 29(4): 49-54.(inChinese)

[5]LiangHQ,ZhuM,GuoX,etal.Conceptualdesignoptimizationofhighaltitudeairshipinconcurrentsubspaceoptimization[C]//Proceedingsof50thAIAAAerospaceSciencesMeetingincludingtheNewHorizonsForumandAerospaceExposition,AIAA2012-1180, 2012.

[6] 郑威，宋琦，李勇,等. 平流层飞艇太阳电池阵发电功率计算及分析[J]. 宇航学报, 2010, 31(4): 1224-1230.

ZHENGWei,SONGQi,LIYong,etal.Computationandanalysisofpowergeneratedbythesolarcellarrayofastratosphericairship[J].JournalofAstronautics, 2010, 31(4): 1224-1230.(inChinese)

[7]RanHJ,ThomasR,MavrisD.Acomprehensiveglobalmodelofbroadbanddirectsolarradiationforsolarcellsimulation[C]//Proceedingsof45thAIAAAerospaceSciencesMeetingandExhibit,AIAA2007-33, 2007.

[8]KreithF,KreiderJF.Numericalpredictionoftheperformanceofhighaltitudeballoons[R].Boulder,Colorado:AtmosphericTechnologyDivision,NationalCenterforAtmosphericResearch, 1971.

[9]KennedyJ,EberhartRC.Particleswarmoptimization[C]//ProceedingsofIEEEInternationalConferenceonNeuralNetworks, 1995.

[10] 高显忠，罗文彩，侯中喜. 应用改进PSO算法求解待约束优化问题[J]. 计算机仿真， 2009, 26(10): 212-215.

GAOXianzhong,LUOWencai,HOUZhongxi.ApplicationofanimprovedPSOalgorithminsolvingconstrainedoptimizationproblem[J].ComputerSimulation, 2009, 26(10): 212-215.(inChinese)

[11] 刘多能，杨希祥，侯中喜,等. 平流层飞艇能源系统仿真与续航时间估算[C]. 第三届高分辨率对地观测学术年会临近空间对地观测技术分会， 湖南，长沙，2014.

LIUDuoneng,YANGXixiang,HOUZhongxi,etal.Energysystemsimulationandenduranceestimationforstratosphereairship[C].The3rdChinaHighResolutionEarthObservationConference(BranchConferenceonNearspace),Changsha,Hunan, 2014.(inChinese)

Conceptual design of stratospheric airship based on particle swarm optimization algorithm

LIU Duoneng, YANG Xixiang, MA Zhenyu, HOU Zhongxi

Minimizingthetotalweightofastratosphericairshipreflectsthedesignobjectoflowesttotalcosttoacertainextent.Tomeetthepowerrequirementofpayloadisthespringboardandgoalfortheconceptualdesignoftheairship.Themodelofpavingsolarcellsoncurvedsurfaceandthemodelofenergy-closedloopduringdayandnightwereintroducedintheparametricmodelingoftheairship.Theparticleswarmoptimizationalgorithmwasusedtooptimizetheparametersoftheoutsidesize.Thedesignobjectistofindafeasibleairshipwhichhasminimumtotalmassandsatisfiestheconstraintswiththreebalances:thediurnalbalancebetweentheenergysupplyandtheenergyrequirement,thebalancebetweenmassandbuoyancy,andthebalancebetweendragandthrust.Thesensitivityoftheoptimizationresultswithdifferentrequirementofpayloadpowerandpayloadspecificpowerwasanalyzed.Theanalysisresultsshowthat:thetotalairshipweightincreaseslinearlywiththepayloadpower;thetotalairshipweightdecreasessteeplywiththepayloadpowerdensity,butthechangerateofthetotalweightalsodecreasesandthetotalweighttendstobestable.Theresultsofenergysystemsimulationindicatethevalidityoftheconceptualdesignmethod,aswellasthecriticalcharacteristicsofthedesignresults.

stratosphericairship;conceptualdesign;particleswarmoptimizationalgorithm

2015-04-18

国家高分重大专项资助项目(GFZX04060103)

刘多能(1986—)，男， 湖南双峰人，博士研究生，E-mail：liuduoneng@nudt.edu.cn；杨希祥(通信作者)，男，副教授，博士，硕士生导师，E-mail：nkyangxixiang@163.com

10.11887/j.cn.201504009

http://journal.nudt.edu.cn

TK

A