应用极化聚类中心设计快速自适应极化滤波器*

任 博，罗笑冰，邓方刚，王国玉

(1. 国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室， 湖南 长沙 410073；

2. 国防科技大学 电子科学与工程学院， 湖南 长沙 410073； 3.武汉军事代表局， 湖北 武汉 430077 )

应用极化聚类中心设计快速自适应极化滤波器*

任 博1,2，罗笑冰2，邓方刚3，王国玉1

(1. 国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室， 湖南 长沙 410073；

2. 国防科技大学 电子科学与工程学院， 湖南 长沙 410073； 3.武汉军事代表局， 湖北 武汉 430077 )

针对传统自适应极化滤波算法存在收敛速度慢、迭代步长因子选取困难等问题，采用极化聚类中心估计理论设计了一种快速自适应极化滤波器，实现了对极化雷达回波中的干扰信号逐脉冲地自适应精确对消。滤波器通过距离单元选通获取干扰信号样本，对样本极化聚类中心的直接计算能够快速估计干扰信号在当前脉冲内极化状态，依据干扰输出功率最小原则最终实现快速滤波过程，相比于传统极化滤波算法有更快的收敛速度和更稳定的干扰抑制性能。仿真对比实验结果验证了该方法的快速有效性。

极化自适应滤波；极化聚类中心；脉内滤波

(1.StateKeyLaboratoryofComplexElectromagneticEnvironmentEffectsonElectronics&InformationSystem,Changsha410073,China;

2.CollegeofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China;

3.WuhanMilitaryRepresentativeBureau,Wuhan430077,China)

随着现代电子战的迅猛发展，为适应日益复杂而恶劣的电磁环境，提高雷达战场生存和抗干扰能力，国内外研究者对雷达极化信号处理技术给予了高度关注。极化滤波技术已被证明是除时频空域滤波外又一种有效的干扰抑制技术途径[1]，至今已先后发展出多种极化滤波器，按照设计思想可以归纳为三类[2]：一是基于目标极化匹配接收思想，在目标极化先验已知或可估计的情况下，通过使接收天线极化与目标极化相匹配，从而提高信号与干扰噪声功率比(SignaltoInterferenceandNoiseRatio,SINR)，基于该思想的滤波器主要包括零相移极化滤波[3-5]、基于斜投影的极化滤波器[6-7]等。二是通过SINR输出最优化设计，综合考虑天线波束内目标及干扰极化，通过调整接收极化使信号干扰功率比或信号干扰功率差[8]等指标达到最优，典型代表是最优自适应极化滤波器[9-10]。上述两类滤波算法均依赖于目标极化的先验信息，然而在实际对抗环境中，特别是有源压制干扰条件下，目标回波通常会被干扰信号“淹没”，造成目标极化特性无法预先估计。第三类滤波器是采用发射与接收极化分别优化，通过接收变极化最大程度抑制干扰的同时，调整发射极化使目标回波增强[11]。由于接收极化的自适应只需估计干扰极化信息，此类极化滤波器更适用于实际工程应用，现有的干扰抑制滤波器主要包括自适应极化对消器(AdaptivePolarizationCancellers,APC)[12]、MLP-APC多凹口逻辑积自适应极化对消器(MultinotchLogic-productAdaptivePolarizationCancellers,MLP-APC)[13]以及多凹口逻辑乘次优自适应极化对消器(MultinotchLogic-productSuboptimumAdaptivePolarizationCancellers,MLP-SAPC)[14]等。然而相比传统APC，MLP方法由于采用非线性处理，使得信号相参性遭到破坏，因此受到应用场合的限制。相对而言，传统APC滤波器能够自动补偿通道间的幅相不均衡，对于极化固定或缓变的杂波、干扰都具有较好的抑制性能，在工程上得到广泛应用，但是在实际应用过程中仍然发现其存在一些问题。

现有的APC算法是基于负反馈思想，利用最陡梯度方法获取最优滤波权值[15]，进而通过加权求和实现干扰对消，其通道最优权值需经过迭代计算获取，收敛过程受到迭代步长因子取值的影响严重。本文将首先建立有源干扰条件下雷达接收目标回波的极化观测模型，在此基础上给出新的快速自适应极化滤波器的设计流程和滤波原理，最后对滤波器的性能开展对比仿真实验。

1 极化接收信号模型

考虑极化雷达系统具有水平和垂直正交双极化接收能力，且水平、垂直通道能够同时采集到天线的电磁波。假设每个发射脉冲后的时域接收采样点数为N，其具体数值由接收机采样率和采样时长决定，接收机收到的第n个采样点的信号可以表示为一个二维复矢量x(n)=[xH(n)xV(n)]T，其中xH(n)与xV(n)分别为水平和垂直通道在该点的复包络，其中包含目标后向散射回波s(n)=[sH(n)sV(n)]T、干扰信号i(n)=[iH(n)iV(n)]T以及通道热噪声q(n)=[qH(n)qV(n)]T，可得雷达回波观测矢量如式(1)所示。

x(n)=s(n)+i(n)+q(n) (n=1,2, …, N)

(1)

由于满足远场条件，式(1)可看作平面电磁波在一组正交基下的Jones矢量表征，根据电磁波瞬态极化理论，可以给出该电磁波的时域瞬时极化相干矢量[16]。

c(n)=x(n)⊗x*(n) (n=1, 2, …, N)

(2)

式中，⊗表示Kronecker积，*表示复数共轭，在此基础上可获得其时域瞬态Stokes矢量，记为j(n)。

j(n)=Rc(n)=[g0(n),gT(n)]T

(3)

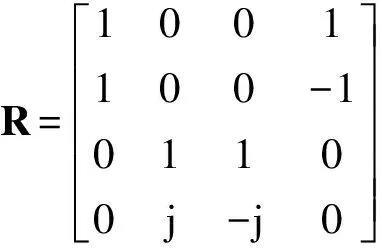
(4)

2 快速自适应极化滤波器设计

传统APC算法的本质是利用正交极化通道信号的互相关性自动地调整两通道的加权系数，最终使接收极化与干扰极化互为正交极化，从而抑制干扰。该算法基本处理流程主要分成两步：首先令主极化和辅助极化通道只接收干扰信号，再利用“最陡梯度”的思想通过迭代计算通道间的最优加权系数，该系数能够保证通道加权后输出的干扰功率最小；之后在干扰和目标同时存在的情形下，利用计算出的权系数对两极化通道加权求和实现干扰对消。然而在实际应用中发现，一方面算法中的迭代因子往往难以自适应选取，而该迭代算法的收敛速度和性能却直接受到该因子选取的影响[17]；另一方面在迭代步长因子确定后，为获得最优加权值，APC需要保证足够长的迭代时间，这会严重影响雷达信号处理的时效性。

图1 快速自适应极化滤波器处理流程图Fig.1 Process flow chart of the FAPF

针对上述问题，本文应用极化聚类中心思想设计了一种快速自适应极化滤波器(FastAdaptivePolarizationFilter，FAPF)，该滤波器的处理流程如图1所示。首先选取单个脉冲回波中干扰信号较纯净的部分，即每个脉冲重复周期内末尾一段的信号采样进行距离单元选通，如图1中颜色较深的距离单元；然后通过计算其时域极化聚类中心，从而估计干扰极化，再根据最优极化接收理论获取通道加权系数；最后对整段回波通道加权后输出滤波结果。利用数字信号处理的方法能够实现单个脉冲内极化捷变，不仅能够随干扰极化状态的改变而自适应调整接收极化抑制干扰，且无须考虑迭代步长因子选取问题，下面给出FAPF方法的滤波原理。

2.1 干扰信号极化状态估计

(5)

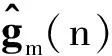
(6)

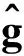
(7)

用于估计干扰极化状态的样本数K，会影响干扰极化聚类中心的估计精度，进而影响极化滤波器的干扰抑制性能。文献[18]研究表明在复高斯假设下，电磁波极化估计值的概率密度函数与电磁波真实的极化度以及估计样本数有关，并且对样本极化估计值的置信区间可通过样本数K加以控制，一般来讲在干扰源状态不变的情况下，即电磁波真实极化度固定，样本数越大，极化估计值的置信区间越窄，其估计的精度也就越高。然而由于采用脉内极化滤波方式，用于估计干扰信号距离段无法探测目标，样本数越大雷达在采用该种抗干扰模式下可探测目标的距离就会相应缩短，因此在实际工程中应折中考虑极化估计精度和所能承受的雷达威力的损失。本文的第3节将进一步结合仿真实验说明样本数选取对于滤波性能的影响。

2.2 最优接收极化滤波

(8)

(9)

根据矩阵理论可以得出接收天线最佳极化Stokes子矢量gro为

(10)

通过水平、垂直极化基下的极化比与Stokes矢量之间的转换关系，得到用于对V通道加权的最优权值如式(11)所示。

(11)

利用该权值对双通道接收到的全部距离段信号作归一化加权处理，得到最终滤波输出结果为

(12)

FAPF方法对干扰极化估计所需样本量更少，耗时更短，更易于实现逐个脉冲内的极化滤波。这是源于FAPF方法是通过对样本直接计算干扰极化聚类中心估计干扰极化，而普通APC方法则是对干扰样本执行顺序迭代计算直至权系数收敛，因此将能够有效节省样本数量和计算时间。此外，FAPF方法通过聚类中心的估计避免了APC方法迭代因子选取困难的问题，使得其滤波性能不受参数选取的影响而仅与干扰本身的极化纯度有关。

3 实验结果及性能分析

3.1 仿真实验

为模拟雷达在有源压制干扰环境下进行目标探测，设定仿真参数如表1所示。

表1 仿真参数设置

(a) 滤波前水平通道接收信号(a) Signals in horizontal channel without filtering

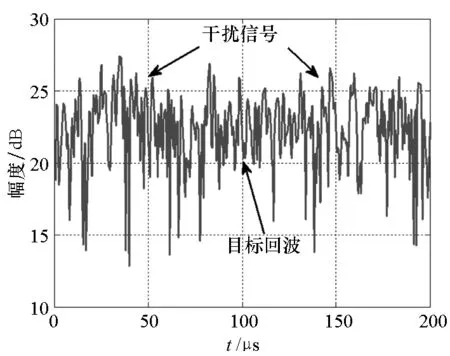
(b) 滤波前垂直通道信号(b) Signals in vertical channel without filtering

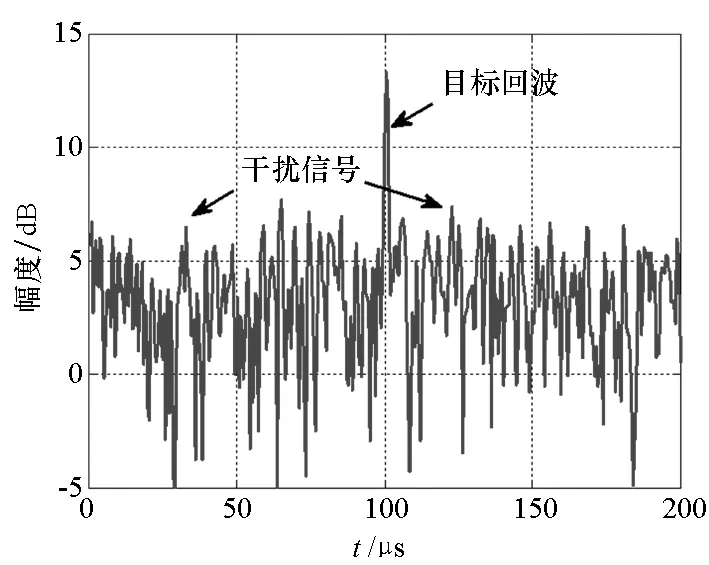
(c) FAPF滤波后输出信号(c) Output signals after FAPF filtering图2 极化滤波前后信号时域图Fig.2 Signals in time domain before and after polarization filtering

选取雷达频段为超高频(UltraHighFrequency,UHF)波段，发射非线性调频信号。为便于数字仿真，利用表1中仿真参数直接产生接收机处理后的视频信号，经匹配滤波处理后通过FAPF滤波器滤波，选取脉冲末尾的样本数为100，对应距离损耗约7.5km。图2给出了单个脉冲经FAPF滤波前后的仿真结果，从图2(a)、(b)中不难看出未经过极化滤波的水平和垂直通道中，即使经过脉压处理仍无法发现目标，而经快速极化滤波处理后，干扰信号得到抑制，目标回波得以显现，如图2(c)所示，经统计干扰信号功率降低约29dB。从而证明该算法能够在单个脉冲重复周期内完成对有源压制干扰的有效抑制。

3.2 滤波性能对比实验

(a)目标与干扰极化夹角对滤波器性能的影响(a) Effect of the polarization angle between target and jam on the filter performance

(b)不同干扰极化下滤波器干扰抑制性能(b) Performance of the interference suppression of the filter with different polarization state图3 极化滤波性能与目标干扰极化的关系Fig.3 Relationship between the performance of polarization filter and the polarizing state of the target interference

为衡量滤波器性能，在上节实验条件基础上给出了分别采用普通APC滤波器和FAPF滤波器滤波。图3(a)给出了两种滤波器输出信干噪比随目标干扰极化夹角的变化关系，利用Poincare极化球表征目标极化与干扰极化时，定义极化夹角为二者Stokes矢量点与球心构成的夹角。保持目标极化不变，改变干扰信号极化状态获得不同的极化夹角。

图3(a)所示目标与干扰极化越接近，极化角度差越小，无论是FAPF还是APC滤波器的滤波性能都会变差，这是因为目标与干扰的极化差异变小，因此在滤除干扰的同时对于目标的损耗也较大。然而FAPF方法比APC方法在信干噪比改善上约有1dB的提升，这主要是因为APC方法在迭代收敛过程中，受步长因子选取的影响，在有限样本条件下，权值未能收敛至最优值，因而存在对消剩余，而FAPF算法是对干扰信号极化聚类中心的最优估计，其估计精度只与干扰信号极化度有关，不存在迭代因子选取问题，能够达到干扰抑制的最佳性能。

将滤波前后干扰功率抑制比定义为Sr=Pin/Pout，其中Pin和Pout分别为滤波前后干扰信号功率。图3(b)给出了分别采用两种方法后干扰功率抑制比同干扰极化状态的关系曲面，这里干扰极化状态由极化相位描述子(γ,φ)表征，由图可见两种滤波方法均能够获得28.5dB以上的干扰抑制效果，综合两幅图来看在任意干扰极化状态下本文所提FAPF方法相比APC算法，滤波性能均有提升，特别是在干扰极化接近水平(γ=0°)或垂直极化(γ=90°)时，由于此时存在某一极化通道干扰信号的干噪比较低，利用APC方法时主通道的极化特性变差，受步长因子的影响，其对消剩余增大，而FAPF方法由于综合考虑两个通道总的极化特性，因而其抑制比受影响较小。

图4 极化滤波性能与权值计算时间的关系Fig.4 Relationship between the performance of the polarization filter and the computing time of the weight

固定干扰极化，图4给出了不同干扰噪声功率比(分别取20dB，40dB和60dB)条件下，滤波器收敛性能的对比，由图不难看出，随着干噪比的增大，干扰信号功率抑制比相应增加，这是由于干噪比越大使得混合接收信号极化度越高，对消性能就越好。一方面从权值计算过程来看，采用APC算法时，迭代获取最优权值的收敛时间在干噪比为20dB，40dB和60dB时分别需要75μs，150μs和250μs，并且随着干噪比的增大收敛所需的时间越长，然而FAPF算法则几乎不受权值计算时间的影响，30μs即可获得最优滤波效果，从滤波效率的角度，FAPF算法要优于传统APC算法。另一方面FAPF算法中权值计算时间与干扰估计样本数一一对应，从样本数选取的角度来讲，样本数大于60时，增大样本个数对于滤波器性能的改善影响较小，这说明此时已经满足干扰极化估计的精度要求。因此在工程中当干噪比大于20dB，只需使用60～100个样本点用于估计干扰极化。

4 结论

利用对干扰极化聚类中心的快速估计，取代了传统APC方法的顺序迭代计算过程，也避免了迭代因子难以自适应选取的问题，FAPF算法在有效抑制有源压制干扰的同时，缩短了滤波权系数计算时间，提高了滤波器抗干扰的稳定性。由于自适应极化滤波器的滤波性能不可避免地受到干扰信号特性、接收机通道特性以及环境特性等的影响，这是极化滤波技术进一步走向工程应用亟待开展的研究方向。

References)

[1]WangXS,XuZH,XiaoSP,etal.Performanceanalysisofadaptivepolarizationfilters[C]//ProceedingsofInternationalRadarConference,Adelaide:IEEE, 2003: 646-651.

[2]StaporDP.Optimalreceiveantennapolaizationinthepresenceofinterferenceandnoise[J].IEEETransactionsonAntennasandPropagation, 1995, 43(5): 473-477.

[3]DaiHY,WangXS,LuoJ,etal.Anewpolarimetricmethodofusingspatialpolarizationcharacteristicsofscanningantenna[J].IEEETransactionsonAntennasandPropagation, 2012, 60(3): 1653-1656.

[4]DaiHY,WangXS,LiYZ,etal.Main-lobejammingsuppressionmethodofusingspatialpolarizationcharacteristicsofantennas[J].IEEETransactionsonAerospaceandElectronicSystems, 2012, 48(3): 2167-2179.

[5] 戴幻尧, 李永祯, 刘勇, 等. 单极化雷达的空域零相移干扰抑制极化滤波器[J]. 系统工程与电子技术, 2011, 33(2): 290-295.

DAIHuanyao,LIYongzhen,LIUYong,etal.Spatialnullphase-shiftinterferencesuppressionpolarizationfilterdesignforsinglepolarizedradars[J].SystemsEngineeringandElectronics, 2011, 33(2): 290-295. (inChinese)

[6]MaoXP,LiuAJ,HouHJ,etal.Obliqueprojectionpolarisationfilteringforinterferencesuppressioninhigh-frequencysurfacewaveradar[J].IETRadarSonarNavigation, 2012, 6(2): 71-80.

[7]HongH,MaoXP,HuC.Amulti-domaincollaborativefilterforHFSWRbasedonobliqueprojection[C] //ProceedingsofIEEERadarConference,Atlanta,GA, 2012: 0907-0912.

[8] 王雪松, 汪连栋, 肖顺平, 等. 自适应极化滤波器的理论性能分析[J]. 电子学报, 2004, 32(4): 1326-1329.

WANGXuesong,WANGLiandong,XIAOShunping,etal.Theoreticalperformanceanalysisofadaptivepolarizationfilters[J].ActaElectronicaSinica, 2004, 32(4): 1326-1329. (inChinese)

[9]WangXS,ChangYL,DaiDH,etal.BandcharacteristicsofSINRpolarizationfilter[J].IEEETransactionsonAntennasPropagation, 2007, 55(4): 1148-1154.

[10]TianX.Novelpolarizationfilterdesignforwidebandradar[J].JournalofSystemsEngineeringandElectronics, 2012, 23(4): 522-528.

[11] 施龙飞, 王雪松, 肖顺平, 等. 干扰背景下雷达最佳极化的分步估计方法[J]. 自然科学进展, 2005, 15(11): 1324-1329.

SHILongfei,WANGXuesong,XIAOShunping,etal.Astepestimationmethodoftheradaroptimalpolarizationininterferencebackground[J].ProgressinNaturalScience, 2005, 15(11): 1324-1329. (inChinese)

[12]NathansonFE.Adaptivecircularpolarization[C]//ProceedingsofIEEEInternationalRadarConference,Arlington,VA, 1975: 221-225.

[13]GiuliD,FossiM,GheraadelliM.Atechniqueforadaptivepolarizationfilteringinradars[C]//ProceedingsofIEEEInternationalRadarConference,Arlington,VA, 1985: 213-219.

[14]GherardelliM.Adaptivepolarizationsuppressionofintentionalradardisturbance[J].IEEProceedingsofRadarandSignalProcessing, 1990, 137(6): 407-416.

[15] 施龙飞, 王雪松, 徐振海, 等.APC迭代滤波算法与性能分析[J]. 电子与信息学报, 2006, 28(9): 1560-1564.

SHILongfei,WANGXuesong,XUZhenhai,etal.Theiterative-filteringschemeanditsperformanceanalysisofAPC[J].JournalofElectronics&InformationTechnology, 2006, 28(9): 1560-1564. (inChinese)

[16] 王雪松. 宽带极化信息处理的研究[D]. 长沙：国防科学技术大学，1999.

WANGXuesong.Studyonwide-bandpolarizationinformationprocessing[D].Changsha:NationalUniversityofDefenseTechnology, 1999. (inChinese)

[17] 任博, 施龙飞, 王洪军, 等. 抑制雷达主波束内GSM干扰的极化滤波方法研究技术[J]. 电子与信息学报, 2014, 36(2): 459-464.

RENBo,SHILongfei,WANGHongjun,etal.InvestigationonpolarizationfilteringschemetosuppressGSMinterferenceinradarmainbeam[J].JournalofElectronics&InformationTechnology, 2014, 36(2): 459-464. (inChinese)

[18]MedkourT,WaldenAT.Statisticalpropertiesoftheestimateddegreeofpolarization[J].IEEETransactionsonSignalProcessing, 2008, 56(1): 408-414.

[19] 庄钊文，肖顺平，王雪松. 雷达极化信息处理及其应用[M]. 北京：国防工业出版社，1999：101-109.ZHUANGZhaowen,XIAOShunping,WANGXuesong.Radarpolarizationinformationprocessingandapplication[M].Beijing:DefenseIndustryPress, 1999: 101-109. (inChinese)

Design of fast adaptive polarization filters utilizing polarizing cluster center

REN Bo1,2, LUO Xiaobing2, DENG Fanggang3, WANG Guoyu1

Accordingtothetraditionaladaptivepolarizationfilteralgorithmshadproblemsoflowconvergencespeedandtheiterativefactorbeinghardtochoose,afastadaptivepolarizationfilterwasdesignedbyutilizingtheestimationtheoryofpolarizingclustercenter.Theinterferencesignalinpolarimetricradarreceptioncouldbecancelledaccuratelyandadaptivelypulse-by-pulse.Therange-gatedtechniquein-pulsewasadoptedtoobtaintheinterferencesignalsamples.Thecurrentpolarizationstateoftheinterferencesignalwasestimatedrapidlybycomputingthepolarizingclustercenterdirectly.Basedontheprincipalofminimuminterferenceoutputpower,thefastfilterprocesscouldbecarriedout.Comparedtothetraditionalpolarizationfilter,itisfasterinconvergenceandmorestabletotheperformanceofinterferencesuppression.Rapidityandefficiencyofthefilteralgorithmarevalidatedbysimulationresults.

polarizationadaptivefilter;polarizingclustercenter;filterin-pulse

2014-08-25

国家自然科学基金青年科学基金资助项目(41301490)

任博(1986—)，男，河北邯郸人，博士研究生，E-mail：rb410@139.com；王国玉(通信作者)，男，研究员，博士，博士生导师，E-mail：nudtgjs@gmail.com

10.11887/j.cn.201504015

http://journal.nudt.edu.cn

TN

A