二阶阶跃模型下导航信号畸变对接收机载噪比估计影响分析*

关刚强，庞 晶，刘文祥，王飞雪

(国防科技大学 电子科学与工程学院， 湖南 长沙 410073)

二阶阶跃模型下导航信号畸变对接收机载噪比估计影响分析*

关刚强，庞 晶，刘文祥，王飞雪

(国防科技大学 电子科学与工程学院， 湖南 长沙 410073)

载噪比作为评估导航信号质量的重要指标，直接影响着接收机的捕获、跟踪和电文解调性能。推导了基于国际民航组织二阶阶跃信号畸变模型下导航接收机采用相关、非相关处理时载噪比估计与畸变模型参数之间的解析表达式，并分析了畸变参数对导航接收机载噪比估计误差的影响。理论分析及仿真结果表明：数字畸变参数变化范围下导航信号载噪比变化在10-2量级，增大模拟畸变的振荡频率或者减小衰减频率将会提高载噪比估计值，模拟畸变参数变化引起的载噪比损耗可达0.1dBHz，畸变参数对载噪比估计的影响整体上都较小，因此导航接收机的载噪比输出不能作为监测导航信号是否异常的完备检测量。

载噪比估计；信号畸变；异常监测；二阶阶跃

(CollegeofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China)

目前，多数卫星导航接收机通过将接收信号与早、中、晚三个不同相位的本地伪码进行相关得到超前、准时和滞后相关值，码跟踪环对超前、滞后相关值进行处理实现对伪码的跟踪和伪距测量，而载波跟踪环、载噪比估计模块和电文处理模块则分别对即时支路相关值进行处理从而实现载波跟踪、载噪比估计和电文解调。在扩频系统中，信号捕获、载波跟踪和数据解调的性能均与接收机相关器输出的信噪比有直接关系，导航信号发生畸变情况下会引起相关函数形变和延迟，将影响导航接收机的跟踪测距和载噪比估计。

本文主要研究在国际民航组织(InternationalCivilAviationOrganization,ICAO)二阶阶跃畸变模型下信号畸变参数对导航接收机载噪比估计的影响及载噪比与畸变参数之间的关系。首先介绍了ICAO二阶阶跃畸变模型和导航接收机载噪比估计模型，接着从数学上推导了在高斯白噪声条件下接收机采用相干、非相干早晚处理的载噪比输出与信号畸变参数之间的解析表达式，并对前端滤波器带宽和信号畸变参数对载噪比估计的影响进行了理论分析和仿真验证，分析过程中假设接收机跟踪误差量足够小而且跟踪环路不失锁。

1 数学模型

1.1 导航信号畸变模型

国际民航组织提出采用二阶阶跃模型来描述信号畸变，该模型将导航信号可能的故障分为三类：数字畸变(ThreatModelA,TMA)，模拟畸变(ThreatModelB,TMB)，数字模拟畸变(ThreatModelC,TMC)[1-3]。数字畸变反映卫星导航数据处理单元的数字部分故障，表现为伪码的下降沿比正常下降沿超前或滞后，接收机本地伪码信号与数字畸变信号的相关峰会在峰顶出现扁平区[4-6]。模拟畸变模型对应卫星信号生成流程中若干模拟处理单元故障，可以等效于正常信号经过一个二阶阻尼振荡滤波器之后的响应。数字模拟畸变则由星上信号生成单元的数字器件故障和模拟器件故障产生，信号幅度出现二阶阻尼振荡，且伪码下降沿比正常伪码超前或滞后[7-9]。

ICAO二阶阶跃模型下的信号畸变产生，如图1所示。

图1 ICAO畸变信号生成框图Fig.1 Block diagram of abnormal signal generationusing ICAO 2nd-OS model

畸变信号生成可表述为

s′(t)=[s(t)+dΛ(t)]⊗h(t)

(1)

其中：s(t)，s′(t)分别表示正常信号和畸变信号；dΛ(t)表示数字畸变量；h(t)表示模拟畸变滤波器的单位脉冲响应；⊗为卷积运算符号。

数字畸变量与正常信号的互相关函数时域表达式为[2-3]

(2)

对式(2)进行傅里叶变换，则其频域形式可写为

(3)

式中,NTc为相关积分时间，Tc为码片宽度，Λ为数字畸变量。

模拟畸变滤波器的单位脉冲响应时域形式为[4]

(4)

式中：σ,ωd分别为二阶阻尼振荡的衰减频率和振荡频率；u(t)为单位阶跃函数。

1.2 导航接收机载噪比估计模型

导航接收机的载噪比估计模型如图 2所示，含有高斯白噪声的导航信号经过接收机前端滤波器滤波后分别与超前、即时、滞后本地伪码进行相关积分运算，超前、滞后相关值以及跟踪处理模块用于维持伪码跟踪环路对信号的正常跟踪。当码环处于跟踪状态时载噪比估计器处理即时支路相关值产生当前时刻的载噪比估计值。

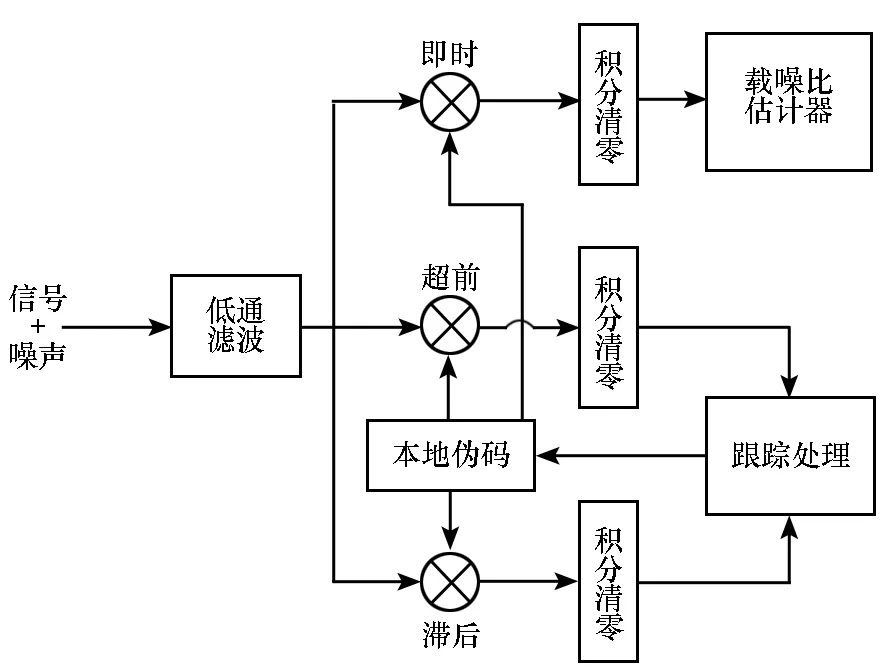
图2 导航接收机载噪比估计模型Fig.2 CNR estimation model in GNSS receiver

即时支路的相关器输出为[10-12]

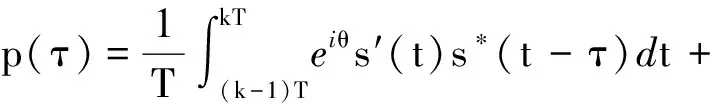
(5)

式中：(·)*为共轭运算；T为相关积分时间；τ为信号传播时延估计误差；θ为载波相位估计误差；βr为接收机前端滤波器等效带宽；S(f)，S′(f)分别为正常信号和畸变信号的频域形式；n(t)为零均值复高斯白噪声。

2 载噪比估计

2.1 相干处理

采用相干处理的载噪比估计器只使用即时支路相关值的实部，估计器输入可写为[10]

(6)

其中Re[•]为取实部运算。

即时支路相关值实部的期望值为

(7)

式中，Cs为接收信号功率，Gs(f)为信号的归一化功率谱密度，R(f)为数字畸变量与正常信号的互功率谱密度，H(f)为模拟畸变单位脉冲响应的频域形式。

即时支路相关值实部的方差为

(8)

交换积分次序后为

(9)

式中Gw(f)为噪声功率谱密度频域表示。

因此接收机采用早晚相干处理的载噪比估计为

(10)

式中b为相干积分运算的等效带宽。显然当τ=0且θ=0时载噪比估计取得最大值，此时

(11)

2.2 非相干处理

采用非相干处理的载噪比估计器使用即时支路相关值的包络，其输入可以表示为[11]

(12)

考虑到n(t)为零均值复高斯白噪声，根据概率统计理论可知，即时支路相关值的分布也为高斯的，其包络值λNELP将服从莱斯分布。当导航接收机稳定跟踪时，解扩后的信号功率远大于噪声功率，此时呈莱斯分布的准时支路相关值包络将趋近于高斯分布。

因此，即时支路相关值包络的期望值可近似为

(13)

同样地，即时支路相关值包络的方差可以近似为

(14)

当τ=0时式(14)采用非相干处理计算的载噪比估计取得最大值，此时有

(15)

3 仿真分析

考察在接收含有高斯白噪声的二进制相移键控(BinaryPhaseShiftKeying,BPSK)导航信号时ICAO二阶阶跃畸变模型对接收机载噪比估计的影响。假设导航信号扩频码码率为1.023MHz，输入载噪比设定为40dBHz，相关积分时间为20ms。采用相干、非相干处理时不同畸变模型下导航信号的载噪比与前端滤波器带宽的关系分别如图3和图4所示，从图中可以看出前端滤波器带宽对数字畸变模型下信号载噪比估计的影响较小，TMB和TMC情况下在前端滤波器带宽为12MHz时载噪比出现相对极大值点，但仅比正常的载噪比高出0.1dBHz左右。采用相干、非相干处理时TMA情况下载噪比估计与数字畸变量参数的关系如图5所示，可以看出随着畸变量的变大载噪比估计值会略有变大，但总体而言在数字畸变参数变化范围内对载噪比的影响在10-2量级，基本上可以忽略不计。采用相干、非相干处理时TMB情况下载噪比估计与模拟畸变量参数的关系分别如图6和图7所示，从图中可以看出减小模拟畸变衰减频率或增大振荡频率会提高载噪比估计值，畸变参数变化范围内载噪比变化在0.1dBHz左右。

图3 相干处理时载噪比与前端滤波器带宽关系Fig.3 CNR versus front-end filter bandwidth using CELP

图4 非相干处理时载噪比与前端滤波器带宽关系Fig.4 CNR versus front-end filter bandwidth using NELP

图5 数字畸变量与载噪比估计关系Fig.5 CNR versus TMA parameter using NELP and CELP

图6 相干处理时载噪比与模拟畸变参数关系Fig.6 CNR versus TMB parameter using CELP

图7 非相干处理时载噪比与模拟畸变参数关系Fig.7 CNR versus TMB parameter using NELP

4 结论

ICAO二阶阶跃模型下导航信号发生畸变时前端滤波器带宽和畸变参数共同影响着接收机载噪比估计。从仿真结果可以看出，信号畸变参数对载噪比估计的影响幅度较小，相干处理和非相干处理时载噪比的变化基本一致。数字畸变且当前端滤波器带宽为12MHz时载噪比输出产生相对极大值点，模拟畸变时减小衰减频率或增大振荡频率将会使载噪比估计输出变大。总体而言，基于ICAO二阶阶跃模型的导航信号载噪比估计值并不能直接反映导航信号的畸变程度。

References)

[1]FontanellaD,PaonniM,EissfellerB.AnovelevilwaveformsthreatmodelfornewgenerationGNSSsignalstheoreticalanalysisandperformance[C]//Proceedingsofthe5thESAWorkshoponSatelliteNavigationTechnologiesandEuropeanWorkshoponGNSSSignalsandSignalProcessing, 2010.

[2]JakabAJ.QualitymonitoringofGPSsignals[D].Canada:UniversityofCalgary, 2001.

[3] 刘建成, 桑怀胜, 徐赟,等. 卫星导航信号异常对信噪比的影响[J]. 电讯技术, 2013,53(1):28-32.

LIUJiancheng,SANGHuaisheng,XUYun,etal.EffectofGNSSwaveformdistortionsonSNR[J].TelecommunicationEngineering, 2013, 53(1):28-32.(inChinese)

[4] 刘文祥. 卫星导航系统高精度处理与完好性监测技术研究[D]. 长沙:国防科学技术大学,2011.LIUWenxiang.Studyontechniquesofaccuracyaugmentingandintegritymonitoringforsatellitebasednavigationsystem[D].Changsha:NationalUniversityofDefenseTechnology, 2011.(inChinese)[5] 刘文祥. 卫星导航系统信号质量监测技术研究[D]. 长沙:国防科学技术大学,2007.

LIUWenxiang.Studyonthetechnologyofsignalqualitymonitoringforthesatellitenavigationsystem[D].Changsha:NationalUniversityofDefenseTechnology, 2007.(inChinese)

[6]AkosDM,PheltsRE,PullenS,etal.Signalqualitymonitoring:testresults[C]//Proceedingsofthe2000NationalTechnicalMeetingoftheInstituteofNavigation,Anaheim,CAJanuary26-28, 2000.

[7]AkosD.M,etal.GPS-SPSsignalqualitymonitor[C].IEEEPLANS,SanDiego,CA,March3-16, 2000.

[8]SaitohS,YoshiharaT,FukushimaS,etal.Detectionofanomalysignalbysignalqualitymonitoringreceiver[C]//Proceedingsofthe17thNTM,LongBeach,CA,September21-24, 2004.

[9]MitelmanAM,AkosDM,PullenS,etal.EstimationofICAOthreatmodelparametersforoperationGPSsatellites[C]//ProceedingsofIONGPS,Portland,Oregon,September24-27, 2002.

[10]BetzJW,KolodziejskiKR.Generalizedtheoryofcodetrackingwithanearly-latediscriminator.PartI:lowerboundandcoherentprocessing[J].IEEETransactionsonAerospaceandElectronicSystems, 2009, 45(4):1538-1550.

[11]BetzJW,KolodziejskiKR.Generalizedtheoryofcodetrackingwithanearly-latediscriminator.PartII:noncoherentprocessingandnumericalresults[J].IEEETransactionsonAerospaceandElectronicSystems, 2009, 45(4):1557-1564.

[12]BetzJW.Effectofpartial-bandinterferenceonreceiverestimationofC/N0:theory[C]//ProceedingsofIONNationalTechnicalMeeting,LongBeach,CA,January22-24, 2001.

Analysis of the influence of CNR estimation for GNSS receiver based on 2nd order step threat model

GUAN Gangqiang, PANG Jing, LIU Wenxiang, WANG Feixue

CNR(Carrier-to-NoiseRatio),animportantindicatortoevaluatethenavigationsignalquality,whichdirectlyaffectedtheglobalnavigationsatellitesystemreceiverperformancesofsignalacquisition,carriertracking,anddatademodulation.BasedonthedistortionmodelofICAO2OS(InternationalCivilAviationOrganization2ndOrderStep),theanalyticalexpressionsbetweenCNRestimationandthedistortionparametersofICAO2OSthreatmodelwereinducedbyusingbothcoherentearly-lateprocessingandnon-coherentearly-lateprocessing.AndtheinfluenceofdistortionparametersonCNRestimationerrorwasanalyzed.Theoreticalanalysisandsimulationresultsshowthatcarrier-to-noiseratioonlychangesinthe10-2orderofmagnitudewhentheTMA(ThreatModelA)parameterchangeswithinthesetrange,andcanreachabout0.1dBHzcausedbytheTMB(ThreatModelB)parameters.WhenincreasingtheTMBoscillationfrequencyanddecreasingtheattenuationfactorcanincreasetheestimatedCNR.ConsequentlythedistortionparametersofICAO2OSthreatmodelhaveasmallinfluenceontheCNRestimationloss.Therefore,usingtheoutputCNRoftheglobalnavigationsatellitesystemreceivertomonitorthenavigationsignalabnormalityisnotreliable.

carrier-to-noiseratioestimation;signaldistortion;anomalymonitor; 2ndorderstep

2014-11-07

教育部新世纪人才支持计划资助项目(NCET-08-0144)

关刚强(1986—)，男，河南鲁山人，博士研究生，E-mail：closetoqiang@163.com；王飞雪(通信作者)，男，教授，博士，博士生导师，E-mail：feixuewang_nnc@163.com

10.11887/j.cn.201504014

http://journal.nudt.edu.cn

TN

A