经纬网络充气机翼构形特征与气动性能分析*

张俊韬，侯中喜，郭 正

经纬网络充气机翼构形特征与气动性能分析*

张俊韬，侯中喜，郭 正

(国防科技大学 航天科学与工程学院， 湖南 长沙 410073)

将充气机翼应用于临近空间太阳能飞行器是具有创新性的设计概念。针对充气机翼构形特征和气动分析的相关问题，对构形特征进行分析和设计，并建立经纬网络充气机翼的模型；进一步运用数值方法，通过与标准翼型对比，分析二维充气机翼、三维经纬网络充气机翼的气动性能。数值分析结果表明，在设计的雷诺数条件下，充气机翼的气动性能相比于标准翼型有所降低。在此基础上，结合对流场结构和流动机理的研究，分析出导致充气机翼总阻力系数明显增加的主要原因是：充气机翼表面许多凹陷的局部区域所形成的涡结构，导致局部的摩阻有小幅的减小，但压差阻力大幅增加，最终使得总的气动性能有所降低。

充气机翼；构形特征；气动性能；流动机理

(CollegeofAerospaceScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China)

临近空间太阳能飞行器是一种以太阳能为主要能源，在临近空间实现持久驻留的无人飞行器。由于临近空间的低密度环境，要实现较低的飞行速度同时提供足够的升力，就需要较大的升力面，因此结构要做到大而轻，其翼展往往达到几十米甚至百米的量级，美国的“太阳神”就是一个典型的代表[1]。“太阳神”原型机HP01在2001年7月14日首次飞行试验，达到了22.8km的高度，此后又不断刷新飞行高度记录。然而，其另一架原型机HP-03由于上升过程中遭遇低空湍流而空中解体。因此大尺度太阳能飞行器结构安全性的隐患问题也暴露出来，如何做出“足够轻质”“足够安全”“气动性能足够好”的大尺度结构是临近空间太阳能飞行器发展的核心难题。

1 研究背景

运用充气机翼是一种创新的设计概念[2]，它采用轻质柔性复合材料制作而成，很容易实现结构的大尺度化，轻量化水平较刚性结构也有本质提升，大大降低了对充气结构自身刚性的需求，对飞行器能源系统性能要求也可以大大降低，并可极大降低结构在翼载荷中的比例，提高飞行器应用载荷和能源携带能力，同时提高结构安全性。飞行器平飞的需用功率的表达式为：

(1)

式(1)中，W表示飞行器重量，ρ大气表示密度，S表示机翼面积，CD表示阻力系数，CL表示升力系数。

可以看到，结构减重的效果是节省能源，气动性能的损失则会增加能源消耗。但具体分析发现，结构重量与气动性能对功率的影响比重是不同的，重量的效益更加明显。因此在大幅降低重量同时气动性能即便有所损失，总体的能源需求仍是可以降低的，充气机翼的价值就在于此。因此从概念设计的角度来说，充气机翼确实是一个非常有前景和意义的研究方向。其中，充气机翼由于外形的改变而导致气动性能较之标准翼型发生变化是气动问题的核心，也是张俊韬等的着眼点。

国内外已有关于充气机翼的总体设计、结构力学分析、智能材料变形、风洞、飞行试验等多方面的研究[3-14]，而针对气动特性的分析方面，文献[11]介绍了充气机翼的试验和计算，选择两种不同的翼型(Eppler398和NACA4318 )作为参考基准，通过分析发现充气机翼与标准翼型之间在流场特征上存在一些相似趋势，但又有所区别，进而预测了在较低雷诺数条件下，充气机翼的气动性能可以优于标准翼型。Simpson等[15]进行了风洞试验，利用流动可视化，观察到了当雷诺数小于5×104时，由于充气机翼表面凹凸不平，使得分离的发生较之于标准翼型有所延后。

国内对于充气机翼的研究起步较晚，但也开展了许多研究工作，取得了一些相关的研究进展。如王长国等[16]针对点阵式充气机翼，采用了逆向迭代的方法进行了保形设计。吕强等[17]研究了充气机翼的设计和工艺方法，同时进行了力学性能测试和飞行试验。王伟等[18]对充气机翼的承载能力进行了分析，同时进行了气动仿真计算。

在构形分析方面，相对于较为成熟的二维设计方法，三维充气机翼的构形特征及其气动特性目前还没有被广泛研究。

2 构形特征分析

当前，多气梁整体式充气机翼构形是已有研究中大多采用的结构形式，其特点是在蒙皮内部沿弦长方向布置一系列拉条，如图1所示，这是传统二维充气机翼的设计方法。由于在各个拉条上均留有通气通道，使得各个气囊相互连通，整体上形成一个充气囊体，所以整个机翼内部压力均匀一致，对于防止风压变形有着相对较好的作用。

图1 传统二维充气机翼截面示意图Fig.1 Traditional 2d section of an inflatable wing

进一步考虑到实际三维机翼时，其直观的思路是将二维截面沿着翼展方向拉伸，如此一来这些约束就会形成一系列矩形带条。这种方法虽然比较通用，但要达到较好的逼近效果，其二维截面约束需要设计得很密。这样在三维成型时，仅仅约束带条就增加了很多材料重量，使得充气结构的总体重量和复杂度大幅增加，导致充气机翼的重量优势不再明显，同时其结构刚度和气动性能方面与刚性机翼相比可能还有所损失。

基于此，解决上述问题可以采用经纬网络的构形方法，如图2所示，采用经向(翼展方向)和纬向(弦长方向)的点阵，每隔一定的距离布置一个拉条，这样形成三维的充气机翼，其结构重量将大大下降，其外形也逼近所要设计的标准翼型，但仍需要进一步具体分析。

图2 经纬网络结构示意图Fig.2 Sketch of network structure

分析其构形特征，为方便考虑，避免涉及复杂三维曲面形状等内容，可以把问题简化为先只考虑边界线，待确定了边界线后，不需要知道曲面的具体精确构形，只要以较好的方式进行拟合逼近，即可以得到满足气动性能分析的构形特征。

2.1 分析两个拉条约束之间蒙皮弧段的形状

从一般受力的角度分析，首先进行以下假设：

1)忽略蒙皮的自重；

2)忽略材料本身的变形；

3)不考虑节点处的褶皱。

在以上假设条件下，当内部因充入气体而具有均匀的压力分布时，两个拉条约束之间的蒙皮段将向外鼓出。到目前为止，蒙皮弧段的形状还没有确定，考虑到最小势能原理，即在所有可能的位移场中，其最终的位移使得总势能最小。因此，可以认为圆弧是最为合理的形状，那么在这种推论下，图3所示的情况是最可能形成的稳定状态。

根据上述假设和分析，对这种蒙皮形成圆弧段的推论是否满足几何位置关系以及受力平衡条件进行证明。

如图3所示，两个拉条之间的长度为L，内部压力为Δp，取一半蒙皮段AB进行受力平衡分析。

图3 两个拉条间蒙皮弧段的形状Fig.3 Shapes of the skin arc between two webs

在竖直方向：

(2)

在水平方向：

T1cosθ+Δph=T2

(3)

分别取A，B点的法线相交于点O，AO长为R，BO长为R′则有：

(4)

(5)

将式(4)、式(5)分别代入式(2)、式(3)，则有：

(6)

(7)

用式(6)除以式(7)，则有：

(8)

对于式(8)，若蒙皮段的形状为圆弧，则：在几何关系上，根据圆的半径相等，有R′=R；在力学关系上，根据圆弧段的内部张力处处均匀，有T2=T1。

将R′=R和T2=T1代入式(8)，通过化简，可以推得左右两边恒等。至此，就证明了蒙皮形成的圆弧是可以同时满足几何关系和受力平衡的最合理的形状。

另外，对于两个拉条的长度不等的情况，其分析方法实际上与图3所示的情况类似，只不过相当于偏转了一个角度，因此仍然可以得到以蒙皮弧段为圆弧是合理的这一结论。

2.2 确定构形特征

分别对经向和纬向进行分析。

2.2.1 纬向截面的特征

不失一般性，考虑最简化的情况，即一个充气机翼在纬向截面只有两条约束，即由三段圆弧组成，如图4所示。

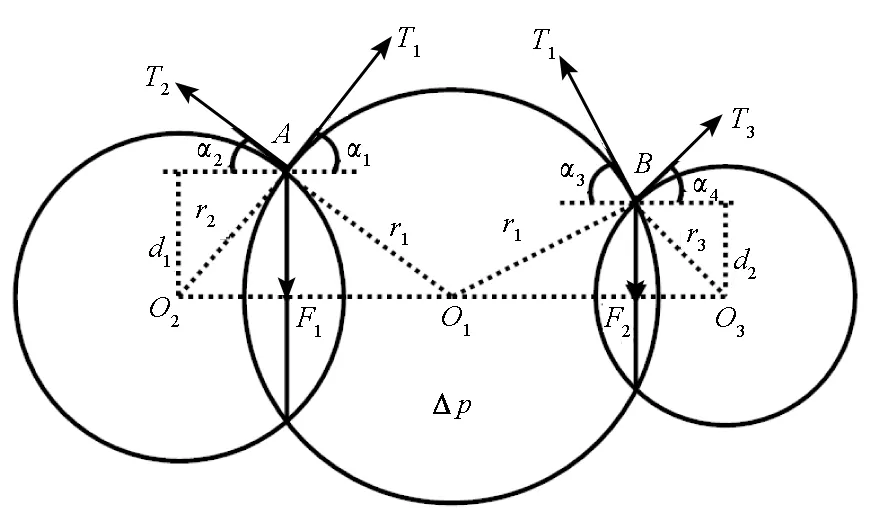
图4 三个相交圆的受力分析Fig.4 Force analysis of three crossing circles

在平衡状态下A点和B点满足受力平衡。节点A处受到圆O1和圆O2两段圆弧在此点处切线方向的表面内力T1，T2(其方向与水平之间的夹角分别为α1，α2)，节点B处同理，以及公共弦的拉应力为F1和F2。

在垂直方向上，应有：

F1=T1sinα1+T2sinα2

(9)

F2=T1sinα3+T2sinα4

(10)

作为未知量的公共弦拉应力F1和F2取决于T1，T2，T3，但在平衡状态下可以不必关心，因为总存在合适的F1和F2使得式(9)、式(10)成立。

在水平方向上，应有：

T1cosα1=T2cosα2

(11)

T1cosα3=T3cosα4

(12)

根据圆弧段的表面内力表达式，T1，T2以及T3可以表示为：

T1=Δpr1

(13)

T2=Δpr2

(14)

T3=Δpr3

(15)

同时，根据几何关系，有：

(16)

(17)

(18)

(19)

将式(13)、(14)、(16)、(17)代入式(11)，将式(13)、(15)、(18)、(19)代入式(12)，化简后可以推得，式(9)和式(10)均为恒等式，则节点A和B处的受力平衡在三个圆相交的条件下是可以实现的。这就证明了上述三个圆相交所构成的基本构形是合理的，同理可以推论至任意布置多个圆的情况，因此说明以此构形为基础的充气机翼纬向截面构形是可行的。

2.2.2 经向截面的特征

同理可知，对称翼型沿经向的截面形状是不变的，因此在经向的某个截面的形状应该是由如图5所示的半径均相等的圆弧段构成的。

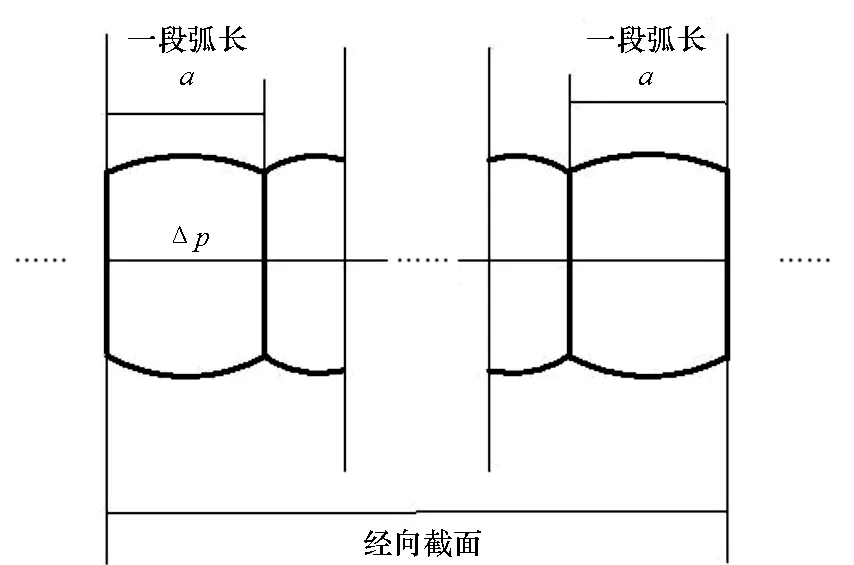
图5 经向截面形状Fig.5 Shapes of section of longitude

.2.3 经纬网络模型

至此，纬向和经向的边界线都已确定，它们是一组由圆弧段构成的边框。然而，对于实际工程应用而言，任何材料都会存在变形，所以需要再次强调的是，利用圆弧段描述充气机翼构形特征的方法只是一种合理的近似，实际机翼充气成型后每个弧段可能不完全是圆弧，但是必然是比较逼近的。那么由这些边界所围成的三维蒙皮表面的形状即为网格化的近似球面，则三维经纬网络的充气机翼模型的局部示意图如图6所示。以上构形特征分析是充气机翼气动分析的基础。

图6 局部经纬网络模型示意图Fig.6 Sketch of local network model

3 气动特性分析

3.1 计算模型和条件

基于前述构形特征分析，气动特性分析选择以NACA0012为标准翼型而建立的充气机翼的气动外形为研究对象。具体来说，纬向构造由30个圆相交所构成的截面，经向分别进行二维拉伸和三维经纬网络构造，形成的计算模型如图7(a)和图7(b)所示。计算条件的相关参数见表1。

(a) 二维拉伸构形(a) Model of 2d stretching inflatable

(b) 三维经纬网络构形(b) Model of 3d network inflatable图7 数值仿真的模型Fig.7 Model for numerical simulation

参数值高度20km温度216．65K压力5529．31Pa密度0．0889099kg/m3动力粘度1．42161×10-5N·s/m2速度20m/s机翼弦长2．4m对应雷诺数300000

3.2 CFD方法

3.2.1 控制方程

低速翼型所适用的稳态不可压缩流动的控制方程为：

1)连续方程：

divV=0

(20)

V是流体速度矢量，div代表散度运算符。

2)动量方程：

(V)2V

(21)

3.2.2 网格划分

采用C型网格拓扑来划分计算域，如图8(a)所示。

(a) C型网格拓扑(a) Topology of C type grids

(b) 近壁面网格细节(b) Detail of grids near wall图8 网格示意图Fig.8 Sketch of grids

计算域的长度和宽度为弦长的30倍，近壁面的第一层网格高度为弦长的10-4，核算得到对应的y+最大为2，如图8(b)所示，满足计算近壁面边界层的要求。

采用商业代码FLUENT6.3.26作为求解器，利用其三维、有限体积法，求解稳态不可压Navier-Stokes方程。如图8(a)所示：入口边界条件设置为速度入口“Velocityinlet”，具体要给定速度的大小和方向，来流的基本参数仍见表1；出口边界条件设置为压力出口“Pressureoutlet”，具体要给定出口的表压值。壁面边界条件设置为无滑移绝热壁；两侧设置为对称边界条件“symmetry”，这样计算出的三维模型为无限展长。根据文献[19]，选择SSTk-ω湍流模型，其适合翼型的数值模拟，结果精度较好。

3.3 结果分析

3.3.1 升阻系数

如图9所示，对于升力而言，在迎角较小的情况下，二维拉伸和三维经纬网络两种充气机翼构形的升力系数与NACA0012均十分接近，当迎角增大时，充气机翼的升力系数逐渐小于NACA0012的，说明在大迎角条件下充气机翼构形的升力系数有所损失，但同时可以看到充气机翼的失速更晚发生，总体来讲升力系数损失不大，这个结论与文献[15]中的情况是类似的。

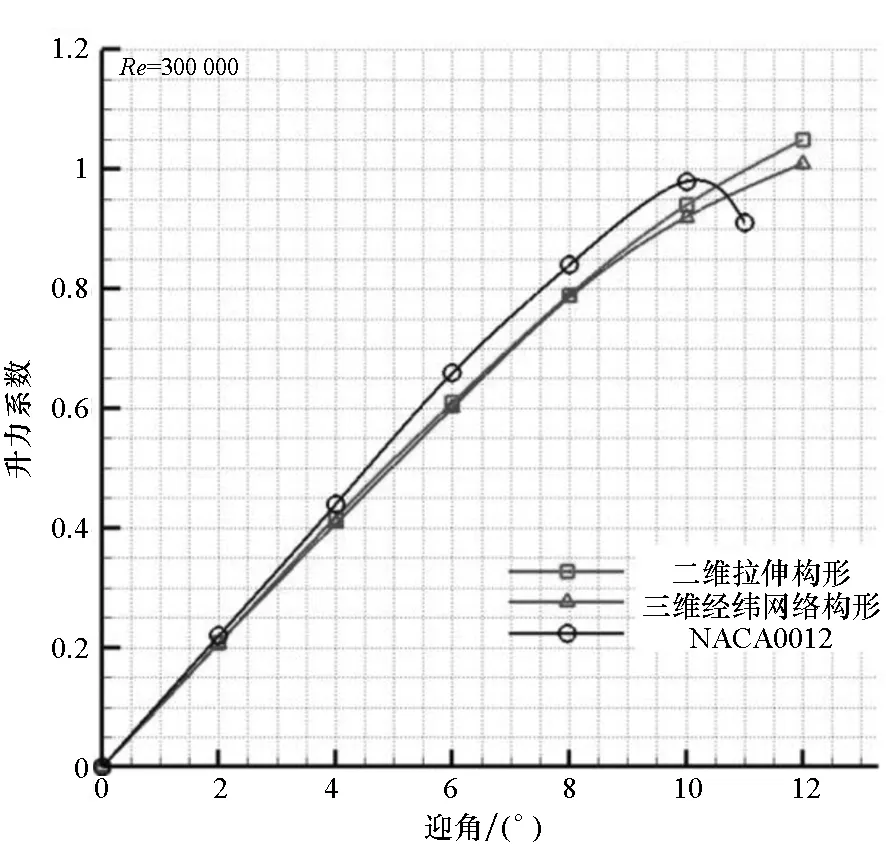
图9 升力系数曲线对比Fig.9 Comparison of lift coefficient curves

图10 极曲线对比Fig.10 Comparison of polar curves

对于阻力而言，如图10所示，可以看到充气机翼的阻力系数相比NACA0012均有了显著的增大，由此可以推断在此雷诺数条件下，充气机翼相比NACA0012而言升阻比是降低的，即整体的气动性能将有所损失。同时进一步可以看到，二维拉伸构形与NACA0012相比阻力系数已显著增大，三维经纬网络构形的阻力系数与二维拉伸构形相比又有所增加。

如表2所示，从具体数据分析其原因：由于二维拉伸构形相比光滑的NACA0012存在许多凹陷区域，导致的局部压差阻力增加了很多，因此总阻力的分布中，压差阻力比摩阻高了一个量级，而在三维经纬网络构形中，可以看到压差阻力与摩阻所占的比重与二维拉伸构形类似，但同时压差阻力和摩阻都进一步有所增加，且压差阻力增加得更多。以上分析说明三维经纬网络构形网格化结构进一步增加了形状阻力，因而气动性能较之二维拉伸构形进一步有所损失。

表2 2°迎角下阻力系数的对比

3.3.2 流场特征和机理分析

气动系数的对比说明了充气机翼外形致使气动性能下降的主要原因是局部凹陷区域的摩阻和压差阻力的变化，其中压差阻力有较为明显的增加。本节从流场结构特征和流动机理的角度进一步分析产生这种现象的原因。

1)纬向截面特征。

针对某一处局部的凹陷区域的若干纬向截面进行流场特征分析，对于二维拉伸构形，如图11所示，由于其拉伸构形的各个纬向截面完全一致，因此本质上仍然具有二维的流动特征。从图11中可以明显看出，在此处凹陷区域形成了回流区，且各截面的流动状态保持一致。

图11 二维拉伸构形的局部流线Fig.11 Local streamlines of 2d stretching inflatable

进一步，如图12所示，在此处凹陷部分壁面附近的一定区域内，流体的速度很小并形成回流，意味着该区域内流体的动能很大一部分都转化为内能，流动的能量损失就是阻力增加的根本原因。此外，通过该速度矢量图还可看到壁面附近附面层的发展过程。

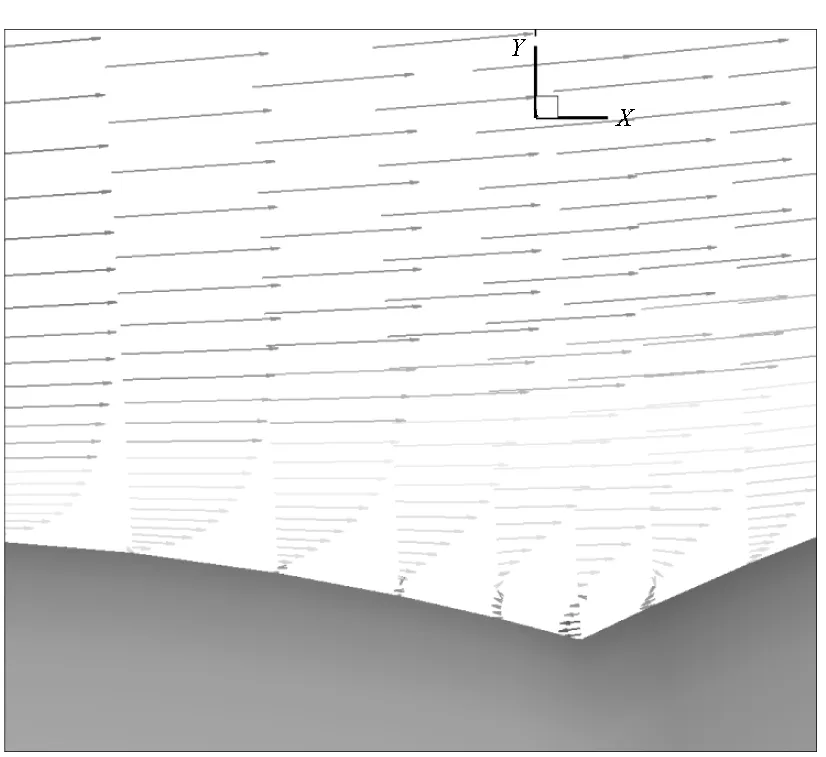
图12 壁面附近速度矢量图Fig.12 Velocity vectors near the wall

对于三维经纬网络构形，如图13所示，其与二维拉伸构形的构形区别主要在于每个纬向截面的形状是不同的，因此在垂直于纬向截面的方向上看去，不同的截面边界的高度是不同的。这样导致在该区域不同截面所产生的旋涡结构特征也发生了变化，这必然会导致气动力的变化，因而各个截面累加起来的效果就与二维拉伸构形的结果产生了差别。

图13 三维经纬网络构形的局部纬向流线Fig.13 Local streamlines of latitude of 3d network inflatable

2)经向截面特征。

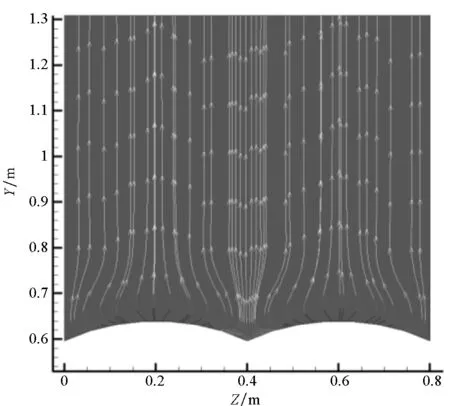
与纬向截面同理，在三维经纬网络构形的某处局部凹陷区域垂直于体轴方向取若干经向截面，如图14所示，进一步观察壁面附近流线的形状以及发展状态。

图14 三维经纬网络构形的局部经向截面Fig.14 Section of longitude of 3d network inflatable

如图15(a)所示，由于经向平面1位于凹陷区域上游的圆弧最高位置附近，尚未出现明显的纬向流动，只是在壁面附近靠近凹陷位置的最低处向圆弧最高点过渡的方向上产生了流线的弯曲；如图15(b)所示，经向平面2的位置已经逐渐靠近纬向凹陷区域的最低点，因此可以看到此处已经产生了纬向的流动，在靠近凹陷位置的最低处流线向两侧出发，并流向圆弧最高点；如图15(c)所示，经向平面3位于纬向凹陷区域的最低点附近，可以看到此处的纬向流动已经充分发展，并产生了纬向旋涡回流，说明在凹陷位置的最低处纬向流动也已经造成了比较明显的流动损失，同时此处的经向涡结构也说明了图13所示的不同纬向截面的涡是如何过渡的。

对于二维拉伸构形，容易知道其经向截面的流线分布必定是垂直于壁面的，因而不会产生纬向流动。以上分析表明，三维经纬网络构形由于其构形特征所导致的纬向流动损失是其气动性能进一步降低的本质原因。

(a) 经向平面1的流线图(a) Streamlines of longitude on plane 1

(b) 经向平面2的流线图(b) Streamlines of longitude on plane 2

(c) 经向平面3的流线图(c) Streamlines of longitude on plane 3图15 三维经纬网络构形的局部经向流线图Fig.15 Local streamline charts of 3d network inflatable

3)表面极限流线。

研究表面极限流线的分布状态对于判定流动的分离和再附有重要的意义，如图16所示，仍然取局部凹陷区域进行表面分析。

图16 三维经纬网络构形的局部极限流线Fig.16 Local limiting streamlines of 3d network inflatable

根据三维流动分离理论[20]，在物面上，分离线附近的极限流线分别向分离线收拢，并以分离线为渐近线；而再附线附近的极限流线是分别向外发散的，并以再附线为渐近线。

根据物面上奇点分布规律，如果分离线以奇点为起始点，那么该奇点必为鞍点，如果再附线从奇点出发那么该奇点必为节点，如果再附线进入奇点那么该奇点必为鞍点。从图16中可以看出，左右两条分离线均从中间鞍点起始；同时也可以明显地看到，从左右两侧节点出发，分别出现两条再附线，两条再附线终止于靠近凹陷处最低点附近的鞍点。

二维拉伸构形的极限流线拓扑结构如图17所示，同样根据分离和再附的判据，可以看出凹陷区域靠前的位置存在一条极限流线靠近收拢的渐进线，此线为分离线，而靠后的位置存在一条极限流线离开发散的渐近线，此线为再附线。

图17 二维拉伸构形的局部极限流线Fig.17 Local limiting streamlines of 2d stretching inflatable

至此，对比二维拉伸构形和三维经纬网络构形的表面极限流线分布可以看出，二维拉伸构形由于截面形状不变且无限展长，因此仍然保持二维的流动特征，即不存在纬向流动，只存在沿弦长方向的流动；而三维经纬网络构形形成的凹坑结构则出现了纬向的流动，在凹陷的局部区域形成了特定的流场结构，这也从流动机理上解释了气动性能产生差异的原因。

4 结论

1) 通过一般受力，分析了经纬网络充气机翼构形的特征，为气动特性的研究提供了计算模型和分析基础；

2)在设计雷诺数条件下，充气机翼的气动性能相比于标准翼型有所降低，气动性能的损失主要体现在升力系数略有降低、阻力系数明显增加；

3) 通过对流场结构的分析，从机理上解释了气动性能降低的原因在于众多的局部凹陷区域使得局部流动分离产生旋涡，且三维经纬网络构形相比于二维拉伸构形产生了纬向流动，因此进一步加剧了能量的耗损。

References)

[1]NollTE,BrownJM,Perez-DavisME,etal.InvestigationoftheHeliosprototypeaircraftmishap[R].Hampton:NASAreport.

[2]CadoganD,ScarboroughS,GleesonD,etal.Recentdevelopmentandtestofinflatablewing[C]//Proceedingsof47thAIAA/ASME/ASCE/AHS/ASCStructures,StructuralDynamics,andMaterialsCon,Newport,RhodeIsland,AIAA-2006-2139, 2006.

[3]SimpsonA,JacobJ,SmithS,etal.BIGBLUEII:marsaircraftprototypewithinflatable-rigidizablewings[C]//Proceedingsof43rdAIAAAerospaceSciencesMeetingandExhibit,Reno,Nevada,AIAA-2005-813, 2005.

[4]ReasorDA,LeBeauRP,SmithSW,etal.Flighttestingandsimulationofamarsaircraftdesignusinginflatablewings[C]//Proceedingsof45thAIAAAerospaceSciencesMeetingandExhibit,Reno,Nevada,AIAA-2007-0243, 2007.

[5]ReasorDAJr,LeBeauRPJr.NumericalstudyofbumpyairfoilcontrolforlowReynoldsnumbers[C]//Proceedingsof37thAIAAFluidDynamicsConferenceandExhibit,Miami,FL,AIAA-2007-4100, 2007.

[6]SmithSW,LeBeauRP,SeiglerTM,etal.Testingofcompactinflatablewingsforsmallautonomousaircraft[C]//Proceedingsof49thAIAA/ASME/ASCE/AHS/ASCStructures,StructuralDynamics,andMaterialsConference,Schaumburg,IL,AIAA-2008-2216, 2008.

[7]LeBeauRPJr,GilliamTD,SchloemerA,etal.Numericalcomparisonofflowoverbumpyinflatableairfoils[C]//Proceedingsof47thAIAAAerospaceSciencesMeetingIncludingTheNewHorizonsForumandAerospaceExposition,Orlando,Florida,AIAA-2009-1306, 2009.

[8]ThamannM.AerodynamicsandcontrolofadeployablewingUAVforautonomousflight[D].USA:UniversityofKentucky, 2012.

[9]HauserT,JohansenTA,LeBeauRPJr.ComputationaloptimizationofalowReynoldsnumberinflatableairfoil[C]//Proceedingsof20thAIAAComputationalFluidDynamicsConference,Honolulu,Hawaii,AIAA-2011-3534, 2011.

[10]TakahashiD,LeBeauRPJr.ComputationalinvestigationofReynoldsnumbereffectsonflowoverinflatableairfoils[C]//Proceedingsof49thAIAAAerospaceSciencesMeetingincludingtheNewHorizonsForumandAerospaceExposition,Orlando,Florida,AIAA-2011-337, 2011.

[11]GhobadiKJ,LeBeauRPJr,HauserT.Computationaltestingofinflatableairfoilsforimproveddesign[C]//Proceedingsof50thAIAAAerospaceSciencesMeetingincludingtheNewHorizonsForumandAerospaceExposition,Nashville,Tennessee,AIAA-2012-1213, 2012.

[12]GhobadiKJ,PiferE,LeBeauRPJr,etal.Acomputationalandexperimentalinvestigationofflowoveraninflatablewing[C]//Proceedingsof30thAIAAAppliedAerodynamicsConference,NewOrleans,Louisiana,AIAA-2012-2899, 2012.

[13]ZhangF,GhobadiKJ,SpencerG,etal.Examinationofthree-dimensionalflowoverachamberedinflatablewing[C]//Proceedingsof52ndAIAAAerospaceSciencesMeetingincludingtheNewHorizonsForumandAerospaceExposition,NationalHarbor,MD,AIAA-2014-0556, 2014.

[14]AllredRE,HoytAE,HarrahLA,etal.Lightcuringrigidizableinflatablewing[C] //Proceedingsof45thAIAA/ASME/ASCE/AHS/ASCStructures,StructuralDynamicsandMaterialsConference,PalmSprings,California,AIAA-2004-1809, 2004.

[15]SimpsonA,SanthanakrishnanA,JacobJ,etal.Flyingonair:UAVflighttestingwithinflatablewingtechnology[C] //Proceedingsof3rd“UnmannedUnlimited”TechnicalConference,WorkshopandExhibit,Chicago,Illinois,AIAA-2004-6570, 2004.

[16] 王长国, 刘远鹏 崔宇佳, 等. 逆向迭代的点阵式充气机翼三维保形分析[J]. 哈尔滨工业大学学报，2013, 45(9): 31-34.

WANGChangguo,LIUYuanpeng,CUIYujia,etal.Inverseiterativethree-dimensionalinitialshapeanalysisofinflatablewing[J].JournalofHarbinInstituteofTechnology, 2013, 45(9): 31-34. (inChinese)

[17] 吕强, 叶正寅, 李栋. 充气结构机翼的设计和试验研究[J]. 飞行力学，2007, 25(4): 77-81.

LYUQiang,YEZhengyin,LIDong.Researchondesignandtestofinflatablewing[J].FlightDynamics, 2007, 25(4): 77-81. (inChinese)

[18] 王伟, 王华, 贾清萍. 充气机翼承载能力和气动特性分析[J]. 航空动力学报, 2010, 25(10): 2296-2301.

WANGWei,WANGHua,JIAQingping.Analysisonbearingcapacityandaerodynamicperformanceofaninflatablewing[J].JournalofAerospacePower, 2010, 25(10): 2296-2301. (inChinese)

[19]EleniDC,AthanasiosTI,DionissiosMP.Evaluationoftheturbulencemodelsforthesimulationoftheflowoveranationaladvisorycommitteeforaeronautics(NACA) 0012airfoil[J].JournalofMechanicalEngineeringResearch, 2012, 4(3):100-111.

[20] 张涵信. 分离流与漩涡运动的结构分析[M]. 北京：国防工业出版社, 2005.

ZHANGHanxi.Structuralanalysisofseparatedflowsandvortexmotion[M].Beijing:NationalDefenseIndustryPress, 2005. (inChinese)

Analysis of configuration characteristics and aerodynamic performance on longitude-latitude network inflatable wings

ZHANG Juntao, HOU Zhongxi, GUO Zheng

Theinflatablewingisagoodinnovationalconceptionforthenearspacesolar-poweredaircraft.Theproblemsofconfigurationcharacteristicsandaerodynamicanalysisofinflatablewingsweretakenastheaimofthecurrentstudy.First,configurationcharacteristicswereanalyzedanddesigned.Thenthemodelof3dnetworkinflatablewingwasdeveloped.Withcomputationalfluiddynamicsmethod,aerodynamicperformancesof2dinflatablewingprofileand3dnetworkinflatablewingwerestudied.Numericalsimulationresultshowsthattheaerodynamicperformancesof2dinflatablewingprofileand3dnetworkinflatablewinghavereducedslightlyatthedesignReynoldsnumber.Meanwhile,withthestructureofflowfieldandmechanismanalysis,thereasonforthetotaldragcoefficientsofinflatablewingsincreasingsignificantlyliesinthat,inthosebumpyareasoftheinflatablewing,vortexeswhichcausethefrictiondraghasareductioninsomeextent,butthepressuredraghasasignificantincrease,sothetotalaerodynamicperformancedecreases.

inflatablewings;configurationcharacteristic;aerodynamicperformance;flowmechanism

2015-03-31

航空科学基金资助项目(20145788006)

张俊韬(1986—)，男，天津人，博士研究生，E-mail：zzt136@163.com；侯中喜(通信作者)，男，教授，博士，博士生导师，E-mail：hzx@sina.com

10.11887/j.cn.201504007

http://journal.nudt.edu.cn

V

A