基于离散Beam梁法的变截面钢板弹簧建模及仿真

龚海清，杨啟梁，陈彦龙，袁 爽，罗仁宏

（武汉科技大学汽车与交通工程学院，湖北 武汉，430081）

钢板弹簧（以下简称板簧）是汽车悬架系统的组成部分，不仅可以作为悬架的弹性元件，还可兼作其导向机构。少片式变截面板簧具有应力分布均匀、结构简单、质量小、噪声低等优点，使得其在车辆中得到较广泛应用，已经成为汽车轻量化研究的重要内容之一［1］。在变截面板簧的动力学仿真中，利用虚拟样机技术准确建立弹簧的模型并进行合理应用一直是其难点所在［2］。在ADAMS软件环境下，常见的板簧建模方法有3种：有限元法、SAE三连杆法和离散Beam梁法。有限元法建模用于单一研究板簧特性时或研究结构简单的板簧系统时，其计算精度高，但应用于整车或复杂板簧系统的建模时，由于系统自由度较多，不易收敛，则难以获得理想的计算结果［3］。SAE三连杆法是基于三连杆理论简化模型的建模方法，该方法建模简单、计算收敛快，且结合其他模型装配仿真优化比较容易，但是计算出的刚度值精度不高，一般用于对板簧刚度值准确性要求不是很高的情况［4］。离散Beam梁法是基于离散理论而形成的一种简化建模方法，其建模特点是将每片板簧切割成n段等长度的片段，将每个片段看作是集中质量的刚体块，再通过无质量的柔性离散梁连接起来，软件系统会根据板簧的截面和材料自动计算出梁单元的刚度矩阵和阻尼矩阵，板簧的曲率由每个刚体块之间的节点连接位置确定。采用离散Beam梁法建立板簧模型，仿真计算收敛快，精度较高，适合用于板簧动力学仿真中的建模［5］。但其在变截面板簧动力学建模中的应用尚未见相关研究。为此，本文采用离散Beam梁法，借助多体动力学软件ADAMS对变截面板簧进行动力学建模，并将仿真计算的刚度与试验测试结果对比，以验证模型的正确性。

1 变截面板簧数学模型的建立

变截面板簧的车轴安装位置部分为等长等厚，其余部分各个截面的尺寸不同，其结构简图如图1所示。

图1 变截面板簧结构简图Fig.1 Structural diagram of taper leaf springs

在多体动力学软件ADAMS中将板簧片离散成若干个刚体块，相邻的刚体块之间用无质量的离散Beam梁连接，各片板簧之间添加接触约束。刚体块之间连接的无质量Beam梁阻尼矩阵和刚度矩阵与板簧的自身结构属性有关，ADAMS软件会根据板簧各簧片所选取的材料及其截面形状自动计算得到。刚体块质心坐标如图2所示，在相邻两个刚体质心处建立坐标系I和J，Beam在I、J之间传递6个与I、J之间相对位移和速度成线性关系的相互作用力［6］。作用力的计算方程如下：

图2 刚体块质心坐标示意图Fig.2 Diagram of the barycentric coordinates of rigid body

式中：Fx、Fy、Fz为I、J之间传递的3个轴向力，N；Tx、Ty、Tz为I、J之间传递的绕各轴的转矩，N·mm；L为I、J之间沿X 轴向的初始距离，mm；x、y、z分别为I、J之间3个轴向力作用下产生的相对位移，mm；Ax、Ay、Az分别为I、J之间绕各轴的转矩作用下产生的相对位移，mm；Vx、Vy、Vz分别为I、J之间3个轴向力作用下产生的相对速度，mm／s；wx、wy、wz分别为I、J点之间绕各轴的转矩作用下产生的相对速度，mm／s；Kij（i，j＝1，2，3）为线性刚度，N·mm－1；Kij（i，j＝4，5，6）为扭转刚度，N·mm·（°）－1；Cij（i＝1，2，…，6；j ＝1，2，3）为线性阻尼，N·s·mm－1；Cij（i＝1，2，…，6；j＝4，5，6）为扭转阻尼，N·s·（°）－1。

基于离散Beam梁法建立的板簧模型，采用ADAMS中的Impact函数定义主片板簧与副片板簧之间的法向力。Impact函数表达式为：

式中：x0为I、J之间的碰撞触发距离，mm；x1为I、J之间的垂向距离，mm；x′为I、J之间的垂向相对速度，mm／s；d为阻尼完全起作用时I、J的距离，mm，d＞0；e为碰撞指数，一般取e＞l；k为碰撞刚度，N·mm－1；cmax为最大阻尼系数。

2 三维模型的建立

以某轻型客车后悬架板簧为例，利用离散Beam梁法，在ADAMS／Chassis的板簧编辑器中建立变截面板簧的三维模型。

2.1 建模参数

该客车后悬架板簧为变截面板簧，其主片前后段分别分成7段和8段刚体块，副片前后段分别为5段和6段刚体块。板簧的主要参数为：主片前段、后段长度分别为650、785mm，副片前段、后段长度分别为525、635mm，板簧宽度为64 mm，弹性模量E为200GPa，剪切模量G为79 GPa，材料密度为7.86g·cm－3，阻尼率为0.1。

板簧与车轴的安装类型选择下挂式。卷耳的类型为上卷曲，内径、外径分别为31、47mm。吊耳的质量为0.73kg，长度为140mm，转动惯量Ixy、Ixz和Iyz分别为36.7、683.5、881.0kg·m2。

2.2 约束与连接

卷耳与车架之间、吊耳与板簧之间、吊耳与车架之间以及每片板簧与车桥安装处均用衬套连接，板簧的各个连接衬套的轴向（X、Y、Z）和扭转（Rx、Ry、Rz）阻尼、刚度分别如表1和表2所示。

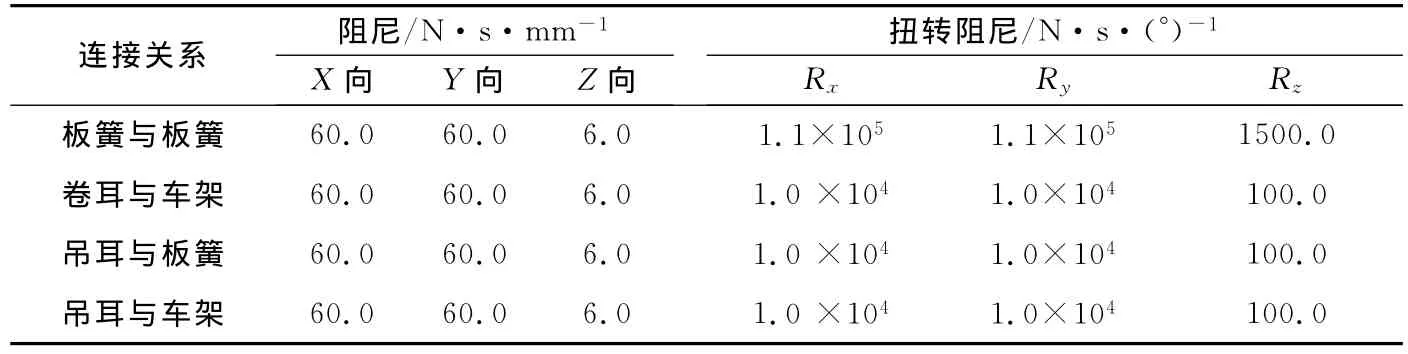
表1 板簧各个连接衬套的阻尼Table1 Damping of each bushing of leaf spring

表2 板簧各个连接衬套的刚度Table2 Stiffness of each bushing of leaf spring

2.3 三维模型的建立

在ADAMS／chassis的板簧编辑器中修改参数值，建立变截面板簧的三维模型，如图3所示。

图3 变截面板簧三维模型Fig.3 3Dmodel of taper leaf spring

3 仿真分析及模型验证

将生成的变截面板簧三维模型 （.adm文件）导入ADAMS／View界面，删除不必要的约束，删除两副板簧中的一副板簧，删除吊耳部分，对板簧两端添加衬套约束，在板簧U型安装位置处施加一垂直向上的激励力F＝3500t（t为仿真时间，F单位为N），建立变截面板簧的动力学模型，如图4所示。

设定仿真时间为5s，步长为0.01，在后处理模块中对仿真结果进行分析，得到施加的载荷与变截面弹簧变形量的关系曲线，如图5所示。由图5中计算可得，该曲线的斜率即板簧的刚度为130.5N／mm。而实车试验测试可得该板簧的刚度为133.9±10.7N／mm，可见仿真计算所得刚度值在实测结果的范围内，表明在ADAMS中基于离散Beam梁法建立的变截面板簧模型是正确的。

图4 变截面板簧动力学模型Fig.4 Dynamic model of taper leaf spring

图5 变截面板簧刚度曲线Fig.5 Stiffness curve of taper leaf spring

4 结语

本文在多体动力学软件ADAMS中建立了基于离散Beam梁法的变截面钢板弹簧的动力学模型，并将仿真计算得的刚度值与试验测试结果进行对比分析，验证了该模型的正确性。

［1］朱晓博.少片变截面钢板弹簧结构设计与性能研究［D］.武汉：武汉理工大学，2011.

［2］王庆五.渐变刚度钢板弹簧设计研究［D］.昆明：昆明理工大学，2003.

［3］丁华，肖廉明，朱茂桃.少片钢板弹簧力学特性有限元分析［J］.汽车工程，2009，31（9）：864－866，819.

［4］景立新，郭孔辉，卢荡.钢板弹簧三连杆模型参数辨识研究［J］.汽车技术，2010（12）：10－13，54.

［5］Sugiyama H，Shabana A A，Omar M A，et a1.Development of nonlinear elastic leaf spring model for multibody vehicle systems［J］.Computer Methods in Applied Mechanics and Engineering，2006，195（50－51）：6925－6941.

［6］黄建，王良模，彭曙兮，等.基于多体动力学的钢板弹簧建模方法研究［J］.汽车技术，2011（8）：10－13.