和声搜索评定深孔轴线直线度误差的研究*
2015-11-04李少敏于大国王继明郝永鹏
李少敏,于大国,王继明,郝永鹏
(中北大学a.机械与动力工程学院;b.山西省深孔加工工程技术研究中心,太原 030051)
和声搜索评定深孔轴线直线度误差的研究*
李少敏a,b,于大国a,b,王继明a,b,郝永鹏a,b
(中北大学a.机械与动力工程学院;b.山西省深孔加工工程技术研究中心,太原 030051)
针对直线度误差评定方法中评定基线难以确定的现状,提出和声搜索评定深孔轴线直线度误差的方法;以形状位置公差评定的最小条件原则为基础,以任意方向直线度误差评定的最小包容区域法为检测模型,将和声搜索算法与评定基线寻优相结合;分析了和声搜索算法的操作原理,将和声记忆库中每行的信息对应一条评定基线,通过和声记忆库的更新搜索最优评定基线;经检验和声搜索评定方法可行,根据MATLAB计算结果分析和声搜索算法能够提高直线度误差评定精度,可以为任意方向直线度误差的评定提供参考。
和声搜索;直线度误差;评定基线
0 引言
孔径比大于5的孔被称为深孔[1-2]。由于直线度误差对深孔零件工作状态影响较大,所以深孔轴线直线度误差的检测在深孔加工检测环节占有重要地位。国家标准GB/T11336-2004提供了三种直线度误差的检测方法即两端点连线法、最小二乘法和最小包容区域法[3]。深孔直线度误差检测的难点主要集中于两个方面:如何准确地获取评定对象的空间位置信息,即以深孔轴线作为评定对象时,如何准确地获取深孔轴线的空间坐标信息;如何找到符合最小条件原则的评定基线。在直线度误差评定的三种方法中最小包容区域法符合最小条件原则,评定原理科学,但由于该方法评定基线的确定方式复杂,故其应用有限。目前多采用两端点连线法及最小二乘法评定直线度误差,上述两种方法的原理性误差较大。基于以上问题研究人员提出了智能算法、切比雪夫逼近、误差分离、坐标变换及改进的LSM等算法求解任意方向直线度误差[4-10]。然而这些方法的切入点与形状误差评定的最小条件并不完全吻合,方法本身是在以误差结果为向导进行接近,忽视了直线度误差评定中最优评定基线的确定。
和声搜索算法是对音乐家调整各种乐器的演奏曲谱的创作过程的模拟。Zong Woo Geem将创作过程用数学方式表达出来,在2001年提出和声搜索算法[11]。将直线度误差评定基线的寻优与和声算法相结合,达到或接近全局最优解,提高深孔轴线直线度误差检测方案的可靠性及检测精度。
1 和声搜索算法原理
和声是音乐创作中将多个音符在同一时间的组合体现。恰当的和声编排能够给人带来听觉上的冲击。和声搜索的原理如下:
和声乐理:在乐理知识中同时发出3个符合条件的音符构成一组和弦,以此为依据,现在有3种不同的乐器,每种乐器能够发出Do、Re、Mi、Fa、Sol、La、Si七个不同的音高,每种乐器可以同时发出不同的音符,当发出的音符符合乐理规则时得到美妙的和声。数学描述:三种乐器分别代表三种自变量xi、yi、zi,和声为函数f(xi,yi,zi),自变量的取值范围为:

A代表Do、Re、Mi、Fa、Sol、La、Si,将其数值代换,分别用7个阿拉伯数字表示,则有:
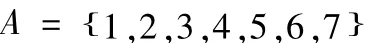
如以小三和弦2(Re)、4(Fa)、6(La)组成的音作为和声目标值,求解和声如图1所示,得到矩阵的每一行都是一个最优解。
和声搜索模拟上述过程进行寻优操作,算法与最优化问题的对比关系如表1所示。

表1 和声练习与和声搜索对比
和声算法初始化和声记忆库后从中随机产生新的和声,然后以新和声与记忆库中最差的和声对比,若新和声相对优则放入和声记忆库,最差和声从记忆库删除,循环至满足停止准则,和声搜索算法的基本步骤为[12-13]:
步骤1:初始化优化问题和算法参数;
步骤2:初始化和声记忆库(HM);
步骤3:新和声的创作;
步骤4:更新HM;
步骤5:重复步骤3、4至终止。
在步骤1中初始化优化问题:

初始化主要参数有:和声记忆库规模HMS,即和声记忆库的大小;和声库取值概率HMCR,其含义为即兴演奏中从HM中取值的概率,HMCR的概率取值范围为 [0,1],即HMCR为P时,从HM中取值的概率为P,随机取值的概率为1-P;音调调整率PAR;距离带宽BW;终止条件。
步骤2初始化和声记忆库即HMS个和声存储,矩阵中每一行代表一个解,矩阵表示如下:

步骤3新的和声描述为:

新和声的产生有三种方式:①和声记忆库中学习获取;②音调微调获取;③即兴创作获取。
首先生成[0,1]之间均匀分布随机数rand,操作公式为:
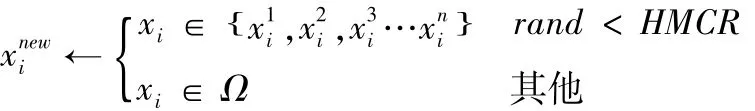
上式中Ω为随机产生新和声的取值空间。和声记忆库取出和声后有PAR的概率会有微调,微调公式为:

将新的和声与和声记忆库中最差的和声比较,更新和声记忆库。
2 深孔轴线直线度误差的评定
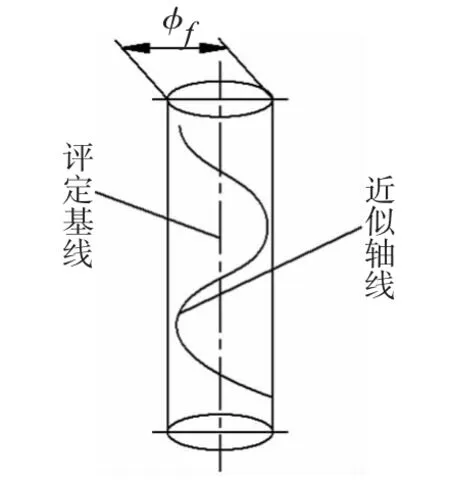
图2 最小包容区域圆柱面
深孔轴线离散点的集合为O:
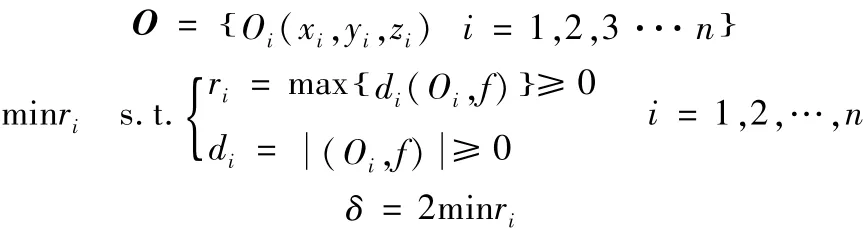
di-轴线上点到评定基线的距离
f-评定基线
Oi-近似轴线上离散点的信息
δ-深孔直线度误差
和声搜索评定深孔直线度误差描述:
(1)初始化优化问题和算法参数
目标函数为min ri,且有如下条件:
本文给出了一种基于能量均衡树的无线传感器网络实现方案,实现了低实施成本、低维护量、高自动化的数据远程监测。利用无线传感器网络的分布式特点,大幅度提高了系统在移动性、便捷性、组网灵活性等方面的综合功能,在各个领域的应用会有很好的发展前景。

其中n为检测到的孔轴线上离散点的个数,PAR取0.5,HMCR取0.95,由于误差波动在微米级别,扰动应维持在微米级,故BW取0.01。
(2)初始化和声记忆库
深孔轴线直线度误差评定常见方法有两端点连线法及最小二乘法,其中最小二乘法确定的评定基线较两端点连线法误差小。最小二乘法以残差和最小作为基线的判定标准,以其评定的直线度误差值在微米级别波动,故可以断定最优评定基线必然在最小二乘法基线附近。故寻优范围锁定在最小二乘基线附近,最小二乘基线计算如下[14]:

已知空间直线的方向向量及直线上一点可以得到该直线方程。将测得的孔轴线上的n个点两两组合,每一组点作为一个最优解,两个点作为一行,每一行的前三个数为一个点的xyz坐标,后三个数为一个点的xyz坐标,然后在和声记忆库中第一行加入最小二乘法求得的基准直线上的两点,和声记忆库中每一行的两个空间点坐标信息可以确定一条直线,在库中存在的直线为可能的最优评定基线,和声记忆库如下:
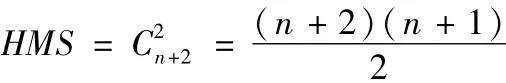

(3)新和声的创作

新和声创作的本质为新的评定基线的寻找,每进行一次创作,会产生一组新的数,即空间两个点的信息,依据空间两点的坐标可以确定一条直线。新和声由和声库中选取时,新和声分量中每一项xni可以在和声记忆库的第n列任取一个数,如图3所示。上述Ω取值表示取第n列的平均值,rand>HMCR时有:

(4)更新HM
和声记忆库更新之前对和声记忆库内的和声进行评优排序,依次取和声记忆库中第k行,求解该行代表的空间直线方程:


图3 新和声在和声记忆库中选择
(5)终止条件
终止条件一般为达到迭代次数,搜索时间及达到规定精度。为实现误差评定的确切精度,近似轴线离散点到最小二乘法确定的评定基线的最大距离为。和声库中的最小距离与的比值ξ≥20%停止搜索。
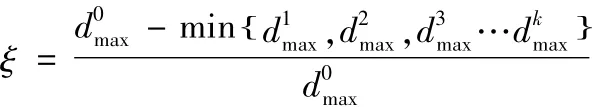
算法流程图如图4所示。
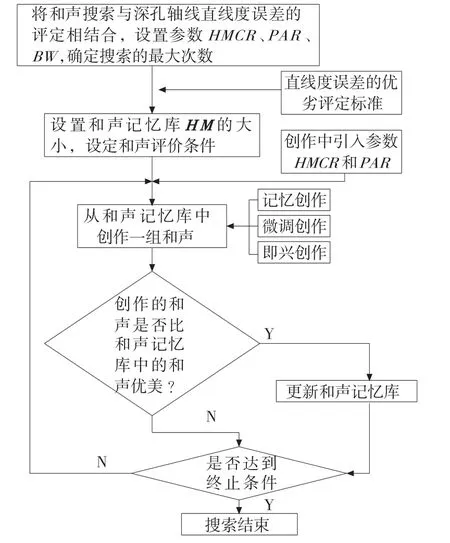
图4 和声搜索算法流程图
3 应用实例及分析
由于深孔轴线直线度误差的评定算法较少,实例采用文献[4]的原始数据进行分析,文献[4]基于遗传算法评定了任意方向直线度误差,该组数据不同算法的计算结果如图5所示[4,10,16-17]。
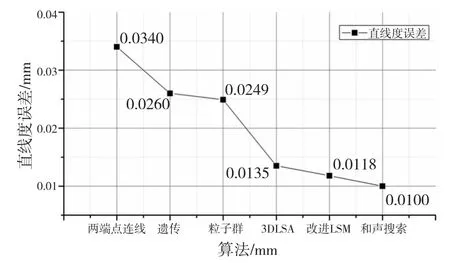
图5 文献[4]数据各算法值对比
为进一步验证算法,针对不同文献的数据及其计算方法与和声搜索算法进行对比,计算结果如表2所示。

表2 和声搜索算法计算结果 (单位:mm)
经分析可知和声搜索算法相对深孔直线度误差评定中常使用的最小二乘法有显著优势。相较于两端点连线法、遗传算法、粒子群算法及改进的LSM算法,和声算法的求解精度较高,利用和声搜索算法评定直线度误差相较其他方法评定精度有一定的提高。
4 结束语
在综合分析深孔直线度误差评定方法及和声搜索的基本原理基础上提出了一种评定深孔直线度误差的新方法,经实验验证表明:
(1)算法通用性较好,原理简单,参数少,对研究对象的要求低,方法本身很强的全局收敛性,在操作中易于实现;
(2)利用和声搜索寻优评定基线,直接从深孔零件直线度误差评定的重点切入,在原理上符合最小条件原则,评定原理更为科学;
(3)和声算法基于邻域进行搜索,深孔轴线上离散点信息在最优解周围波动,有利于最优解的求取;
(4)和声记忆库可以将评定基线转化为点坐标信息进行储存,使深孔轴线直线度误差的求解更加直接,将和声搜索与深孔直线度误差评定相结合便于计算机进行数据处理,有较高的应用价值。
[1]王峻.现代深孔加工技术[M].哈尔滨:哈尔滨工业大学出版社,2005.
[2]王世清.深孔加工技术[M].西安:西北工业大学出版社,2003.
[3]GB/T1136-2004.直线度误差检测[S].北京:中国标准出版社,2004.
[4]廖平,喻寿益.基于遗传算法的空间直线度误差的求解[J].中南工业大学学报,1998,29(6):76-78.
[5]罗钧,王强,付丽.改进蜂群算法在平面度误差评定中的应用[J].光学精密工程,2012,20(2):422-430.
[6]尹自强,李圣怡,王卓.直线度的高精度测量[J].计算机测量与控制,2004,12(2):110-113.
[7]黄富贵,崔长彩.任意方向上直线度误差的评定新方法[J].机械工程学报,2008,44(7):221-224.
[8]胡仲勋,王伏林,周海萍.空间直线度误差评定的新算法[J].机械科学与技术,2008,27(7):879-882.
[9]刘承雨,李郝林.基于坐标变换原理的空间直线度误差评定[J].现代制造工程,2013(3):94-96.
[10]胡仲勋,杨旭静,金湘中.LSM算法评定空间直线度误差的分析与改进[J].湖南大学学报(自然科学版),2010,37(2):27-31.
[11]Lee K S,Geem ZW.A new meta-heuristic algorithm for continuous engineering optimization:harmony search theory and practice[J].Computer methods in applied mechanics and engineering,2005,194(36):3902-3933.
[12]Geem ZW,Tseng C L,Park Y.Harmony search for generalized orienteering problem:best touring in china[A]// Advances in natural computation[C].Berlin Heidelberg:Springer,2005.
[13]王炳杰,赵军鹏,王春洁.基于三维最小二乘方法的空间直线度误差评定[J].北京航空航天大学学报,2014,40(10):1477-1480.
[14]于大国,宁磊,孟晓华.基于最小二乘法深孔轴线直线度误差评定[J].组合机床与自动化加工技术,2014(1):39-41.
[15]茅健,曹衍龙.基于粒子群算法的空间直线度误差评定[J].工程设计学报,2006,13(5):291-294.
[16]胡仲勋,杨旭静,金湘中.评定空间直线度误差的3DLSA算法研究[J].中国机械工程,2010,21(3):325-329.
(编辑 李秀敏)
Research on Harmony Search for the Evaluation of Deep Hole Axis Straightness Error
LIShao-mina,b,YU Da-guoa,b,WANG Ji-minga,b,HAO Yong-penga,b
(a.School of Mechanical and Power Engineering;b.Research Center of Deep-hole Machining Engineering Technology,North University of China,Taiyuan 030051,China)
During evaluating straightness error it is difficult to determ ine the evaluation baseline,for the status quo proposed harmony search method assessment deep hole axis straightness errors;based on m inimum zone condition to shape position tolerance assessmentprinciples,in any direction straightnesserror evaluation least envelope zonemethod as amodel,combined harmony search w ith the evaluation baseline optim ization;analysised of the harmony search algorithm theory,the information of each row in harmony memory corresponding to a baseline assessment,by updating the harmonymemory search for optimal evaluation baseline;upon exam ination harmony search assessmentmethod is feasible,based on MATLAB calculation results that harmony search algorithm could improve the accuracy of straightness error evaluation,it could provide a reference for the evaluation of straightness errors in any direction.
harmony search;straightness error;evaluation baseline
TH122;TG65
A
1001-2265(2015)07-0100-04 DOI:10.13462/j.cnki.mmtamt.2015.07.027
2015-04-03;
2015-05-02
国家自然科学基金资助项目(51175482);山西省发明专利转化项目(141004);中北大学科学基金资助项目(2012111)
李少敏(1988-),男,山西大同人,中北大学硕士研究生,研究方向为深孔加工及检测,(E-mail)lishaominmail@163.com。
