基于服役寿命的公差优化数学模型的研究*
2015-11-04程彬彬王志越黄美发吴常林孙永厚覃祖和
程彬彬,王志越,黄美发,吴常林,孙永厚,覃祖和
(1.桂林电子科技大学机电工程学院,广西桂林 541004;2.中国电子科技集团公司第四十五研究所,北京 100176)
基于服役寿命的公差优化数学模型的研究*
程彬彬1,王志越2,黄美发1,吴常林1,孙永厚1,覃祖和1
(1.桂林电子科技大学机电工程学院,广西桂林 541004;2.中国电子科技集团公司第四十五研究所,北京 100176)
传统的公差优化数学模型,一般只考虑加工成本及质量损失,很少关注公差对产品服役寿命内的经济效益的影响。基于产品退化方式给出了公差与产品服役寿命密度分布函数的关系,综合考虑产品平均服役寿命、加工成本及质量损失,提出了一种新的公差优化数学模型。通过轴套实例分析了不同的公差要求对服役寿命的影响,对比了两种模型的计算结果。结果表明,综合考虑产品服役寿命的优化模型对公差优化具有一定的工程价值。
公差优化模型;服役寿命;经济效益
0 引言
公差优化设计对于提高产品质量,降低生产成本有着重要的作用,而优化模型的建立是公差优化设计的关键步骤,国外学者围绕以成本模型作为目标函数进行优化设计已经展开了大量的研究,提出了指数模型、幂指数模型、负平方模型、指数和幂指数复合模型、线性和指数复合模型、三次多项式模型、四次多项式模型[1]等。国内学者对上述的公差成本模型的优化也进行了大量的研究[2-4]。日本学者Taguchi针对质量定义存在的问题提出利用产品质量损失描述产品质量,此后学者们对基于制造成本与质量损失的公差优化设计展开了大量的研究[5-9]。田口质量损失模型事实上是从出厂时间点估计产品对社会可能带来的损失,TERAN等基于产品退化原理并结合工程经济分析原理提出了一种对称望目质量特征的质量损失现值模型[10],进一步考虑了产品服役过程中产品质量特征值的退化,文献[11]在TERAN质量损失模型的基础上考虑特征之间的相关性提出一种改进的质量损失现值模型,文献[12]分析了TERAN提出的几种经典的退化模型并结合货币的时间价值提出一种并行公差优化设计方法。文献[13]对TERAN的质量损失模型进行改进提出了基于产品服役寿命分布的产品质量损失模型。
上述研究大多针对公差总成本(加工成本、质量损失),很少研究公差对产品服役寿命的影响,很少探讨高成本公差生产问题。本文基于退化原理的产品平均服役寿命,提出基于产品服役寿命的综合公差优化模型,最后结合实例探讨了公差对产品服役寿命的影响,计算了不同公差要求下产品的服役寿命,并将基于服役寿命的综合模型与只考虑加工成本、质量损失的模型进行了对比分析。
1 服役寿命计算
传统的质量观认为,只要产品满足设计要求就认为产品是合格的,对这些合格的产品不需要加以区分。日本学者Taguchi提出一种新的质量观,认为质量是产品投入服役后给社会带来的损失,但不包含产品本身内在的功能缺陷带来的损失,在此基础上提出用质量损失来衡量质量并提出了质量损失函数,基于望目特性的田口二次损失函数为:

式中k为加工过程中的质量损失系数,y为产品的质量特征值,m为产品质量特征y的真值。对于大批量零件生产时,产品质量特征值y在生产过程中服从正态分布,其平均质量损失函数为:
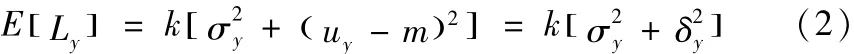
Taguchi提出的质量损失函数是在产品投入服役的时间节点上对损失进行预测估计,并没有考虑由于服役期间产品的磨损退化使质量特征值y发生变化的情况。TERAN等人基于产品在使用过程中的退化,结合工程经济分析原理提出了一种对称望目质量特征的质量损失现值模型。TERAN认为产品在服役过程中由于产品退化使得质量特征值y(t)会随时间变化,所以动态的平均质量损失函数为:
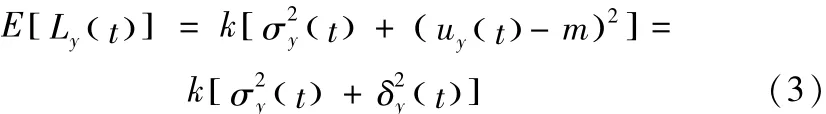
TERAN认为在产品服役过程中由于产品的使用存在各种各样产品质量退化方式,主要表现在质量特征值y()t的均值uy(t)及方差上,并提出几种典型的退化方式。产品的退化方式为:
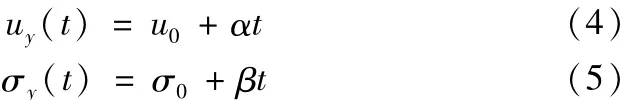
式中,u0、σ0分别表示刚投入服役时(即刚出厂时,t=0)质量特征值y的均值与标准差,主要由产品制造过程中各因素决定,如生产设备、工人技术水平等;常数α、β为产品质量退化参数,其主要由产品服役过程中各因素决定,如工作环境、润滑条件、受外力情况等。
出厂时产品的质量特征值y服从一定的随机分布,为简化研究过程假设出厂时y服从正态分布且对y值进行检测,经检验合格后才能投入使用,即产品服从截尾正态分布。则y的分布概率密度函数为:
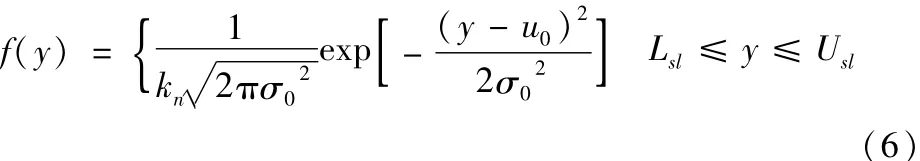
产品服役期间质量特征值y(t)也服从截尾正态分布,其分布概率密度函数为:
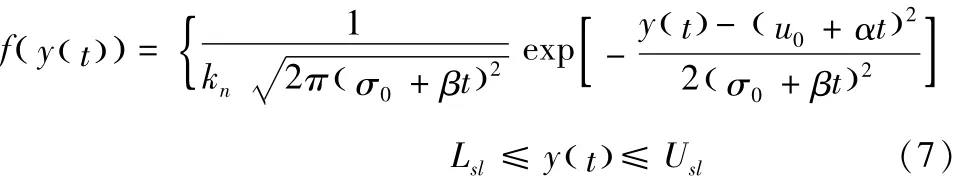
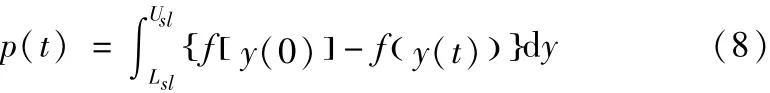
通过上式即可获得基于产品公差设计要求的产品服役寿命分布密度函数为:

则基于公差要求的产品平均服役年限为:

2 基于服役寿命的公差优化模型
一批产品投入服役后,由于受力、变形、发热、磨损和疲劳等原因,产品质量进入劣化过程,质量特征值将发生变化。如轴径将减小,孔径将变大。当产品的质量特征值超出规定的公差范围时即失效。通过上文的公式推导可知:机械产品从开始服役到失效这段时间(即产品的服役寿命)与产品的公差有关,而服役寿命的长短最终影响产品总的经济效益。因此综合研究公差对加工成本、质量损失及服役寿命的影响,对于公差的优化设计具有一定的参考价值。由式(10)可得,假设只与公差有关的产品服役寿命密度函数为ξ(t),产品平均服役寿命为N,则公差优化设计的数学模型可以用总成本与总经济效益的比值表示:
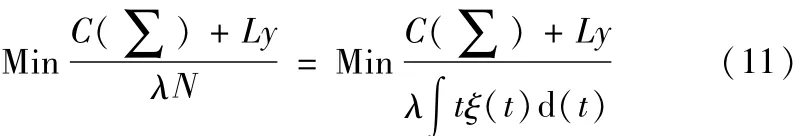
式中,λ为与产品年均经济效益有关的常数,L(y)为产品的质量损失,C(∑)为加工成本。文献[14]列出了我国中型机械类企业中等批量加工时,外圆尺寸、内孔尺寸、定位尺寸和平面尺寸的加工成本公差模型,其中内孔特征尺寸的加工成本模型为:
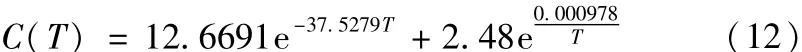
式(11)综合考虑公差对加工成本、质量损失及服役寿命的影响,较为全面的考虑了生产厂家、产品使用者及社会对产品的要求。
3 实例分析
参照文献[13]的实例,设某厂大批量生产四种基本尺寸都为φ65.0的轴套,公差要求为IT7、IT6、IT5、IT4。假设四种轴套在相同的工作环境下工作具有相同的退化方式,且退化方式为α=0.0015mm/年,β= 0.00045mm/年。为简化计算过程假设各公差带都对称分布,即Δ=T/2,u0=65.0mm。其中加工成本采用式(12),质量损失采用式(1)且偏差δy=0。分别计算不同公差要求所对应的服役寿命(年),计算结果如表1所示。

表1 不同公差要求的服役寿命
由表1可得产品公差设计要求对于产品服役寿命具有一定的影响,且随着公差等级的升高服役寿命降低。
假设该厂大批量生产基本尺寸为φ65.0的轴套,轴套公差要求为±0.02,Δ=0.02、m=65.0mm、Usl=65.02mm、Lsl=64.98mm。为探讨不同的加工精度对产品平均服役年限的影响,计算出产品特征值变动范围Δ与产品平均服役年限的关系如图1所示。从图可知随Δ的增大服役寿命也相应增大。
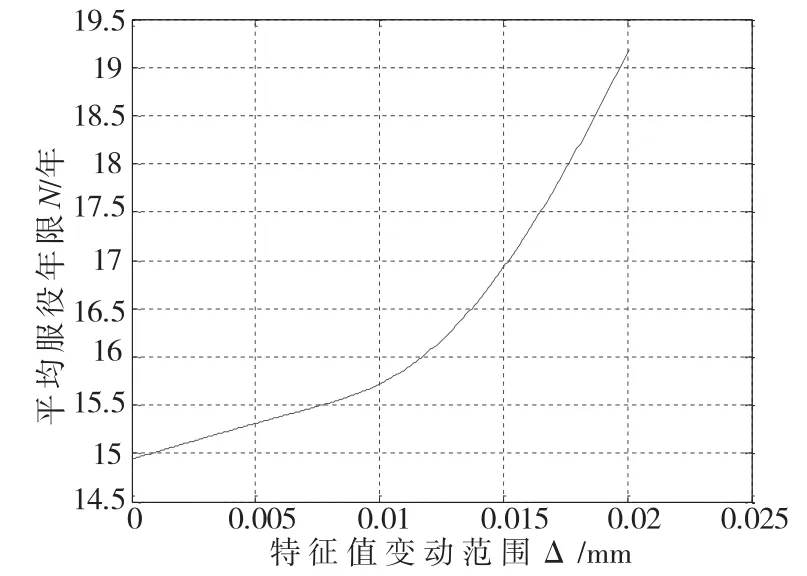
图1 特征值变动范围Δ与产品平均服役年限的关系
为了验证本文所提出模型的有效性及实用性,同时考虑计算的简便性,应用两种不同的优化模型(仅考虑加工成本、质量损失及本文提出的综合模型)按不同公差等级IT7、IT6、IT5、IT4)计算两种模型的优化结果。设轴套报废的损失取为轴套的价格Cm=150元,质量损失系数,计算参数同上。其平均寿命分别为16.93年、15.66年、15.42年、15.24年。计算结果如表2所示。表2中的计算结果表明,由于平均寿命相差不大使得基于服役寿命模型的最优方案与传统模型的最优方案相同,均为IT5,但说明本文提出的优化模型具有一定的参考价值。

表2 不同优化模型计算结果
4 总结
综合考虑了产品加工成本、质量损失及服役寿命对公差设计的影响,分析了机械产品退化原理,基于平均服役寿命内的经济效益提出了一种新的公差优化数学模型,通过轴套实例分析了不同的公差要求对服役寿命的影响,对比了不同的优化模型,结果表明,采用此模型对公差优化设计具有一定的参考价值。文中的建模方法,为改进公差优化模型提供了一定的思路,并可进一步用于公差优化分配中去。
[1]杨将新,吴昭同,顾大强.基于加工特征的成本-公差模型研究[J].工程设计,1995,3:22-24.
[2]刘玉生,吴昭同,杨将新.基于成本模型的计算机辅助公差优化设计的研究[J].浙江大学学报,1995,29(6):698-705.
[3]黄美发,高咏生.基于最低制造成本的一种公差优化设计法[J].华中科技大学学报,2002,30(4):19-21.
[4]莫帅,李振亮,李亚,等.基于资金时间价值的并行公差优化设计[J].机械设计,2011,28(11):85-88.
[5]WU C C,TANG G R.Tolerance design for products with asymmetric quality losses[J].International Journal of Production Research,1998,36(9):2529-2541.
[6]PAN J.Optimization of engineering tolerance design using revised loss functions[J].Engineering Optimization,2009,2(41):99-118.
[7]金秋,莫帅.基于改进成本公差模型的并行公差优化设计[J].天津科技大学学报,2010,25(5):53-56.
[8]张俊,杨仲春,袁方,等.基于层次分析法的公差成本优化设计[J].机床与液压,2013,41(5):66-69.
[9]彭和平,蒋向前,徐振高,等.基于多重相关特征质量损失函数的公差优化设计[J].中国机械工程,2008,19(5):590-594.
[10]TERAN A,PRATTD.B,CASE K E.Presentworth of external quality losses for symmetric nominal-is-better quality characteristics[J].The Engineering Economist,1996,42(1):39-52.
[11]PENG H P,JIANG X Q,XU Z G,et al.Optimal tolerance design for products with correlated characteristics by considering the present worth of quality loss[J].Int.J. Adv.Manuf.Technol.,2008(39):1-8.
[12]CHOU C Y,CHANG C L.Minimum-loss assembly tolerance allocation by considering product degradation and time value ofmoney[J].Int.J.Adv.Manuf.Technol.,2001,17:139-146.
[13]赵延明,刘德顺,曾磊,等.基于服役寿命分布的产品质量损失建模[J].机械工程学报,2012,48(20):182-191.
[14]方红芳,吴昭同.并行公差设计与工艺路线技术经济评价方法[J].机械工程学报,2000,36(4):74-77.
(编辑 李秀敏)
Optim ized M athematical Tolerance M odel Based on the Service Life
CHENG Bin-bin1,WANG Zhi-yue2,HUANG Mei-fa1,WU Chang-lin1,SUN Yong-hou1,QIN Zu-he1
(1.School of Mechanical and Electrical Engineering,Guilin University of Electronic and Technology,Guilin Guangxi541004,China;2.No.45 Research Institute of CETC,Beijing 100176,China)
The traditionalmathematicalmodel of tolerance optim ization,generally consider themanufacturing costand quality loss,but pay a little attention to the influence of tolerance of products econom ic benefits w ithin the service life.The relationship between tolerances and product service life distribution density function is given based on the way of product degradation.Considering the econom ic benefits of productsw ithin the average service life,manufacturing cost and quality loss,a new kind of tolerance optim ization mathematicalmodel was put forward.By example of shaft sleeve,the influence of the different tolerance requirements to service life was analyzed,the calculation results of twomodelswas compared.The results showed that the optimizationmodel of comprehensive consideration product service life has a certain engineering value on tolerance optim ization.
tolerance optimization model;service life;economic benefits
TH161;TG659
A
1001-2265(2015)07-0023-03 DOI:10.13462/j.cnki.mmtamt.2015.07.007
2014-08-26
国家自然科学基金(51365009);广西科学研究与技术开发计划项(桂科能1355012-5);广西硕士研究生科研创新项(YCSZ2014134);桂林电子科技大学研究生教育创新计划资助项目(YJCXS201501)
程彬彬(1988-),男,河南商丘人,桂林电子科技大学硕士研究生,研究方向为机电一体化技术、机电系统精度设计,(E-mail)waityouremail@126.com;黄美发(1962-),男,广西蒙山人,桂林电子科技大学教授,博士,博士生导师,研究方向为机电系统精度设计和智能测量方法。
