FDI与内资企业研发投入：基于PSM估计的实证研究

刘景章　陈震

摘要：本文使用倾向得分匹配方法，运用世界银行2005年的调查数据，通过控制代表企业特征的匹配变量构建与处理组相匹配的对照组，实证研究FDI对内资企业研发投入的影响，并比较FDI对处理组的平均处理效应。研究发现不论FDI对内资企业参与程度的高低，FDI都对研发投入有负向影响，但是这种影响并不显著。

关键词：外商直接投资；研发投入；倾向得分匹配；自主创新

中图分类号：F832 文献标识码：A

作者简介：刘景章（1971-），男，辽宁凤城人，暨南大学经济学院副教授，研究方向：经济思想史、国民经济学；陈震（1989-），男，山东烟台人，暨南大学经济学院研究生，研究方向：国外近现代市场经济理论与实践。

一、引言

20世纪90年代，中国提出了以市场换技术的战略思路，目的是通过外商直接投资（FDI）的引入，获得先进的技术、管理等，以促进经济的发展。但是本质上还是希望通过FDI的竞争、示范等效应提高国内企业的技术水平和自主创新能力，因为只有提高企业的自主创新能力，才能在残酷的市场竞争中掌握主动权。经过30多年的发展，中国经济发展取得了重大的成就，但就FDI对国内企业的创新影响效果而言，学者们并没有达成一致意见。王红领等（2006）总结了FDI与自主创新的三种观点，分别是“抑制论”、“促进论”和“双刃剑论”。但范承泽等（2008）认为这些讨论只是基于某种直观的判断，缺乏系统的理论分析和经验证据。另一个问题是学者们混淆了FDI溢出效应与FDI对自主创新的影响这两个概念，FDI溢出效应指的是FDI外部性对内资部门生产率增长或者技术进步的影响，而FDI对自主创新的影响指的是FDI对内资部门自主创新能力的影响（张海洋，2008）。本文要研究的问题就是FDI对自主创新能力的影响。在衡量自主创新能力时，有两个指标可以使用，即自主创新投入与自主创新产出。本文选用自主创新投入指标，这种做法的合理性是自主创新投入比产出更能反映企业创新努力的程度（张海洋，2008），同时研发活动可以提高自身的技术吸收和利用能力（Cohen and Levinthal，1989）。

关于FDI与自主创新的关系，国内学者提出了不少理论模型并进行了实证检验。范承泽等（2008）通过建立一个简单的理论模型分析了FDI对发展中国家企业自主研发投入的补充和替代作用，并通过实证检验发现FDI对国内企业自主科技研发的净影响为负。邢斐等（2009）在累积创新框架下通过建立一个两阶段动态博弈模型，考察了FDI对我国企业自主研发的影响，认为FDI对我国企业研发投入存在两个效应，即产品市场竞争效应以及技术溢出效应，其中产品竞争效应不确定，技术溢出效应为正。然而，他们的实证结果却显示FDI的技术溢出效应不明显。吴永求（2010）利用古诺竞争模型分析了FDI对内资企业研发支出的影响作用机制，认为其影响效果与FDI模式的成本高低有关，而实证的结果显示FDI促进了研发投入的增加。冉光和等（2013）在此基础上加入了金融发展因素，也得出了相同的实证结果，但这种影响存在区域差异。杨明等（2014）则通过研究发现，FDI技术溢出对内资企业研发投入的促进作用在生产活动中主要存在于后向关联中。

上述研究文献为本文提供了坚实的理论和实证参考。但这些文献还存在如下问题。第一，实证研究中采用多元回归方程，虽然模型中考虑了多种控制变量，但模型仍然可能遗漏某些重要变量，这就使得很难分离出导致研发投入差异的相关因素；另外，方程的内生性问题也可能导致OLS方法的估计是有偏的。尽管可以使用面板数据分析解决遗漏变量和内生性问题，但由于面板回归中使用了较多的二值定性虚拟变量，所以不能给出一致有效估计。有学者使用动态GMM方法，这是一种较好的估计方法，但在估计过程中会剔除不随时间变化的二值虚拟变量，这会由于样本的减少而导致误估。第二，大都使用基于省级或行业的面板数据对FDI与企业研发投入的关系进行研究，只有少量的文献基于微观企业数据分析，如范承泽等（2008）的研究采用了世界银行对中国公司的调查数据，但由于技术限制，虽然作者采用了Robust最小二乘法，但也难解决可能存在的内生性和选择偏误问题。

针对上述问题，本文将采用倾向得分匹配（Propensity Score Matching，PSM）方法。由于PSM估计可以不预设方程的函数形式，所以可以尽可能地避免采用非试验数据估计处理效应时的“选择性偏倚”问题，从而使估计结果更加稳健。另外，本文将运用2005年世界银行对中国12 400家制造业企业的调查数据，考察FDI对企业研发投入的影响。

二、实证设计

（一）PSM的基本思路

本文的研究目的是估计FDI对企业研发投入的影响。以企业的股权中是否有外资持有者，即是否有FDI参与，进行分类，将样本分为两组：股权中有外资占比的称为处理组（Treatment Group）；股权中无外资占比的称为对照组（Control Group）。如果直接比较FDI参与企业（处理组）与非FDI参与企业（对照组）的研发投入均值差异作为处理效应，会产生偏差（选择性偏倚），这是因为非试验数据中处理组和对照组的分配并非随机的，两组样本的参与地位以及诸多其他特征都不尽相同。换句话说，FDI与企业研发投入受样本其他特征共同影响，因此不能简单地认为企业研发投入差异仅仅是由于FDI引起的。问题在于无法观察到FDI参与企业在没有引进FDI的情况下，企业研发投入会不会也比较多，即“反事实情形”。为了解决这个问题，可以依据多个可以观测的特征量将处理组与对照组的企业进行逐一匹配。匹配后，处理组和对照组只在是否有FDI这方面保持不同，其他方面保持相同或者是相似。这样就构造了一个与FDI参股企业相匹配的“反事实情形”，各匹配个体是否接受处理就可以视为随机的，匹配对象的结果变量（本文中为企业研发投入）差异则是接受处理的效应。由于在匹配的过程中使用多个特征变量会导致匹配过程变得复杂，从而落入“维度陷阱”，因此有必要构造一个单一指标，使其包含其他特征变量的所有信息，保证匹配过程的可操作性。本文采用Rosenbaum和Rubin（1983）提出的“倾向匹配得分”（PSM）方法，将倾向得分作为唯一的匹配指标对处理组与对照组进行匹配。

（二）PSM的两个基本假定

1.条件独立假定（Conditional Independence Assumption，CIA）

假定处理组和对照组所有相关差异都可以用一系列可观测匹配变量衡量，在控制了共同影响因素以后，FDI与企业研发投入是相互独立的，可用公式表示为：

（三）PSM操作方法

相对于没有FDI时的研发投入水平，企业FDI对处理组的平均处理效应（the Average effect of Treatment on the Treated，ATT）可用下式表示：

三、实证检验与结果分析

（一）数据来源与变量选取

本文中用到的数据来自于世界银行2005年对中国12 400家制造业企业的投资环境调查。调查分层取样了120个代表性城市30个二位码行业的数据，包括针对企业管理层取样的企业基本信息和针对企业会计、人力资源经理取样的企业财务和人事信息。

本文中对企业的研发投入的衡量，以企业研发费用支出占全部产品销售收入的比重来表示，目的是为了剔除企业规模对研发投入的影响，以变量RD表示；对于企业是否有FDI参与，以企业股东中外资持有者的持股比重是否大于零来表示，并设置虚拟变量fdi，当有FDI参与时，fdi=1；否则，fdi=0。依据前文文献所述，并同时满足PSM的条件独立假定，匹配变量X包含企业滞后一期的生产率水平、企业规模、人力资本、企业年限以及企业所属地区和企业所有制形式虚拟变量。

在衡量企业的生产率水平时，虽然OP和LP方法能够较好地解决OLS可能存在的内生性问题，但是由于数据限制，本文仍然用劳动生产率来表示企业的生产率水平，以变量lnpd表示，具体以产品的年度销售收入与公司总雇佣人数之比来表示，其中销售收入为主营业务收入与其他业务收入之和。企业规模（scale）的衡量指标主要有企业产品销售收入、雇佣人数或资本存量。由于劳动生产率实质上是前两个企业规模指标之比，所以为了最大限度地利用样本数据进行估计，选用固定资产净值作为企业规模变量。人力资本（H）以完成高等教育的总雇佣人数表示，其值为总雇佣人数与完成高等教育比例之积。前述变量均取对数形式。企业年限（age）根据企业的成立时间计算得出。地区虚拟变量以中西部地区为基准，设置东部地区虚拟变量（east）。所有制形式虚拟变量dum1、dum2分别在企业所有制为国有和私营时取值为1，其他情况取值为0，其中国有形式包括调查中的国有（SOE）、集体（Collective-owned）等两种形式；私营形式包括股份合作（Share joint-owned units）、股份有限（Limited liability corporation）、联营（Shareholding corporation）、私营（private-owned）等四种形式。

由于样本中存在异常值，所以在进行匹配平衡性检验之前要对数据进行清洗，剔除如固定资产净值、主营业务收入小于等于零和其他业务收入小于零的样本值以及企业成立时间异常的样本。另外，由于本文考查的是FDI对内资企业研发投入的影响，所以去除所有制形式为外资的样本，包括港澳台投资与外商投资。对于外商股权比例为100%，而又未登记为外资的样本，也予以剔除。经过数据筛选以后，保留9 919家样本数据。

（二）实证检验

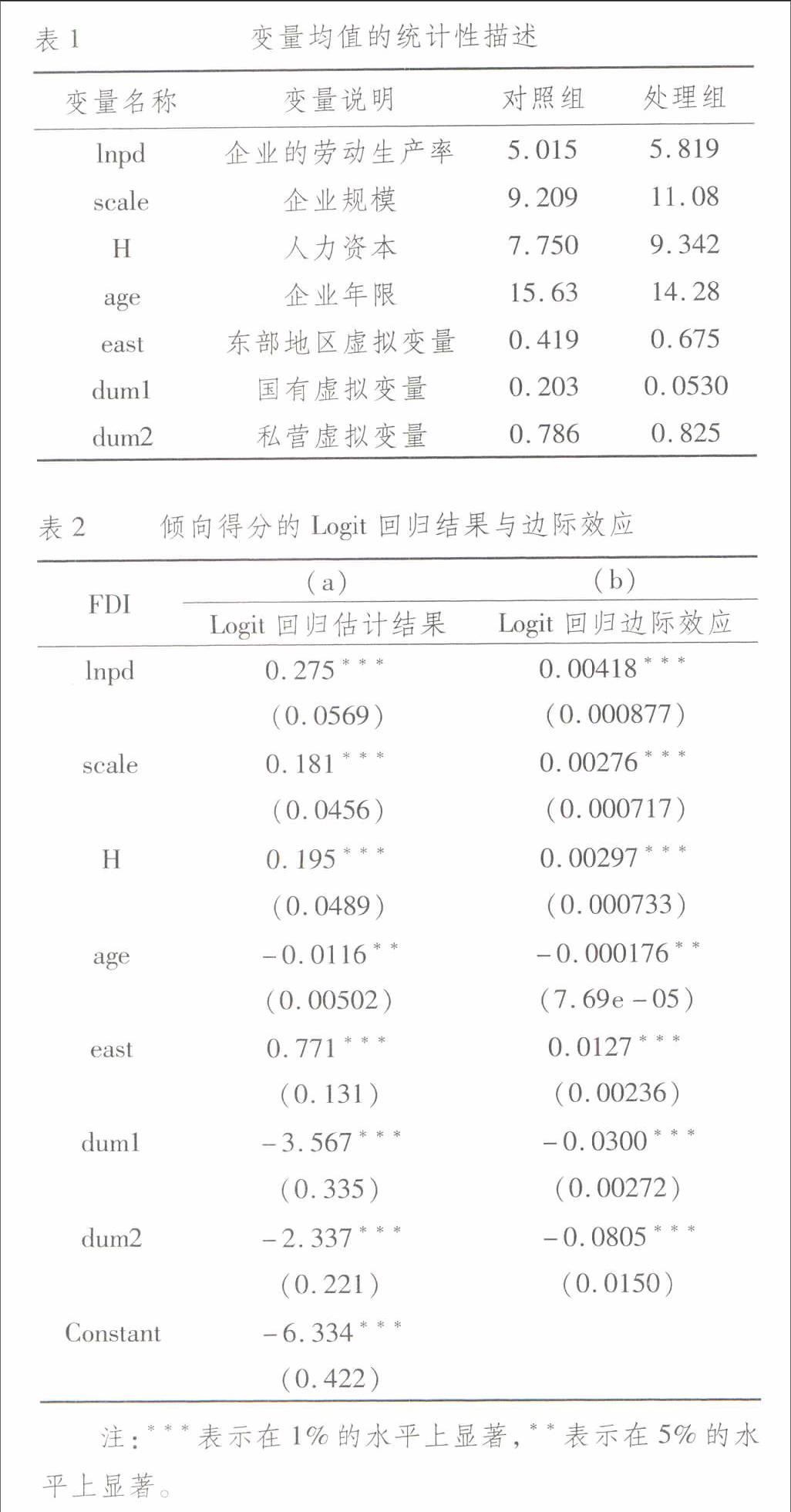
首先，使用Logit模型估计倾向得分，即在控制匹配变量X的情况下，估计样本企业中有FDI的概率预测值。表2中第（a）列用来判断匹配变量对FDI的影响方向，其中劳动生产率、规模、人力资本和东部地区虚拟变量都对FDI有正的影响，说明劳动生产率高、规模大并且有人力资本优势的企业更容易获得FDI；相反，企业年限和所有制虚拟变量都对FDI有反向影响，可能的原因是年限长的企业会因为管理、技术方面成熟而不需要通过对FDI的引进实现自身增长和技术进步。第（b）列为各变量对FDI影响的边际效应，可以更直观地读出变量变动对FDI大小的影响，其中劳动生产率每提高1%，将使FDI增加0.004%。

从图1中可以看出，处理组的核密度最高值位于对照组的最高值的右侧，处理组的总体分布偏右，而对照组的总体偏左。在核密度较低、倾向得分较高的部分，处理组和对照组有较大的重合。

在测得倾向得分以后，就可以进行样本匹配。使用PSM估计FDI对研发投入的处理效应时，有一个前提条件就是：有无FDI参与不再取决于各匹配变量，也就是要满足条件独立假定。可以通过检验各个匹配变量在FDI企业与非FDI企业间分布差异或者平衡性检验来判断其是否成立。本文主要依据Smith和Todd（2005）的方法，通过计算配对后处理组企业与对照组企业基于各匹配变量的标准偏差（Standardized Bias）进行匹配平衡性检验。处理组与对照组基于匹配变量X的标准偏差为：

标准偏差的值越小则模型匹配效果越好，只要标准偏差的绝对值小于20%就不会引起匹配的失效。由于表2中各匹配变量的显著性水平较好，可以对FDI概率有较为准确的预测，且由图1可以看出对照组样本主要集中于低倾向得分区域，使用核匹配反而会因为使用过多的低倾向得分样本而使匹配失效，所以本文采用最近邻一对一匹配方法。表3给出了各个匹配变量的平衡性检验结果。

从表3中可以看出，首先各匹配变量的标准偏差绝对值都小于20%，说明匹配过程有效；其次，各匹配变量的T检验p值都大于0.1，即各匹配变量的差异都在10%的水平上不显著，说明经过匹配以后，各变量之间不存在显著的组间差异。以上两点都表明匹配过程满足倾向得分匹配的基本假定，保证了匹配的有效性。图2给出了匹配以后处理组与对照组倾向得分的核密度图。从图2可以看出，处理组与对照组几乎完全重合，进一步说明了匹配过程的有效性。

本文以FDI参与企业的股权占比中位数，将处理组企业分为两组：FDI高参与度企业和FDI低参与度企业。两组都以无FDI参与企业作为对照组实施倾向得分匹配过程。两组估计结果及总体估计结果见表4。

从表4可以看出，经过匹配以后，总体样本的ATT仍然在10%的显著性水平下不明显，但是经过匹配以后，ATT的方向发生了变化。将总体样本分为FDI高参与度与低参与度两个子样本之后，ATT的方向都如总体样本一样发生了改变，即FDI对研发投入可能存在负向影响，而不是原来的正向影响。分组之后，T检验的p值变大，说明总体样本的显著性水平不明显与FDI的参与程度无关。但是在综合了两组子样本之后，总体样本的T检验p值减少，说明可能随着样本数的增加会使T检验的显著性增加，在以后的研究中可以使用更大的样本来改进本文的结论。

四、结论

本文运用世界银行2005年对中国12 400家制造业行业的企业调查数据，基于倾向得分匹配方法，实证分析了FDI对内资企业研发投入的影响。通过构造与处理相匹配的对照组，可以在一定程度上减少样本的选择性偏倚。在控制了企业的匹配变量以后，再考察FDI对研发投入的影响发现，FDI对内资企业的参与度不论高低，都对研发投入的影响为负，这与范承泽等（2008）的研究一致。虽然这种影响并不明显，但随着样本数据的增大，其p值有变小的趋势，将来可以在研究中纳入更多的FDI企业数据来扩展本文。

从本文的研究结论可以看出，不能过分迷信FDI给企业带来的创新影响，过多的引入FDI并不能从本质上提高企业的创新能力，反而可能由于FDI的进入，对内资企业产生冲击，从而减少研发投入，使内资渐渐丧失自主创新能力。因此，应鼓励内资企业的自主创新，加大对企业创新的扶持，而不是寄希望于FDI。

参考文献：

[1] 王红领，李稻葵，冯俊新. FDI与自主研发：基于行业数据的经验研究[J].经济研究，2006（2）：44-56.

[2] 范承泽，胡一帆，郑红亮.FDI对国内企业技术创新影响的理论与实证研究[J].经济研究，2008（1）：89-102.

[3] 张海洋. 外国直接投资对我国工业自主创新能力的影响——兼论自主创新的决定因素[J].国际贸易问题，2008（1）：72-81.

[4] COHEN W M， LEVINTHAL D A. Innovation and learning： the two faces of R&D[J].Economic Journal， 1989，99（397）：568-596.

[5] 邢斐，张建华.外商技术转移对我国自主研发的影响[J].经济研究，2009（6）：94-104.

[6] 吴永求. FDI对国内企业研发行为的影响——理论模型与中国的经验[J].世界经济研究，2010（1）：82-86.

[7] 冉光和，张冰，庞新军.金融发展、外商直接投资与企业研发投入——基于我国省级面板数据的实证研究[J].经济经纬，2013（2）：121-126.

[8] 杨明，李春艳.FDI对内资企业R&D投入的影响机制研究[J].甘肃理论学刊，2014（1）：152-156.

[9] ROSENBAUM P， RUBIN D. The central role of the propensity score in observation studies for causal effect [J]. Biometrika， 1983， 70（1）：41-55.

[10]SMITH J， TODD P. Does matching overcome Lalonde′s critique of nonexperimental estimators？[J].Journal of Econometrics， 2005， 125（1-2）：305-353.

（责任编辑：张曦）