基于锥形电极的三维型腔精确加工方法研究

王志良，郑博文，庄晓舜，周兆威，裴景玉

（上海交通大学机械与动力工程学院，上海200240）

基于锥形电极的三维型腔精确加工方法研究

王志良，郑博文，庄晓舜，周兆威，裴景玉

（上海交通大学机械与动力工程学院，上海200240）

提出并分析了在利用圆锥形电极定长补偿方法分层加工三维型腔实验时，其第一层第二道加工切除残余突起后形成的实际加工深度与理论分层厚度的差异，该差异存在于加工时采用的关键加工参数补偿长度的误差。进而探究并提出了精确计算第二道加工时补偿长度的方法，并通过实验验证了该补偿长度的准确性，从而使第一层两道加工后形成的加工深度达到理论值。最后，利用该方法进行两层的三维型腔加工实验，由此证明型腔加工效果良好，满足型腔尺寸及形状精度的要求。

电火花铣削加工；三维型腔加工；锥形电极；定长补偿；锯齿面

复杂形状成形电极的设计与制造是电火花成形加工缺乏加工柔性的一个重要原因；且由于电火花加工过程中不可避免的电极损耗现象，决定了用同一电极完成高精度型腔粗、精加工全过程的不现实性［1-2］。因此，自20世纪80年代后，国内外众多学者纷纷开始尝试使用形状简单的电极（如棒状电极），将复杂型腔的加工分成很多等厚度的单层问题，借鉴数控铣削的方法进行三维轮廓的电火花加工［3-5］。由于在加工中采用标准电极，省去了成形电极的设计和制造过程，从而能简化工艺流程、节省加工成本［6］。同时，由于采用形状简单的电极进行数控电火花铣削加工，将有利于减小电火花加工中面积效应和电容效应的影响，从而大大提高了复杂型腔的加工稳定性和加工质量［7］。这种方法成为目前普遍采用的微细电火花三维型腔加工方法。

国内外学者针对电火花铣削加工方法进行了大量的研究。余祖元等［8-9］率先提出了均匀损耗方法，并利用CAD/CAM系统加工出了复杂的三维型腔；李剑忠等［10］在均匀补偿的基础上提出了均匀损耗分段补偿方法，并对三维型腔进行加工，提高了加工效率和精度。上述研究建立在均匀损耗方法之上，虽能使电极保持初始形状，但由于必须控制分层加工厚度小于放电间隙，导致加工效率极低。裴景玉等［11］针对电火花铣削加工提出了定长补偿方法；郑博文等［12］在此基础上进一步研究并提出圆锥形电极的定长补偿方法，并通过实验验证了圆锥形电极铣削加工数学模型的准确性，以及定长补偿加工截面轮廓具有很好的稳定性。然而，上述研究的理论模型缺乏精确的补偿长度计算方法，导致型腔底面形状及尺寸精度并不是很好。何磊等［13］针对电火花锥形电极定长补偿过程中锥形电极的形成过程及其锥形保持的稳定性进行了实验研究。

本文基于圆锥形电极的定长补偿方法，着重研究了圆锥型电极三维型腔第一层精确加工的实现方法；同时，在此基础上建立了型腔第二层加工时波浪面作为原始面的数学模型，并进行了仿真；最后，通过实验验证了该方法能高效精确地得到型腔底面，为微细三维型腔精确加工提供了理论参考。

1 方法的提出及仿真分析

1.1 锥形电极下的定长补偿算法

如图1所示，在电火花铣削过程中，电极不断损耗，导致加工型腔底面达不到平面精度要求。为保证加工平面精度，当电极损耗达到设定值le时，补偿一次，补偿量为le，此为补偿精度；对于确定的补偿精度，可经过计算得到对应的加工长度L，称为补偿长度。这种每隔一个固定的加工长度L，电极轴向补偿固定的补偿量le，以提高加工平面精度的补偿方法就称为定长补偿方法。

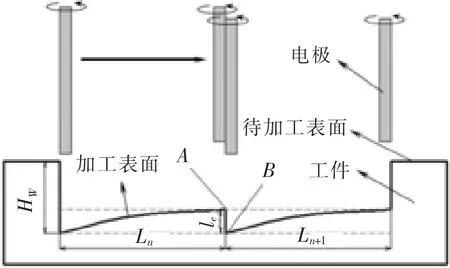
图1 定长补偿方法示意图

利用定长补偿方法，再配合电极旋转，由于在加工过程中，电极有径向规划轨迹的进给，同时又有轴向的补偿，使电极端面逐渐变得锐利。在达到稳定工作状态后，电极端面将形成一个倒置的圆锥形（图2），图2所示的各个参数有如下关系:

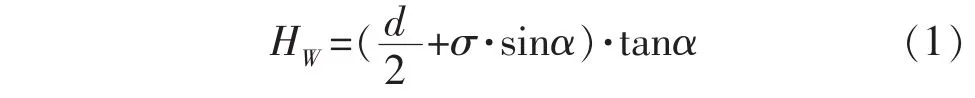
式中:HW为分层加工深度；α为电极锥形特征角；d为工具电极直径；σ为放电间隙。

1.2 定长补偿单道槽加工结果及分析

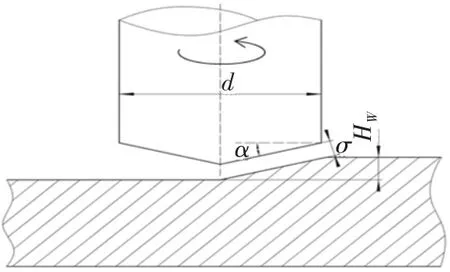
图2 锥形电极铣削加工示意图

利用锥形电极定长补偿方法分层加工三维型腔，锥形电极所走过的每一道加工轨迹形成的加工截面为一个类似倒三角形，且该方法能得到稳定的加工轮廓。图3是利用锥形电极加工单道槽的三维形貌图。可看出，槽截面为类似倒三角形，且形貌稳定。初步验证了采用定长补偿锥形电极加工方法能得到形状精度良好的槽。

图3 锥形电极单道槽三维形貌图

利用该方法，采用无轨迹重叠加工方法分层加工可得到如图4所示的型腔第一层。然而，想要加工形状精度良好，且尺寸达到精度要求的微型槽，还需进行以下几个步骤:首先，去除上一步加工留下的锥形残留；接着，采用分层加工方法进行多次铣削加工，直至尺寸达到要求。在每一层加工时，要分为两步加工:第一步，采用定长补偿方法加工出单道锥形槽；第二步，去除残留锥形突起。而按照定长补偿方法，理论上每一层的加工都是上一层相同参数重复加工的叠加。因此，上一层加工后的分层加工深度会对这一层的加工方法及加工结果产生很大的影响。因此，有必要探究第一层第二步加工深度的影响因素，以及如何才能得到一个较好的加工深度，从而使下一层加工更精确。

图4 第一层无轨迹重叠加工图

在电火花加工中，体积相对损耗比θ用来衡量电极耐损耗程度，是一个很重要的参数，即:

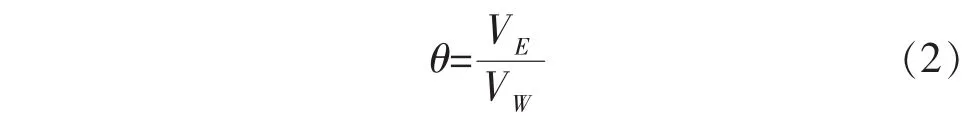
式中:VE为加工过程中电极的体积损耗；VW为工件被加工体积。一般认为，在选定了电极、工件材料及加工参数后，电极体积相对损耗比是一个常数，不会随着加工过程的进行而发生改变。由相对体积损耗比结合锥形电极横截面为三角形的特征，可得到锥形电极定长补偿算法:

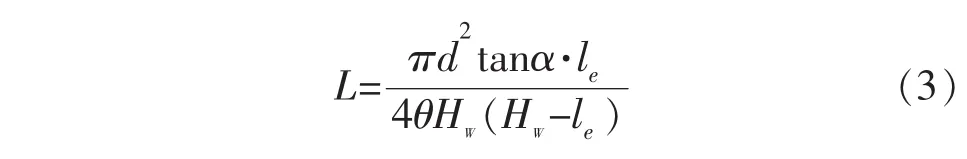
式中:L为补偿长度；d为工具电极直径；α为电极锥形特征角；le为补偿精度；θ为体积相对损耗比；HW为分层铣削深度。

由式（3）可看出，定长补偿长度L在锥形电极定长补偿法加工中是一个关键加工参数，L值的精度直接决定了加工型腔深度HW的值。同时，在实际加工实验时发现，当采用和第一步相同的补偿长度进行加工时，由于加工面变为非平面，且在加工过程中电极发生损耗，这些原因将导致分层铣削深度达不到预期深度值，即第一层第二步加工的补偿长度与第一步的长度值不同。因此，有必要研究精确加工至预期深度值时补偿长度的计算方法。

1.3 补偿长度精确计算方法

由于式（2）表示整个加工过程中电极损耗的总体积与工件被去除的总体积的比值，同时，当锥形电极定长补偿加工至稳定状态时，加工槽截面形状具有稳定性，整个加工过程就可看作是多个补偿长度内相同加工过程的叠加，故体积相对损耗比可表示为:在一个补偿长度内，电极的体积损耗与工件被去除体积的比值，从而可得到:

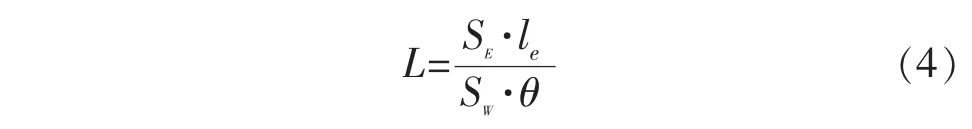
式中:L为加工补偿长度；SE为电极横截面积；SW为工件上铣削加工槽的横截面积；le为电极沿加工方向且加工长度为L时的电极损耗量。

采用CSM700共聚焦显微镜测量得到的加工截面见图5。该仪器的最大测量范围为15mm，最小步进单位为10 nm；且采用线扫描方式，成像速度高，能展现被测试件表面的真实三维形貌。图中，三角形虚线区域内为残余突起的截面图。铣削加工第二步的目标是使加工后的深度与预期分层深度相吻合，即在第二步铣削加工时需去除该区域内全部体积。理论上，已知实际加工深度及加工锥角，就可计算出该区域的截面面积SW值，从而利用式（4）得到新的更精确的补偿长度值。

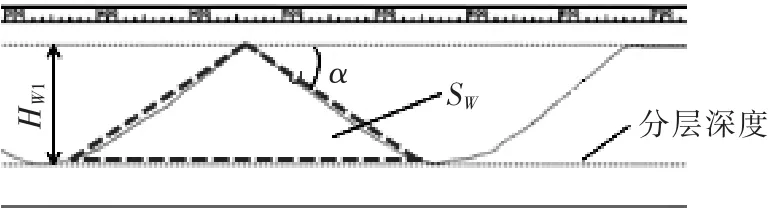
图5 第一步加工后的截面图

式（4）中，SE、le及θ为已知量。为计算截面面积SW，需知道第一步加工后的实际深度HW1，然而，加工后的实际深度和理论上的分层厚度因为电极轴向损耗的原因而不相等。因此，为得到更精确的补偿长度值，需得到实际的加工深度，可通过插值法求得。首先建立补偿长度L与实际加工深度之间的关系，表1是不同补偿长度下的实际加工深度。

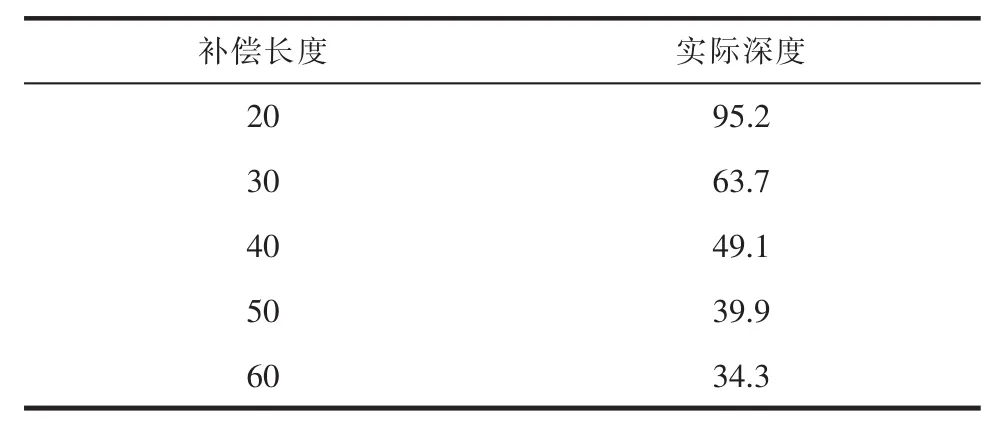
表1 不同补偿长度下的实际加工深度μm

图6是利用样条曲线拟合的实际加工深度与补偿长度L之间的关系曲线。可看出，实际加工深度随补偿长度L的增大而变小，且该变化趋势随着补偿长度L的增大而变弱。这里用样条曲线能得到二阶导数连续的样条函数，从而得到平滑的实际深度与补偿长度L之间的关系拟合曲线。

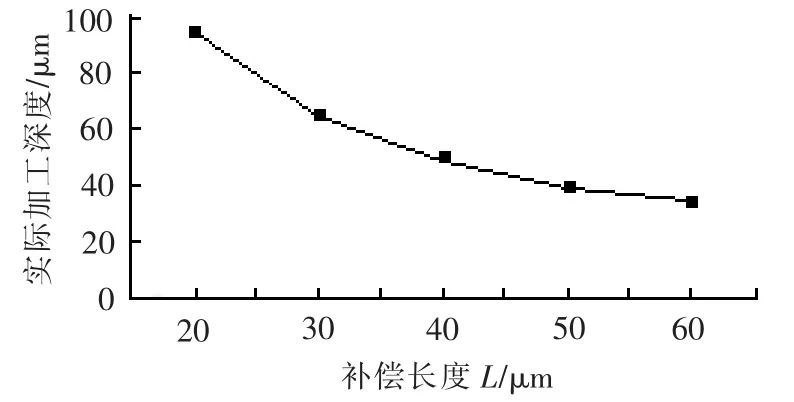
图6 不同补偿长度下实际加工深度的拟合曲线

为验证曲线的准确性，取补偿长度L为24 μm，进行单道铣削加工，得到的加工深度经测量为79.98μm。在拟合曲线上取补偿长度L为24 μm，此时在拟合曲线上获得的加工深度为79.28μm，与实际值基本吻合，说明拟合曲线是准确的。由此可得到实际的加工深度HW1，计算出截面面积SW，再根据式（4）精确计算出第二步的补偿长度L，进而对型腔进行铣削加工。

2 实验验证及结果

为验证上述方法的正确性，采用ROBOFORM 35型四轴联动电火花机床和3R旋转轴组件进行电火花加工三维型腔实验。实验仪器和材料见表2。

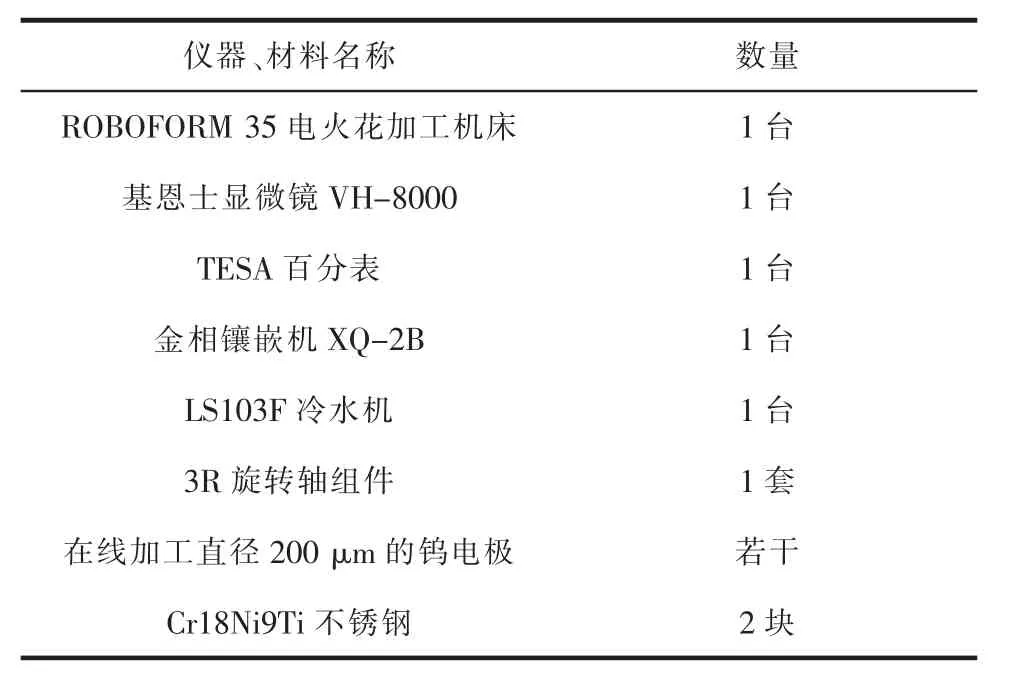
表2 实验仪器及材料

利用锥形电极并采用定长补偿方法加工型腔，每一层的加工分为两步，层与层之间采用变换加工方向的方法进行过渡。预加工轨迹是沿着需加工型腔的最外沿进行一圈加工，这样再进行后续的交替变向加工时，就不会出现未加工的残留部分。两步加工分别按无轨迹重叠的方式进行，会形成锯齿状的加工截面。第二步的加工选择沿着锯齿面中每个三角形突起的中间作为轨迹进行第二步的定长补偿铣削加工。第一层经过两步加工后，会形成如图7a所示的型腔；图7b是对应虚线处的实测截面图。可看出，由于加工中拟去除的部分为三角状突起的全部体积，所以第二步加工结束后，在分层深度线上下的体积也是相等的。这样就可认为利用重新计算出的补偿长度，能加工出深度达到预期分层厚度的三维型腔。

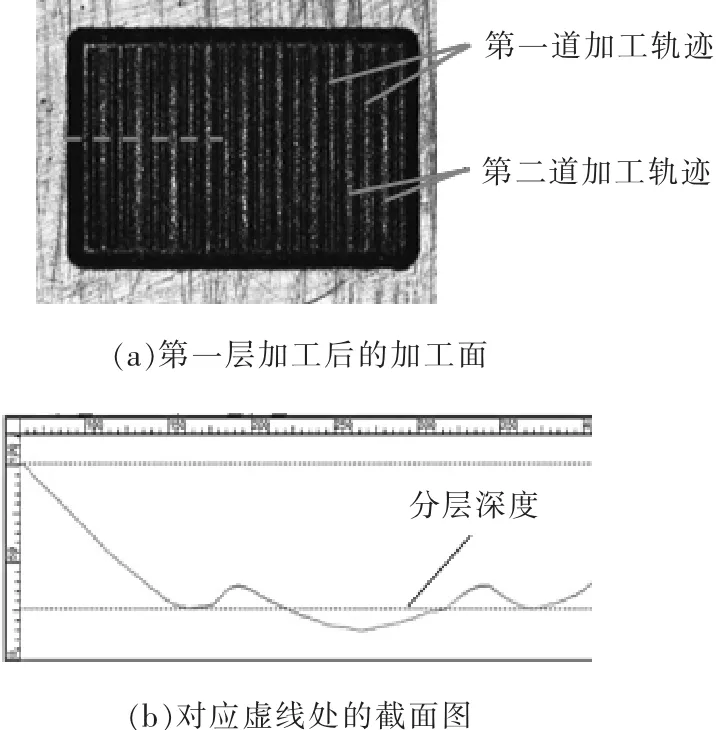
图7 第一层经两步加工后的型腔

经单道多层加工后，再进行修整加工，能得到预期深度的三维型腔。以铣削加工一个长、宽尺寸为2.1 mm×1.44 mm、型腔深度为175μm的三维型腔为例（图8a），实验中加工一个两层的型腔，每层的加工深度为80μm，加工后进行测量。图8b是加工型腔的显微照片图；图8c是图8b所示红线标记处所对应的截面轮廓曲线图。测量得到的底面非常平整，测得方形腔的加工深度为174.275μm，加工精度很好。

图8 型腔加工图

3 结语

本文针对电火花定长补偿方法加工三维型腔时，由于未能采用精确的补偿长度而导致在加工第一层第二道残切时出现加工深度不能达到理论分层厚度的问题进行了探究，并找到一种行之有效的方法，从而得到精确的新补偿长度值，保证了第二道加工的准确性，为后续多层加工提供了高效精确的加工方法。

［1］Masuzawa T.Three dimensional micromachining by machine tools［J］.Annuals of the CIRP，1997，46（2）:621-628.

［2］汤泽隆，真柄卓司，今井祥人，等.小径电极を用いた微细创成放电加工（第2报）［J］.型技术，1997，12（8）: 104-105.

［3］Masuzawa T，Fujino M，Kobayashi K.Wire electrodedischarge grinding formicro-maching［J］.Annals of the CIRP，1985，34（1）:431-434.［4］Yu Zuyua n，Kizak J，Rajurkar K P.Modelling and simulation ofmicro EDM process［J］.Annals of the CIRP，2003，52（1）:143-146.

［5］Zhao Wansheng，Yang Yang，Wang Zhenlong，et al.A CAD/CAM system for micro-ED-milling of small 3D freeform cavity［J］.Journal of Materials Processing Technology，2004，149:573-578.

［6］王振龙，赵万生，刘光壮.基于分层制造原理的微细电火花加工技术研究［J］.机械工程学报，2002（2）:22-26.

［7］王振龙，孟庆鑫，赵万生，等.分层去除微细电火花铣削加工的NC程序生成［J］.航空精密制造技术，2002，38（5）:11-12.

［8］Yu Zuyuan，Masuzawa T，Fujino M.Micro-EDM for three-dimensional cavities-development of uniform wear method［J］.Annals of the CIRP，1998，47（1）:169-172.

［9］Rajurkar K P，Yu Zuyuan.3D Micro-EDM using CAD/ CAM［J］.CIRP Annals-Manufacturing Technology，2000，49（1）:127-130.

［10］李剑忠，栾纪杰，虞慧岚，等.微细电火花三维加工中电极损耗补偿新方法［J］.大连理工大学学报，2011，51（4）:525-528.

［11］裴景玉，邓容，胡德金.微细电火花加工的底面轮廓模型及定长补偿方法［J］.上海交通大学学报，2009，43（1）:42-46.

［12］郑博文，何磊，金方进，等.圆锥形电极微细电火花铣削定长补偿方法研究［C］//第15届全国特种加工学术会议论文集.南京，2013:346-350.

［13］何磊，裴景玉，郑博文，等.定长补偿电火花铣削加工中锥形电极的形成及稳定性［J］.航空学报，2014（4）: 1165-1172.

The Study on Precise Processing M ethod of Three Dimensional Cavity Based on the Conical Electrode

Wang Zhiliang，Zheng Bowen，Zhuang Xiaoshun，Zhou Zhaowei，Pei Jingyu
（Shanghai Jiao Tong University，Shanghai 200240，China）

The difference between the actual processing depth and the theoretical depth after the second step to remove the residual parts in the first layer with conical electrode and fixed-length compensation method are put forward and analyzed.The existed difference just because of the error of compensation length when processing the residual parts in the second step.Then the precise calculation method of compensation length for the second step processing are explored and put forward.And the length of the compensation accuracy is verified by experiment，which can make the actual depth reach the theoretical value after the first layer processing.Finally，using this method，one two-layer three dimensional cavity processing experiment is done，and the experimental result shows that the processing effect is good，and canmeet the requirements of the cavity size precision and shape accuracy.

EDM milling；three dimensional cavity processing；conical electrode；fix-length compensation；serrated surface

TG661

A

1009－279X（2015）01－0007-04

2014-10-15

国家自然科学基金资助项目（51205252）

王志良，男，1987年生，硕士研究生。