MDH80加工中心铣削稳定性研究*

李泳耀，丛 明，罗孟然，李宏坤，杜黎清

（1.大连新宇理工科技开发中心有限公司，辽守大连 116024；2.大连理工大学机械工程学院，辽守大连 116023；3.一汽解放汽车有限公司无锡柴油机厂，江苏无锡 214026）

MDH80加工中心铣削稳定性研究*

李泳耀1，2，丛 明1，2，罗孟然1，2，李宏坤1，2，杜黎清3

（1.大连新宇理工科技开发中心有限公司，辽守大连 116024；2.大连理工大学机械工程学院，辽守大连 116023；3.一汽解放汽车有限公司无锡柴油机厂，江苏无锡 214026）

为了提高发动机缸体与缸盖结合面的表面加工质量，研究了铣削加工过程中的颤振稳定性问题。进行了刀具—主轴锤击模态试验和铣削力仿真实验，获得了所用刀具的低阶模态参数及铣削力系数。构建了铣削颤振的稳定性叶瓣图，用于指导切削参数的选择和优化。通过该方法可以选取合适的主轴转速和切削深度，避免加工过程中颤振的发生，提高工件表面的加工精度，并对加工刀具及机床本身有保护作用，可提高其使用寿命。

加工中心；铣削稳定性；切削颤振

0 引言

本文所研究的加工中心主要完成发动机缸体的铣面加工和孔加工，对表面质量要求较高，不允许有切削振纹产生。因此，为了获得较高的加工表面质量，切削过程中的颤振是必须要避免的。刀具的颤振稳定域分析是解决加工过程中颤振问题的有效方法。它是通过绘制轴向临界切深关于主轴转速的二维关系图，亦即稳定性叶瓣图来直观表达稳定性的切削极限。

在国外，R.S.Hahn［1］首先于1954针对磨削加工提出了振纹再生理论，Gagnol［2］等基于模态分析对高速主轴进行了颤振稳定性预测，Kivanc［3］等对端面铣削进行了结构建模，并对成形误差和稳定性进行了预测，Schmitz［4］等利用统计学方法，基于同步声信号采集，对颤振进行了识别。在国内，宋清华［5］等研究了铣削参数与高速铣削系统动态特性的关系，石莉［6］等基于小波理论，对动态铣削力进行了研究，并预报了铣削颤振，吴玲［7］等，基于遗传算法得到的数据，对铣削加工进行了参数优化。

本文以刀具的模态试验和铣削力仿真试验［8］为基础来构建加工中心的铣削稳定性叶瓣图，通过选取合适的主轴转速和切削深度，避免加工过程中颤振的发生，以保证平面铣削过程的稳定性。

1 铣削颤振的动力学分析

1.1 铣削动力学分析

一个典型的加工中心铣削系统可以简化为一个二自由度振动系统［9］，如图1所示。

图中xoy为刀具坐标系，Ω代表主轴转速，φj是刀齿j的瞬时接触角位移，从切削力法向Y轴往顺时针方向测量其大小，Ω与φj有如下关系：φj（t）=Ω·t。Frj和Ftj是刀齿j的法向和切向的切削力分量。

该二自由度振动系统有X与Y两个互相垂直的自由度。X为切削力的进给方向，Y为切削力的法向，二者共同作用对该系统进行激励并分别引起x和y的动态位移。

图1 二自由度铣削振动模型

铣削过程的动力学方程用微分方程的形式可以表示为［10］：

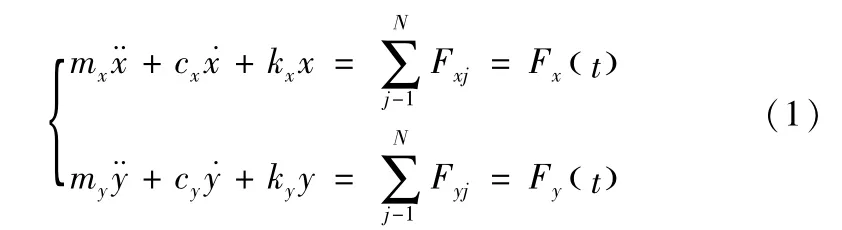
其中，mx、my、cx、cy、kx、ky分别为机床、刀具系统的X、Y两个自由度方向上的质量、阻尼和刚度系数。Fx（t）、Fy（t）分别是切削力在第j个刀齿上的X、Y方向上的两个分量。

铣削加工中，一般只考虑再生颤振的动态切削厚度，其表达式：

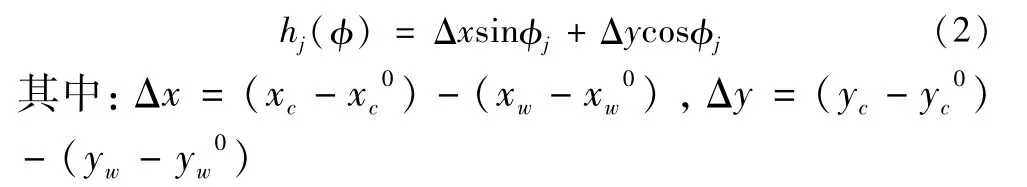
根据Tlusty［11］的正交切削理论模型，切削过程中当瞬时角位移为φ时，动态切削力作用在刀齿j上的切向和径向分量分别为：

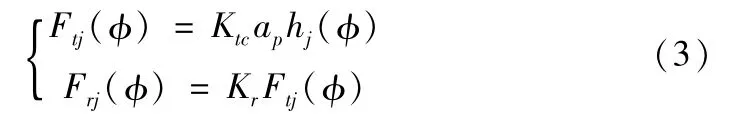
其中Kr=Krc/Ktc为径向力系数与切向力系数之比，Krc为径向力系数，Ktc为切向力系数，ap为切削因素中的切削深度，切向和径向分量的方向如图2所示。

将（2）式带入（3）式，并对X和Y方向上的力求和得：

其中：axx，axy，ayx，ayy为方向系数式。

将（4）式改写为：

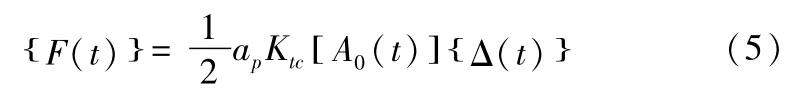
其中：A0（t）为与瞬时角位移φj相关的周期函数，其角频率ω=N·n/60，周期T=2π/ω。对A0（t）进行Fourier级数展开并保留第一项，则（5）式可改写为：

其中：αxx，αxy，αyx，αyy为方向系数式子。

式（6）即为最终推得的动态铣削力公式。

1.2 颤振稳定域算法解析

在刀具-工件之间的接触区识别的传递函数对于整个的颤振稳定域分析过程来说是非常重要的。对（1）式整理，并进行拉氏变换后，将传递函数写成矩阵形式：

其中Gxx（iω）、Gyy（iω）分别为在X方向和Y方向的直线传递函数，Gxy（iω）、Gyx（iω）是两个方向的交叉传递函数。

该系统稳定的充要条件是传递函数G（iω）特征方程的根均具有负的实部。故切削力可表示为：

其中，ωc表示颤振频率。

化简后得：

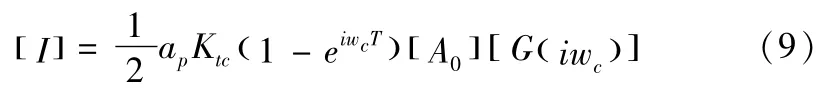
式（9）有非奇异解的条件是特征方程的值为0，即：

进一步得到特征方程的特征值Λ：

则特征方程可以写为：

从而得到特征值的解析值：

由于传递函数为复数，所以特征值包含实数和虚数两部分，令Λ=ΛR+iΛI，e-iwcT=cos wcT-i sin wcT，将其带入（11）式，并令虚部等于0，得到：

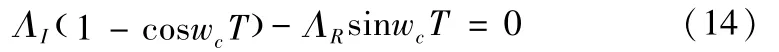
由式（11）和式（14）解析得到临界轴向切削深度和主轴转速：

其中k为叶瓣图中的叶瓣数目，κ=ΛI/ΛR。

由推导出的轴向临界切削深度和主轴转速表达式公式可知：若机床-刀具-工件系统已给定，当知道位于系统固有频率附近的颤振频率ωc、铣刀的齿数N、刀具的切削参数Ktc以及系统的频响函数，便可以求出轴向的临界切削深度以及主轴转速，从而构建出颤振稳定域的叶瓣图［12］。

2 刀具-主轴系统模态实验分析

2.1 模态试验

对于复杂的刀具-工件系统来说，通过仿真得到其模态参数是极其困难且不准确的，故这里采用模态锤击实验的方法，通过对安装在主轴上的刀具进行锤击起振来获得系统的频率响应数据，然后利用相应的仪器直接识别出系统相应的固有频率、刚度和阻尼比等模态参数。

实验对象来自于发动机缸体生产线上工序OP100.2所使用的三轴卧式加工中心，刀具为Kennametal的套式铣刀盘和Kennametal的刀片。其中刀盘的直径D=160mm，可安装刀片数亦即刀齿数Z=18，如下图2所示。

图2 套式铣刀盘和刀片

实验所用设备主要包括北京东方振动与噪声技术研究所的Coinv DASP V10多通道数据采集和信号处理系统；美国国家仪器的NIUSB-9234四通道振动数据采集卡（分辨率24位，动态范围102 dB）；冲击力锤；3个灵敏度为93mv/g的加速度传感器。实验装置示意图如图3所示。

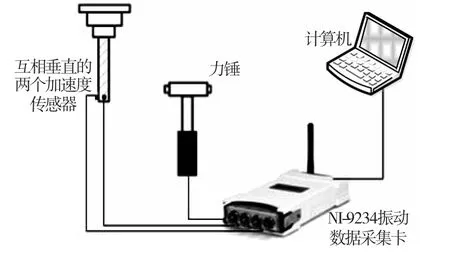
图3 模态试验的装置示意图

试验过程为：在刀尖位置互相垂直的安装两个加速度传感器，在刀盘后面的刀柄上安装一个加速度传感器，用力锤在刀具上远离加速度传感器的一侧进行敲击起振，由数据采集卡将所测得的力信号和加速度信号放大后采集存储到计算机中，然后进行数据分析和处理。铣刀的模态试验现场如4图所示。

实验中设置采样点数为54576个，采样频率为6120Hz。为了降低测试误差，提高测试结果的可信度，共进行3次锤击起振实验，取其中结果较为理想的一组的平均值；每次实验采集X、Y和Z向三个加速度传感器的响应数值：

T1：（X，Y，Z）；

T2：（X，Y，Z）；

T3：（X，Y，Z）。

图4 加工中心刀具-主轴模态试验现场图

实验结束后，在计算机上使用北京东方振动与噪声技术研究所的DASP模态分析软件对采集到的数据进行分析和处理。

2.2 数据处理

由于实际试验中力锤敲击或者采集设备有出现问题的可能，故对以上三次锤击模态试验的结果进行评定，如表1所示。

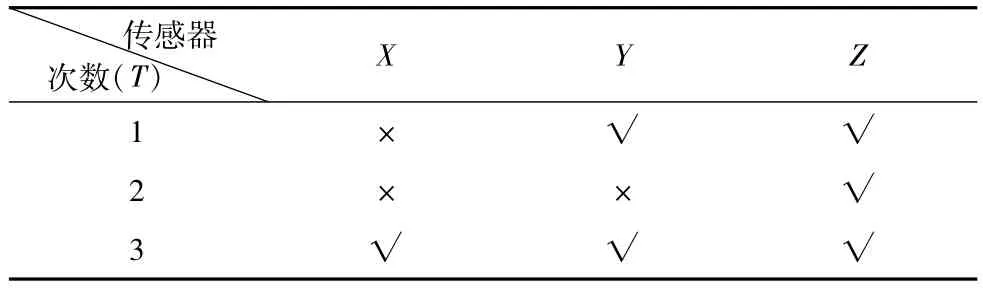
表1 实验数据合格情况表

由表1可知，第3次锤击实验的X、Y和Z三向的响应的实验结果均较为理想，故以此组作为计算刀具模态固有频率、刚度和阻尼比的依据。

第三次锤击模态试验X、Y和Z向加速度传感器相应结果如图5所示。

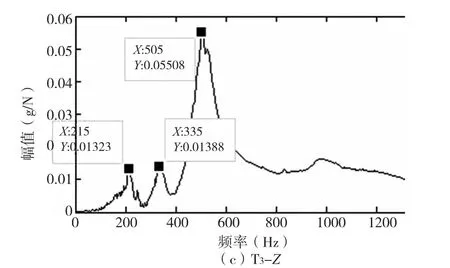
图5 第三次模态试验结果

计算结果如下表2所示。

表2 刀具的参数表

3 铣削仿真实验

本小节利用Deform有限元仿真软件对加工中心进行铣削过程的仿真，得出铣削力系数，为接下来稳定性叶瓣图的构建做准备。

3.1 铣削力系数的辨识理论

Sabberwal［13-14］开铣削力力学模型建立的先河，并在应用和研究中不断改进。其中瞬时刚性力模型在实际应用中预测准确度较高，应用也较为广泛，其基本公式为：

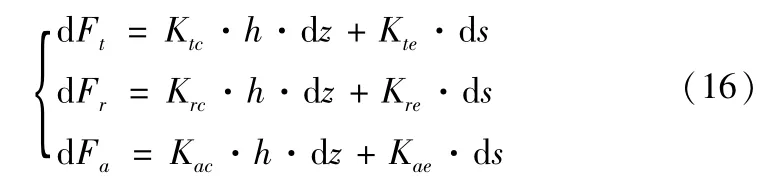
其中d Ft、d Fr、d Fa分别为切削力在切向、径向和轴向的微元，h、d z、d s分别为切削厚度、轴向切深和切削刃的长度微元，Ktc、Krc、Kac、Kte、Kre和Kae分别为切削力和刃口力在切向、径向和轴向三个方向的系数。为了简化计算，令φst=0，φex=π，通过坐标变换和积分运算，可得出在直角坐标系下的每齿周期平均铣削力：

由于刀具-主轴系统在轴向上的刚度较大，这里只考虑XY平面内的切削力Fx、Fy：

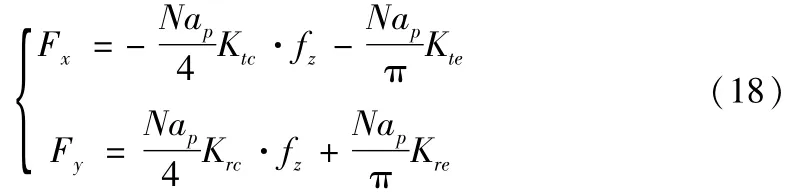
由上式可以看出，N为定值，ap、fz为设置参数常数，Fx、Fy可以通过铣削仿真实验或者实际的铣削力测试实验获得。对于Ktc、Kte、Krc和Kre四个未知数，通过取两次不同切削深度值ap可获得两组切削力Fx、Fy，从而可以解此有四个独立方程组成的四元一次方程组，得到相应的铣削力系数。

3.2 铣削力仿真实验

仿真实验使用Deform工艺仿真系统，仿真分析的主要工作量在于前处理，包括切削参数的定义，刀具和工件的三维建模、网格划分和材料定义等。

（1）切削参数设定

对于车削过程，切削参数即切削用量三要素包括：切削速度（Cutting speed）Vc、进给速度（Feed rate）fv，背吃刀量（Back engagement）即切削深度（Depth of cut）ap。特别地，针对铣削过程来说，ap专指轴向铣削深度，另有径向切削深度ae，表示铣刀在铣削过程中实际参与切削的径向宽度，又称铣削宽度。如图6所示。

图6 铣削参数

本文所研究的该加工中心的铣削加工工艺内容如表3所示。这里所仿真的铣削过程为表3中序号2的内容（半精铣发动机缸体的顶面），如图7所示。刀具为直径d=160mm、刀齿数N=18的面铣刀。

图7 面铣刀加工内容

表3 加工中心加工工艺表

工艺卡片中切削深度ap=0.5mm，在实际的两次仿真实验当中，分别取ap=0.6mm和ap=0.8mm。

主轴转速n=358r/min，每齿进给量fz=0.15mm。故每转进给量：

相应的每分钟进给量，即进给速度：fv=fr·n=2.7×358=966.6mm/min。

最终得到切削速度：

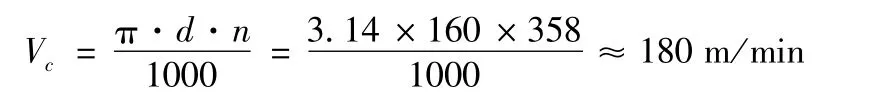
（2）刀具的参数定义和网格划分

刀片材质为KCK15（K-Kennametal，C-涂层硬质合金，K-主工件材料铸铁，15-相对硬度为15）；加工件缸体材质为HT250。

首先利用Pro/E建立刀具单个刀片的三维模型如图8a，并保存为通用的STL格式文件。然后导入到Deform的刀具定义页面中，加载刀具材料参数，选择Tool_Material列表下与实验中所用硬质合金刀具的材料性能参数基本一致的材料。最后进行刀具的网格划分，如图8b所示。

图8 刀具三维模型的建立和网格划分

（3）加工工件的定义和网格划分

根据加工件材料和经验，选择Steel目录下的AISI-1020（Machining）为工件材料。

设定工件的各项参数，生成工件几何模型。工件的网格划分结果为单元数目50976个，节点数目11989个，如图9所示。

图9 工件的网格划分

（4）模拟条件的设定和分析

设定内容主要是数据的存储步数、终止条件和磨损条件等，完成仿真的前处理，然后生成数据文件，并以此为基础进行有限元铣削仿真分析计算（如图10），计算完毕打开后处理程序查看模拟结果。

图10 铣削仿真

3.3 数据处理

铣削仿真实验完成后，进入后处理页面查看分析结果。在ap=0.6mm和ap=0.8mm两次铣削过程仿真实验下，得到两组平面内的铣削力Fx、Fy，根据式9的结论，将所有已知数带入获得除Z向外的4个铣削力系数，结果如表4所示。

表4 铣削力系数

4 颤振稳定域页瓣图的构建

根据刀具-主轴模态试验得出的刀具固有频率和切削力仿真实验的得出的铣削力系数，利用1.2小节得出的结论，使用Matlab软件进行叶瓣图构建的相关编程编写，最终绘制出该面铣刀进行缸体顶面铣削加工时的稳定性叶瓣图，如图11所示。

图11 铣削颤振稳定域分析叶瓣图

从叶瓣图可以看出，当切削参数（主轴转速和切削深度）在曲线下方时，铣削处于稳定加工区域；若选择在曲线下方的横虚线下面的区域，则为绝对稳定加工区域；相反将切削参数选在位于曲线上方的区域，则非常容易发生颤振。

从图11也可以看出：转速在超过200rev/min后，切削深度与主轴转速成正相关而不再形成叶瓣图，经分析可能是由于直径160mm的铣刀刚度较大造成。而实际生产中主轴转速为358rev/min，从叶瓣图可以看出此时临界切削深度约为0.9mm。

5 结论

基于某柴油发动机缸体生产线工序OP100.2所用卧式加工中心的加工内容，研究了该机床铣削加工过程中的颤振稳定性问题。构建了铣［参考文献］

削加工时的稳定性叶瓣图，以指导切削参数（主轴转速和切削深度）的选择和改进，避免铣削加工中颤振的发生，从而获得加工精度比较高的表面质量。该方法简单方便，可靠性高，具有较大的实际应用价值。

［1］Faassen R.Chatter Prediction and Control for High-Speed Milling［D］.Eindhoven：Eindhoven University of Technology，2007.

［2］Gagnol V，Bouzgarrou BC，et al.Model-based chatter stability prediction for high-speed spindles［J］.International Journal of Machine Tools&Manufacture，2007，47（7-8）：1176-1186.

［3］Kivanc E，Budak E.Structural modeling of end mills for form error and stability analysis［J］.International Journal of Machine Tools and Manufacture，2004，44（11）：1151-1161.

［4］Schmitz T L.Chatter recognition by a statistical evaluation of the synchronously sampled audio signal［J］.Journal of Sound and Vibration，2003，262（3）：721-730.

［5］宋清华，唐委校.高速铣削系统动态实验方法研究［J］.组合机床与自动化加工技术，2005（9）：21-23.

［6］石莉，贾春德，孙玉龙.应用小波研究动态铣削力及预报铣削颤振［J］.哈尔滨工业大学学报，2006，38（10）：1978-1980.

［7］吴玲，左健民，王保升，等.基于遗传算法的铣削参数优化［J］.组合机床与自动化加工技术，2014（4）：108-111.

［8］郝洪艳，汤文成，王保升.基于铣削力与稳定性预测的铣削工艺参数优化［J］.组合机床与自动化加工技术，2013（10）：43-46，49.

［9］Budak E，Altintas Y，Armarego E JA.Prediction ofmilling force coefficients from orthogonal cutting data［J］.Transactions of the ASME Journal of Manufacturing Science and Engineering，1996，118（2）：216-224.

［10］丁烨.铣削动力学-稳定性分析方法与应用［D］.上海：上海交通大学，2011.

［11］Tlusty J，Ismail F.Basic Non-linearity in Machining Chatter［J］.CIRP Ann-Manufacture Technology，1981，30：299-304.

［12］Altintas Y，Ko J H.Chatter Stability of Plunge Milling［J］.CIRP Annals，2006，55（1）：545-556.

［13］Sabberwal A J.Chip section and cutting force during the milling operation［C］.Annals of the CIRP，1961，10（3）：197-203.

［14］Koenigsberger F，Sabberwal A JP.An Investigation into the Cutting Force Pulsations During Milling Operations［J］.International Journal of Machine Tool Design and Research，1961，1：15-33.

Research on M illing Stability of M achining Center MDH80

LIYong-yao1，2，CONG Ming1，2，LUO Meng-ran1，2，LIHong-kun1，2，DU Li-qing3
（1.Dalian Xinyu Science Technology Development Center CO.，LTD，Dalian Liaoning 116024，China；2. School of Mechanical Engineering，Dalian University of Technology，Dalian Liaoning 116023，China）

High quality on the joint face between the engine cylinder block and head is required.Chatter stability problems of milling process are analyzed.Hammer modal test and milling force simulation experiments are conducted to get the low modes’parameters and the milling force coefficient of the tool.Cutter chatter stability lobe diagram is built to guide the selection and improvement of cutting parameters.We can select the appropriate spindle speed and depth of cutting through this method，avoiding the occurrence of chatter behavior.It can keep the required accuracy of the workpiece.At the same time，it can protect the tool and machine to improve their service life.

machining center；milling stability；cutting chatter

TH166；TG502.14

A

1001-2265（2015）04-0037-05 DOI：10.13462/j.cnki.mmtamt.2015.04.009

2014-08-18；

2014-10-17

国家＂高档数控机床与基础制造装备＂科技重大专项课题（2013ZX04012071）

李泳耀（1991—），男，河南商丘人，大连理工大学硕士研究生，研究方向为机床精度稳定性分析，（E-mail）liyongyao1991@163.com。