函数带误差的部分线性模型约束下的统计推断
2015-11-02李梦含夏小超
李梦含,夏小超
(重庆大学数学与统计学院,重庆401331)
0 引言
近年来,半参技术发展迅速并广泛应用到经济、金融、政治、生态等科技领域.一方面,参数模型常因设定错误引起较大偏差,而半参技术可以减少设定错误的风险从而避免所谓的“维数灾难”;另一方面,半参技术还拥有非参模型的灵活性.而在半参模型中,部分线性模型发展尤为迅速,为研究温度和用电量的关系,Engle等率先提出了以下形式的这种模型[1]

这里T代表向量或矩阵的转置,Y∈R1为响应变量,X∈Rp和T∈R1是协变量,g(·)是定义在[0,1]上的未知函数,β=(β1,…,βp)T是未知参数变量.在协变量给定时,误差项ε独立且条件均值为零.但在实际应用中,可能由于测量工具或环境因素的影响,使得协变量的测量存在误差,例如血清胆固醇水平、尿钠氯化物水平和接触污染物程度往往受测量误差影响[2].
当协变量的测量存在误差时,模型(1)被称为协变量误差模型或EV模型.一般有3种EV模型:
(i)只有X存在测量误差,即W=X+ξ;
(ii)只有T存在测量误差,即U=T+η;
(iii)X和T都存在测量误差,即W=X+ξ,U=T+η.
致力于研究EV模型参数估计和统计推断的文献也很多.为处理情形(i),Liang等利用常用的衰减参数校正(parametric correction for attenuation)研究参数估计和非参估计的性质,并证明了估计值的渐近正态性和一致性[3];Cui和Li利用最近邻广义二乘法(nearest neighbor-generalized least square method)得到了参数估计值、模型误差的方差和平滑函数[4],Cui考虑了反复测量观察值时的参数估计问题[5];赵和周利用最小二乘和拉格朗日乘子检验进行了统计推断[6];You等检验了统计推断的3个方面:带宽选择技术、拟合优度的检验、基于非凹惩罚似然法的变量选择[7];这些文献都是针对点估计进行的,当然也有很多基于经验似然构造参数置信区间的文献[8-10].总的来说,非参误差问题比参数误差更难处理,更涉及了非参回归模型中的反卷积技术.为研究参数估计的性质,Liang首先将该方法推广到函数带误差的部分线性模型中[11].为了处理情形(ii),Huang则采用经验似然法构造了参数的置信区间[12];此外Zhu和Cui也构造了参数估计值和非参核估计[13].
此处重点研究参数包含辅助信息的情形(ii).在统计应用中,样本外得到的辅助信息可提高参数估计的有效性,正如Rao等在线性模型中所述,当参数的先验信息表示成线性约束时,约束最小二乘估计比普通最小二乘更有效[14].而当线性部分的协变量存在测量误差时,Wei对变系数部分线性模型做了统计推断[15].
受Wei的启发,对情形(ii)在如下约束条件下作统计推断:

A是k×p的已知矩阵,b是k×1的已知常数向量,并假定rank(A)=k<p.
第2节提出参数分量的约束估计和其主要性质;第3节对约束条件的合理性进行检验;第4节是数值模拟;主要结论的假设和证明则在第5节给出.
1 约束估计值的构造及其性质
为完成各种证明,需假设一些条件成立.
令 xij为 Xi的第 j个分量,hj(t)=E(xij|Ti=t),ζij=xij-hj(Ti),ζi=(ζi1,…,ζip)T,1≤i≤n,1≤j≤p.首先提出平滑和超平滑的定义.
定义1[16]u的误差分布被称为α阶平滑的,如果它的特征函数φu(·)满足t→∞时,

其中 d0,d1,α 均为正数.
定义2[16]u的误差分布被称为α阶超平滑的,如果它的特征函数φu(·)满足t→∞时,
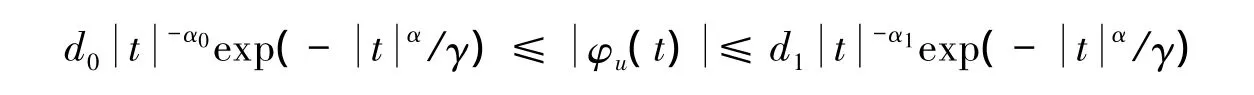
这里 d0,d1同,α,γ 均为正数,α0和 α1为常数.
然后指出如下假设条件:
(C1)g(·)和hj(·)(1≤j≤p)一阶Lipschitz连续;
(C2)不可观测协变量T的边缘密度在区间[0,1]上从零到无穷有界,且有有界的m阶导数,m是正整数;误差u的分布是平滑或超平滑的,且其特征函数φu(·)不为0;
(C3)核函数K(·)对称,且为 m阶对称,即满足 K(-t)=K(t)(t)d t≠0,t)d t=0,其中 j=1,2,…,m-1.
(C4)误差分布满足下列两个条件之一:
(i)误差分布是 α 阶平滑的,取平滑参数 h=dn-1/(2m+2α+1),其中 d>0,2m>2α+1,并假定对于常数 c≠0,当t→∞ 时(t)=O(1),且有


这里,测量误差 ui均值为零,独立同分布,且独立于(Ti,Xi,εi),β∈Θ⊆Rp,(X,T)给定时 εi的条件均值为零,并假定εi同方差.另外为使模型(3)可识别,进一步要求u有已知分布的特征函数φu(·).
记T和U的密度函数分别为fT(·),fU(·),定义fT(t)的反卷积核估计为[16]

下面的定理将说明式(7)和式(8)的一致性.
定理1 假设条件(C1)-(C6)成立,有
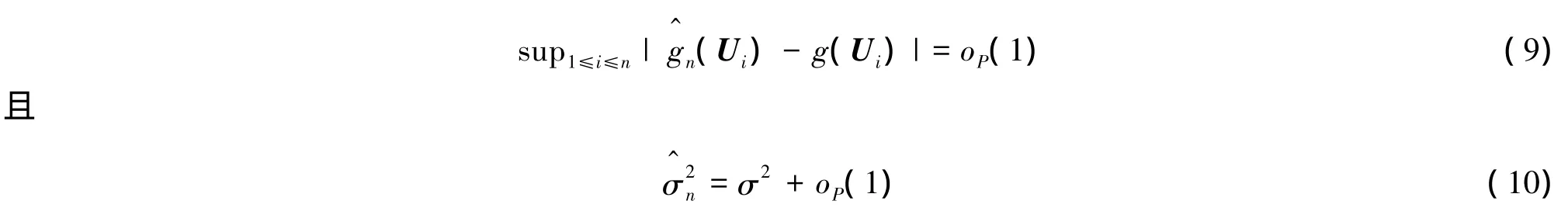
下面将用两种方法构造参数的约束估计.
1.1 拉格朗日乘数法
Liang证明了PLS估计值的一致性和渐进正态性[11],但并没有考虑约束条件的存在,而有效的约束可以减少估计偏差.本节考虑约束条件(2)并在第3节对约束条件的合理性进行检验.首先,应用拉格朗日乘数法构造惩罚函数
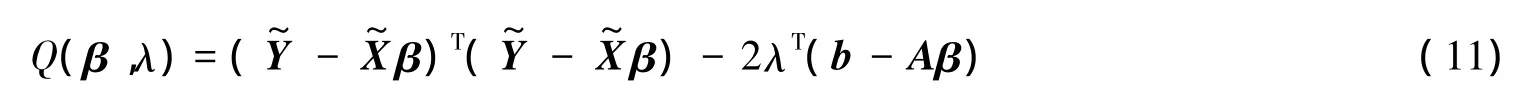
最小化式(11)得到参数估计值.通过求解最优化问题,即把Q(β,λ)分别对β和λ求偏导令其为零,得到

由式(5),定义g(t)的非参约束估计为
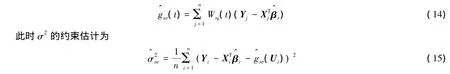
定理2(i)假设(C1)-(C5)成立,则有

推论1 在定理2的条件下,若β接近参数的真值,则有
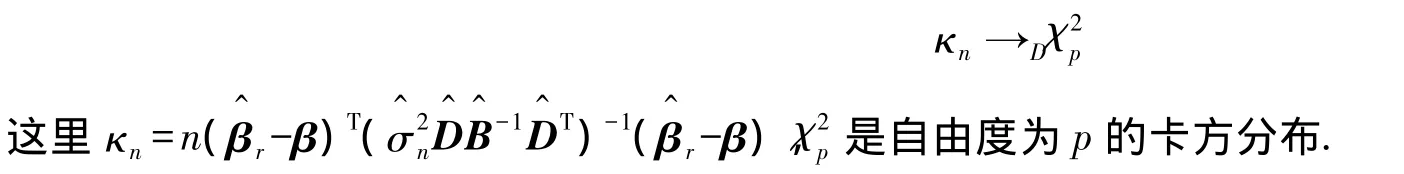
接下来介绍另一种构造β约束估计值的方法.
1.2 方法 2
将Wei在部分线性EV模型中得到的参数约束估计方法应用到本文的模型中[15],过程如下.
定义 p×(p-k)矩阵 R 使得 QT=^(AT,R)满秩且 AR=0,此时 R 存在但不唯一[17].记 Q-1=[AT(AAT)-1,R(RTR)-1],再令 θ=Qβ,则有 θ=(,其中 θ1=Aβ,θ2=RTβ.
令 G=(g(T1),…,g(Tn))T,ε=(ε1,…,εn)T,知模型(1)的矢量形式为 Y=Xβ+G+ε.再由 Aβ=b,则模型可改写为

这里X*和Y*如式(6)中所定义,但权重Wnj(·)的Kn(·)却是一般核函数的重新排列.当替代变量U可观测时,类似于式(6)有θ2的估计值

2 参数的约束条件检验
考虑模型(3)线性部分参数带有约束条件的情形,对约束条件的合理性进行检验.不失一般性的考虑如下带有线性假设的检验:

Fan和Huang提出部分变系数模型参数的profile广义极大似然比检验[18],并证明了Wilks现象的存在,即原假设成立时该统计量近似服从与σ2无关的卡方分布.应用该方法检验模型(3)的式(22),发现Wilks现象仍然存在,但当线性部分存在测量误差时却不存在Wilks现象[15].本节检验过程如下:
原假设成立,即Aβ=b时,参数的约束估计βr和非参估计gnr(t)分别由式(13)和式(14)给出.相应的残差平方和为

如果H0为真,直观上RSS0和RSS1不应相差过大.所以当GLR统计量较大时,应拒绝原假设.理论说明由定理4给出.
定理4 若检验式(22)的原假设和(C1)-(C6)成立,则有,,这里是自由度为k的卡方分布.
定理5 若检验式(22)的备则假设和(C1)-(C6)成立,则有(δ),这里(δ)代表自由度为k,非中心化的卡方随机变量,其中非中心参数为

注:定理4说明原假设成立时,Tn与σ2,β和g(·)无关,近似服从自由度为k的卡方分布.这个定理既提供函数带误差的部分线性模型参数分量检验的方法,也说明了Wilks现象依然存在.虽然只考虑了约束参数分量的检验,但也可用类似的方法进行非参函数的检验.
3 数值模拟
为对约束估计值和统计量Tn进行检验,本节在有限样本下作数值模拟,数据由下产生

这里(xi1,xi2)由相关系数为 0.4 的二维标准正态分布产生,Ti~N(0.5,0.252),g(t)=.为研究误差分布对参数估计值的影响,检验如下两种情形:ui由双指数分布(平滑情况)产生;ui由正态分布(超平滑情况)产生.假设为误差ui的方差,并取),则该信噪比可达 0.7[16].
例1 双指数误差
假设误差u有如下双指数密度函数

核函数K(·)是高斯核,即标准正态密度.简单计算可知式(4)中的核Kn(·)可由如下定义
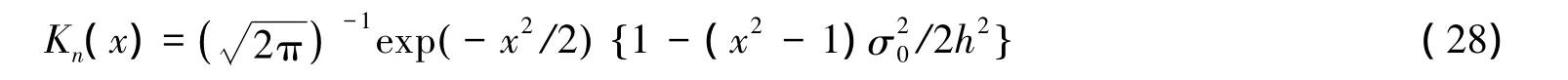
根据条件(C4)(i)选取 h=1.16·sd(T)·n-1/9[19].
例2 正态误差

根据(C4)(ii)选取 h=1.1σ0(log n)-1/2.
3.1 约束估计的一致性检验
在模型(26)中,令β1=1,β2=3.考虑约束3β1+β2=6和模型误差ε分别是均匀分布、正态分布、学生t-分布、卡方分布的情形,分别给出约束估计的样本均方误差(MSE)和样本标准差(SD),其中

表1 和的均方误差和标准差

表1 和的均方误差和标准差
?

续表1
由表1知,当样本量增加时,均方误差和标准差在递减.说明随着样本量增多,约束估计逐渐接近真实的参数,与结论一致.
3.2 检验统计量有效性检验
对模型式(26),考虑如下检验:

关于β1=2,β2=2-c,c=0表示原假设,否则就是备则假设.
原假设成立时,对样本量为n=100的情形运行1 000次来检验统计量Tn是否服从定理4的(k=1).图1,2分别描绘了均匀误差下例1,例2的误差Q-Q图,也揭示了1 000个GLR统计量的四分位数和分布四分位数的关系,可以看出GLR统计量可以很好的拟合期望的卡方分布,也与之前结果一致.
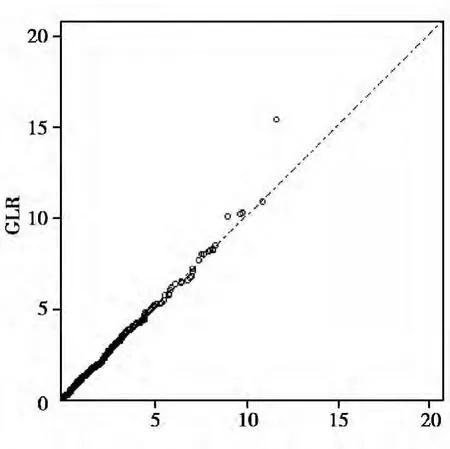
图1 例1的Q-Q图

图2 例2的Q-Q图
为评估第3节提出检验过程的有效性,重复1 000次得到检验统计量的功效曲线.图3描绘了GLR检验的功效曲线,拒绝率是根据显著水平α=0.05在不同的样本量下计算的,从图3可以看出当样本量增大时检验效果变好,这也说明了检验过程是有效性.图4描绘了固定样本量n=100时施加不同模型误差的情形,如图所示,模型误差时正态分布、卡方分布、学生t-分布的情形相似,但当c离0较近时,均匀分布下的情形有所不同.例2的结论类似可得(图5,6).
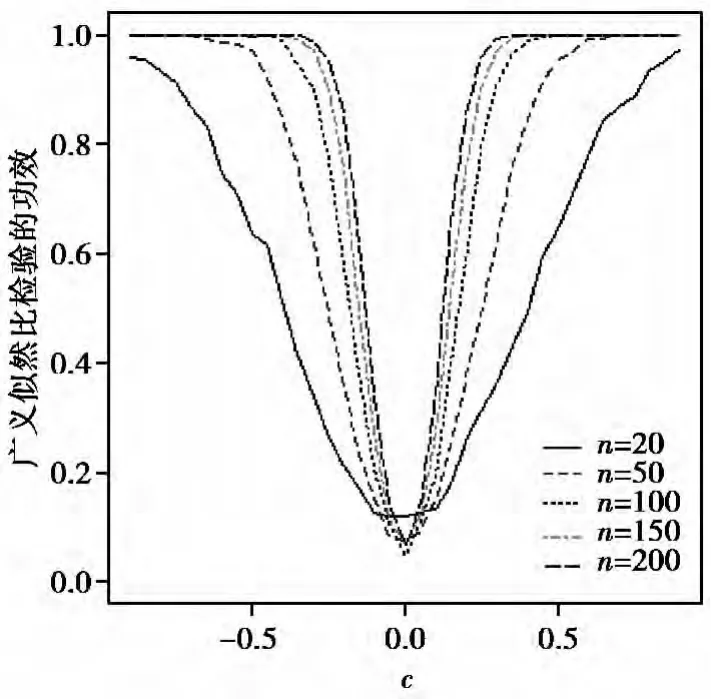
图3 不同样本量下例1的功效曲线

图4 不同模型误差下例1的功效曲线

图5 不同样本量下例2的功效曲线

图6 不同模型误差下例2的功效曲线
4 主要结论的假设和证明
最后在证明结论前,先介绍如下引理.

(ii)如果 U是超平滑误差,X和 T独立,(i)的结论对于 j=1,…,p仍然成立,但是
定理1的证明 首先证明式(9).由

再由式(9)就得到了(ii)的第一个结论.
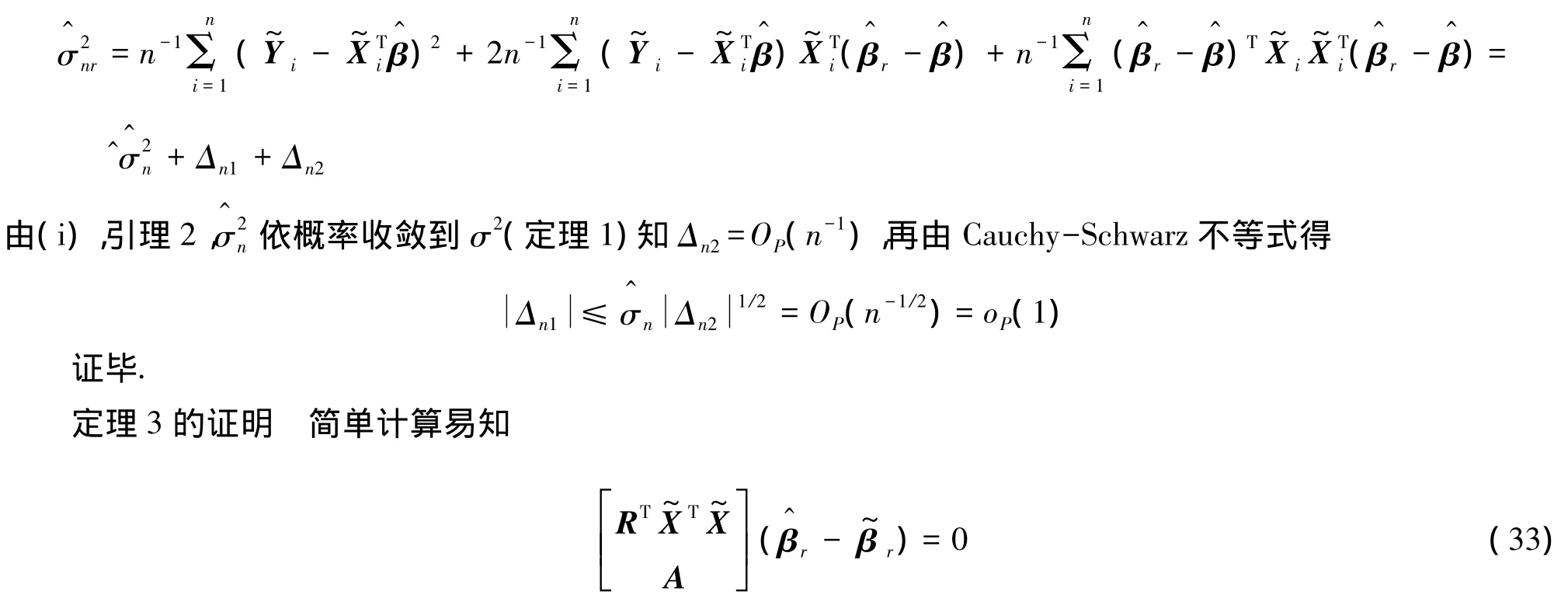
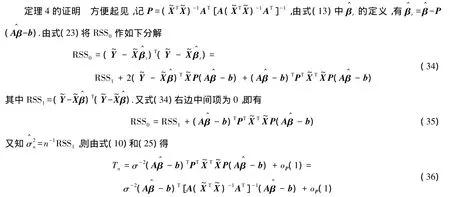
由引理2和引理3知

所以,在原假设成立即 H0∶Aβ-b=0时,可得.证毕.
定理5的证明 证明方法和定理4的证明相同,此处省略.
[1]ENGLE R,GRANGER C,RICE J,et al.Nonparametric Estimates of the Relation Between Weather and Electricity Sales[J].Journal of American Statistical Association,1986(81):310-320
[2]YOU J H,ZHOU Y,CHEN G M.Corrected Local Polynomial Estimation in Varying-coefficient Models with Measurement Errors[J].The Canadian Journal of Statistics,2006(34):391-410
[3]LIAN H,HÄRDLEW,CARROLL R J.Estimation in a Semiparametric Partially Linear Errors-in-variables Model[J].The Annals of Statistics,1999(27):1519-1535
[4]CUI H J,LI R C.On Parameter Estimation for Semi-linear Errors-in-variable Models[J].Journal of Multivariable Analysis,1998(64):1-24
[5]CUI H J.Estimation in Partial Linear EV Models with Replicated Observations[J].Science China Mathematics,Series A.2004(34):467-482
[6]赵培信,周小双.线性误差协变量下部分线性模型的约束统计推断[J].山东大学学报:理学版,2014,49(7):69-74
[7]YOU J H,XU Q F,ZHOU B.Statistical Inference for Partially Linear Regression Models with Measurement Errors[J].Chinese Annals of Mathematics,Series B,2008(29):207-222
[8]LI G R,XUE L G.Empirical Likelihood Confidence Region for the Parameter in Partially Linear Errors-in-variables Model[J].Communications in Statistics-Theory and Methods,2008(37):1552-1564
[9]WONG H,LIU F,CHEN M,et al.Empirical Likelihood Based Diagnostics for Heteroscedasticity in Partially Linear Errors-invariables Models[J].Journal of Statistical Planning and Inference,2009(139):916-929
[10]LIU Q,XUE L G.Empirical Likelihood Confidence Regions of Parameters in Nonlinear EV Models under Missing Data[J].Acta Mathematica Scientia,Chinese Series A,2012(32):233-245
[11]LIANGH.Asymptotic Normality of Parametric Part in Partially Linear Models with Measurement Errors in the Nonparametric Part[J].Journal of Statistical Planning and Inference,2000(86):51-62
[12]HUANG Z S.Empirical Likelihood for the Parametric Part in Partially Linear Errors-in-function Models[J].Statistics and Probability Letters,2012(82):63-66
[13]ZHU L X,CUI H J.A Semi-parametric Regression Model with Errors in Variables[J].Board of the Foundation of the Scandinavian Journal of Statistics,2003(30):429-442
[14]RAO CR,TOUTENBURG H,SHALABH,et al.Linear Models and Generalizations:Least Squares and Alternatives[M].Berlin:Springer,2008
[15]WEI C H.Statistical Inference for Restricted Partially Linear Varying Coeficient Errors-in-variables Models[J].Journal of Statistical Planning and Inference,2012(142):2464-2472
[16]FAN J Q,TRUONG Y.Nonparametric Regression with Errors in Variables[J].The Annals of Statistics,1993(21):1900-1925
[17]AMEMIYA T.Advanced Econometrics[M].Boston:Harvard University Press,1985
[18]FAN J Q,HUANG T.Profile Likelihood Inferences on Semiparametric Varying-coefficient Partially Linear Models[J].Bernoulli,2005(11):1031-1057
[19]CHEN X,CUI H J.Empirical Likelihood Inference for Parameters in a Partially Linear Errors-in-variables Model[J].Statistics,2011(46):745-757
