模型“出面”、繁简转换*

☉湖南省常德市芷兰实验学校初中部　陈金红

☉湖南省常德市安乡县芦林铺中学　郭作华

模型“出面”、繁简转换*

☉湖南省常德市芷兰实验学校初中部陈金红

☉湖南省常德市安乡县芦林铺中学郭作华

解压轴题一般有很多种方法，但多数人包括命题者给出的常常是思路不明、计算或推理复杂的做法，指导效果当然就不佳！但若重视提炼问题的本质模型、解析出方法的细节生成，即可有效提高压轴题的教学与应试效果.众所周知，利用模型思想解数学问题的确能使复杂问题简单化，优化解题过程，提高解题速度，因此，模型“出面”、繁简转换，现运用此观点解析一例：2013年成都中考数学压轴题.

（1）如图1，若该抛物线过A，B两点，求该抛物线的函数表达式.

（2）平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q.

①若点M在直线AC下方，且为平移前（1）中的抛物线上的点，当以M、P、Q三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点的坐标；

图1

对于（2）的第①问，先看命题者的思路，求出直线AC的解析式、平移后的抛物线方程，解它们构成的方程组，求出点P、点Q的坐标，最后对线段PQ分类：PQ为直角边、PQ为斜边两种情形，艰辛“努力”才做出来的，有点“咬牙切齿”的味道！

真的有这么难吗？促使我们有换个角度看问题的冲动：因为直线AC是固定不动的，要得到一个其上线段PQ为边的等腰直角三角形，易使人联想到等腰直角三角形的背景即正方形模型（本题模型之一），再把点M代入原抛物线解析式，有解即存在、找出了符合要求的M点！简洁明快！

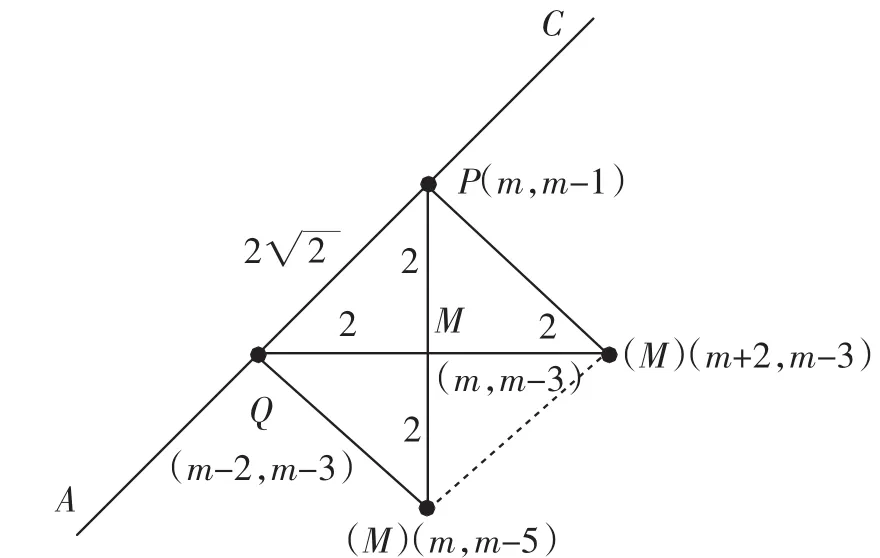
图2

具体即不难知直线AC的解析式为y＝x-1．与x轴正方向夹的锐角为45°，设平移前的抛物线的顶点为P0，则由（1）可得P0的坐标为（2，1），发现顶点P0在直线AC上．又点P在直线AC上滑动，故可设P的坐标为（m，m-1），则平移后的抛物线的函数表达式为

当PQ为斜边时，即图2中左上角的等腰Rt△PQM，不难知PM∥y轴、QM∥x轴，于是点M的坐标为（m，m-3），再把点M代入到原抛物线+2x-1中得m-3=，于是有，解得m=

当PQ为直角边时，即图2中左边的大等腰Rt△PQM（或上边的大等腰Rt△PQM），同上，不难知点M的坐标为（m，m-5）或点M的坐标为（m+2，m-3），再把点M代入到原抛物线中，可得到M3（4，-1），M4（-2，-7）.

综上所述，所有符合条件的点M的坐标为：M1（1+M4（-2，-7）.

对于（2）的第②问，命题者的解法没有给人“所以然”的交代，计算量大，让人理解起来冲淡了主题、有些晦涩之感！

真的有这么难吗？同样促使我们通俗化解读之的动机：尽管P、Q是动点，但始终有PQ=是个定值不变量（求式的分子解决了）！转而关注求式的分母NP+BQ取最小值时，必有有最大值；要NP+BQ取最小值最直接的联想是“将军饮马”对称应用模型，但如何使用？是本问题的最大“障碍”点！

此时由PQ∥FN、PQ=FN，知四边形PQFN为平行四边形，于是求式分母中的PN项可由FQ替代了，即NP+ BQ=FQ+BQ，其中点B、点F是定点，转化为研究定直线AC上动点Q的位置（它直接决定了动点P的位置！）于是有：

“将军饮马”模型（本题模型之二）：即“已知定点B、F和定直线AC，在直线AC上找一点Q，使得FQ+BQ（=NP+ BQ）取得最小值”（求式的分母解决了）！

图3

图4

具体即取点B关于AC的对称点B′，连接QF，QB′，如图3，当B′、Q、F三点共线时，FQ+B′Q（=NP+BQ）最小，最小值为线段B′F的长度！在Rt△B′FE中去求！

综上可知，关注分子，关注分母，数值联想，模型凸显，方法实施，整体到局部，和谐流淌，如沐思维、思想之春风，如乘模型之载体，如启方法之动力，彰显灵气之融融！要害之处仍是“模型出面”，发现“繁简转换”，方法、过程呼之既出！对比原解法、期刊对其研究已发之文，很快可知运用上面的方法更简单、更通俗、更本质化！这也是我们毕业班老师和命题者自身要注意的问题.

1.陈金红.习题磨练结构谋法［J］.中学数学（下），2011（4）.

2.陈金红.让解法来得更自然一些［J］.中学教研（数学），2014（12）.

3.陈金红.几何“形”，代数“声”，三角函数“心”——谈2014年湖南省常德市中考压轴题［J］.中国数学教育（初中），2014（10）.

4.陈金红.不要放弃更初等的想法［J］.中学数学教学参考（上），2012（1～2）.

*本文系全国教育科学“十二五”规划2013年度教育部规划课题《生命课堂视野下的教学案例研究》（课题编号：FHB130512）的阶段性成果之一.