TB2零件表面加工应力的测量及其有限元变形预测*

王 毅

（丽水学院工学院，浙江丽水 323000）

TB2零件表面加工应力的测量及其有限元变形预测*

王 毅

（丽水学院工学院，浙江丽水 323000）

在对TB2零件车削加工后，被加工面会有一层加工引起的内应力层，通过对加工进行逐层腐蚀剥层，并用应变片测量此过程中零件内壁应变的变化，最终得到了其加工表面随深度变化的内应力值。为计算此表面内应力对于零件变形的影响，将测得的随深度变化的内应力施加给有限元模型进行计算。由于零件是圆柱形，因此模型中的不同的网格单元所施加内应力均不一样，编程的方法，根据节点的坐标计算网格单元的应力，最终算得的应力文件中包括每个网格单元的所要施加的不同的应力值，将计算结果通过文件导入的方法施加给有限元软件，通过有限元的计算，最终得到了零件因表面内应力而引起的变形。

应变；内应力；化铣；有限元分析

0 引言

金属切削加工是一个伴随着高温、高压、高应变率的塑性大变形过程，以及热应力和相变等因素的综合作用［1-2］，在已加工的表面层上会产生加工内应力，其在工件表面上的分布较浅（一般不超过0.2mm），但在深度方向有着较高的变化率，其值的精确测量有一定的困难。

工件机械加工引起的表面内应力的分布会严重影响已加工零件的静力强度、疲劳强度及抗腐蚀性能［3］，同时还会严重影响零件几何尺寸稳定性［4，6］，从而严重影响了零件的使用性能，制约零件的服役寿命。如此看来如何测量并控制机械加工过程引入的表面内应力显得至为重要。

在一些对零件尺寸精度要求高的领域，如航空航天领域，诸如TB2类的钛合金的使用越来越广，其在加工过程中所引入的内应力对零件产生的变形的影响往往是一个不得不考虑的因素，因此如何准确测量随身的变化的表面内应力并用测得的应力预测零件的变形显得尤为重要。

内应力的测试技术开始于上世纪30年代，发展至今形成了多种测量方法，主要分为有损检测和无损检测两大类。有损检测方法主要有钻孔法、盲孔法、取条法、切槽法、剥层法等，目前应用主流是钻孔法。无损检测方法主要有X射线衍射法、中子衍射法、同步衍射法、超声波法、电子散斑干涉法和磁性法等，其中X射线衍射法是主流方法［6-10］。传统的用X射线法结合腐蚀剥层测量表面随深度变化的加工内应力的方法，其修正方法过于复杂，而且对零件和应力都有较高的要求，另外X射线应力仪价格昂贵，且其测量结果也会存在不可忽略的误差，因此这里介绍一种通过内壁应变的变化计算外壁随深度变化的内应力的方法，其计算可靠，且免去了以往较为复杂的修正过程。

1 加工过程

对TB2零件的外表面进行车削加工，由于钛合金TB2材料属于难加工材料，因此为保护刀具，所采用的切削参数为；切削速度v=30m/min，进给量f=0.02/rev，切削深度dp=0.5mm，加工过程采用冷却液，加工好后用线切割截取一段，最终零件内经为d= 43mm，外径D=45mm，轴向长度L=50mm，如图1所示。

图1 加工后的零件

2 通过测得的应变计算内应力

对于车削加工表面内应力的测量，目前最常用的方法是X射线法结合腐蚀剥层的方法对加工引起的随深度变化的内应力进行逐层测量。每去除一应力层后零件内的原先的内应力的平衡状态会遭到破坏，进而剩余部分的内应力会重新分布而形成一个新的平衡状态，因此新表面的内应力也会发生一定的变化，使得X射线法测得应力值与原先实际的应力值有一定的偏差，必须对X射线测得的应力进行修正补偿才能得到原先正确的应力分布。目前大部分测量者并不对剥层后侧的的应力值得进行修正，这往往会引起一定的误差。在应力修正方面，目前最使用最多的还是1958年Moore and Evans提出M&E修正法，目前在该方面并有太大的进展［11-12］，目前该修正方法仍然是工业上运用比较广泛的修正方法。其修正公式如下；

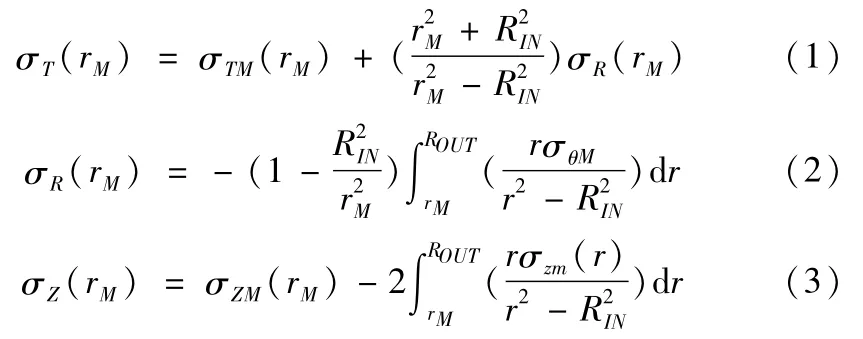
其中，σT，σR，σZ分别为修正后的切向、径向以及轴向应力值，σZM和σTM分别为实际X射线法测得的轴向很切向的应力，ROUT、RIN以及r分别为零件的外半径、内半经以及实际测量处的半径值。

以上修正公式的缺点很明显，其计算太过于复杂，而且其对零件的形状以及应力都有很严格苛刻的要求，因此，在很多场合其往往并不是很受青睐［12］。

这里介绍一种通过测量应变变化并对结果自行修正的计算内应力的方法。

2.1 根据应变计算内应力原理

设定圆筒的内半经为a，外半径为b，σz、σт、σr分别为零件轴向、切向和径向的应力。现在分析从外径b到半径ρ的内层被去除所得到的结果。

设从半经b到半径为ρ的应力层内其内应力的平均值为σ（ρ），当其被释放后，与该层被剥层去除后在半径为ρ的外表面上加上大小相等符号相反的σ（ρ）是等效的［13］。在此设定σza、σta、σra分别为去除外层后在圆筒外表面上所产生的额外的轴向，切向以及径向这三个方向的应力。在初始状态下其内应力是自相平衡的。将所去除的外层看作一个完整的整体，由于在去除前其外壁径向并未有任何力的作用，因此σra为零，根据Lame圆筒理论可以得到；

令εza、εta、εra分别为圆筒内表面上轴向、切向以及径向的应变，应力与应变的关系如式（5）、（6）、（7）；

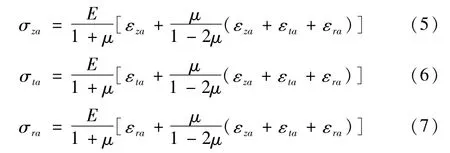
式中E、μ分别表示杨氏模量和泊松比，由σra为零可以得到；

由式（6）、（8）消去εra并从式（4）中可以得到径向内应力为；

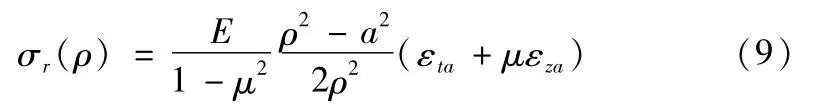
同时横截面上的内应力必须满足轴对称平面问题的平衡；

在无任何外力作用下，内应力的分布应当满足轴向与切向的平衡；

将式（9）代入式（10）可以得到切向内应力的表达式为；

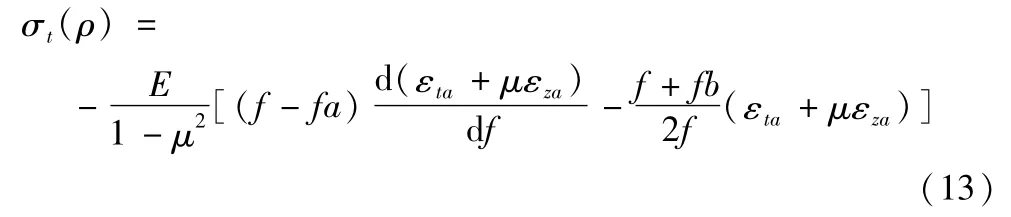
其中fa=πa2，f=πρ2。将圆筒内壁从半径b至半径ρ部分的材料去除后，剩余部分所产生的额外应力可以认为是均匀分布在圆筒截面上的，根据此假设以及式（11）的平衡条件可得；

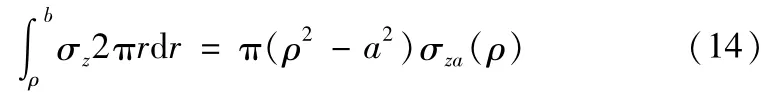
将式（11）对ρ进行求导，可以得到；

将式（8）代入式（5）消去εra，并代入式（15），可以得到轴向内应力为；

综上所述，其外壁加工引起的内应力可以用以下公式进行计算得到；

2.2 应力计算结果

根据以上公式，可以通过测量管外表面轴向和切向的应变的变化，获取管内壁切向和轴向的内应力。采用半桥连接法，由于在测量过程中室温会发生一定的变化，因此必须采用补偿片对温度的变化进行补偿，如图2所示。

图2 应变测量装置

其中补偿片的应变值的变化完全由温度的变化而引起，在测量过程中补偿片不受任何外力的作用，通过应变仪和电脑记录每次腐蚀去除材料层后外壁应变的变化。根据测得的应变以及前面推导的公式最终计算得到的表面随深度变化的内应力如图3所示。

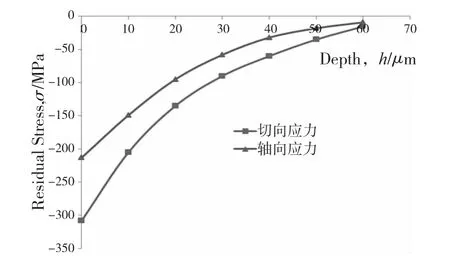
图3 最终测得的随深度变化的切向和轴向内应力

可以看出，在数值上切向的应力大于轴向的应力，在最外表面处，其应力在数值上最大，往深处延伸时两个方向的应力均递减，在深度为60μm处切向和轴向的应力均已趋于0。可以明显看出，加工引起的表面内应力其深度很浅，但是在深度上的变化率很高，这是加工引起的表面内应力的最主要特征。

从以上测量过程可以看出，其测量所需设备价格低廉，且测量过程简单，而Moore and Evans提出M&E修正公式（1）、（2）、（3）需要首先用X射线应力仪逐层测得最外层的应力值，其次需要根据每次测得的值逐层修正应力值，其所需要的设备价格昂贵，X射线法测量过程本身会引入10%的误差，该方法很容易造成误差的积累，而测量应变的过程其准确度是比较高的，从该方面将，本文所描述的方法占有明显优势。

3 基于有限元分析的变形预测

运用以上测得的应力值用有限元法计算其对零件变形的影响。在有限元软件Abaqus中按照零件的实际尺寸和形状进行建模，为便于对模型施加表面应力，根据实际每次腐蚀去除材料的厚度对模型的外表面进行几何元素的划分。实验过程中每次剥层的厚度为10μm，总共剥层的深度为60μm，因此在建立模型时候将外层的60μm平均分成6层，划分网格后模型外表层如图4所示。

图4 模型划分网格后外表面按照指定的深度分层

在给模型施加应力时考虑到在直角坐标系中每个单元的应力是不同的，因此无法通过软件的界面操作给模型施加初始应力，只能通过编写应力文件进行导入的方式给模型施加应力。

在模型的inp文件中，其包括模型所有节点的坐标信息以及与单元相关的节点的编号的信息。将前面测得应力曲线文件进行曲线拟合公式，并根据节点的坐标计算所有节点的受力情况。由于最终应力文件最终只能以单元所受应力的形式进行施加，因此必须将所有节点受力转化为单元所受的应力。这里将单元所受的应力确定为与其相关的节点所受应力的平均值，在软件中编辑关键字，通过关键语句将应力文件导入软件的模型中并进行计算。导入后模型外表层的受力情况如图5所受。

图5 给模型外表层所施加的随深度变化的内应力

可以看到在深度方向应力的变化梯度很大，这是金属切削加工引起的表面内应力的主要特征。通过有限元计算，最终达到自平衡后可以看到零件发生了变形，将变形系数放大后可以看清楚地看到零件的变形情况，如图6所示。

图6 外表层的内应力所引起的零件的变形

在模型的外表面沿轴向作一条路径，用以观察模型外表面在径向和轴向的变形，由于整个模型是环向对称模型，因此观察这条路径上的点位移变化可以说明整个模型外表面的变化情况。

根据路径上所有点的变形位移，最终得到模型的外表面的径向变形和轴向变形，如图7所示。

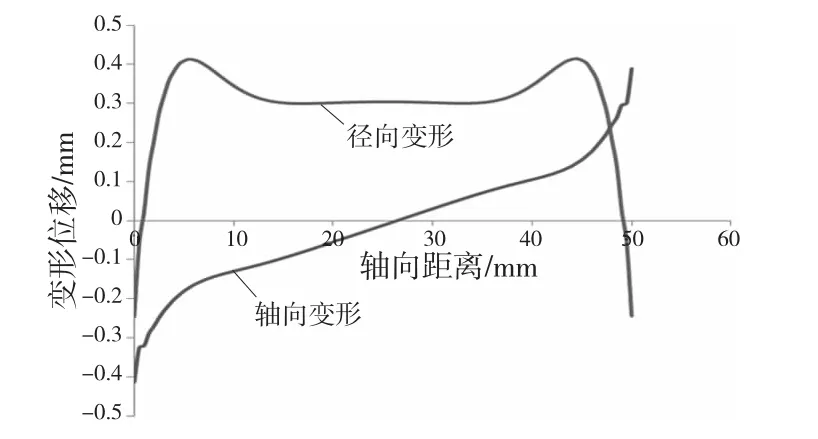
图7 有限元计算得到模型外表面在径向和轴向上的变形

可以看出，表面内应力会引起零件在径向和轴向上产生一定的变形，在两端由于靠近边缘，其边缘效应的影响导致其变形不稳定，最大变形为0.4mm，在轴向中部其径向变形位移趋于稳定；零件的轴向变形两端均往内部收缩0.4mm左右，因此可以看到此加工表面的内应力对该零件的变形的影响是是不可以忽略的，在精度要求高的场合，其对零件变形产生的影响必须考虑。

4 总结与展望

通过化铣剥层和测量零件应变变化的方法，通过计算最终得到了TB2零件表面车削加工引起的随深度变化的内应力，可以看到在切削方向和进给方向上其内应力均呈现压应力的状态，在数值上切削方向的应力大于进给方向的应力，在深度为60μm左右的深度两个方向的应力均已趋于0。将测得的应力施加给有限元模型，通过计算单元的应力并将应力文件通过关键字导入实现应力的施加，最终计算结果表明该内应力对零件的变形产生一定的影响，在精度要求高的场合其变形是不容忽视的。在实际中为消除加工内应力对零件变形的影响，可以采取加工过程中保留很浅的加工余量，使得加工引起的表面内应力留在这一层很浅的加工余量内，在通过化铣的方法去除这一层加工余量，在去除材料的同时去除了切削加工引起的表面内应力，使得零件的精度得到大大提升。

［1］郭世杰，胡志勇，范斌，等.基于ABAQUS的镍基合金加工表面残余应力有限元模拟［J］.组合机床与自动化加工技术，2013（9）；55-58.

［2］苗勇.残余应力对整体结构件加工变形的影响［J］.组合机床与自动化加工技术，2011（9）；81-83.

［3］谢小正，赵荣珍，陈惠贤.高速铣削汽轮机叶片表面残余应力影响因素研究［J］.组合机床与自动化加工技术，2013（11）；15-17.

［4］Larsson C，Holden T M，Bourke M A M，et al.Measurement and modeling of residual stress in a welded Haynes＜sup＞®＜/sup＞25 cylinder［J］.Materials Science and Engineering；A，2005，399（1）；49-57.

［6］Mirzaee-Sisan A，Fookes A J，Truman C E，et al.Residual stress measurement in a repair welded header in the as-welded condition and after advanced post weld treatment［J］. International journal of pressure vessels and piping，2007，84（5）；265-273.

［7］Ficquet X，Smith D J，Truman C E，et al.Measurement and prediction of residual stress in a bead-on-plate weld benchmark specimen［J］.International Journal of Pressure Vessels and Piping，2009，86（1）；20-30.

［8］García Navas V，Gonzalo O，Bengoetxea I.Effect of cutting parameters in the surface residual stresses generated by turning in AISI4340 steel［J］.International Journal of Machine Tools and Manufacture，2012，61；48-57.

［9］Pratihar S，Stelmukh V，Hutchings M T，etal.Measurement of the residual stress field in MIG-welded Al-2024 and Al-7150 aluminium alloy compact tension specimens［J］.Materials Science and Engineering；A，2006，437（1）；46-53.

［10］SebastianiM，Eberl C，Bemporad E，etal.Depth-resolved residual stress analysis of thin coatings by a new FIB-DIC method［J］.Materials Science and Engineering；A，2011，528（27）；7901-7908.

［11］Moore M G，EvansW P.Mathematical correction for stress in removed layers in X-ray diffraction residual stress analysis［R］.SAE Technical Paper，1958.

［12］George D，Smith D J.Through thickness measurement of residual stresses in a stainless steel cylinder containing shallow and deep weld repairs［J］.International Journal of Pressure Vessels and Piping，2005，82（4）；279-287.

［13］孟龙晖，何宁，李亮.TC4管状零件内壁加工残余应力计算及其有限元分析［J］.中国机械工程，2014，25（19）；2583-2587.

（编辑 李秀敏）

The Measurement of the Surface Residual Stresses Induced by Turning in TB2 Parts and the Deformation Prediction Based on FEM

WANG Yi
（College of Engineering，Lishui University，Lishui Zhejiang 323000，China）

；When TB2 parts have been machined，there w ill be high residual stresses induced by machining in the surface layers，the surface residual stresses were calculated based on the changing strains when removing the material layer by layer.As to predict the deformations of the parts caused by the surface residual stresses，the residual stresses values changing along the depth direction should be loaded to the FEM model，and the part is cylinder，the stress value in each element is different，a programing method has been presented in this paper.The stress value of each element can be determined based on the coordinates of the nodes，and the stress values of all the elements can be calculated out.The stress file calculated was loaded to the model，with FEM calculation，the deformation of the part caused by surface residual stresses was calculated at last.

；residual stress；strain；chemical milling；finite element analysis（FEA）

TH161；TG506

A

1001-2265（2015）05-0058-04 DOI：10.13462/j.cnki.mmtamt.2015.05.016

2014-09-13；

2014-11-07

国家科技支撑计划课题资助（2013BAC16B02）

王毅（1980—），男，浙江丽水人，丽水学院讲师，研究方向为数字化制造，（E-mail）jefflsxy@gmail.com。