尺寸参数对3自由度等刚度永磁弹簧力学性能影响研究*

孙兴伟，张 明，孙 凤，张晓友

（1.沈阳工业大学机械工程学院，沈阳110870；2.日本工业大学机械工程系，日本琦玉县345-0826）

尺寸参数对3自由度等刚度永磁弹簧力学性能影响研究*

孙兴伟1，张 明1，孙 凤1，张晓友2

（1.沈阳工业大学机械工程学院，沈阳110870；2.日本工业大学机械工程系，日本琦玉县345-0826）

提出一种3自由度等刚度永磁弹簧。该永磁弹簧由3组环形永磁体和柱形永磁体均匀对称布置构成。根据永磁弹簧的结构，改变永磁弹簧参数进行有限元分析，对径向磁力进行仿真计算。仿真结果表明，随着永磁弹簧的永磁体牌号、柱形永磁体的半径和长度、环形永磁体的长度的增加，弹簧径向磁力增加。随着环形永磁体的平均半径的增加，弹簧径向磁力减小。随着环形永磁体和柱形永磁体间的竖直方向气隙长度的增加，弹簧径向磁力呈抛物线趋势变化。实验验证结果和仿真计算结果基本吻合。

等刚度；永磁弹簧；径向磁力；有限元法

0 引言

永磁弹簧是利用永磁体间的磁力实现金属弹簧性能的磁弹簧，它对提高设备的运转速度与精度，并使设备适应特殊工作环境具有重要意义，特别适合于真空、高速、核电和超洁净等特殊的应用场合。永磁弹簧与金属弹簧相比，不存在产生振动和噪音缺点。由于永磁弹簧是利用永磁体间磁力相互作用，节省了金属材料，降低了成本，又拥有无机械接触、无磨损、功耗低、寿命长、噪音小、无需润滑、不发热等优点，可以取代金属弹簧用于快速机械响应机构［1-4］，例如哈尔滨工业大学的高海波博士将磁弹簧减震器应用于行星轮式月球车的减震系统中，没有严格的密封要求，很好的适应了高度真空的月球表面环境，克服了现有以液体或气体为工作介质的减震器的工作局限性［5］。

在分析了环形永磁体和柱形永磁体及气隙磁导的基础上，提出了一种径向为工作方向的3自由度等刚度永磁弹簧。该永磁弹簧的性能主要是由相互作用的永磁体决定的，影响永磁体间相互作用的因素归纳起来主要有以下几点［6-9］；钕铁硼永磁体的牌号 、环形永磁体和柱形永磁体竖直方向气隙的长度、柱形永磁体的半径和轴向长度、环形永磁体的平均半径和轴向长度。这些因素对磁弹簧力学性能都有不同程度影响。基于此，采用有限元仿真计算的方法，在改变不同影响参数的情况下对永磁弹簧的力学性能进行仿真计算分析。最后采用实验测量的方式对仿真计算结果的有效性进行对比验证。

1 结构及工作原理

作者设计了如图1a所示的3自由度等刚度磁弹簧装置。该装置由上顶盖，下底盖，环形永磁体，柱形永磁体和平面球轴承组成。环形永磁体和柱形永磁体同心，同级相对，每个环形永磁体和柱形永磁体为一组，设置多组，且多组永磁体沿下底盖和上顶盖的中心均匀对称安装于下底盖和上顶盖上。将去掉一个轴承端盖的平面球轴承沿下底盖和上顶盖的中心均匀对称安装在下底盖上。永磁体设置3组，3组是达到稳定支撑和3自由度等刚度的最小组数。永磁体和平面球轴承穿插设置。

如图1b所示平面球轴承支撑上顶盖和下底盖使环形永磁体和柱形永磁体在轴向方向上形成一定气隙，每组永磁体间在竖直方向上表现为吸引力，在水平方向上表现为斥力，这样永磁弹簧的上顶盖和下底盖间在轴向方向上形成一定刚度，上顶盖在轴向方向上不会发生窜动，此种布置的永磁弹簧，在平动平面内，可以沿着x方向，y方向移动和c向转动。沿x方向，y方向移动和c向转动的位移量相等则受到的回复斥力相等，即沿x方向y方向移动和c向回转的刚度系数相等。该永磁弹簧的总回复力为n倍的单组永磁体斥力（如图2a所示），即永磁弹簧的总斥力只与环形永磁体和柱形永磁体相对位置关系有关。总转矩为n倍单组永磁体斥力与半径之积（如图2b所示），环形永磁体与柱形永磁体相对位移增大时，和单组永磁体相对永磁弹簧中心半径增大时，总转矩都增大，即磁弹簧的总转矩不仅和与环形永磁体和柱形永磁体相对位置有关，还和单组永磁体相对永磁弹簧的半径有关。当上顶盖与下底盖沿中心水平方向平动或转动时环形永磁体和柱形永磁体在水平面内的磁力随着位移增大而增大。最大位移量为环形永磁体内半径与柱形永磁体半径的差。

图1 3自由度等刚度磁弹簧结构

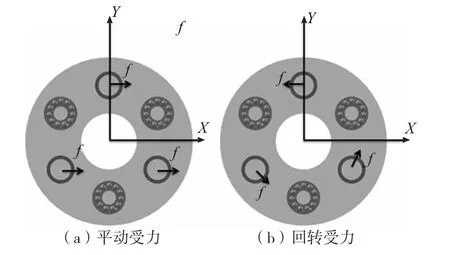
图2 3自由度等刚度磁弹簧受力分析

2 力学性能分析

为了对该永磁弹簧各方面特性进行深入分析。首先建立该系统的结构模型。由于该系统由3组结构完全相同的柱状永磁体和环形永磁体构成。首先建立一组永磁体的模型［7-9］（如图3所示）。

2.1 有限元分析

利用电磁场有限元仿真软件，对该永磁弹簧一组永磁体进行了仿真分析。根据图3和表1中的参数建立的有限元仿真模型［10-11］。

图3 一组永磁体的结构参数

将表1中的参数作为仿真计算的公用值，分别改变永磁体牌号、轴向气隙长度、柱形永磁体半径和轴向长度，环形永磁体平均半径和轴向长度，代入有限元仿真计算，分析径向磁力与这些参数的关系。

2.2 径向磁力与永磁体参数的关系

将N30、N35H、N38、N40、N42不同牌号的钕铁硼永磁材料的参数代入有限元分析模型。结构参数如表1。取轴向气隙z=0.5mm，柱形永磁体和环形永磁体间的径向偏移量e从0变化到5mm，进行有限元分析。径向磁力与钕铁硼永磁体牌号的关系如图4所示，可见，随着钕铁硼永磁铁磁性（Br和Hc）的增强，即永磁体牌号的增加，径向磁力增强，弹簧刚度增大。

钕铁硼永磁材料为N35H，结构参数如表1。柱形永磁体和环形永磁体间的径向偏移量e=2mm，将轴向气隙z从0变化到5mm。代入有限元分析软件得到计算结果。径向磁力与轴向位移的关系如图5所示，径向磁力随着轴向位移的增加呈抛物线趋势变化，在仿真的参数条件下轴向2.5mm处，径向磁力峰值约为2.25N。

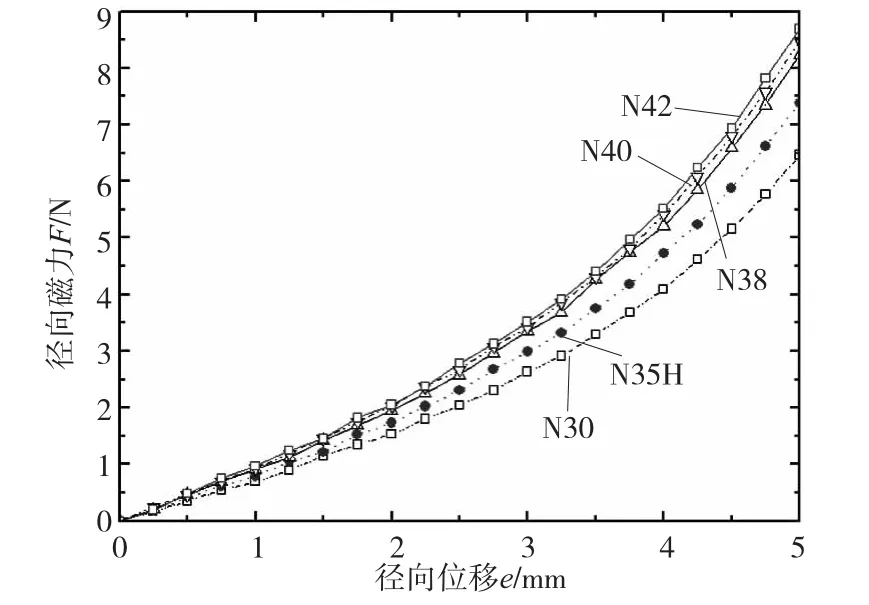
图4 径向磁力与永磁体不同牌号的关系图

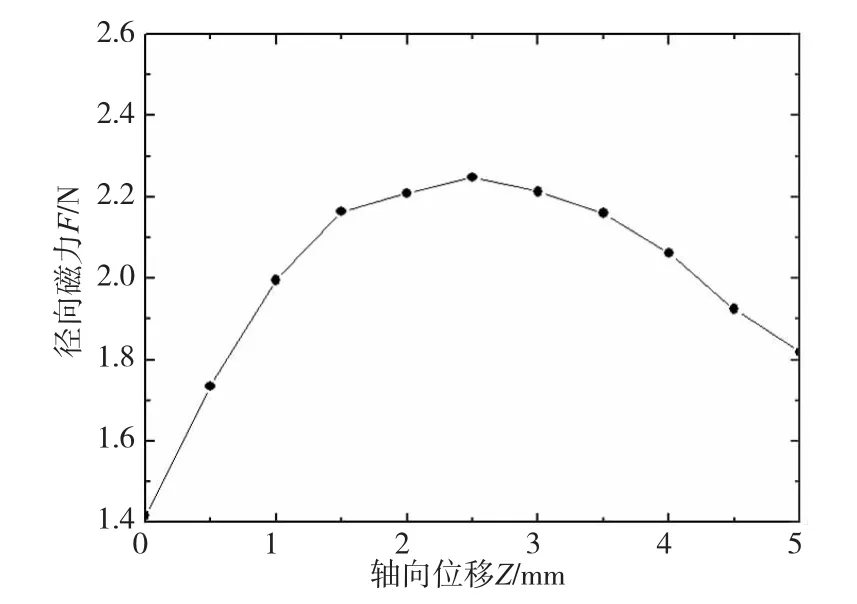
图5 径向磁力与轴向气隙位移的关系图

钕铁硼永磁材料为N35H，结构参数如表1。环形永磁体结构参数不变，柱形永磁体和环形永磁体间的径向偏移量e=2mm，轴向气隙z=0.5mm，将柱形永磁体半径r从7mm变化到12mm，柱形永磁体长度L2从9mm变化到16mm。代入有限元分析软件进行有限元分析。径向磁力与柱形永磁体的半径和长度的关系如图6所示，可见，径向磁力随着柱形永磁体半径的增加近似呈幂指数关系增加。径向磁力随着柱形永磁体轴向长度的增加近似呈线性关系增加，可见在其它参数不变的情况下，柱形永磁体的半径对径向磁力的影响比轴向长度对径向磁力的影响要明显的多。

钕铁硼永磁材料为N35H，结构参数如表1。柱形永磁体结构参数不变，柱形永磁体和环形永磁体间的径向偏移量e=2mm，轴向气隙z=0.5mm，环形永磁体平均半径R=0.5（R2+R1），保持环形永磁体的外径和内径差R2-R1=6mm不变，环形永磁体平均半径R从15mm变化到20.5mm，长度L1从2mm变化到9mm。代入有限元分析软件进行有限元分析。径向磁力与环形永磁体的平均半径和长度的关系如图7所示，可见，径向磁力随着环形永磁体平均半径的增加逐渐减小。径向磁力随着环形永磁体轴向长度的增加近似呈幂指数关系增加，可见在其它参数不变的情况下，环形永磁体的轴向长度对径向磁力的影响比平均半径对径向磁力的影响要明显的多。

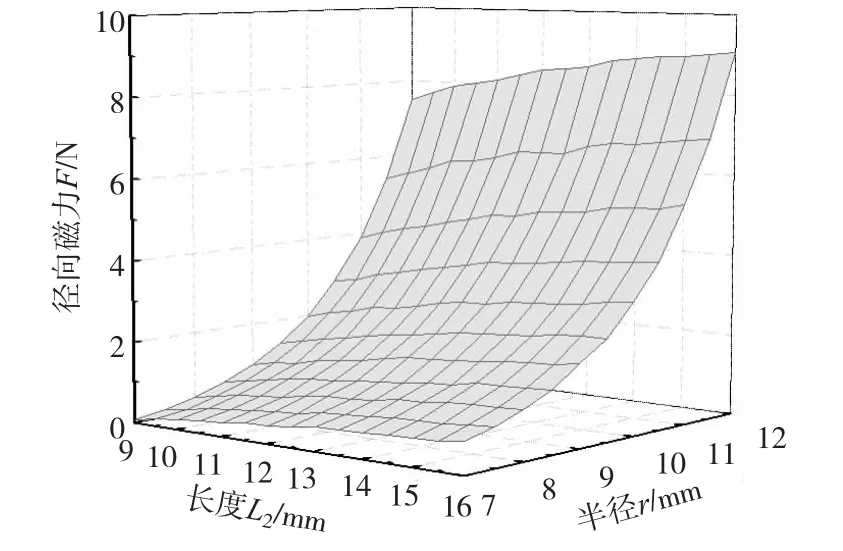
图6 径向磁力与柱形永磁体半径和高度的关系图

图7 径向磁力与环形永磁体平均半径和高度的关系图

3 实验验证

试验台照片见图8。图中，1为z向一自由度微动平台，量程为13mm，精度为0.01mm；2为铝合金型材搭建的龙门框架；3为力传感器，型号为Load Cell CXZ -114，量程为0～300N，精度为0.01N；4为柱形永磁体；5为环形永磁体；6为xy方向两自由度微动平台，量程为13mm，精度为0.01mm；7为力值显示控制仪，型号为XSB-I。xyz3个方向的微动平台可以实现柱形永磁体和环形永磁体的对中，可以从微动平台上读出径向相对位移量，从力值显示控制仪上读出径向磁力。

实验条件如下；环形永磁体外径R2为20.5mm，环形永磁体内径R1为14.5mm，柱形永磁体半径r为9mm，环形永磁铁长度L1为4mm，柱形永磁铁长度L2为14mm，永磁体材料NdFeB N30，永磁体剩磁Br为1.12T，永磁体矫顽力Hc为796000 A/m，空气磁导率μ0为4π×10-7H/m，（BH）max取223kJ/m3，柱形永磁体和环形永磁体间的轴向气隙z=0.5mm、将径向偏移量e从0变化到4mm每次增加0.25mm。得到径向磁力的实验值。如上条件的实验结果与相同条件下的仿真结果对比呈现于图9。由图9可以看出，在上述实验条件下，永磁弹簧的径向磁力随径向位移增加近似呈线性关系关系增加。大径向偏移时误差偏大，这主要是由环形永磁体和柱形永磁体间实际漏磁随径向位移增大而也越来越大。

图8 径向磁力测量实验台

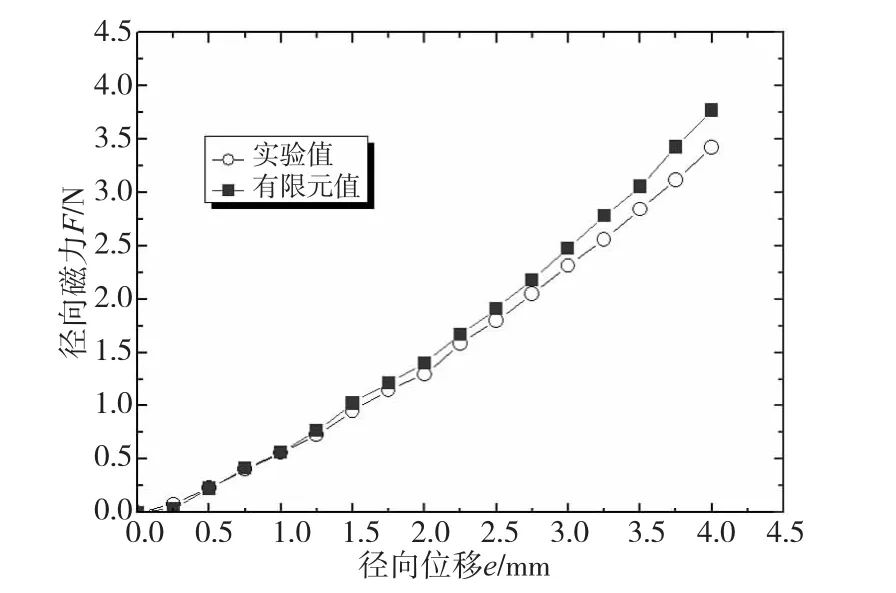
图9 径向磁力实验与仿真对比图

4 结论

采用有限元分析与实验验证相结合的方法，分析了不同尺寸参数对3自由度等刚度永磁弹簧的力学性能影响情况，分析结果表明；该型永磁弹簧的径向磁力随永磁体的牌号的增加、柱形永磁体的半径和轴向长度的增加、环形永磁体的轴向长度的增加，弹簧径向磁力增加。随着环形永磁体的平均半径的增加，弹簧径向磁力减小。随着环形永磁体和柱形永磁体间的竖直方向气隙长度的增加，弹簧径向磁力呈抛物线趋势变化。此永磁弹簧的非接触及等刚度特性非常适用于高速及超洁净等工业应用领域。

［1］Kun-XiQian，Pei Zeng，Wei-Min Ru，et al.Novel Magnetic Spring and Magnetic Bearing［J］.IEEE Transactions on Magnetics，2003，39（1）；559-561.

［2］Will Robertson，Ben Cazzolato，Anthony Zander.A Multipole Array Magnetic Spring［J］.IEEE Transactions on Magnetics，2005，41（10）；3826-3828.

［3］孙凤，张明.三自由度等刚度磁弹簧［P］.中国；ZL201420083637.7.2014，02，06.

［4］刘雪箐，白志红，熊光煜.永磁弹簧的设计与计算分析［J］.太原工业大学学报，2004，35（3）；349-351.

［5］高海波，邓宗全，胡明，等.行星轮式月球车移动系统的关键技术［J］.机械工程学报，2005，41（12）；156-161.

［6］于慎波，姜菲菲，王辉，等.永磁同步电主轴分数槽电机的径向电磁力分析［J］.组合机床与自动化加工技术，2014（6）；15-18.

［7］张云鹏，刘淑琴，李红伟，等.基于磁路分析的轴向混合磁轴承径向承载力解析计算［J］.电工技术学报，2012，27（5）；137-142.

［8］汤双清，蔡敢为，杨家军，等.一种新型被动磁悬浮轴承的研究［J］.中国机械工程，2002，12（2）；2134-2136.

［9］田录林，李言，安源，等.轴向放置轴向磁化的双磁环永磁轴承径向磁力研究［J］.机械工程学报，2007，18（24）；2926-2929.

［10］王昆，张弓，刘强.基于Ansoft/Maxwell新颖电机三维有限元优化分析［J］.组合机床与自动化加工技术，2014（5）；58-61.

［11］赵博，张洪亮.Ansoft12在工程电磁场中的应用［M］.北京；中国水利水电出版社，2010.

（编辑 李秀敏）

Study on Influence of Size Parameters on Mechanical Characteristics of 3 DOF Same-stiffness Permanent Magnetic Spring

SUN Xing-wei1，ZHANG Ming1，SUN Feng1，ZHANG Xiao-you2
（1.School of Mechanical Engineering，Shenyang University of Technology，Shenyang 110870，China；2.Department of Mechanical Engineering，Nippon Institute of Technology，Saitama 345-0826，Japan）

；This paper proposes a 3 DOF same stiffness permanent magnetic spring.This permanent magnetic spring consists of 3 pairs of annular permanent magnets and cylindrical permanent magnets which are arranged uniform ly and symmetrically.According to the structure of permanent magnetic spring，the simulation radial magnetic force is carried out by finite element method by changing size parameters.The simulation results show that radial magnetic force increases with the increasing of permanent magnetic type，the radius and axial length of cylindrical permanent magnetand the axial length of annular permanent magnet.The radial magnetic force decreases with the increasing of the averaged radius of annular permanent magnet.The radial magnetic force changes in parabolic trend along with the increasing of air gap length between annular permanent magnet and cylindrical permanent magnet.The simulation results are basically in agreement with the experimental results.

；same-stiffness；permanent magnetic spring；radial magnetic force；finite-element method

TH135；TG659

A

1001-2265（2015）05-0010-04 DOI：10.13462/j.cnki.mmtamt.2015.05.003

2014-08-21；

2014-09-19

国家自然科学基金资助（51105257）；辽宁省博士启动基金资助（2011042）

孙兴伟（1970—），女，沈阳工业大学教授，博士，研究方向为复杂曲面数控加工与控制技术等，（E-mail）sunxingw@126.com；通讯作者；

张明（1988—），男，沈阳工业大学硕士研究生，研究方向为机电系统控制与优化，（E-mail）zm201234@hotmail.com。