教学中渗透“化归思想”的探索
2015-11-01福建省福州市岳峰中心小学黄丽丽
◎福建省福州市岳峰中心小学 黄丽丽
教学中渗透“化归思想”的探索
◎福建省福州市岳峰中心小学黄丽丽
“化归思想”是一种重要的数学思想方法。数学教学的任务就是要把隐含在知识体系中的化归思想加以揭示,将其渗透落实到每一个学段的数学课堂和数学活动中,进而发展学生数学思想能力。
化归思想;整体把握;有效渗透;精心预设
数学教师在日常教学中,要扣紧“化归”这根弦,把隐含在知识体系中的化归思想加以揭示,以便引导学生运用化归思想,将一个非基本的问题通过分解、变形、代换、平移等多种转化方式,归结为一个熟悉的基本的问题,实现复杂问题简单化、抽象问题直观化、未知问题已知化,从而使问题得到解决。学生在学习的过程中要感悟、体验、运用化归思想,提升数学素养。
一、系统研读整体把握
知识有形,而思想却无形。数学知识以“白纸黑字”的具象形式呈现在数学教材中,而数学知识体系中所蕴含的数学思想,却隐藏在教材的每一个章节中,体现在揭示、应用知识的过程中。因此,教师必须仔细研读每一册教材、每一个章节、每一道例题,系统地对教材文本的编排体系进行梳理,充分挖掘小学各年级、各章节数学教材中所蕴含的化归思想的脉络,使化归思想的渗透成为一种有意识的、自觉的教学活动。下面以人教版新教材为例来分析化归思想在解决实际问题中的应用。
1.数与代数领域。以整数、小数、分数、负数的意义编排为出发点,首先通过直观图像、数轴、实物操作等学习整数加减乘除法,实现复杂问题简单化、抽象问题直观化,从而渗透化归思想;然后扩展到小数加减法、乘除法,这些知识分布在小学阶段的每一册教材中,形成完整的知识体系。
2.空间与图形领域。在第一学段,通过拼摆面积为1cm2的小正方形推导出长方形的面积,这是所有平面图形面积学习的基础。第二学段平面图形面积的学习,是建立在第一学段学习的基础上,通过剪拼成长方形推导出平行四边形的面积;继而推导出三角形、梯形、圆的面积。整个过程都借助于化归思想,把未知问题以已知化呈现,构成整个平面图形面积的学习体系。学生系统地学习了平面图形的面积后,可以为后续组合图形面积的学习奠定坚实的基础。化归思想作为最基本的思维策略,随着学生年级的升高而形成一种习惯的数学思维方式,不断把复杂的问题简单化。如图①,求组合图形的面积。学生根据自己的需求,将组合图形分解为基本图形:可以分解为2个梯形,也可以分解为长方形和三角形。分别求出基本图形的面积,再算总面积,这就是化归思想的应用。
图①
3.在统计与概率领域。用直观的线段、图表等来表示抽象数量之间的关系,这种化归思想,不仅能使抽象的数据具体化,还能培养学生对未知事物的判断、预测策略的生成。而在综合与实践领域,旨在培养学生灵活地用化归思想解决问题。
上述例子只是管中窥豹,未及全貌,但隐藏在点滴数学知识中的化归思想,却作用于数学学习的方方面面。教师必须细心研读教材,在重视显性的数学知识教学的同时,也重视隐藏的化归思想整体递进的探索过程,使所构建的数学知识,做到点面结合,纵横交错,形成立体的数学思想网格,进而实现化归思想培养的整体提升,帮助学生深刻认识到数学知识之间的紧密联系。
二、分层培养有效渗透
不同年龄阶段的学生有不同的思维特点,不同的知识也有不同的结构特征和不同的思想方法,各种数学思想方法的培养也不是一蹴而就的。随着年级的升高,在不断地增加化归思想的深度和广度上,结合丰富的数学活动有效地渗透是至关重要的。
图②
1.第一学段:感知、体验
这一学段学生的思维是以具体形象思维为主,教师可创设具体感性的数学问题情境,引导感知、初步体验化归思想。如:1-10的认识(图②),教材呈现的是数形结合,从实物、数小棒出发,再到数的认识,学生体验的是抽象问题具体化的化归思想;学习10以内的加减法的加法计算时,把大数放在心里,小数是几就把大数再往后数几,呈现的是复杂计算简单化的化归思想;到了20以内的加减法就是利用10以内加减法的知识迁移解决,是使未知问题已知化的化归思想有了进一步的递进。有了一年级的感悟和体验,到了二、三年级再不断地感知、体验,化归思想就烙在学生心中,学生自然就能利用化归思想解决较为复杂的数学问题。
2.第二学段:领悟、运用
这一学段学生的思维较之第一学段产生了质的飞跃,教师可直接介绍化归思想,采用抽象的文字表述,使学生进一步领悟自己所使用的方法,从更深层次上感悟化归思想,运用化归思想解决简单的实际问题。如五年级上册《小数乘整数》中的例1,一个风筝3.5元,买3个要花多少钱?教师应让学生自主学习教材,理解文本呈现的三种方法所蕴含的思维元素:①用3个3.5连加;②把3.5元转化成3元5角,分别求出3个3元和3个5角,再合并起来;③把3.5元转化成35角,也就是扩大到原来的10倍,乘3是105角,最后再把积还原,转化为原来的十分之一。学生一下子反应过来,这是把新知识转化为以前学过的旧知识解决。这三种方法都渗透了化归思想,但在层次上有递进,方法上有变化,思维的质量上有提高。
三、精心预设贯穿始终
化归思想是以数学知识为载体得以显化的。化归思想的提炼、归纳和概括,伴随着数学知识学习的过程,贯穿整个课堂教学的始终。课堂上,教师将数学知识所蕴含的数学思想内化为自己的教学思想,外化在每一节课堂教学中,预设到每一个教学细节,有始有终地渗透化归思想。如人教版数学三年级上册《万以内的加法和减法》中的例1、例2:一共要买几张车票?口算两位数加两位数(不进位、进位)的加法时,教师根据学生的知识最近发展区和教材编排特点,运用了三个策略来渗透化归思想:
策略之一:揭示
上课伊始,教师和学生分享了“曹冲称象”的故事,并揭示:聪明的曹冲就是运用了化归思想,用石头的质量代替大象的质量,从而解决了问题。同时出现框图(图③),让学生体验化归思想的妙用。以一个熟悉的小故事作为教学资源,有效地利用,使得导入环节不但有了数学味儿,更蕴含着数学思想,让数学的简约之美极致绽放。
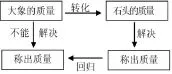
图③
策略之二:运用
有了导入的铺垫,思维敏捷的学生就有想法了:“老师,这节课我们是不是也要像曹冲那样用到化归思想啊!”“那就得看看你们爱不爱动脑筋了!”教师引而不发,顺势出现了例1:秋游的情境(图④),教师有意识地引导学生利用收集的数学信息,提出用加法解决的数学问题:一共要买几张车票?(35+34)

图①
“你能解决吗?有几种计算的方法?”如果说第一个问题的解决是顺理成章的,那么第二个问题的出现就是一项挑战了。学生在独立思考之后,又进行互相交流,在集体汇报时,学生大胆提出了三种算法:
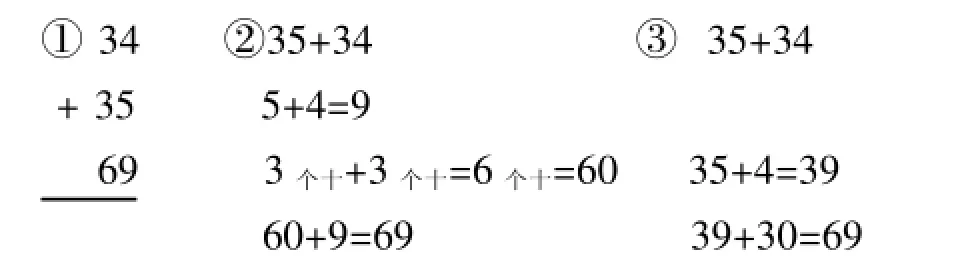
当这几种方法都书写在黑板上时,就有学生发现,可以用以前学过的知识解决。是的,其实二年级教材在《100以内的笔算加法和减法》中就有所呈现,但两位数加两位数的口算,学生并没有系统地接触过。这时,教师因势利导:“同学们,你们已经学会运用化归思想解决数学问题啦!《万以内的加法和减法》是新知识,你们把没有学习过的新知识转化为已经学过《100以内的加法和减法》,从而解决了问题!有智慧的孩子!你们和曹冲一样聪明!”
(边说边用框图表示,再次渗透化归思想。)
教师的激励犹如投入油锅中的水,激发了三年级孩子的学习热情。在出现例2:一共要买几张车票?口算39+44时,学生除了模仿刚才例1的三种方法外,还想到了一年级学过的“凑十法”,让口算更简单:39+1+43 44+6+33。这为后续简便计算的学习奠定了基础。
本课的知识点对于三年级的学生来说没有什么难度,但隐藏在知识背后的化归思想却在学生的思考、探究、交流中得以渗透,实现内化。教师的“化归”眼光和“化归”意识,往往决定着数学课堂教学的品质,决定学生思维的可持续发展。
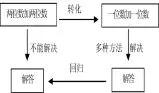
策略之三:提炼
通过这样的一堂课,学生不仅学会了知识的归纳和整理。更学会用旧知识来解决新问题。而教师利用框图对数学学习方法进行回顾和总结,进而对化归思想的提炼,起到“画龙点睛”的效果,有效地将化归思想内化为学生的自身需求,提升其数学素养,学生由此感知化归思想的妙处,并学会了主动运用。
(责任编辑:陈志华)
