面向准时生产的第三方物流货物配装优化
2015-11-01分析人杜彦炜
分析人:杜彦炜 吴 照
面向准时生产的第三方物流货物配装优化
分析人:杜彦炜 吴 照
为了适应制造企业准时化生产方式,第三方物流企业在配送货物时,要及时响应订单,提高供货频次,准时为生产供货。本文应用容重比启发式算法进行配装优化实施,综合考虑车厢容积、载重量约束条件来确定所装货物的种类和数量。实例证明,应用该算法使车厢的容积和载重量均能得到很好的利用。
随着客户个性化需求不断增加和所要求交货期的缩短,制造企业传统的批量生产方式已经不能适应多品种变批量的生产订单。而基本思想为“在所需要的时刻,按所需要的数量生产所需要的配件”的准时化生产方式成为制造企业盛行的生产模式。为了适应制造企业准时化生产方式,第三方物流企业在配送货物时,要对订单进行快速识别和分类,充分利用车辆的载重量和容积,合理安排货物装载作业,短时间内制定出与客户要求相适应的配装方案。本文针对单车多品种货物配装优化问题,采用容重比启发式算法确定所装货物的种类和数量,从而克服了以往依靠经验制定配装方案的缺点。
多品种货物配装问题
多品种货物配载优化是指给定了一批待装长方体货箱和长方体容器,按一定的要求将待装货物互不干涉地摆放在这一容器内,使某一项或几项性能达到最优。该问题的优化可归结为一类离散组合优化问题。如何制定出一个合理的装载方案,以在保证装运的顺序、重量限制、装箱效率等条件约束下,使该容器的空间利用率最大,是这类问题的主要目标。对多种物资配载优化问题的研究方法有启发式算法、智能搜索方法(如模拟退火算法、禁忌搜索算法、蚂蚁算法、遗传算法)、穷举法、动态规划法以及图论法等。智能搜索方法比较适合于解大规模组合优化问题。启发式算法在目前处理多种物资配装问题时被广泛应用,它凭借有效的优化策略来减小搜索空间的规模,从而缩小搜索范围,尽可能在很短的时间内找出问题的最优解,具有很强的实用价值。
配装优化模型
将单车多品种货物配装描述为:某车辆对N种货物配装,最大程度利用单辆货车的容积及载重量,确定所装货物的品种和数量,在尽可能满载的条件下获得最大经济收益。
有n个具有不同尺寸和重量的货物,1个容积为V、载重量为W的运输车,要求利用车辆的容积及载重量。
前提条件:
(1)每件货物的体积和重量比车厢的容、载重量小;
(2)货物为直送即送往同一地方;
(3)假设所有货物都不相同(实际情况同种货物可归为一种);
优化模型为:
约束条件:

式中xi⊂{0,1},xi=0时表示不装货物,xi=l时表示装入货物i ,wi代表货箱i的重量,vi代表货箱i 的体积;λ⊂(0,l),λ=l时,目标为载重量最大,λ+µ=l; µ=1时,目标为容积利用率最大。
若求得的最优解形式为(l,0,1,0,l,l,0,0),则表示所要装载的货箱编号为l,3,5,6,其余不装在本车上。
容重比启发式算法求解
算法思想
容重比算法是指如果已装载的货箱的容重比与车厢的容重比接近时,则已装载货箱的重量与车厢的载重量接近,已装载货物的体积和车厢的容积接近,说明充分地利用了车厢的载重及容积。
设某货箱的重量为W,货箱的体积为V,称VW为该货箱的容重比。
设货箱集合为N=(1,2,3…n),货箱对应的重量集合G=(w1,w2,w3…wn) ,货物对应的体积集合V =(v1,v2,v3…vn),ci=viwi为第i个货物的容重比,所有货物的容重比集合为R=(c1,c2,c3…cn),S0=V/W为车厢的容重比。
实例
某第三方物流企业接到某机床制造车间一项准时物流配送任务,订单中包含下列14种配件,分别采用矩形货箱包装,重量和体积信息如表1所示,货箱尺寸分别为:A配件(520×900×1130),B配件(8 0 0×8 0 0×1 7 7 0),C配件(923×871×885),D配件(1000×1000×1000),E配件(812×820×815),F配件(1312 ×932×1175),G配件(1107×869×1254),H配件(632×420×571),I配件(1320×583×720),J配件(1207×190×1096),K配件(512×512×1.54),L配件(870×420×837),M配件(1410 ×832×875),N配件(912×733×1321)。轻卡货车的载重量为300kg,车厢(2818×1394×1806)/㎜,容积为7m3,要求制定出合理的配装结果。
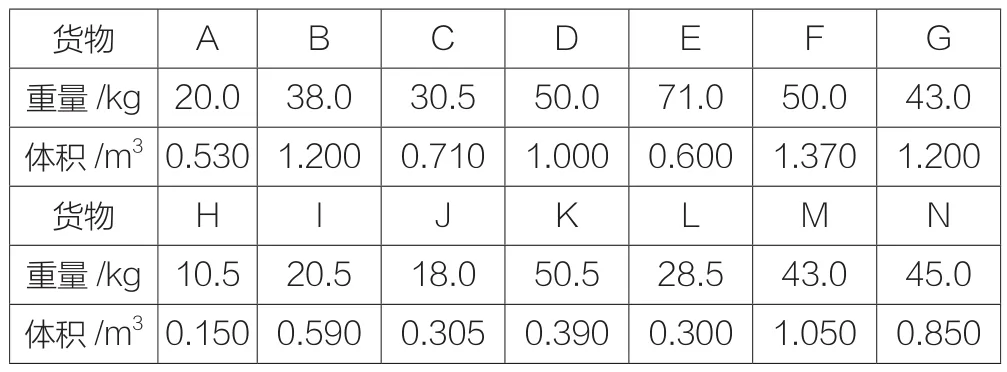
表1 订单中各配件货箱重量和体积
算法求解:
(1)第i 种货物的容重比:ci=viwi得到14种货箱的容重比分别为:
(2)依据货物体积为优先级判断条件,体积越大,优先级越高,经过优先级排序得到集合

对应新的重量集合
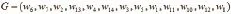
新的体积集合

(3)规定货物B为必须要装入的货物,此时R0=3, T=(6,7,2),Rj+1〈3,得到, N=T ∪N1;
(4)N1中的待装货物容重比ci=viwi货物集合N1中货物的容重比ci=viwi为第i个货物的容重比。
得到剩余货物的容重比集合并按递增顺序排列C1=(cj,cj+1…cj+n)按增序排序的到集合

(5)则已装货物的容重比为:

(6)由于S1>S0,则从待装货物中选取第一个满足下列条件的货物:得到

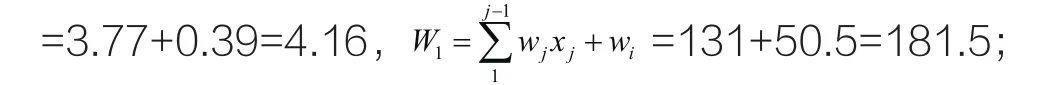

(8)由(7)得已装货物的容重比:

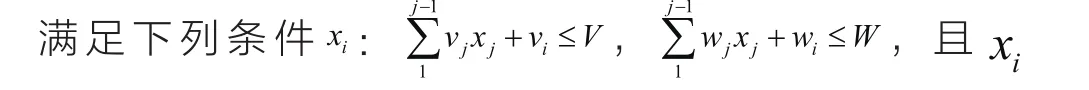
(9)满足第六步的xi不存在,寻找带装货物中可以得到只有x8满足条件,此时已装货物的体积和重量分别为:

(10)因此求得剩余空间和重量为:V剩=V-V1=7-5.62=1.38。W剩=W-W1=300-293.5=6.5;
(11)现在空间已经无法再装入其他货物。则优化后的要装载的货箱见表2

表2 配装优化结果
由表2可计算出装载货物的总体积为5.62m3,装载货物的总重量为293.5kg,载重利用率为98.57%,体积利用率为80.81%。
小结
容重比启发式算法适用于第三方物流企业提供的准时化物流配送,能够方便快速获得比较满意的配装效果,提高了车辆的空间利用率,降低了企业的配送成本,节省了整个配送流程的时间,保证了及时供货,提高了客户的满意度,增强了企业的竞争力。
10.3969/j.issn.1001-8972.2015.09.041
