基于图像强度最优的SAR高精度运动补偿方法

胡克彬　张晓玲　师　君　韦顺军

（电子科技大学电子工程学院　成都　611731）

基于图像强度最优的SAR高精度运动补偿方法

胡克彬*张晓玲师君韦顺军

（电子科技大学电子工程学院成都611731）

由于载体平台的不稳定性和测量传感器的精度限制，运动误差成为了提高合成孔径雷达（SAR）成像质量的一个瓶颈。基于图像锐度最优的自聚焦后向投影算法通过估计相位误差进行运动补偿，具有较高精度，但这种方法假设场景中所有像素点相位误差相同，即没有考虑运动误差的空变性，导致大部分像素点仍存在残留误差，造成成像质量下降。针对运动误差空变性的问题，该文提出一种高精度运动补偿方法，该方法在图像强度最大准则下，采用最优化技术估计天线相位中心测量误差，随后利用该测量误差估计量校正天线相位中心并进行后向投影成像。由于估计天线相位中心等效于估计每个像素点的距离历史，因此该方法可以对每个像素点进行高精度相位补偿。点目标仿真和实测数据处理结果均验证了所提方法的有效性。

合成孔径雷达（SAR）；高精度运动补偿；自聚焦后向投影；空变性

1　引言

合成孔径雷达（Synthetic Aperture Radar，SAR）［1］具有全天候、全天时的对地观测能力，其获得的高分辨微波图像已经被广泛应用于诸多领域，如生成数字高程图、观测火山活动和洪灾情况、监测陆地和海洋交通等［2］。

SAR能得到广泛应用，最根本的前提和最重要的要求是获得高分辨、高质量的微波图像。SAR成像算法主要分为两类：一类是频域成像算法；另一类是时域成像算法。应用最广泛的频域成像算法有距离多普勒算法（Range Doppler，RD）［3］、频率变标算法（Chirp Scaling，CS）［4］和波数域算法（Omega-K，ωK）［5］。所有的频域成像算法都通过快速傅里叶变换（FFT）来达到快速成像的目的。但是，为了利用FFT，不得不对回波模型进行多项式近似，这就造成了成像质量下降。典型的时域成像算法为后向投影算法（Back Projection，BP）［6，7］，其最大的特点是没有任何近似处理，从而理论上可以达到精确成像的目的。然而，载体平台的振动［8］、风场［9］以及湍流［10］都会造成非线性的天线相位中心（Antenna Phase Center，APC），而非线性的APC又严重影响BP算法的性能。因此，在BP成像时必须认真考虑运动补偿的问题。

对于BP成像的运动补偿，目前主要有两类典型的方法。最普遍的方法是利用惯性测量单元（Inertial Measurement Unit，IMU）［11－14］获得的天线姿态信息进行运动补偿，可IMU系统的多种误差仍将影响成像质量［11］。虽然更高精度的IMU被陆续设计出来［12，13］，IMU内部系统误差矫正技术也卓有成效［14］，但随着对成像分辨率和成像质量要求的不断提高，IMU测量精度可能仍然无法满足高精度运动补偿的要求。自聚焦是另一类新的BP运动补偿方法。其中，文献［15］提出的一种自聚焦BP算法（下文用“ABP”特指该算法），该算法通过最优化图像锐度指标来估计每个方位时刻的相位误差，进而进行相位补偿。但我们注意到，ABP算法利用估计获得的一个方位时刻的相位误差去补偿成像空间中的所有像素点，忽略了运动误差的空变效应。这样，剩余相位误差可能导致很多像素点仍然散焦。ABP算法的另外一个缺点是巨大的内存需求，因为它要求存储成像空间中每个像素点在每个方位时刻的后向投影值。

针对ABP算法的上述两个缺点，本文提出了一种适用于BP算法的高精度运动补偿方法。在本文方法中，我们以图像的强度作为目标函数，通过最优化技术估计出每个方位时刻的APC测量误差，然后利用矫正后的APC再进行BP成像。因为估计APC等效于估计每个像素点的相位误差，所以该方法可以获得比ABP算法更加精确的运动补偿。另外，由于新方法不需要存储每个方位时刻的后向投影值，因此对内存的需求大大减少。

本文内容安排如下：第2节详细分析了运动误差的空变特性，并讨论了ABP算法存在的缺陷；第3节建立了APC误差估计模型，然后详细推导了目标函数的梯度；第4节通过点目标仿真和实测数据处理验证了本文方法的有效性。

2　问题分析

ABP算法［15］估计的相位误差向量为：

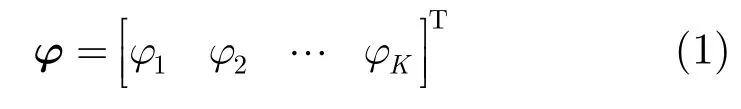
其中，K表示慢时刻数。

BP算法的第1步是将图像空间离散化为像素点网格，对于2维SAR图像，图像空间为2维网格，但是为了方便推导，将2维图像网格用1维向量表示，即2维图像中的像素点以行为优先顺序编号为1，2，…，m，…，M 。如果成像空间中第m个像素点在第k个慢时刻的后向投影值表示为，则第m个像素点相位补偿后的复图像值为：

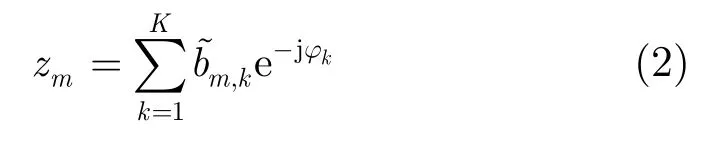
其中，m=1，2，…，M，M表示图像空间中总的像素点个数。

从式（2）可以看出，估计出的相位误差φk用来补偿了场景空间中所有像素点，即ABP算法假设每个像素点具有相同的相位误差，而忽略了运动误差的空变特性。这个假设可以简化相位误差估计问题，但却降低了运动补偿精度。

下面我们用点目标仿真来量化地分析运动误差空变性对运动补偿的影响。考虑两个点目标，包含运动误差的SAR几何示意图如图1所示。

图1中，pi和pa分别表示在同一方位时刻，平台匀速直线运动条件下的APC和平台的真实APC。pω1和pω2分别为场景空间中两个不同像素点的位置，其中pω1被选为参考点。ri1和ri2分别为pi到pω1和pω2的距离，即

图1　含有运动误差的SAR几何示意图Fig.1　Geometry of SAR with motion errors

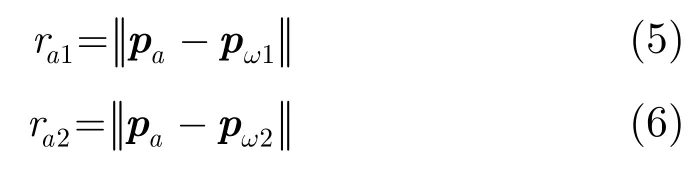
对于像素点pω1和pω2，真实距离和理想距离的绝对误差为：

如果对参考像素点pω1估计出的相位误差用来补偿pω2的相位，则补偿误差以波长λ为单位表示为：

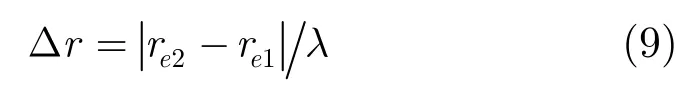
图2展示了量化的补偿误差。每条曲线分别表示真实APC pa在高度向上偏离理想APC pi（高度4 km）的距离，Δh=λ，4λ，7λ，10λ。图2（a）表示随着非参考点pω2与参考点pω1=［3，0，0］km在距离向相距越远时的相位补偿误差，而图2（b）则表示相位补偿误差与两点方位向距离的关系。可以看出，虽然两点方位向的偏离对相位补偿精度影响不大，但距离向的偏离则影响巨大：当目标在距离向上偏离仅150 m，而APC高度误差仅为10λ（λ=0.03m）时，相位补偿误差已经达到0.14λ，这个误差量已超过λ/8，足以让非参考目标散焦。另外，随着两点距离向偏离增大，相位补偿误差近乎线性地增大。由此可知，对高精度成像，运动误差的空变性绝不能忽略。

我们还可以从式（2）发现ABP的另一个缺陷，即每个像素点对应每个方位时刻的后向投影值需要被存储，存储量为K×M×2×8 Byte，特别是对于大场景和长孔径SAR成像，ABP算法对处理器提出了太高的内存要求，以至于在大多数情况下不具有实用性。

3　天线相位中心估计方法

从第2节我们看到对每个像素点分别进行相位补偿的必要性，但是ABP算法忽略了运动误差的空变性而不能获得高精度的运动补偿效果。为了解决这个问题，一种思路是对每个像素点的相位误差分别建立模型，但是这样会把问题复杂化，使得解空间维数变为K×M，而ABP的解空间维数才为K。如果采用迭代算法来求解，成像效率将极大降低。

事实上，对于BP算法，最重要的是获得精确的APC，如果APC的精度能得到满足，就能克服运动误差的空变问题，因为运动误差的空变性本质上就是由APC误差导致的。因此，我们直接估计APC误差，而不是相位误差。这种方法的好处之一就是解空间维数（K×3）相比于ABP不会增加太大；另一个好处在于我们不用再存储每个像素点在每个慢时刻的后向投影值，因而可以大大节约内存开销。

本节首先以SAR复图像强度为目标函数，建立APC误差估计模型；然后利用快速收敛的共轭梯度法求解该模型，因此还详细推导了目标函数的梯度；最后给出了算法流程。

3.1APC误差估计模型

距离压缩后的回波信号可以写为：

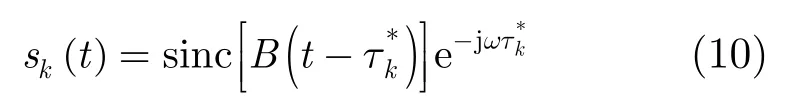
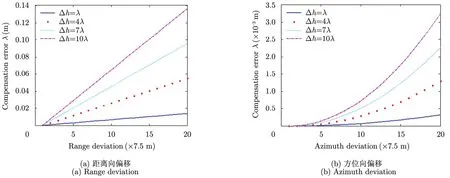
图2　补偿误差与点目标间距关系图Fig.2　Compensation error viatargets distance

其中，τm，k是通过APC误差Δpa，k校正后的回波延迟，即

从式（10）～式（12）可以看出，bm，k的幅度（sinc函数）和相位中均含有APC误差Δpa，k，其中，幅度中的Δpa，k使得后续梯度推导过程极其复杂。因此，我们假设APC误差Δpa，k对后向投影值的影响仅限于一个距离单元内，即忽略运动误差对包络的影响，则bm，k的幅度与APC误差相互独立，bm，k可以写为：

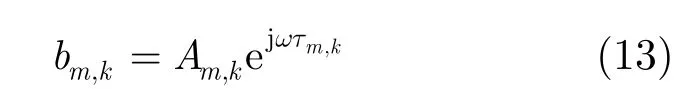
其中，Am，k是第m个像素点在慢时刻k时经测量APC计算出的后向投影值

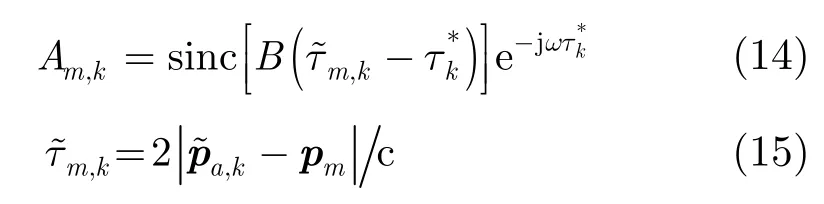
注意，因为测量APC为已知的不变量，在上述假设条件下，不管APC误差为多少，一个像素点在一个慢时刻的后向投影值幅度为常量。将所有K个慢时刻对应的bm，k累加得到第m个像素点总的后向投影值为：

我们最终的目标是确定一种能反映图像聚焦的指标，然后通过调整APC误差优化这个指标，从而获得APC误差估计。ABP算法选用“锐度”作为图像聚焦指标，这里，我们选择“强度”（锐度为强度平方），因为SAR图像聚焦越好，表明每个方位时刻后向投影值的相干性越强，累加后图像锐度或强度就越大，即，同“锐度”一样，“强度”同样可以正确反映SAR图像聚焦效果。除此之外，选择“强度”作为优化指标，可以简化目标函数梯度的推导。

第m个像素点的图像强度fm定义为：

如果所有K个APC误差组成一个向量

则整幅图像的强度即可表示为：

最后，我们得到在最大图像强度准则下估计APC误差Δpa的优化模型为：

3.2目标函数梯度推导

从式（18）可以看出，最优化问题式（20）的解空间维数为K×3，随着合成孔径长度增加而增加。为了加快迭代算法的收敛速度，我们采用共轭梯度法［16］来求解模型式（20）。

在共轭梯度法中，目标函数的梯度必须显式地给出，目标函数梯度为：

从式（19）和式（20）可以看出，求目标函数梯度，其实就是求fm关于所有Δθk（θ=x，y，z ）的偏导数，即

然而，从式（16）和式（17）可知，fm是两个和式的乘积，其导数很难求得。为了简化求导难度，我们将fm重写为：

其中，Rm和Im分别为zm的实部和虚部，即

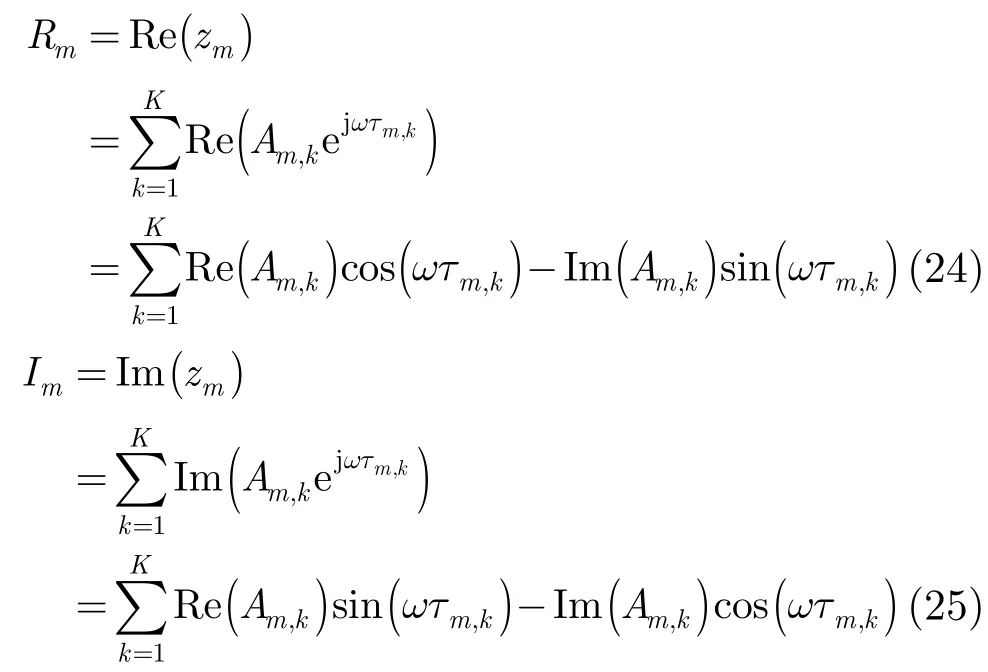
在式（24），式（25）中，Re（·）和Im（·）分别表示取复数实部和虚部运算。

由式（23），式（24）和式（25）可以求得偏导数（∂fm）/（∂Δθk）为：

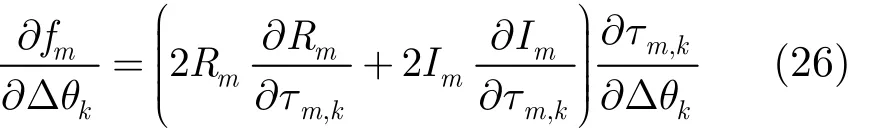
其中

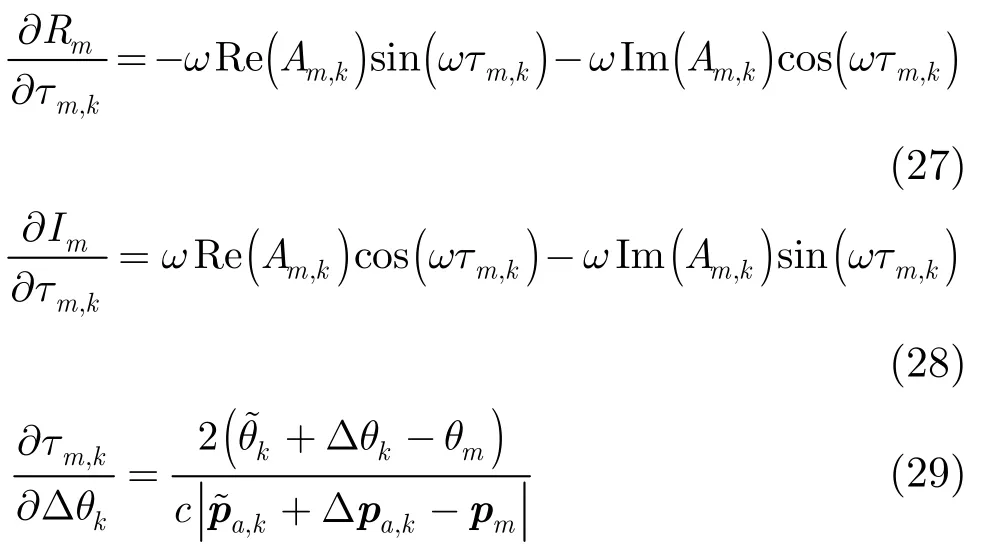
为了简化表达形式，令

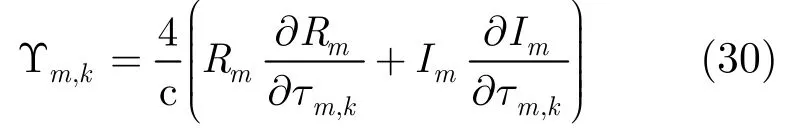
获得式（31）后，即可求得目标函数关于Δθk的偏导数，为：

（∂f）/（∂Δzk）中不含像素点的z坐标分量，这是因为我们选择地平面为成像空间，所有像素点的高度均为零。式（32）形式较复杂，通过进一步处理，将会看到一定规律，并以此将目标函数梯度形式进行简化。将（∂f）/（∂Δθk），θ=x，y，z 组合成如式（33）所示向量：

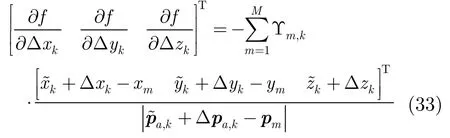
将式（34）代入式（33），得到

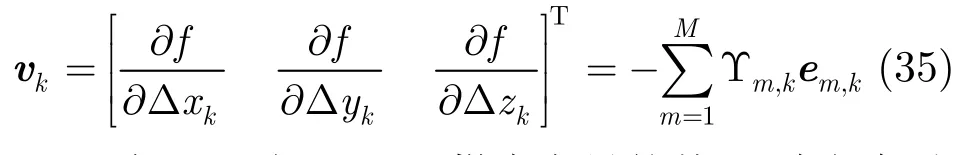
现在，vk为f（Δpa）梯度向量的某3个相邻分量，最后即可得到目标函数f（Δpa）的梯度为：

3.3算法步骤

对于共轭梯度法，另一个重要的步骤就是线性搜索。本文采用Armijo线搜索方法［17］，以保证目标函数在搜索方向上“充分下降”。

结合共轭梯度法原理，APC误差估计方法处理步骤如下：

（1）设置β和σ分别满足：0＜β＜1，0＜σ＜ 0.5，令j=0，

（3）令j=j+1，然后跳转到步骤2（2）。

步骤4计算

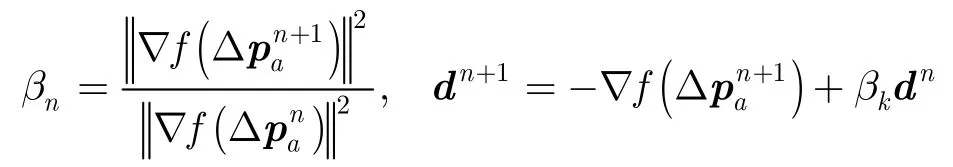
步骤5令n=n+1，然后跳转到步骤2。

从上面的算法原理和步骤可以看出，除了其他少量内存开销外，在迭代过程中仅仅只需要存储M个累加后向投影值，相比于ABP算法，内存需求降低了K倍。

另外，由于本文算法基于最优化技术，迭代求解将耗费大量时间，因此需要考虑如何提高算法效率。其中一种可行的方法是缩小图像空间搜索区域，为了获得良好的聚焦效果，该区域应该选择在强点周围，而强点位置可以通过利用测量到的APC进行粗聚焦BP成像后获得。但是，如果场景中没有强点，该方法将失效，仍然需要进行全图像空间搜索。在这种情况下，并行处理器件（如GPU［18］等）可以用来加速迭代算法和最后的精确聚焦BP成像。虽然迭代算法整体很难进行并行化，但在每次迭代中，计算目标函数梯度和图像强度却很容易做到并行实现。

4　实验结果及分析

本节将通过仿真，对比分析APC误差估计算法的性能，并通过实测数据处理结果进一步验证本文算法的有效性。

4.1仿真分析

仿真参数见表1所示。参考点目标（场景中心）位置为pc=［300000］Tm，两个非参考点目标的位置分别为pω1=［315000］Tm和pω2= ［30001500］Tm，其中pω1在距离向偏离参考点目标150 m，pω2在方位向偏离参考点目标150 m。为了模拟运动误差，APC高度向加上在［-10λ，10λ］之间均匀分布的随机误差。

表1　仿真参数Tab.1　Simulation parameters

利用直线APC处理的参考点目标成像结果如图3（a）所示，可见，点目标完全散焦，这是因为不精确的APC造成了相位补偿存在较大误差。为了降低运算量，仅选择局部像素点区域作自聚焦处理。从图3（a）可以看到，点目标能量虽然散开，但图中存在一个相对较强的像素点，以此像素点为中心，在其周围划定一个区域进行自聚焦处理，该区域包含该强像素点散开的大部分能量，这里我们仅选择9个像素点，如图3（b）所示。

以图3（b）中选择的像素点区域分别进行ABP处理和APC估计，ABP得到的相位误差用来补偿图像相位，而本文方法估计出的APC再次用来进行BP成像。采用这两种方法的参考点目标成像结果如图4所示。从图4中可以看出，虽然ABP对背景噪声抑制能力较强，且得到的图像强度高，但其距离向旁瓣升高，而本文方法成像性能良好。

图4中的结果为参考点目标的成像，两种方法的区别还不大明显，下面将给出非参考点目标pω1和pω2的成像结果。对于ABP算法，用参考点周围局部区域估计的相位误差去补偿非参考点周围场景的相位；对于本文方法，用估计的APC对非参考点周围场景进行成像。图5给出了仿真结果，其中，图5（a）和图5（b）为pω1的图像，可见，ABP算法无法处理运动误差空变的问题，当目标偏离参考点目标时，成像质量下降，主要影响包括距离向主瓣展宽和旁瓣升高，而本文方法克服了此问题；图5（c）和图5（d）为pω2的图像，对比图4（a）所示参考点目标图像可知，非参考点成像性能相似，几乎没有下降，这正好验证了第2节中关于运动误差空变性的分析，即运动误差在距离向的空变性比在方位向大很多。需要说明的是，图5（c）和图5（d）中方位向分辨率较低，这是因为方位向偏离的非参考点合成孔径不完整，造成方位向带宽减小，并不影响结论。

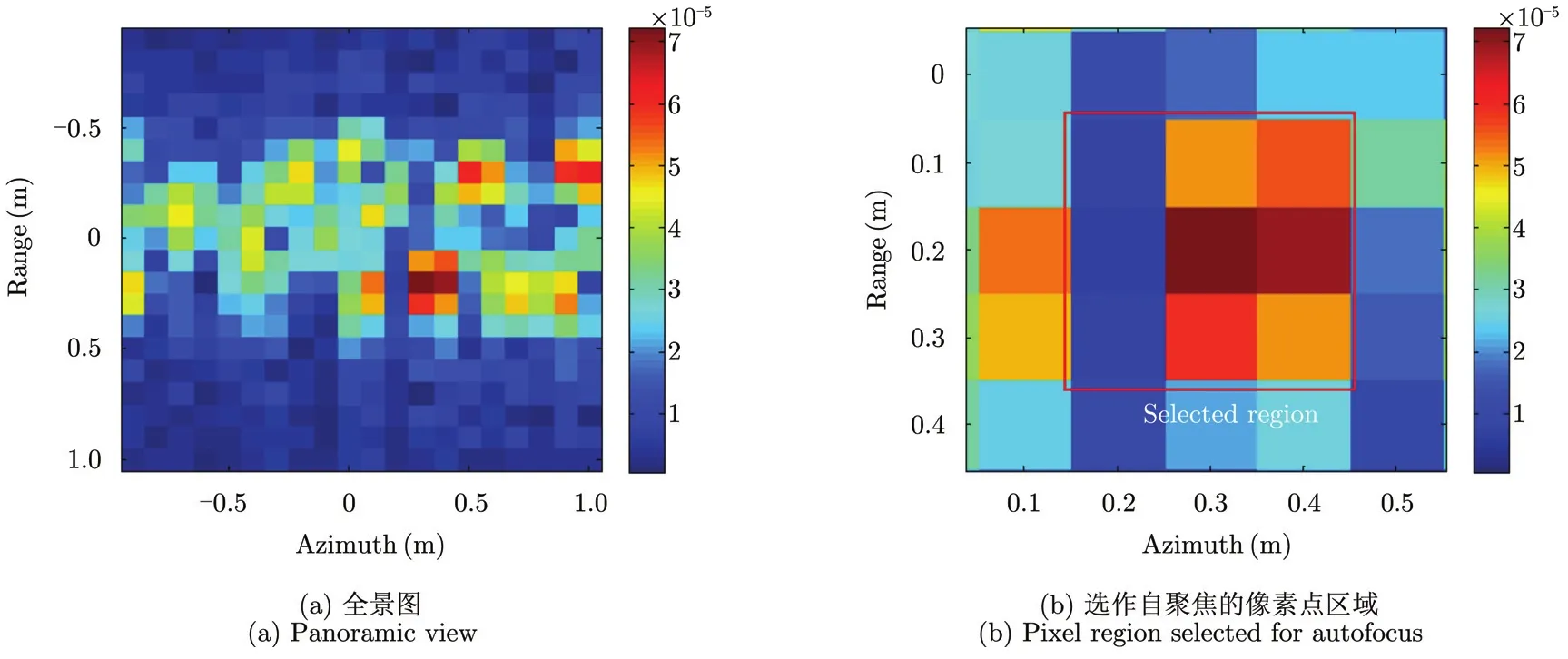
图3　参考点目标粗聚焦成像结果Fig.3　Coarse imaging results for reference target

为了分析估计APC的特点，将估计APC与真实APC在3个方向的对比曲线如图6所示。可以看出，在X方向和Y方向的估计误差极小，但在Z方向，估计APC与真实APC相差非常大。进一步分析可知，估计APC和直线APC与参考点目标的双程斜距差最大值约为0.01 m，该值小于λ=0.03 m，主要原因有两点：一是选作自聚焦的像素点并非真实的参考点目标位置；二是存在相位模糊，即APC误差导致的双程斜距误差大于λ时将出现相位反折，这样，双程斜距误差始终不会超过λ。可是，即便上述原因导致估计APC与真实APC在Z方向相差甚远，但目标聚焦性能仍然较好，这是最优化图像强度的结果，进一步验证了使用图像强度作为图像聚焦深度评价指标的合理性。

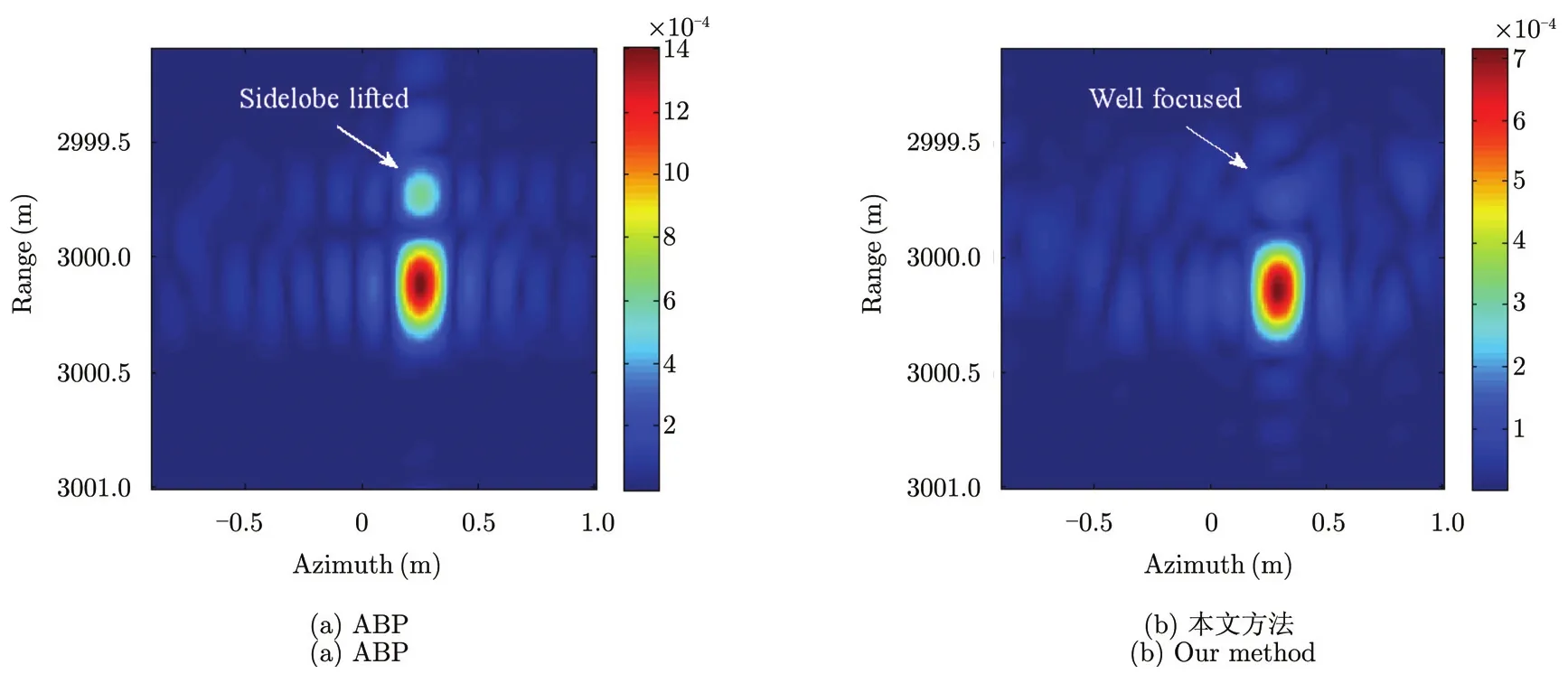
图4　参考点目标精聚焦成像结果Fig.4　Autofocus results for reference target

图5　非参考点目标精聚焦成像结果Fig.5　Autofocus results for non-reference target

4.2实测数据处理

本小节实测数据来源于某SAR系统，在该系统中，没有用IMU等运动传感器测量天线姿态误差，只用了GPS来测量雷达平台粗略的位置和速度，因此无法获得精确的天线相位中心。成像处理时，选取的APC数目为K=5000，2维图像空间像素点数为M=1000×1000，即距离向和方位向均为1000。首先，利用由GPS记录的平台初始位置和速度计算出的线性APC进行BP成像，结果如图7（a）所示。可以看出，由于直线APC精度远远不够，图像严重散焦，无法辨认场景目标。

从内存需求上看，仅考虑整个算法中占用大部分内存的迭代过程，ABP算法需要的内存空间至少为K×M×2×8≈74.5GB，远远超过了一般计算机的内存总量。此时，ABP算法已经无法适用。而APC误差估计算法中，对应部分内存需求仅为K×3×2×8≈234 kB 。下面采用APC误差估计方法进行运动补偿。为了提高处理效率，仅选取图7中一个强点目标周围的矩形区域来估计APC误差。最终成像结果如图7（b）所示。显然，整个图像空间聚焦效果比图7（a）大幅改善，可清晰地分辨出场景中的房屋和田埂。

为了分析估计APC的特点，将估计APC与线性APC的误差绘制于图8中，其中图8（a）为全景图，图8（b）为局部放大图。从图中可以看出，平台在Y方向（与方位向非常靠近）的抖动极小，可以忽略，平台在X方向的抖动最大，从图8（b）还可以看出，APC误差存在周期性变化，但值得注意的是，这种周期性变化的规律并非真实平台抖动的规律，而是由于相位模糊造成的，这种现象出现在估计出的平台抖动斜距误差大于一个波长时，此时相位超过2π，从图8（a）可以看出，APC误差在3个方向大部分均在一个波长（0.03 m）以下，X方向其他超出一个波长的部分，是其他两个方向综合作用的结果，图8（a）中的这一现象证实了相位模糊是导致APC误差周期变化的原因。为了解决这一问题，可以在APC估计模型中加入约束，使APC在3个方向的轨迹满足连续性条件，这将在后续工作中深入展开。

图6　估计APC与真实APC对比Fig.6　Comparison of estimated APC and actual APC

图7　实测数据处理结果Fig.7　Real data processing results

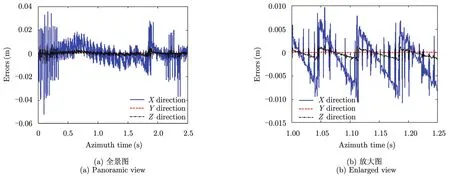
图8　估计APC与直线APC误差Fig.8　Error between estimated APC and linear APC

5　结论

本文针对ABP算法忽略运动误差空变性问题，提出了一种适用于BP算法的高精度运动补偿方法，该方法基于图像强度最优准则，利用最优化技术估计天线相位中心误差。与ABP算法相比，本文方法一方面极大提高了整个场景的相位补偿精度，另一方面大幅降低了内存需求，对大场景、长孔径、高分辨和高精度SAR成像具有重要意义。

［1］Sherwin C W，Ruina J P，and Rawcliffe R D.Some early developments in synthetic aperture radar［J］.IRE Transactions on Military Electronics，1962，MIL-6（2）:111-115.

［2］Weib M，Ender H G，and Gierull C H.Foreword to the special issue on scientific and technological progress of synthetic aperture radar（SAR）［J］.IEEE Transactions on Geoscience and Remote Sensing，2013，51（8）:4363-4365.

［3］M J J，Wit De，Meta A，et al..Modified range-Doppler processing for FM-CW synthetic aperture radar［J］.IEEE Geoscience and Remote Sensing Letters，2006，3（1）:83-87.

［4］Li Zhong-yu，Wu Jun-jie，Li Wen-chao，et al..One-stationary bistatic side-looking SAR imaging algorithm based on extended Keystone transforms and nonlinear chirp scaling［J］.IEEE Geoscience and Remote Sensing Letters，2013，10（2）:211-215.

［5］Li Zhong-yu，Wu Jun-jie，Yi Qing-ying，et al..An Omega-k imaging algorithm or translational variant bistatic SAR based on linearization theory［J］.IEEE Geoscience and Remote Sensing Letters，2014，11（3）:627-631.

［6］Peters T M.Algorithm for fast back- and re-projection in computed tomography［J］.IEEE Transactions on Nulear Science，1981，28（4）:3641-3647.

［7］Shi J，Ma L，and Zhang X L.Streaming BP for non-linear motion compensation SAR imaging based on GPU［J］.IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2013，6（4）:2035-2050.

［8］Fan Bang-kui，Ding Ze-gang，Gao Wen-bin，et al..An improved motion compensation method for high resolution UAV SAR imaging［J］.Science China Information Sciences，2014，57:122301-13.

［9］Ouyang Y，Chong J S，Wu Y R，et al..Simulation studies of internal waves in SAR images under different SAR and wind field conditions［J］.IEEE Transactions on Geoscience and Remote Sensing，2011，49（5）:1734-1743.

［10］Ding Z G，Liu L S，Zeng T，et al..Improved motion compensation approach for squint airborne SAR［J］.IEEE Transactions on Geoscience and Remote Sensing，2013，51（8）:4378-4387.

［11］Kennedy T A.Strapdown inertial measurement units for motion compensation for synthetic aperture radars［J］.IEEE Aerospace and Electronic Systems Magazine，1988，3（10）:32-35.

［12］Chen Tsung-lin.Design and analysis of a fault-tolerant coplanar gyro-free inertial measurement unit［J］.Journal of Microelectromechanical Systems，2008，17（1）:201-212.

［13］Li Jian-li，Fang Jian-cheng，and Ge Sam Shu-zhi.Kinetics and design of a mechanically dithered ring laser gyroscope position and orientation system［J］.IEEE Transactions on Instrumentation and Measurement，2013，62（1）:210-220.

［14］Kang C W，Cho N I，and Park C G.Approach to direct coning/sculling error compensation based on the sinusoidal modelling of IMU signal［J］.IET Radar，Sonar & Navigation，2013，7（5）:527-534.

［15］Ash J N.An autofocus method for backprjection imagery in synthetic aperture radar［J］.IET Geoscience and Remote Sensing Letters，2012，9（1）:104-108.

［16］Kayanthara K，Rao S，and Sarkar T.Analysis of twodimensional conducting an dielectric bodies utilizing the conjugate gradient method［J］.IEEE Transactions on Antennas and Propagation，1987，35（4）:451-453.

［17］Larry A.Minimization of functions having Lipschitz continuous first partial derivatives［J］.Pacific Journal of Mathematics，1966，16（1）:1-3.

［18］Owens J D，Houston M，Luebke D，et al..GPU computing［J］.Proceedings of the IEEE，2008，96（5）:879-899.

胡克彬（1988-），男，四川人，目前为电子科技大学工学博士研究生，主要从事高精度SAR成像技术研究。

E-mail:kbhu_work@126.com

张晓玲（1964-），女，四川人，获电子科技大学工学博士学位，目前为电子科技大学教授/博士生导师，主要从事SAR成像技术、雷达探测技术研究。

E-mail:xlzhang@uestc.edu.cn

师君（1979-），男，河南人，获电子科技大学工学博士学位，目前为电子科技大学副教授，主要从事SAR 数据处理方面研究。

E-mail:shijun@uestc.edu.cn

韦顺军（1983-），男，广西人，获电子科技大学工学博士学位，目前为电子科技大学讲师，主要从事 SAR 成像技术、干涉 SAR 技术研究。

E-mail:weishunjun@uestc.edu.cn

A High-precision Motion Compensation Method for SAR Based on Image Intensity Optimization

Hu Ke-binZhang Xiao-lingShi JunWei Shun-jun
（School of Electronic Engineering，University of Electronic Science and Technology of China，Chengdu 611731，China）

Owing to the platform instability and precision limitations of motion sensors，motion errors negatively affect the quality of synthetic aperture radar（SAR）images.The autofocus Back Projection（BP）algorithm based on the optimization of image sharpness compensates for motion errors through phase error estimation.This method can attain relatively good performance，while assuming the same phase error for all pixels，i.e.，it ignores the spatial variance of motion errors.To overcome this drawback，a high-precision motion error compensation method is presented in this study.In the proposed method，the Antenna Phase Centers（APC）are estimated via optimization using the criterion of maximum image intensity.Then，the estimated APCs are applied for BP imaging.Because the APC estimation equals the range history estimation for each pixel，high-precision phase compensation for every pixel can be achieved.Point-target simulations and processing of experimental data validate the effectiveness of the proposed method.

Synthetic Aperture Radar（SAR）； High-precision motion compensation； Autofocus back projection；Spatial variance

TN958

A

2095-283X（2015）01-0060-10

10.12000/JR15007

胡克彬，张晓玲，师君，等.基于图像强度最优的SAR高精度运动补偿方法［J］.雷达学报，2015，4（1）:60-69.http://dx.doi.org/10.12000/JR15007.

Reference format:Hu Ke-bin，Zhang Xiao-ling，Shi Jun，et al..A high-precision motion compensation method for SAR based on image intensity optimization［J］.Journal of Radars，2015，4（1）:60-69.http://dx.doi.org/10.12000/ JR15007.

2015-01-16收到，2015-03-05改回

国家自然科学基金（61101170），博士点基金（20110185110001）和航空科学基金（20142080007）资助课题

胡克彬kbhu_work@126.com