基于曲面投影的毫米波InSAR数据成像方法

韦顺军　师　君　张晓玲　陈　刚

①（电子科技大学电子工程学院　成都　611731）②（西安测绘研究所　西安　710054）

基于曲面投影的毫米波InSAR数据成像方法

韦顺军*①师君①张晓玲①陈刚②

①（电子科技大学电子工程学院成都611731）
②（西安测绘研究所西安710054）

与其它波段相比，毫米波系统具有体积小、重量轻、分辨率高等优点，成为近几年InSAR技术的研究热点。但因其波长短，毫米波InSAR对平台运动轨迹测量精度要求更高，非理想运动情况下传统成像方法数据处理及干涉相位提取困难，另外传统方法基于平面投影成像，在地形陡变时干涉相位缠绕和目标几何畸变较严重。为了解决传统方法在毫米波InSAR成像的以上不足，该文提出了一种基于曲面投影的毫米波InSAR成像方法，将不同通道回波数据投影到相同地形高程曲面上进行成像及干涉相位提取，并推导了曲面下地形高程与干涉相位的关系。仿真和实测数据结果验证了该文方法的有效性，结果显示该方法在平台非理想运动下较传统算法获得更好的InSAR成像和干涉相位质量，且减小了地形高程起伏引起的几何畸变及干涉相位缠绕，更有利于毫米波InSAR图像地形特征描述及高程提取。

干涉SAR（InSAR）；毫米波；曲面投影；干涉相位；高度反演

1　引言

由于波长较短，毫米波对地面目标穿透能力远小于厘米波，特别适合于提取观测对象的表面信息，有利于形成观测对象的高精度数字表面模型，故与分米波、厘米波相比，在相同干涉基线长度下毫米波InSAR更易于实现超高分辨率成像及高精度高程测量，且毫米波系统因其体积小重量轻，在小型及有限负荷平台上（如无人机等）更具优势。因此，毫米波InSAR技术及其应用已成为近年SAR技术的研究热点，国内外也纷纷开展了毫米波InSAR系统研制［1－10］。目前国外机载毫米波InSAR系统研究主要有美国Sandia实验室和德国FGAN研究所。美国Sandia 实验室从1996 年起已相继研发多款高精度机载干涉毫米波SAR成像系统，如Twin-Otter干涉SAR系统，其工作在Ka，Ku等波段，高程精度已经达到0.5 m［7］。2004年以来，德国FGAN FHR利用研制的高分辨毫米波SAR系统（MEMPHIS系统，该系统同时工作在35 GHz 和94 GHz），采用多基线实现干涉测量，提供的高程精度可达到0.2 m［9，10］。在国内，2011年中国科学院电子学研究所成功验证了我国第1部机载毫米波三基线InSAR原理样机，在3 km航行高度上实现了地面成像分辨率优于0.5 m及高程测量精度优于1 m的成像结果［1，5］。可以预见，随着雷达硬件水平和毫米波SAR技术的不断提高，不远的将来，会有更多的毫米波InSAR系统会投入到实际应用中。

目前，毫米波InSAR成像主要采用经典频域成像算法，如RD，CS和ωK算法等［8］，在各个天线对应的斜距平面（也称为方位-距离平面）上投影成像。虽然频域成像算法运算效率高，但均基于SAR多普勒质心及多普勒斜率模型，当平台运动轨迹较为复杂时在毫米波InSAR成像会有以下不足：（1）基于场景参考点函数进行成像，在场景非参考点成像时存在函数失配，容易引起成像散焦及相位误差；（2）因风场、湍流等因素影响，平台运动轨迹较理想轨迹可能存在较大的偏差，此时成像处理复杂，运动误差难以精确估计与校正，容易导致干涉相位提取精度降低；（3）数据投影于各天线独自的斜距平面成像，起伏地形的顶底倒置、掩叠等畸变严重，几何校正困难。与频域成像算法相比，后向投影（BP）算法采用逐点匹配及相干积累的处理方法，易于并行化处理，可实现运动测量数据（IMUGPS等）与成像处理的充分结合，尤其适合于复杂运动情况下毫米波SAR成像处理［11］。文献［12］提出了基于BP处理的InSAR成像方法，该方法结合IMU GPS等轨迹精确测量数据，在InSAR平台运动轨迹跳动情况仍然可以良好实现InSAR聚焦成像和相位提取。文献［7］分析了时变基线对机载 InSAR数据处理的影响，提出了基于BP算法的时变基线InSAR数据处理方法。与RD和CS等频域算法相比，BP算法处理过程不存在目标和雷达的斜距近似误差，在非理想运动条件下可提高干涉相位提取精度。然而，目前BP算法是将InSAR回波数据投影到平面空间（斜距平面或地平面等）进行成像处理，故其相位分布仍然与传统频域算法相似，在地形起伏剧烈时干涉相位条纹过密，不利于后期干涉相位解缠。另外，由于毫米波SAR分辨率高、采样单元小，相同地形起伏引起的几何畸变在毫米波SAR图像中对应的分辨单元更多，不利于后期几何畸变校正和目标特征提取。

为了克服传统平面投影算法在毫米波InSAR起伏地形成像带来的相位条纹过密、几何畸变等问题，本文提出了一种基于曲面投影的毫米波InSAR成像方法，将毫米波SAR主副数据投影到相同的地形曲面空间进行成像，推导了曲面投影时地形相对高程与干涉相位的数学关系，然后在未知地形高程情况下利用迭代处理方法，将InSAR数据投影到估计的高程曲面以逐次逼近真实的地形高程，最终可在毫米波InSAR数据成像中同时实现地形高度反演。文章主要结构如下：第2节简单介绍了InSAR成像模型，阐述了传统平面成像投影算法存在的问题；第3节推导了曲面下干涉相位与地形高度的关系，然后给出了曲面投影成像方法的基本步骤；第4节结合毫米波InSAR仿真以及实测数据，分析曲面投影成像算法的性能，验证了算法的有效性；第5节给出了本文算法的主要结论。

2　InSAR成像原理

2.1InSAR成像模型

InSAR成像的典型几何模型如图1所示。假设InSAR主副天线采用单发单收模式，场景中某个散射点位置为Pw=［x，y，z］T，散射系数为σ（Pw），基线长度为B，由基线分开的两条直线为主副天线真实的运动轨迹，虚线为主副天线理想的运动轨迹，PM（n）和PS（n）分别为主副天线在第n个方位时刻的位置，其到点目标Pw的斜距分别记为其中表示向量2范数运算符。

假设2维成像聚焦后散射点Pw的主副天线信号近似为：

图1　InSAR观测几何模型Fig.1　The geographic model of InSAR measurement

其中γM-ar（Pw），γS-ar（Pw）分别为目标Pw对应的InSAR主副天线方位-距离模糊函数，φM（Pw）和φS（Pw）分别为目标Pw在主副天线图像对应的相位。此时，散射点Pw的干涉相位可表示为：

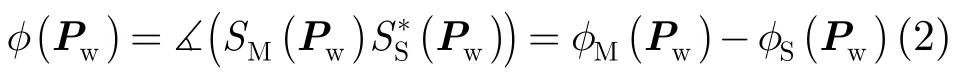
目前，InSAR成像主要采用经典频域成像算法，如RD，CS和ωK算法等，将InSAR主副天线的回波数据投影到各天线对应的斜距平面上投影成像，然后利用主副天线与目标的三角几何关系和干涉相位反演出地形高程。基于经典频域成像算法的InSAR地形反演基本步骤包括：数据成像、干涉相位提取、滤波、相位解缠、高程估计和校正等［13］。但是如前文所述，频域成像算法在高精度毫米波InSAR成像时仍然存在诸多问题亟待解决。

2.2平面投影成像

BP算法是一种基于时域相干处理的成像算法，其基本思想是利用投影成像区域内分辨单元到SAR天线平台之间的时延，将对应SAR回波信号进行相干累加，从而实现每个分辨单元聚焦成像。与RD和CS等频域算法相比，BP算法处理过程不存在近似误差，非常适用于任意运动轨迹及任意工作模式（大斜视、聚束式、双基等）SAR成像处理，已被成功用于复杂运动轨迹情况下的高精度InSAR成像处理［6，12］。BP成像算法主要步骤如下：

步骤1确定投影成像的平面空间，划分投影平面空间单元格；

步骤2回波数据距离压缩与插值，处理后数据记为Sr（r，n）；

步骤6遍历所有平面投影空间单元格和方位向慢时刻进行上述操作，即可完成BP成像处理。

图2为InSAR成像投影空间。虽然BP算法可以自由选择成像投影空间，但是在目前InSAR成像处理中，BP算法仍然与传统频域成像算法相似，将回波数据投影到某一个平面（斜距平面或水平地面）上进行成像。对于平面投影的成像处理，若地形高程陡变时，InSAR图像中干涉相位条纹往往过于密集甚至断裂，不利于后期的相位解缠，容易增大高程反演误差。另外，起伏地形在平面上投影时也会造成几何畸变，尤其在毫米波InSAR，因其波长短成像精度高、分辨单元小，地形高程起伏引起的几何畸变将对应于SAR图像中更多的分辨单元，非常不利于后期几何校正和目标特征提取。因此，如何克服现有平面投影算法在毫米波InSAR在起伏地形成像面临的干涉相位过密、图像几何畸变等缺陷，需结合InSAR成像原理进行新方法研究。

图2　InSAR成像投影空间Fig.2　The imaging projection space of InSAR

3　曲面投影InSAR成像

3.1干涉相位提取原理

为了克服目前平面投影成像算法的不足，本文将毫米波InSAR主副天线的回波数据投影到相同的地形高程曲面进行成像处理，提出了一种基于曲面投影的BP成像算法，简称曲面BP算法。

根据SAR成像信号模型，距离压缩后点目标Pw的主副天线回波信号可表示为：

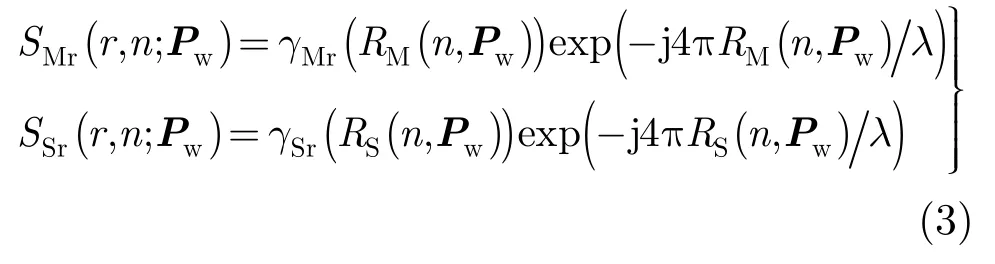
其中，γMr（RM（n，Pw））和γSr（RS（n，Pw））分别为Pw在主副天线中得到的距离模糊函数。

假设点目标Pw在地形曲面空间的投影点为，曲面BP算法对式（3）中InSAR主副天线数据，同时补偿主天线多普勒相位函数及投影点到各天线参考斜距信息，得到

其中，n0为方位向上的参考慢时刻，SMr（n，Pw）和SSr（n，Pw）分别为Pw在主副天线中对应的距离压缩后回波数据，R（n，）和R（n，）分别表示投MS影点在第n个方位时刻到InSAR主副天线的斜距。

根据式（3）和式（4），假设目标散射系数在主副天线中完全相同，在远场条件下满足曲面BP算法中点目标的干涉相位φ）为：T2

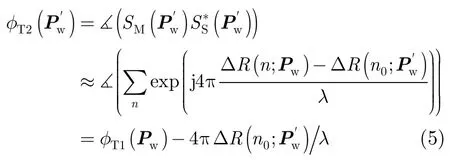
对于远场条件SAR成像，合成孔径长度通常远小于平台天线到场景的斜距，即La≪R（n，Pw）。对于合成孔径时间内的任意方位向时刻n，则有

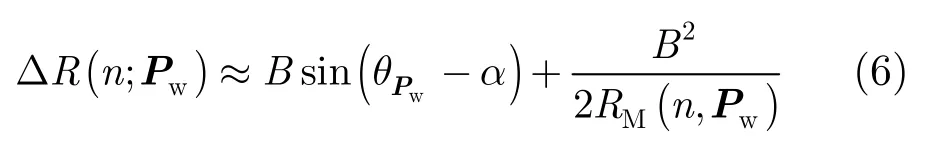
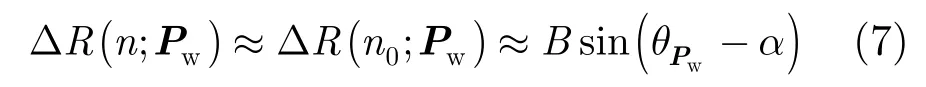
因此，场景点目标Pw对应的斜距差相位φT1（Pw）可表示为：

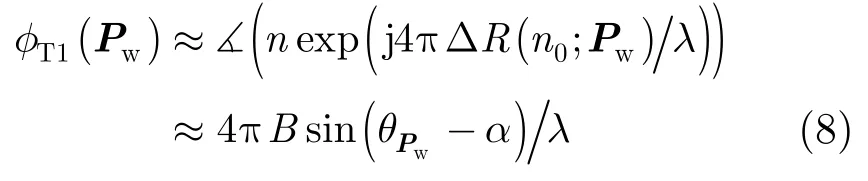
根据式（7），得到

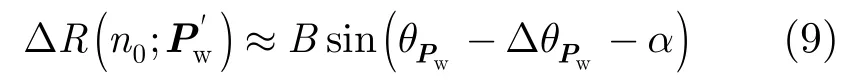
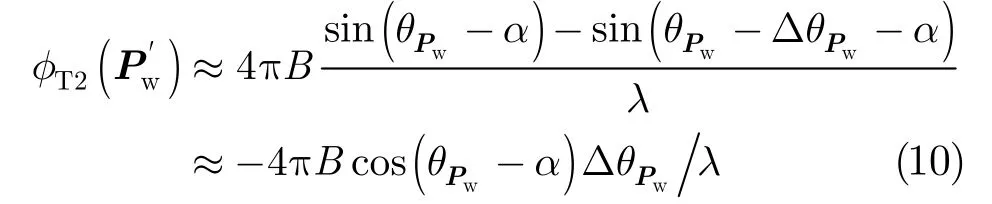
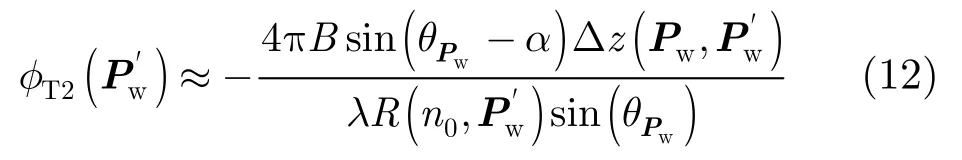
由于实际中未知地形的真实高程信息，本文曲面BP采用迭代处理思想，先选择水平地面作为投影曲面初值，根据该投影获取干涉相位并反演高程，反演得到的地形高程再作为下一次迭代的投影曲面，利用多次迭代从而可以逐步减少干涉相位缠绕，并且估计得到的地形高程越逼近真实的地形高程。

3.2算法流程

根据3.1节干涉相位提取原理，基于迭代处理的曲面BP算法的主要步骤如下：

步骤1InSAR回波数据距离压缩与插值，处理后数据记为SMr（n，Pw）和SSr（n，Pw）；

步骤2给出初始地形高程曲面Ω（0）、迭代最大次数M0、迭代条件阈值η0，迭代次数i=0；

步骤3在第i次迭代过程中，均匀划分地形高程曲面Ω（i），对于曲面中每一个单元格，计算其距离历史

步骤4根据式（4），采用BP算法得到第i次迭代过程中的主副天线图像，记为和

步骤6根据式（12）计算得到相对地形高程Z，并且更新第i+1次迭代的地形高程曲面Ω（i +1）=Ω（i ）+Z；

从迭代曲面BP算法步骤可知，估计得到的第i次迭代地形高程（i）Ω越来越接近真实地形高程，而相对地形高程Z则随着迭代次数增加越来越小。一般情况下，迭代次数为10多次时即可满足估计精度要求。本文中选择相对地形高程Z作为迭代终止条件，另外也可以选择残余干涉相位或者相邻迭代间估计结果的变化量作为迭代终止条件。从曲面BP算法原理可知，该算法不仅保持传统BP算法的成像性能，可对复杂运动条件下InSAR数据进行良好聚焦，还保留主副天线到场景目标的斜距差相位，得到曲面投影点目标的干涉相位能够实现曲面空间高精度成像和干涉相位提取。

4　数据成像结果

4.1仿真数据结果

为了验证曲面投影算法在毫米波InSAR的成像性能，本节利用面目标仿真数据进行分析。仿真主要参数为：雷达载频fc=37.5GHz ，发射信号带宽Br=1 GHz ，天线方位真实孔径长度D=0.3m ，平台高度H=3000 m，信号脉冲宽度Tr=5ms ，脉冲重复频率PRF=550Hz ，雷达入射角θ=45°，垂直基线长度平台做直线运动且速度服从均值为v=60m/s ，标准方差为σ=1m/s 的随机分布。仿真场景为圆锥曲面，圆锥场景大小为60 m×60 m ，锥心高度为16m，其场景如图3（a）所示，散射系数如图3（b）所示。在仿真过程中加入信噪比为25 dB的乘性随机噪声。

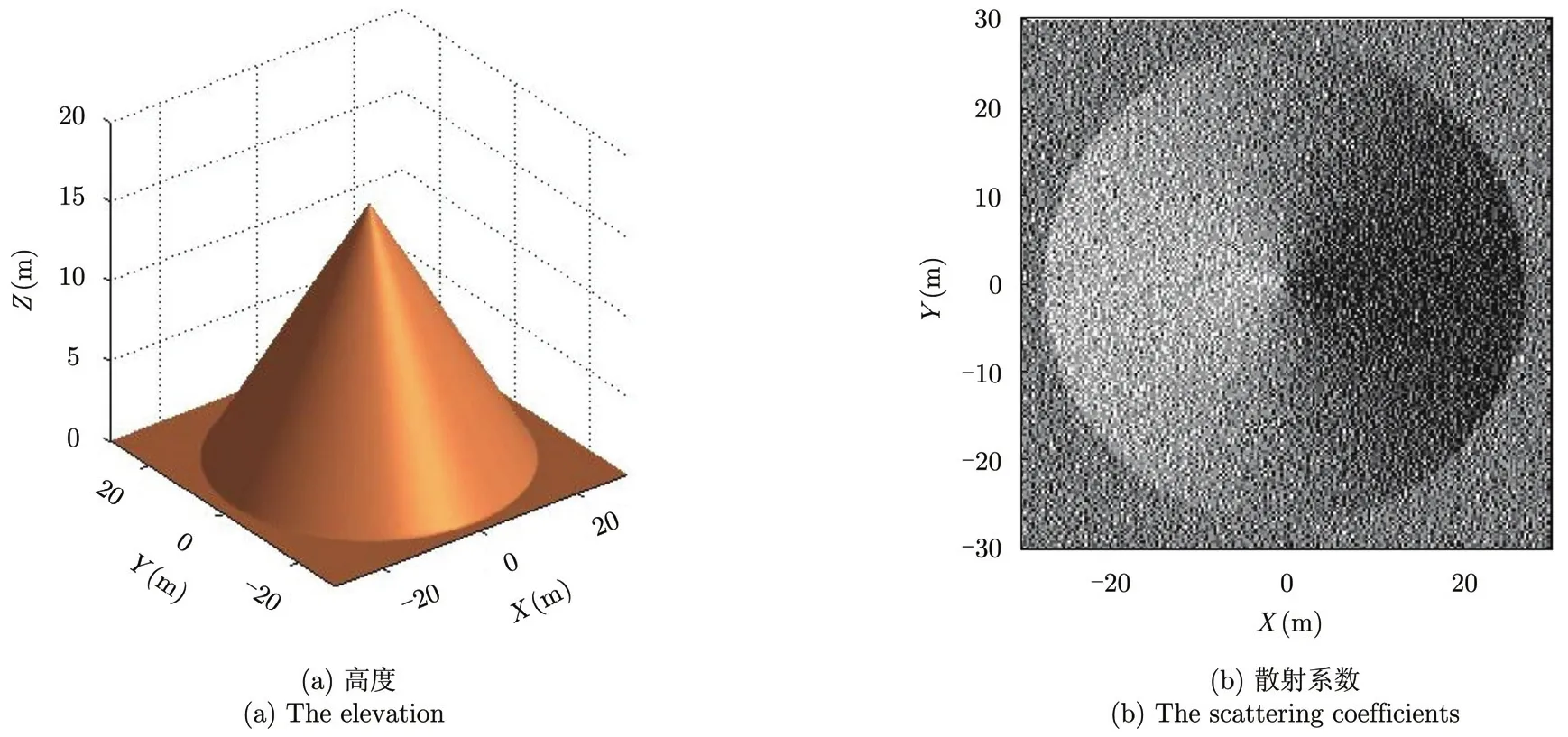
图3　原始仿真圆锥场景Fig.3　The original simulated cone

利用RD算法、地平面投影BP算法和本文曲面投影算法对主副天线圆锥场景仿真数据进行成像，得到的幅度图像和干涉相位如图4（b）-图4（d）所示，其中曲面投影算法中以真实圆锥高度作为投影曲面。从图4（a）-图4（c）可看出，因RD算法在斜距平面上成像，图像中圆锥底部在距离向的直径较真实值减小，圆锥高度导致圆锥中心左移，即同时存在水平和高度引起的几何畸变；地平面BP算法图像中圆锥底部直径和真实值基本相同，消除了水平引起的畸变，但圆锥高度同样导致了圆锥中心左移，即存在高度引起的几何畸变；曲面投影算法图像中圆锥几何形状与真实场景吻合，消除了水平和高度引起的畸变，更真实地描述了圆锥特征。从图4（d）-图4（f）可看出，RD算法中存在平地相位和高度相位混叠且干涉相位存在缠绕条纹，不利于目标高程反演；地平面投影BP算法中虽然去除了平地相位，但仍存在缠绕条纹，若条纹过密则相位解缠困难，同样不利于目标高程反演；曲面投影算法中相位不存在缠绕条纹，更有利于目标高度反演。

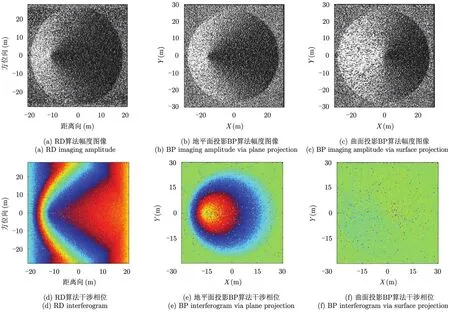
图4　仿真圆锥幅度图像及干涉相位Fig.4　The amplitudes and the interferograms of the simulated cone

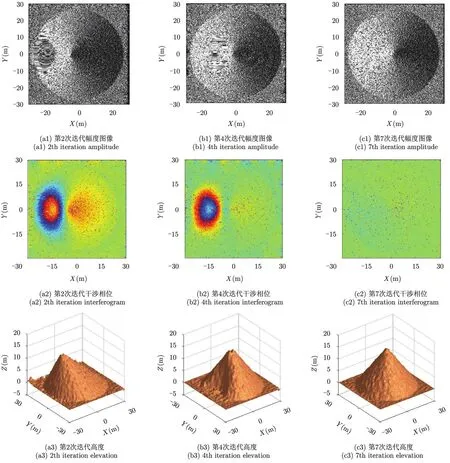
图5　迭代曲面BP仿真圆锥成像结果Fig.5　The imaging results of the simulated cone

表1　不同迭代次数的曲面BP算法估计高度和干涉相位评估Tab.1　Estimated elevation and interferometric phase of BP algorithm for different iteration times

4.2实测数据结果

为了进一步验证本文算法的有效性，本节利用某机载Ka波段毫米波InSAR实测数据进行成像分析，该InSAR系统采用天线一发双收的成像模式，基线长度为B=0.31m 。因为大气湍流等导致的机载平台抖动以及平台运动控制系统精度等非理想因素的影响，毫米波机载InSAR平台不能完成理想的匀速直线运动，而是做非直线非匀速运动，其主副天线的真实运动轨迹如图6（a）所示，运动轨迹在水面和高度向上有一定的弯曲。本文选取该系统获取的一段某城市郊区区域的观测数据进行成像，该观测数据的场景光学图如图6（b）所示，观测场景中地势比较平坦，场景中主要由农作物、树林、农田、小路和沟渠等组成。

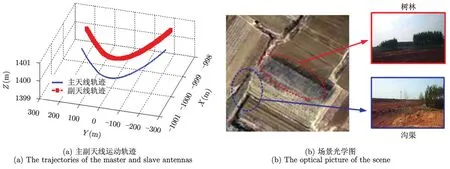
图6　毫米波InSAR天线轨迹与实验场景Fig.6　The trajectory of the millimeter-wave InSAR antennas and its underlying scene

图7　毫米波机载InSAR实测数据成像结果Fig.7　The results of millimeter-wave airborne InSAR real data

图7为分别用RD算法、地平面投影BP算法和曲面投影BP算法对实验场景毫米波InSAR数据进行成像得到的结果，其中，所有算法成像后的图像均进行了窗口为3×3的多视处理，图7（a）为主天线利用运动补偿后RD算法成像得到的幅度图，图7（b）为主天线利用地平面投影BP算法成像得到的幅度图，图7（c）为主天线利用曲面投影BP算法成像得到的幅度图，图7（d）为运动补偿后RD算法成像得到的干涉相位图，图7（e）为地平面BP算法成像得到的干涉相位图，图7（f）为曲面BP算法成像得到的干涉相位图。实测数据成像中RD成像算法采用基于子孔径处理的相位梯度自聚焦（PGA）方法进行运动补偿［14］，两种BP成像算法则利用真实的机载平台非直线轨迹进行成像，而且曲面投影BP算法采用了2次迭代处理。对比观测场景幅度图像图，因运动补偿后仍然会残留一定的误差，故运动补偿后的RD算法在某些农田和小路区域仍有一定的散焦，地平面投影BP和曲面投影BP算法结果则良好地实现了田地和植被等全部场景的聚焦。因观测场景地势较平坦，地形起伏引起的几何畸变较小，故3种算法成像结果中目标几何形状变化不明显。从图7干涉相位可明显看出，RD算法因其在斜距平面上投影成像，故存在3个条纹的平地相位，其干涉相位图条纹较多，不利于后期干涉相位解缠和高程反演；地平面投影BP算法去除了平地相位，但还存在地形起伏和树林高度引起的干涉相位，导致了干涉相位图的缠绕；曲面BP算法进一步去除了地形起伏和树林高度引起的干涉相位，干涉相位无缠绕，更有利于后期干涉相位处理。为了进一步比较成像算法的性能，从图7 中幅度图像结果中选择两个子区域进行放大显示，其幅度图如图8所示，其中子区域1中目标为农作物，子区域2中目标为多条田埂。通过图8对比可发现，较运动补偿后的RD算法，基于真实运动轨迹成像的地面投影BP和曲面投影BP算法的聚焦质量有了大幅度的提升，农作物形状和田埂分布等都清晰可见。由图7和图8可知，本文曲面投影BP算法可以实现非直线非匀速运动轨迹下毫米波InSAR数据的良好聚焦，并且减少了干涉相位缠绕，实验结果验证了曲面投影BP算法在InSAR成像的有效性。

图8　毫米波机载InSAR实测数据成像结果Fig.8　The results of millimeter-wave airborne InSAR real data

5　结论

本文针对传统平面投影成像方法在毫米波InSAR数据成像中存在的干涉相位缠绕过密、几何畸变等不足，提出了一种曲面投影的毫米波InSAR成像方法。该方法将毫米波InSAR原始回波数据投影到估计得到的地形高程曲面上进行成像，从而得到该地形高程曲面下的干涉相位，再利用该干涉相位进行高程地形反演得到相对高度，然后对高程曲面进行高度补偿，通过多次迭代逼近成像，得到最终的毫米波InSAR成像结果和地形高程。本文提出的曲面投影方法具有以下优点：

（1）采用后向投影成像算法，在理论上具有理想的成像聚焦和保相精度，相对于RD等频域成像算法，BP算法没有对斜距进行近似估计，能够实现成像空间中每个采样点的精确聚焦和高保相成像，有利于高精度地形高程反演。

（2）通过多次迭代成像，克服了由于InSAR成像机理造成的地形几何畸变的缺点，同时使得到的地形高程不断逼近真实地形，大大提高了毫米波InSAR高程反演的精度。

致谢感谢航天科工二院23所提供研究所需的Ka波段干涉SAR数据。

［1］李道京.毫米波干涉合成孔径雷达［J］.高技术与产业化，2013（11）:40-43.Li Dao-jing.Millimeter-wave interferometric SAR［J］.High-Technology & Industrialization，2013（11）:40-43.

［2］D'Addio S and Ludwig M.Modelling and analysis of rain effect on Ka-band single pass InSAR performance［C］.IEEE International Geoscience and Remote Sensing Symposium，Cape Town，South Africa，2009，4:913-916.

［3］Schmitt M and Stilla U.Adaptive multilooking of airborne Ka-band multi-baseline InSAR data of urban areas［C］.IEEE International Geoscience and Remote Sensing Symposium，Munich，Germany，2012:7401-7404.

［4］Mokadem A，Thirion-Lefevre L，and Colin-Koeniguer E.Analysing urban areas in the frame of non-line of sight target detection.Electromagnetic modelling，validation and application to real data in Ka-band［C］.International Conference on Electromagnetics in Advanced Applications，Torino，Italy，2013:543-546.

［5］潘舟浩，刘波，李道京，等.毫米波三基线InSAR系统误差校正和信号分析［J］.电子与信息学报，2011，33（10）:2464-2470.

Pan Zhou-hao，Liu Bo，Li Dao-jing，et al..Millimeter wave three baseline InSAR system error correction and signal analysis［J］.Journal of Electronics & Information Technology，2011，33（10）:2464-2470.

［6］刘波，潘舟浩，李道京，等.基于毫米波InISAR 成像的运动目标探测与定位［J］.红外与毫米波学报，2012，31（3）:258-264.

Liu Bo，Pan Zhou-hao，Li Dao-jing，et al..Moving target detection and location based on millimeter-wave InISAR imaging［J］.Journal of Infrared and Millimeter Waves，2012，31（3）:258-264.

［7］潘舟浩，李道京，刘波，等.基于 BP 算法和时变基线的机载InSAR 数据处理方法研究［J］.电子与信息学报，2014，36（7）:1585-1591.

Pan Zhou-hao，Li Dao-jing，Liu Bo，et al..Processing of the airborne InSAR data based on the BP algorithm and the time-varying baseline［J］.Journalof Electronics & Information Technology，2014，36（7）:1585-1591.

［8］Walker B，Sander G，Thompson M，et al..A highresolution，four-band SAR testbed with real-time image formation［C］.IEEE International Geoscience and Remote Sensing Symposium，Lincoln，NE，USA，1996，3:1881-1885.

［9］Magnard C，Meier E，Ruegg M，etal..High resolution millimeter wave SAR interferometry［C］.IEEE International Geoscience and Remote Sensing Symposium，Barcelona，Spain，2007:5061-5064.

［10］Magnard C，Meier E，Small D，et al..Processing of MEMPHIS millimeter wave multi-baseline InSAR data［C］.IEEE International Geoscience and Remote Sensing Symposium，Honolulu，HI，USA，2010:4302-4305.

［11］Shi Jun，Ma Long，and Zhang Xiao-ling.Streaming BP for non-linear motion compensation SAR imaging based on GPU［J］.IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2013，6（4）:2035-2050.

［12］师君，马龙，韦顺军，等.基于导航数据的Ka 波段InSAR 成像处理与分析［J］.雷达学报，2014，3（1）:19-27.Shi Jun，Ma Long，Wei Shun-jun，et al..Ka-band InSAR imaging and analysis based on IMU data［J］.Journal of Radars，2014，3（1）:19-27.

［13］王超，张红，刘智.星载合成孔径雷达干涉测量［M］.北京:科学出版社，2002:37-66.

Wang Chao，Zhang Hong，and Liu Zhi.Spaceborne Synthetic Aperture Radar Interferometry［M］.Beijing:Science Press，2002:37-66.

［14］Zhu Dai-yin，Jiang Rui，Mao Xin-hua，et al..Multisubaperture PGA for SAR autofocusing［J］.IEEE Transactions on Aerospace and Electronic Systems，2013，49（1）:468-488.

韦顺军（1983-），男，广西人，获电子科技大学工学博士学位，目前为电子科技大学讲师，主要从事 SAR 成像技术、干涉 SAR 技术研究。

E-mail:weishunjun@uestc.edu.cn

师 君（1979-），男，河南人，获电子科技大学工学博士学位，目前为电子科技大学副教授，主要从事SAR 数据处理方面研究。

E-mail:shijun@uestc.edu.cn

张晓玲（1964-），女，四川人，获电子科技大学工学博士学位，目前为电子科技大学教授/博士生导师，主要从事SAR成像技术、雷达探测技术研究。

E-mail:xlzhang@uestc.edu.cn

陈刚（1976-），男，陕西人，获国防科技大学工学硕士学位，目前为西安测绘研究所副研究员/副主任，主要从事InSAR 数据处理、干涉定标技术研究。

E-mail:splitter@263.net

Millimeter-wave Interferometric Synthetic Aperture Radar Data Imaging Based on Terrain Surface Projection

Wei Shun-jun①Shi Jun①Zhang Xiao-ling①Chen Gang②
①（School of Electronic Engineering，University of Electronic Science and Technology of China，Chengdu 611731，China）
②（Xi'an Research Institute of Surveying and Mapping，Xi'an 710054，China）

Millimeter-wave Interferometric Synthetic Aperture Radar（InSAR）has smaller size，lower weight，and higher resolution compared with other bands.Thus，it has become a hot research topic.However，owing to its shorter wavelength，millimeter-wave InSAR data processing requires high-precision measurements of platform motion.For nonideal trajectories，traditional methods face difficulties in echo imaging and interferogram extraction.In addition，existing methods mainly produce SAR images based on plane projection.When the terrain changes abruptly，these methods may cause strong interferometric phase unwrapping and geometric distortion in SAR images.To overcome the abovementioned disadvantages of conventional methods in millimeter-wave InSAR imaging，an approach based on terrain surface projection is proposed.The echoes of different antennas are projected on the same terrain surface space for data imaging and interferogram extraction.In addition，the relation between terrain elevation and interferometric phase is derived.Simulations and experimental results verify the effectiveness of the proposed method； furthermore，the proposed approach improves the precision of interferometric phase extraction in complex motion conditions，while minimizing geometric distortion and phase wrapping in rough terrain，which is more conducive to terrain description and elevation inversion.

InSAR； Millimeter-wave； Surface projection； Interferometric phase； Elevation inversion

TN957.52

A

2095-283X（2015）01-0049-11

10.12000/JR14137

韦顺军，师君，张晓玲，等.基于曲面投影的毫米波InSAR数据成像方法［J］.雷达学报，2015，4（1）:49-59.http://dx.doi.org/10.12000/JR14137.

Reference format:Wei Shun-jun，Shi Jun，Zhang Xiao-ling，et al..Millimeter-wave interferometric synthetic aperture radar data imaging based on terrain surface projection［J］.Journal of Radars，2015，4（1）:49-59.http://dx.doi.org/10.12000/JR14137.

2014-11-20收到，2015-02-05改回

国家自然科学基金（61101170），高分专项（GFZX0403060201）和高分专项青年创新基金（GFZX04060103-5-25）资助课题

韦顺军weishunjun@uestc.edu.cn