基于优化的复杂网络聚类方法综述*

曾 成，孙雅倩，徐玉珠，张达敏

(贵州大学大数据与信息工程学院，贵州 贵阳 550025)

0 引言

聚类方法的分析在诸多领域是非常重要的，在复杂网络研究方面也是相当关键的。分析中得到的数据簇(Cluster)称之为群(Group)或社团(Community)。研究指出，在复杂网络中，无论是大型还是小型的，簇内部不同节点之间一定有着关联。对复杂网络里面的聚类特点进行分析研究，就可以得到网络中节点与节点之间存在的某种关系［1－5］。

当前对于复杂网络聚类算法的研究已有很多不同算法。这些算法可以分为两种基本类别:首先是基于优化的方法(Optimization Method);再者就是启发式方法(Heuristic Method)［6－10］。其中基于优化是把优化这类问题运用到复杂网络聚类上。后者则把对预定义设计启发式规则这种方法在一定程度上应用于解决复杂网络聚类问题。对于基于优化的复杂聚类方法，细分为谱方法和局部搜索方法两种。本文主要介绍一些著名学者研究的比较经典的基于优化的复杂网络聚类方法，以及近年来一些新的改进算法及这类方法的实际应用。同时分析、总结了这些新型算法的优缺点，提出现有研究中存在的问题以及对未来的展望［10－14］。

1 经典的基于优化聚类方法

1.1 谱方法

谱方法是将二次型优化这个方法对被截的函数采用最小化预定义。被截的函数是指当一个网络一分为二时它所分成的两个子网间的连接程度的密度大小。当被分割出来的网络的被截函数最小时，则就可以判断这个分割是最优的网络分割。

1.1.1 基于Normal矩阵的谱平分法

基于经典的谱分析法，Capocci等人在2005年研究了一个新的算法，即基于Normal矩阵的社团发现算法［15］。算法中 Nmoral矩阵 N=K－1A，式中 K是一个对角矩阵，kii=aij对应不同节点的度，网络中节点的个数用n表示;A则为该网络的连接矩阵。可以知道，矩阵N是半正定矩阵，其实特征值有n个且最大为1。如要获得网络的簇结构则需要对各个不同特征向量里的元素进行对比。为此，可以设计一个连接参量来对社团的优良进行判别:

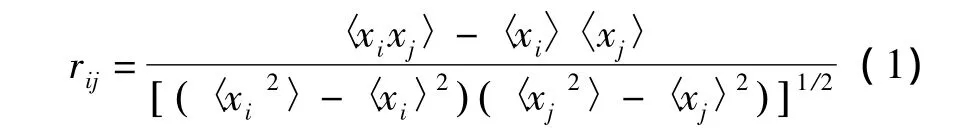
其中，〈.〉是对各个不同的特征向量里的元素取平均值，节点i和j的连接度用rij来判别。效果的好坏取决于特征向量的平均值。

1.2 局部搜索方法

Kernighan－Lin算法(简称KL算法)、快速Newman算法(简称FN算法)和Guimera－Amaral算法(简称GA算法)在基于局部搜索优化的方法是最具有代表性的算法。目标函数、候选解的搜索策略和最优解的搜索策略是此算法里的三个基本部分。

1.2.1 Kernighan －Lin 算法

Kernighan和Lin等人在70年代初提出了KL算法［16］，这个方法在图分割问题和复杂网络聚类上都得到了很好的运用。KL算法是对极小化社团间相连个数与社团内部相连个数之差进行优化;对于其候选解这一搜索策略具体为:将网络内不同社团之间的节点进行随机交换或者把节点进行转移，改变到另外的社团。从解的最初开始，KL算法在迭代过程中都会经历得到、判断、选择，停止的条件，从目前的解出发搜索到更优的候选解。KL算法在搜索时只选择更优的解，排斥所有较劣的解，所以它搜索到的解一般情况是局部最优解而非全局最优解。

1.2.2 快速Newman算法

2004年，Newman提出了快速复杂网络聚类算法FN［17］，此方法是基于局部搜索的。其目的是将Newman和Girvan提出的网络模块性评价函数也就是Q函数进行极大化的优化。Q函数的原始意义为社团内真实相连的个数与随机相连条件下社团内期望相连个数的差，此函数可以用来定量的表示出网络社团结构的好与坏，它的形式如下:

1.2.3 Guimera －Amaral算法

与FN算法优化目标相似的是，Guimera和Amaral在2005年提出了基于模拟退火算法(Simulated Annealing，SA)的复杂网络聚类算法GA，并把这一方法在一定程度上运用于新陈代谢网络研究中［18］。与KL算法相似的是，从解的最初开始，GA算法在迭代过程中都会经历得到、判断、选择，停止的条件是从当前解开始，一直搜索到找不到更优的候选解。GA算法计算出候选解的具体方法是:将网络内不同社团之间的节点进行随机交换或者把节点进行转移，改变到另外的社团，然后对网络社团合并或分解。GA采用的Metropolis准则定义如下:

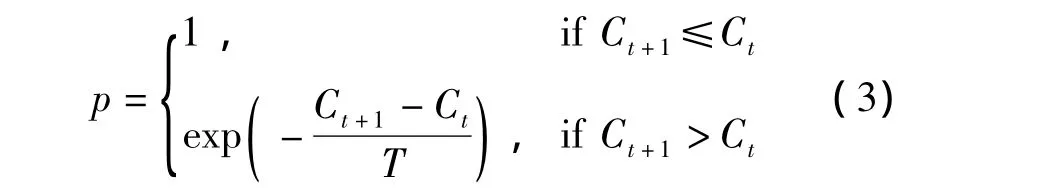
其中，Ct=－Qt，p表示接受t+1时刻选解的概率;T表示t+1时刻的系统温度。

1.2.4 GAS 算法

针对目前基于遗传算法(GA)的社团检测算法［19］大多存在寻优能力弱并且收敛慢的问题，2010年提出来一种改进的GAS算法［8］。基于“邻近的节点更加偏向聚在同一个簇里面”的现象，该算法在传统的基于0函数优化的GA算法框架中增加了“局部搜索算子”。GAS算法在优化Q函数过程中利用了节点的邻居节点信息，与传统算法相比，GAS算法搜索相对更快且更有效。

2 基于优化聚类方法的改进

2.1 基于PSO的复杂网络聚类算法

文献［20］基于谱方法的基本原理，设计出了基于PSO聚类的复杂网络社团结构算法。此算法的基本思想是将复杂网络聚类问题变成空间数据的聚类问题，为此首先可以运用的是谱方法里面的A－cut方法或N－cut方法;通过应用这两种方法将复杂网络里的社团结构信息变成由非平凡特征向量组成的空间数据集。原来复杂网络里的每一个节点被对应于这个空间数据集里面产生的每一个数据样本。复杂网络中节点的社团信息来自于对这个空间数据集里面的每一个数据样本进行聚类，然后由此可以完成对复杂网络的聚类。文献［20］把粒子群优化算法运用到复杂网络聚类里，PSO聚类算法有效结合了谱方法里面的平均截方法和规范截方法，进而产生了更加优异的复杂网络聚类算法。让谱方法的聚类精度与稳定性在复杂网络聚类里得到了大幅度提高。

2.2 FNCA 算法

目前对于Q函数的聚类算法的研究绝大多数都是在全局的基础上进行的，经典的聚类方法都是要设计一种高效的搜索策略来改良Q函数，将其进行优化。但是因为这些搜索策略在搜索过程中每进行一步都会用到全局的网络拓扑信息，所以它们的搜索效率一般情况下是相对低的。针对这一问题，不同与已有方法，文献［21］试图从局部观点出发，使网络中每个节点独立计算并优化自身的局部函数，并Q函数进行分析，此函数是面向全局网络的目标函数，由此可以推导出一个f函数(针对的是网络里面的每一个节点的目标函数)，此函数具有局部特征，并证明Q函数是跟着网络中每一个节点的f函数呈单调递增趋势的，最后导出一个基于f函数的快速网络聚类算法，即FNCA(Fast Network Clustering Algorithm)算法。

给定一个无向无权网络N(V，E)，假设点集V被划分(聚类)为若干个类簇。若网络中任一结点i的标签为r(i)，所属的类簇为cr(i)，Q则函数可定义为:

网络中所有节点的f函数之和用Q函数来表示。在其他节点标签不变的情况下，如果由于网络里面的任一节点标签的变化让其f函数值变大，那么这个变化就会直接引起Q函数值的变大。根据上述理论基础，提出了一个基于局部优化的快速网络聚类算法，即FNCA算法。

2.3 聚类算法FEC的改进

经典的FEC算法里面的发现簇(Finding Community，FC)算法对节点给出的随机游走步数参数值提出了一定的要求，实验最后的聚类结果受步数大小的影响。孔令旗［22］根据步数的经验值提出了一个区间，即［6，20］。其中区间开始的6代表复杂网络里面不同节点之间的平均路径长度(很大一部分网络都会受六度分离理论的影响);区间结束的20则代表网络的直径(研究表明万维网是目前最大的复杂网络，它的直径经测试为19)。分析认为把步数的区间设置为10到20就可以覆盖绝大部分网络聚类分析［23］。孔令旗等人提出了“簇内短回路丰富”这一启发式策略。因为社团内部的正连接相对紧密，且社团与社团之间的正连接比较疏散，同一社团内顶点节点，通过正连接组成三角形和四边形的概率要远大于不同社团间的概率。研究提出的“簇内短回路丰富”这一启发式策略结合顶点度极值，将会很好的帮助选择更“优”的目标节点。

2.4 基于连接强度的复杂网络聚类算法

丁转莲于2014年研究出了基于连接强度的种群初始化方法［24］，GA的初始种群对算法搜索效率具有一定的影响。相比于完全随机的初始化，若初始种群已具有一定的聚类精度，同时种群的多样性又能较好地得到保持，则有利于局部搜索策略的局部搜索能力充分发挥，且减少了不必要的迭代，加速了算法收敛。与现有基于GA的网络聚类算法的随机初始化种群的方法不同，本文提出了基于连接强度的种群初始化方法(JSPI)。JSPI主要思路为:计算每个节点与网络已搜索到的社团的连接强度，并将该节点加入到连接强度最大的社团。

3 基于优化聚类方法的应用

3.1 CNM算法在优化RBF神经网络上的应用

在Newman提出的快速聚类算法的基础上，Clauset、Newman和Moore等人将堆的数据结构用在计算和更新复杂网络的模块度上，由此提出了一种新的贪婪算法，即CNM算法［25］，以此来优化 RBF神经网络。此算法的复杂度仅有O(n log2n)，非常接近线性复杂性。文献［15］根据CNM算法［25］提出了新的聚类算法，对数据集的先验知识可以完全的置之不理，然后还能自动进行社团的合并及分割是它最重要的特点。文献［26］的算法提出，合适的相似度量的选取最主要的是根据原始数据的特征来进行，此文献算法相似度量在算法的思想上选取的是欧式距离:

然后，想要得到它们间的相似度矩阵R，则必须根据欧式距离来对数据对象间的相似度进行计算。本文将CNM聚类算法优点充分的运用到对RBF神经网络的优化上面，进而形成了基于CNM聚类的RBF算法，相比较于基于k－均值的RBF算法，此方法在提高网络质量和稳定性上有了更好的改善，而且在精度上也得到了大大的提高。

3.2 在蛋白质相互作用网络中的应用

SCAN(Structural Clustering Algorithm for Networks)这种方法是由Mutlu Mete等人首先运用到复杂生物网络上的，能够很好地从复杂网络中寻求出簇和每一个功能模块，还能够以结点的形式把所取结构分类为不一样的角色(比如Hubs和Outliers)。采用芽酵母蛋白质交互网络做了一个分析实验，并且对比了其中的簇和原本的功能蛋白质。这样就证明了此算法的有效性，并且验证了聚类结果，由此可以验证预测的功能模块有着很好的纯度。经过后来学者的分析得出，此算法属于线性时间算法。后来，Mutlu Mete等人把SCAN算法与经典的CNM算法做了一个对比分析，有效地检测出了基因本体项(GO terms)所注释的功能组有最小p值的前10个簇，从这能看出SCAN算法比CNM算法能更精确地分割网络。

4 总结与展望

本文对经典和最新的基于优化的聚类方法进行了对比分析，得出以下结论:虽然经过各国学者的多年研究，但复杂网络聚类问题还存在诸多亟待解决的问题:(1)网络簇结构的本质含义一直没有被理解透彻。包括网络簇结构的形成经过;与网络其他复杂现象的联系如何;与网络自身的哪一类内在属性相互关联;(2)现今研究的复杂网络聚类方法只能同时满足计算速度、聚类精度高、无监督(即不依赖先验知识、对参数不敏感)中的一种，存在着局限性。通过定性和定量分析，比较现有主要研究方法就可看出，具有很高时间复杂性的方法一般是聚类精度高的方法，但如果计算速度加快，那么精度就会降低，对参数和先验知识的需求也会增加;(3)伴随复杂网络聚类方法的发展，其应用范围也逐渐拓宽，这对复杂网络聚类方法的要求也逐渐提高。如今的复杂网络聚类方法已经比较陈旧，也出现了很多相关问题，诸如动态复杂网络聚类、高维复杂网络聚类和分布式复杂网络聚类等;设计出基于特殊类型的复杂网络的新型复杂网络聚类方法。

［1］汪小帆.复杂网络理论及其应用［M］.北京:清华大学出版社，2006.4 －5.WANG Xiao－fan.Complex Network Theory and Its Application［M］.Beijing:Tsinghua University Press，2006:4－5.

［2］Duch J，Arenas A.Community Detection in Complex Networks using Extreme Optimization.Physical Review E，2005，72(2):027104.

［3］杨博，刘大有，LIU Jiming等.复杂网络聚类方法［J］.软件学报，2009，20(1):54 －66.YANG Bo，LIU Da － you，LIU Jiming，et al.Complex Network Clustering Method［J］.Journal of Software，2009，20(1):54 －66.

［4］潘幕，金杰，王崇骏等.社会网络中基于局部信息的边社团挖掘［J］.电子学报，2013，40(11):2255 －2263.PAN Mu，JIN Jie，WANG Cong － jun，et al.Local Information based Side Community Mining in Social Networks［J］.Journal of Electronic，2013，40(11):2255 －2263.

［5］Kim Y，Jeong H.Map Equation for Link Communities［J］.Physical Review E，2011，84(2):026110.

［6］HUANG Lei，WANG Guo，WANG Yang，et al.Link Clustering with Extended Link Similarity and EQ Evaluation Division［J］.PloS one，2013，8(6):e66005.

［7］LEI Xin，WU Shu，Ge Lei，et al.Clustering and Overlapping Modules Detection in PPI Network based on IBFO［J］.Proteomics，2013，13(2):278 －290.

［8］Lancichinetti A，Fortunato S.Benchmarks for Testing Community Detection Algorithms on Directed and Weighted Graphs with Overlapping Communities［J］.Physical Review E，2009，80(1):016118.

［9］Pizzuti C，Rombo S E.Algorithms and Tools for Protein－Protein Interaction Networks Clustering，with a Special Focus on Population － based Stochastic Methods［J］.Bioinformatics，2014，30(10):1343－1352.

［10］ZHOU Dong，Councill I，Giles CL.Discovering Temporal Communities from Social Network Documents.In:Shi Y，Clifton CW，eds.Proc.of the 7th IEEE Int’l Conf.on Data Mining.New York:IEEE Society，2007.745－750.

［11］JIN Dong.Genetic Algorithm with Local Search for Community Mining in Complex Networks［A］.Proceedings of the 22th International Conference on Tools with Artificial Intelligence(ICTAI’10)［C］.Arras，France:IEEE Press，2010.105 －112.

［12］Leskovec J.Statistical Properties of Community Structure in Large Social and Information Networks［A］.Proceedings of the 17th International Conference on World Wide Web(WWW’08)［C］.Beijing，China:ACM Press，2008.695－704.

［13］汪小帆，刘亚冰.复杂网络中的社团结构算法综述［J］.电子科技大学学报，2009，38(5).WANG Xiao－fan，LIU Ya－bin.Overview of Community Structure Algorithms in Complex Networks［J］.Journal of Electronic Science and Technology University，2009，38(5).

［14］Guimera R，Amaral Lan.Functional Cartography of Complex Metabolic Networks. Nature，2005，433(7028):895－900.

［15］郭陶.一种改进的加权复杂网络聚类方法［J］.计算机科学，2012，39(6A).GUO Tao.An Improved Weighted Complex Network Clustering Method［J］.Computer Science，2012，39(6A).

［16］Newman MEJ.Detecting Community Structure in Networks.European Physical Journal(B)，2004，38(2):321－330.

［17］Newman MEJ.Fast Algorithm for Detecting Community Structure in Networks.Physical Review E，2004，69(6):066133.

［18］Reichardt J，Bornholdt S.Detecting Fuzzy Community Structures in Complex Networks with a Potts Model.Physical Review Letters，2004，93(19):218701.

［19］LI S Z，CHEN Y H，DU H F，et al.A Genetic Algorithm with Local Search Strategy for Improved Detection of Community Structure［J］.Complexity，2010，15(4):53－60.

［20］李峻金，向阳，牛鹏等，一种新的复杂网络聚类算法［J］.计算机应用研究，2010，27(6).LI Jun － jin，XIANG Yang，NIU Peng，et al.A New Clustering Algorithm for Complex Networks［J］.Computer Application Research，2010，27(6).

［21］金弟，刘大为，杨博等，基于局部探测的快速复杂网络聚类算法［J］.电子学报，2011，11(2540 －2545).JIN Di，LIU Da － wei，YANG Bo，et al.Fast and Complex Network Clustering Algorithm based on Local Detection［J］.Journal of Electronic，2011，11(2540 －2545).

［22］孔令旗，杨梦龙.符号网络聚类算法FEC的改进［J］.计算机应用，2011，31(5).KONG Lin － qi，YANG Meng － long.Improvement of FEC for Clustering Algorithm of Symbol Network［J］.Computer Application，2011，31(5).

［23］Radicchi F，Castellano C，Cecconi F，et al.Defining and Identifying Communities in Networks［J］.Proceedings of the National Academy of Science，2004，101(9):2658－2663.

［24］丁转莲.基于优化的复杂网络聚类方法研究［D］.安徽:安徽大学，2014.DING Zhuan － lian.Research on Clustering Method of Complex Network based on Optimization［D］.Anhui:Anhui University，2014.

［25］Newman MEJ.Fast Algorithm for Detecting Community Structure in Networks［J］.Physical Review E，2004，69(6):066133.

［26］丁孝燕.复杂网络聚类及其在神经网络中的应用研究［D］，广西:广西师范学院，2011.DING Xiao－ yan.Complex Network Clustering and Its Application in Neural Networks［D］.Guangxi:Guangxi Teachers Education University，2011.

［27］Mete M，TANG F，XU X，et al.A Structural Approach for Finding Functional Modules from Large Biological Networks［J］.BMC Bioinformatics，2008，9(9).

［28］Clauset A，Newman M，Moore C.Finding Community Structure in Very Large Networks［J］.Phys Rev E，2004，70.

［29］Havemann F，Glaser J，Heinz M，et al.Identifying O-verlapping and Hierarchical Thematic Structures in Networks of Scholarly Papers:A Comparison of Three Approaches［J］.PloS one，2012，7(3):e33255.

［30］Solava R W，Michaels R P，Milenkovic T.Graphletbased Edge Clustering Reveals Pathogen－Interacting Proteins［J］.Bioinformatics，2012，28(18):i480 －i486.

［31］HE D，JIN D，Baquero C，et al.Link Community Detection Using Generative Model and Nonnegative Matrix Factorization［J］.PLOS ONE，2014，9(1):e86899.