WSN中一种新的锚节点分布方式*

赵建平，马淑丽，刘凤霞，厉成远

(曲阜师范大学物理工程学院，山东 曲阜 273165)

0 引言

无线传感器网络由微型传感器节点和控制系统、无线通信系统等组成，一般应用在军事、环境检测［1］、森林防火、海洋等人不能够长时间滞留的环境中，所以微型传感器未知节点一般是从飞机上抛散，服从随机分布。而锚节点的部署是已知的。未知节点位置信息的获取对无线传感器网络的信息跟踪等服务功能起着关键作用。节点定位的理论研究中，研究者一般采用节点随机均匀分布方式仿真。现有的节点定位算法主要分为:基于测距的定位算法和无需测距的定位算法，以及两者的结合等。基于测距的节点定位算法定位精度高但是需要复杂的硬件设备等，成本高，而无需测距的节点定位算法简单成本低，但是定位精度不高，往往满足不了一些高定位精度要求的应用。本文考虑提高无需测距算法的定位精度，提出一种新的锚节点人工部署方式，并分别在二维、三维空间仿真分析对DV－Hop算法节点定位精度的影响。

1 概述

1.1 DV －Hop算法

DV－Hop定位算法是一种无需测距的节点定位算法，由美国罗格斯大学Dragos Niculescu等人提出［2］。

无线传感器网络是同构的网络［3］。每个节点的通信半径等是相同的，节点间的通信是双向的，采用自由空间电波传播模型，辐射范围是以自身为原点的圆(二维)或球(三维)。每个节点有自己的ID号。锚节点的位置是已知的，定位开始先将自己的位置信息与初始跳数值信息等以泛洪方式广播至整个网络，每被转发一次跳数值加一。根据锚节点间的实际距离除以节点间的跳数估算各自的平均每一跳距离并作为校正值广播。未知节点定位时只将离自己最近的锚节点的校正值作为自己与其他锚节点的平均每跳距离。当知道至少三个(二维)或者四个(三维)锚节点与未知节点的估算距离时，就可以用三边测量法或极大似然估计法等进行未知节点位置估算。最终得到未知节点坐标信息。

1.2 极大似然估计法原理

以三维空间节点定位为例，如图1所示［3］。

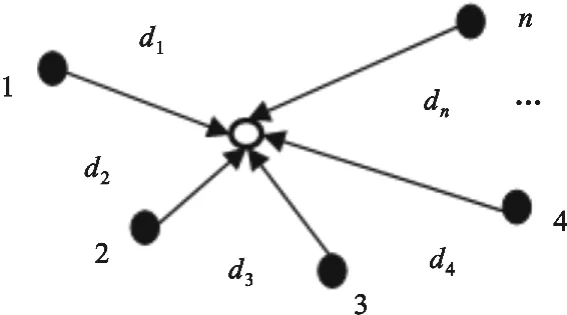
图1 极大似然估计法示意

已知1、2、3 等 n 个锚节点坐分别标为(x1，y1，z1)、(x2，y2，z2)、(x3，y3，z3)、…、(xn，yn，zn)，未知节点到锚节点距离分别为d1、d2、d3、…、dn，根据以下式子，最终估算出未知节点坐标(x，y，z):

将式(1)前(n－1)个方程分别减去最后一个方

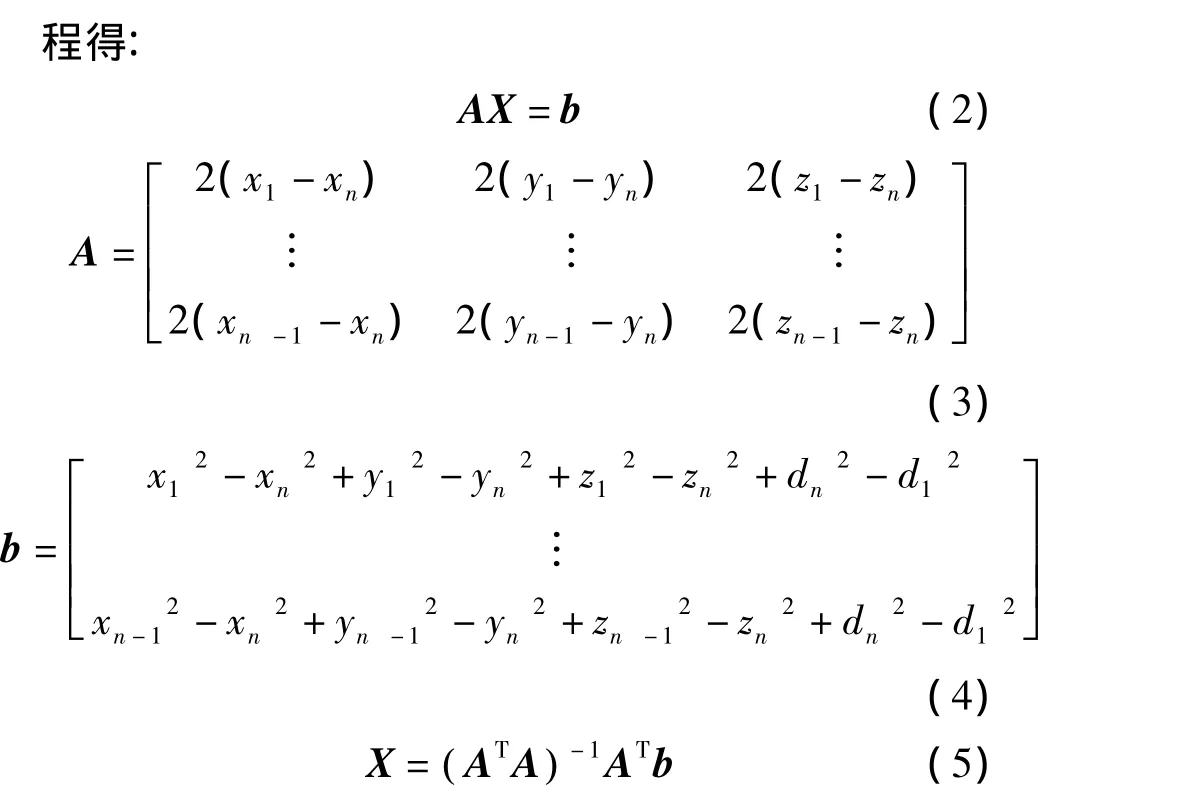
1.3 研究现状

现在许多研究者从改进二维空间节点定位算法方面提高DV－Hop算法节点定位精度。如文献［4］在二维区域提出改进的DV－Hop算法，通过小波神经网络算法修正平均每一跳距离值，提高了节点定位精度。而在无线传感器网络的实际应用中三维节点定位应用更多。文献［1］在三维无线传感器网络空间以DV－Hop算法为基础建立空间向量模型，提高了定位精度。

从锚节点部署策略方面考虑提高定位精度的文献较少。许多文献如文献［4］采用未知节点与锚节点随机分布的仿真环境。文献［5］研究了圆形区域内节点分布均匀性对定位精度的影响，并在其提出的圆形均匀分布领域内用三种无需测距的算法仿真。文献［6］指出基于无需测距的DV－Hop定位算法的定位精度受限于网络中节点分布的均匀性。文献［7－8］各提出了一种均匀二维锚节点分布方式:利用欧式范数，根据式(5)推导出相对定位误差最小时(推导过程见文献［8］)，其锚节点分布满足下式:

式中，(xm，ym)为中心锚节点坐标，(xi，yi)为其他锚节点坐标，即一个锚节点分布在圆形区域中心，其他锚节点对称分布在区域周边。

本文提出一种新的二维、三维锚节点分布方式，分别将所有锚节点固定在正方形内切圆、立方体内切球的中心，经研究发现能大大提高节点定位精度。

1.4 其他

绝对误差，即节点的定位误差，指未知节点i的定位坐标(xi，yi)与实际坐标(x0i，y0i)的距离，如下式:

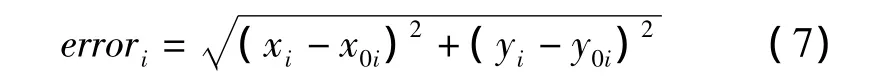
定位精度，指网络中全部节点(N个)的平均定位误差与节点通信半径R的比率，值越小定位精度越高，如下式:

网络连通度C，反应网络中节点的通信密度，由网络区域的边长L、节点通信半径R、节点总数N决定。二维网络连通度、三维网络连通度计算式子分别如式(9)、式(10)所示:

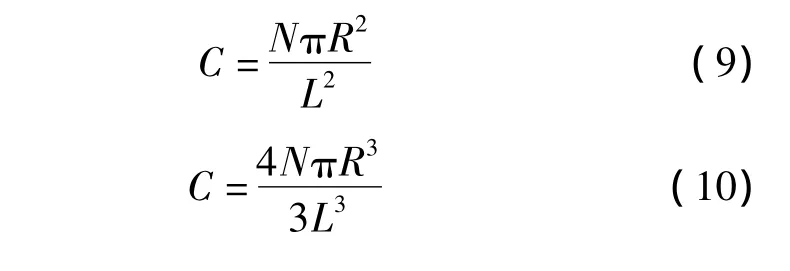
2 本文提出的锚节点分布方式

2.1 二维空间

文献［5］根据节点的通信辐射范围是以自身为原点的圆(二维)，将未知节点规定为圆心位置，锚节点在扇形区域内均匀分布，并用3种无需测距的定位算法验证能提高定位精度。本文规定锚节点为圆心位置，其他未知节点在扇形区域内随机均匀分布。

首先将无线传感器网络监控区域划分为n2(4、9、16、25、36、49 等)个相同的小正方形几何区域，在每个小正方形区域的内切圆中心位置放置1个锚节点。未知节点在网络监控区域内随机均匀分布。

设定仿真环境在二维空间边长为100 m的正方形。二维锚节点分布方式如图2所示。

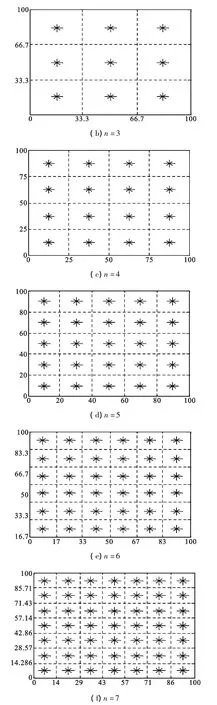
图2 本文二维锚节点分布 n=2、3、4、5、6、7

2.2 三维空间

将三维空间划分为n3(8、27、64等)个相同小立方体空间，在每个空间的内切球中心位置放置1个锚节点，其他未知节点采用随机均匀分布方式。

设定仿真环境在三维空间边长为100 m的正方体。三维锚节点分布方式与文献［1］随机分布方式如图3所示。

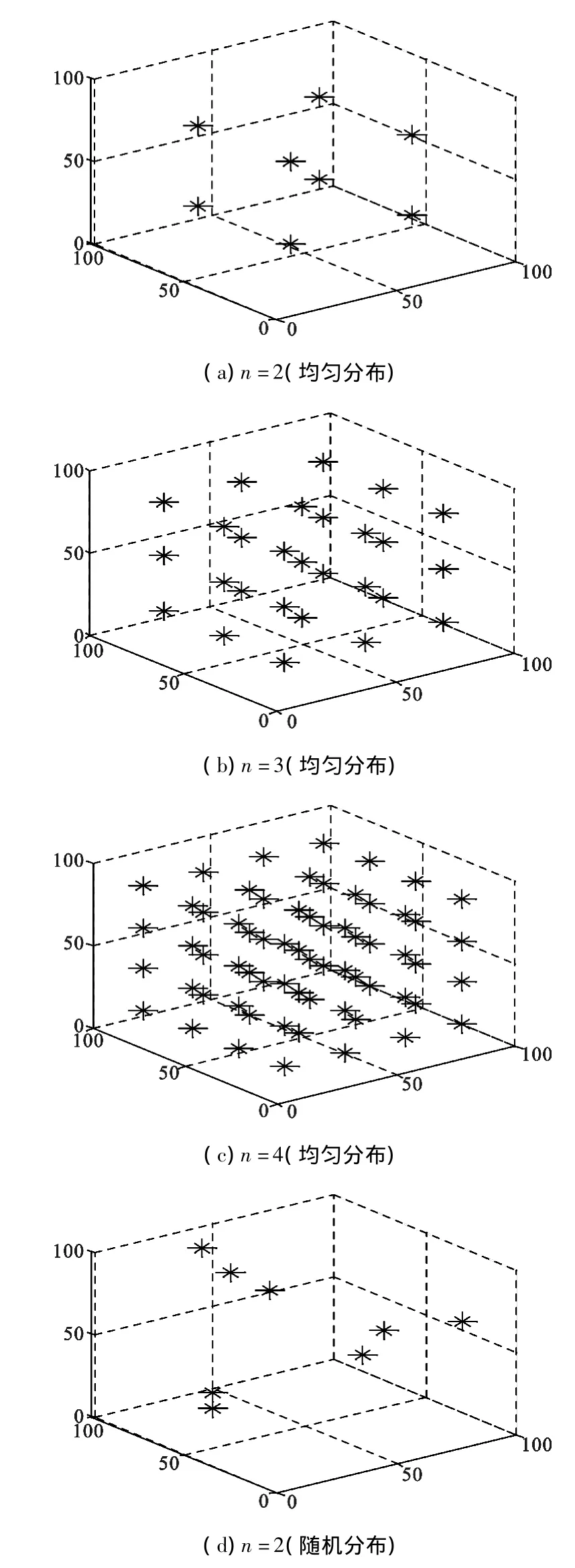
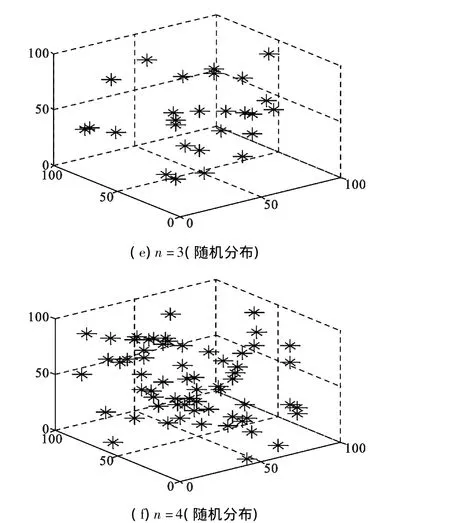
图3 本文三维锚节点分布与随机分布n=2、3、4

3 二维仿真结果分析

3.1 5种锚节点人工部署方式

文献［5］给出的锚节点最直观的均匀分布模型为:在边长为M m的正方形中分布m个锚节点，锚节点间是等间距的，相距 M/(m0.5－1)m。文献［7］提出1个锚节点分布在区域中心其他锚节点横纵坐标呈等差数列分布在区域的边上。文献［8］提出1个锚节点在区域中心，其他锚节点分布在以区域中心为圆心以区域边长的一半为半径的圆上。文献［4］的节点分布方式是将节点全部随机分布。

将仿真环境设定在边长100 m正方形区域内，分别按本文、文献［5］、文献［4］的锚节点分布方式布置36个锚节点，其他64个未知节点随机分布。将上述3种节点分布方式对比，如图4所示。

图4 3种二维节点分布方式m=36

通信半径取21 m，在3种节点分布方式下做DV－Hop算法的定位。3种节点分布方式中未知节点位置分布相同，并从1到64编号。每个节点定位误差如图5所示。

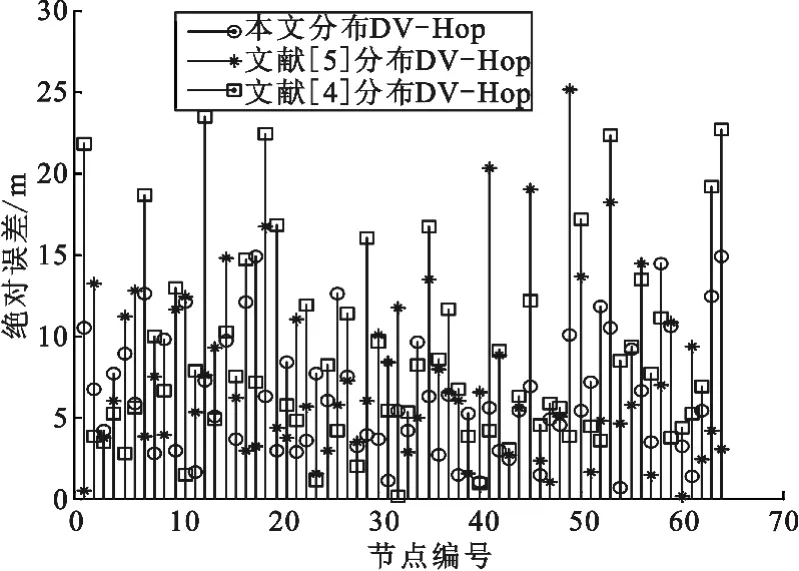
图5 三种分布方式节点定位误差R=21

由于节点分布的随机性，将程序运行1000次取平均值，得出锚节点覆盖率36%，网络连通度为13.85时，本文提出的节点分布方式定位精度比文献［5］、文献［4］分布方式分别提高4%、9.6%。

分别按本文、文献［7－8］节点分布方式布置9个锚节点，其他91个未知节点随机分布。如图6所示。

图6 三种二维节点分布方式m=9

做DV－Hop算法的定位误差对比，如图7所示。

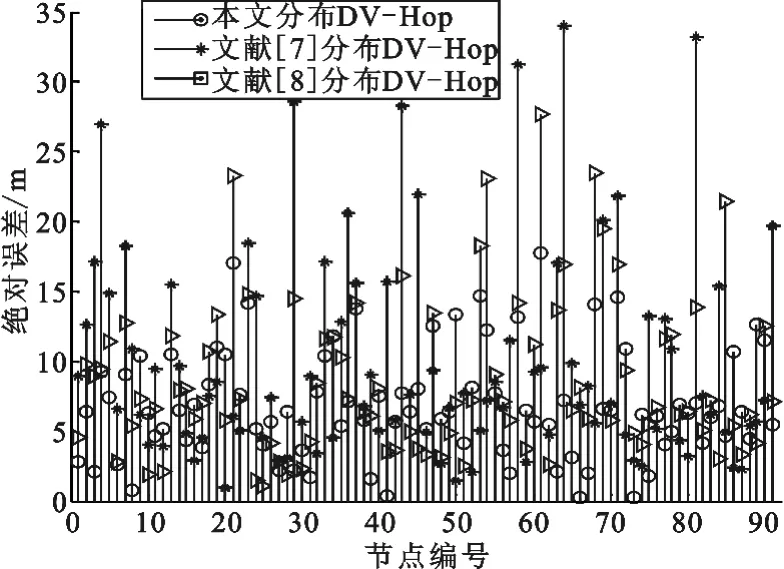
图7 三种分布方式节点定位误差R=21

将程序运行1000次取平均值，得出锚节点覆盖率9%，网络连通度为13.85时，本文提出的节点分布方式定位精度比文献［7－8］分布方式分别提高6.1%、1.3%。

3.2 锚节点为9、16时不同通信半径下对比

锚节点为9时，节点通信半径分别取19、22、25、28、31、34、37、40、43、46、49 m。用 DV －Hop 算法对本文与文献［4］两种环境中不同通信半径下节点定位精度。程序运行1000次取平均值，如图8所示。

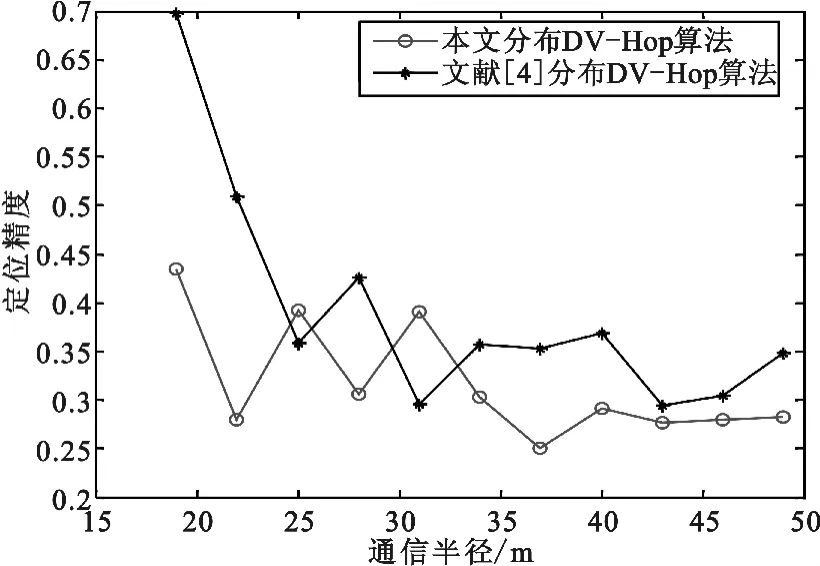
图8 两种分布不同通信半径定位精度m=9

锚节点覆盖率为9%时，本文分布方式在通信半径为22 m、28 m时定位精度分别比文献［4］提高约23%、12%，通信半径为37 m时定位精度最高达到24.99%，比文献［4］提高约10.2%。

锚节点为16个时，将程序运行1000次取平均值，如图9所示。

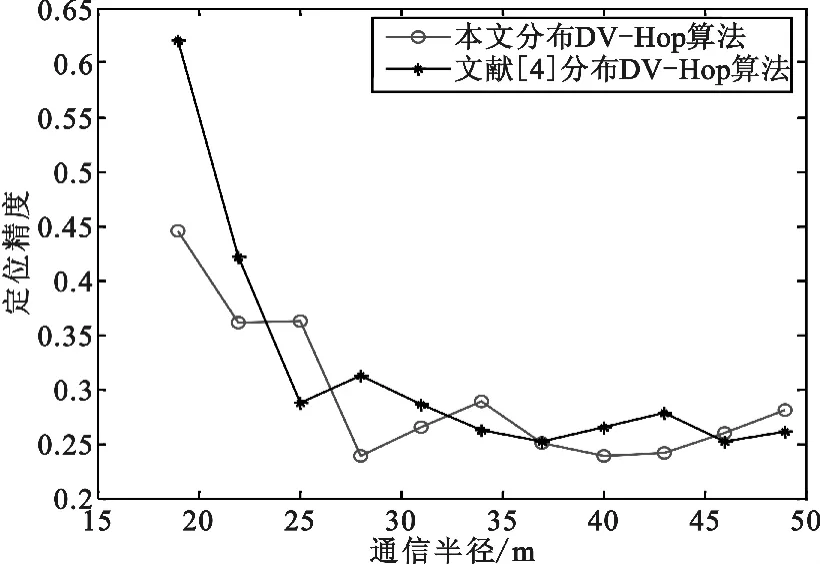
图9 两种分布不同通信半径定位精度m=16

锚节点覆盖率为16%时，本文分布方式在通信半径在28 m时定位精度最高达到23.8%，比文献［4］分布方式定位精度提高约7.4%。

无线传感器网络中节点通信半径越低节点能量消耗越小［9］，本文节点分布方式能在二维区域锚节点覆盖率9%时通信半径22、28、37 m时和锚节点覆盖率为16%时通信半径在19、22、28、31 m时定位精度比文献［4］节点分布下定位精度明显要高，所以本文节点分布方式在选择合适的锚节点覆盖率时选择较低的通信半径能降低节点能量消耗，延长网络生命周期。

3.3 通信半径为28 m、37 m时不同锚节点覆盖率

通信半径为28 m时，锚节点覆盖率分别取4%、9%、16%、25%、36%、49%，比较不同锚节点覆盖率下本文与文献［4］节点分布方式对DV－Hop算法定位精度的影响，将程序运行1000次取平均值，如图10所示。

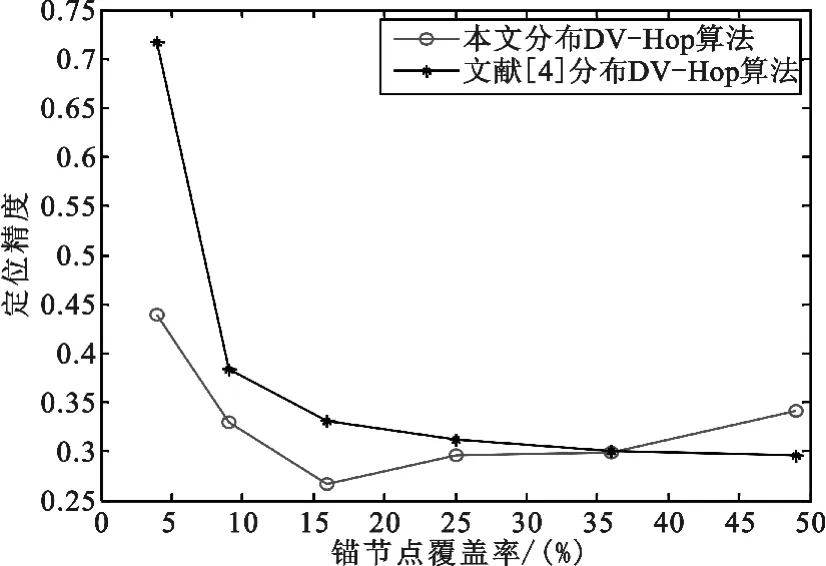
图10 两种分布不同锚节点覆盖率定位精度R=28

通信半径为28 m时，本文节点分布方式在锚节点覆盖率36%以下时定位精度比文献［4］分布方式明显要高。锚节点覆盖率4%时，本文节点分布方式比文献［4］分布方式定位精度提高27.8%。锚节点覆盖率16%时定位精度最高达到26.7%，比文献［4］节点分布方式定位精度提高约7%。

通信半径为37 m时，将程序仿真运行5000次取平均值，如图11所示。

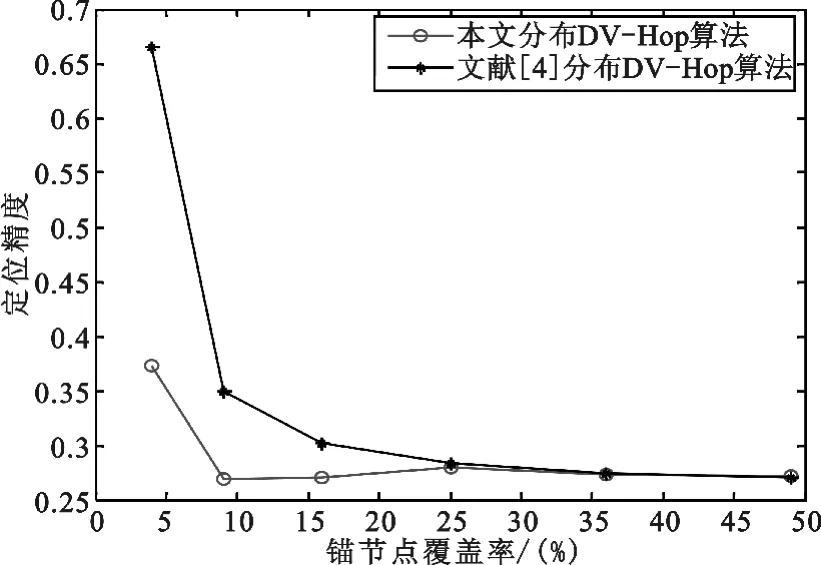
图11 两种分布不同锚节点覆盖率定位精度R=37

通信半径为37 m时，在不同锚节点覆盖率下本文节点分布方式比文献［4］分布方式定位精度高。随着锚节点覆盖率增大两种分布方式下的定位精度都提高，且逐渐逼近，节点覆盖率在9%、16%时本文节点分布方式定位精度分别达到26.9%、27.4%，比文献［4］分布方式下定位精度分别提高约8%、3.2%。

由于锚节点微型传感器自带导航装置成本比普通节点高［10］，本文节点分布方式在通信半径为28 m、37 m二维区域低锚节点覆盖率时能明显提高节点定位精度，所以本文分布方式在合适的通信半径下选择较低的锚节点覆盖率能降低无线传感器网络的成本。

3.4 不同通信半径和不同锚节点个数对比

经实验发现，通信半径越大、锚节点覆盖率越高节点定位精度总体趋势越好。锚节点覆盖率取4%、9%、16%、25%、36%、49%，节点通信半径取21、24、27、30、33、36、39、42、45、48 m。求两种分布方式下DV－Hop定位精度之差，运行1000次，如表1所示(加号表示提高定位精度，负号表示降低定位精度)。

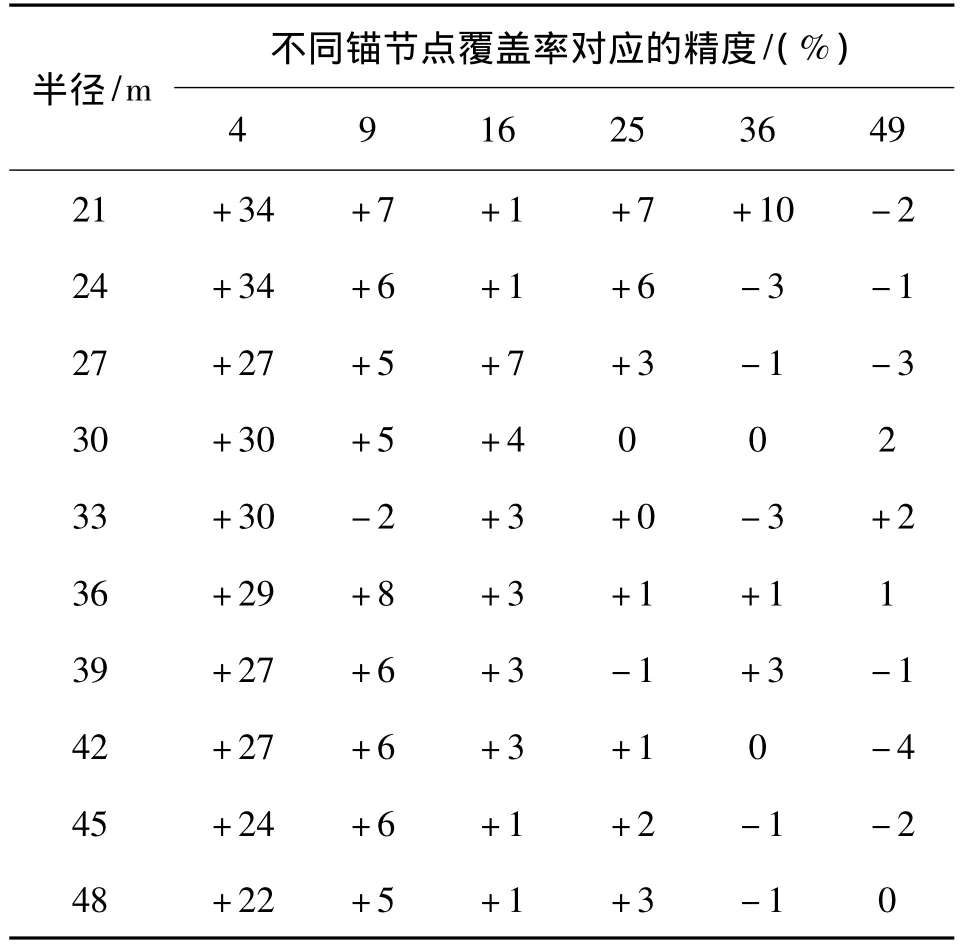
表1 文献［4］分布不同锚节点覆盖率不同通信半径下与本文分布定位精度差值

如表1所示，本文节点分布方式在较低的锚节点覆盖率与较低的通信半径下比文献［4］节点分布方式定位精度高。说明本文节点分布方式在提高节点定位精度同时能降低无线传感器网络成本和延长网络生命周期。

4 三维仿真结果与分析

(1)锚节点27个时不同通信半径下不同未知节点个数对比

在三维空间，锚节点个数取27个，边长为100 m的正方体内，未知节点个数取 100、200、300、400、500，通信半径取 30、32、34、36、38、40、42、44、46、48 m，分别按本文锚节点分布方式和文献［1］锚节点分布方式布置锚节点，其他未知节点分布采用随机分布方式且相同。在不同通信半径、不同未知节点个数下对两种节点分布方式做三维DV－Hop算法定位精度对比。仿真3000次，取平均值，如图14和图15所示。

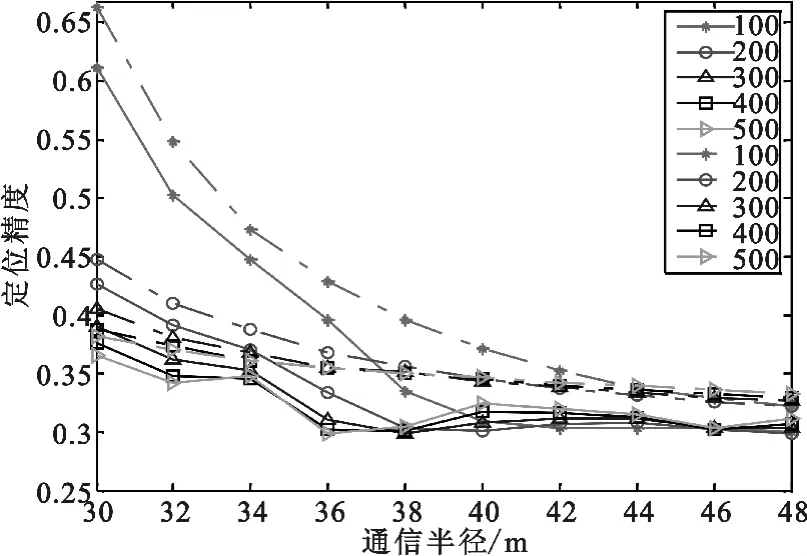
图14 两种分布不同通信半径下不同未知节点数m=27

从图14中看出本文节点分布方式定位精度比文献［1］分布方式高。随着通信半径增大，两种方式定位精度在相同未知节点个数下总体趋势提高。通信半径小于等于38 m时未知节点个数多的定位精度占优势，随着通信半径增大，未知节点个数少的定位精度占优势，在40 m时500个未知节点的定位精度与100、200的定位精度明显拉大。

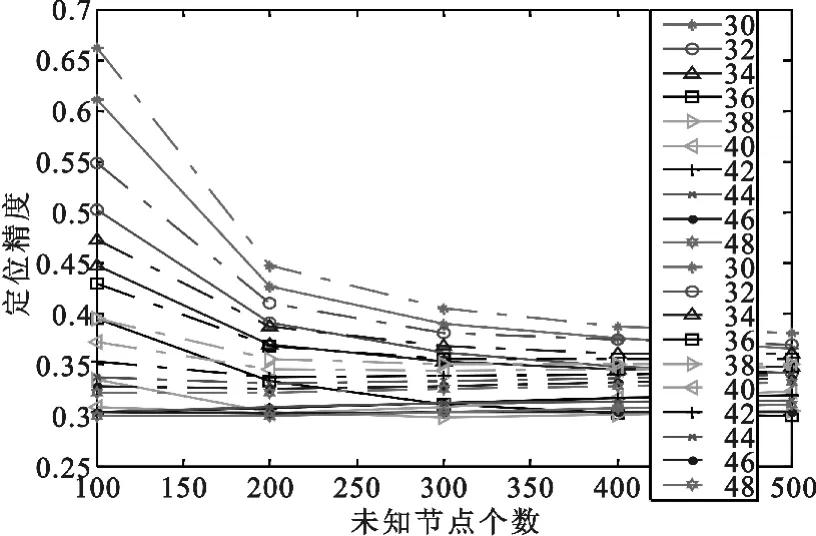
图15 两种分布不同未知节点数下不同通信半径m=27

从图15中看出随着未知节点个数的增多，两种方式下定位精度都逐渐提高并趋于平缓，且在相同的通信半径和相同的未知节点个数下本文提出的节点分布方式比文献［1］分布方式定位精度都要高。

在通信半径较小、未知节点个数较少时，本文节点分布方式比文献［1］节点分布方式能提高节点定位精度(如表2所示)。证明在三维空间锚节点数为27时，本文节点分布方式能提高定位精度的同时降低网络成本和延长网络生命周期。

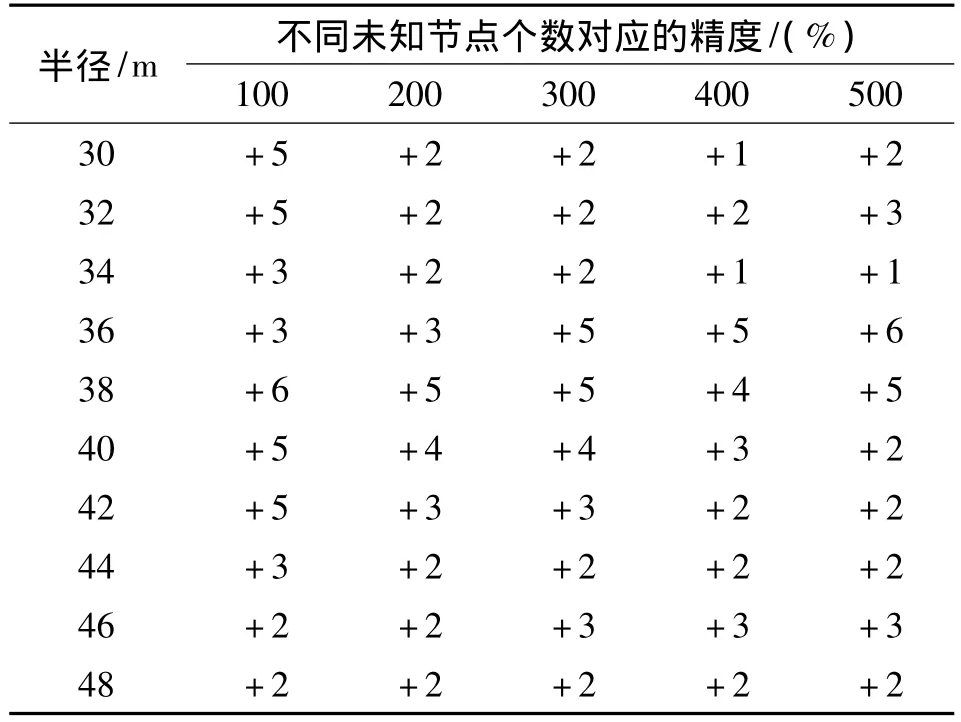
表2 文献［1］分布不同未知节点个数不同通信半径下与本文分布定位精度差值(m=27)

(2)锚节点64个时不同通信半径、不同未知节点个数定位精度对比

锚节点个数64时，未知节点个数取100、200、300、400、500、600、800、1000，通信半径 28、30、32、34、36、38、40、42、44、46 m。求两种分布方式下DV－Hop定位精度之差，仿真3000次，如表3所示。

表3 文献［1］分布不同未知节点个数不同通信半径下与本文分布定位精度差值(m=64)

由表3可知，本文节点分布方式能在较低的未知节点个数和较小的通信半径下提高定位精度，说明锚节点数为64时，本文节点分布方式在三维空间也能降低网络成本和延长网络生命周期。

5 结语

本文首先将提出的一种锚节点人工部署方式与其他文献锚节点人工部署方式对比，仿真证明有一定的优势，然后分别在二维、三维空间下比较不同的锚节点覆盖率、不同的通信半径、不同未知节点数等仿真新的锚节点分布方式对DV－Hop算法的定位精度影响规律。MATLAB仿真结果表明本文的节点分布方式在节点数低、通信半径较小时能有效提高节点定位精度。新的锚节点分布方式能降低网络成本和节点能量消耗，适用于一定的无线传感器网络应用中，缺点是增加了人力负担。下一步用基于无需测距的质心定位算法验证本文提出的节点分布方式。

［1］YAN Zang，SUN Bai－ xiang，GUO Wei，LI Ming.Research on Node Localization for Wireless Sensor Networks［C］//Electric Engineering and Computer(MEC)，2013 IEEE International Conference on Mechatronic Sciences.IEEE，2013:3665 －3668.

［2］陈敏，王擘，李军华.无线传感器网络原理与实践［M］.北京:化学工业出版社，2011.CHEN Min，WANG Bo，LI Jun－hua.Wireless Sensor Network Theory and Practice［M］.Beijing:Chemical Industry Press，2011.

［3］姚向华，杨新宇，易劲刚等.无线传感器网络原理与应用［M］.北京:高等教育出版社，2012.YAO Xiang－hua，YANG Xin－yu，YI Jin－gang，et al.Wireless Sensor Network Principle and Application［M］.Beijing:Higher Education Press，2012.

［4］HU Juan，JIANG Min－lan.An Improved Node Localization Algorithm in Wireless Sensor Network［C］//Workshop on Advanced Research and Technology in Industry Application(WARTIA)，IEEE ，2014:398－401.

［5］宫娜娜，武海艳.传感器网络节点分布均匀性与定位性能的关系［J］.电子测量技术，2014，37(12):80－85.GONG Na－na，WU Hai－yan.The Relationship Between the Sensor Network Node Distribution Uniformity and Positioning Performance［J］.Electronic Measurement Technology，2014，37(12):80－85.

［7］黄炎炎，陈向东，倪进权等.改进的DV－HOP无线传感器网络定位算法［J］.通信技术，2014，47(07):765－769.HUANG Yan－yan，CHEN Xiang－dong，NI Jin－quan，et al.An Improved DV －Hop Localization Algorithm for Wireless Sensor Networks［J］.Communications Technology，2014，47(07):765－769.

［8］ZHENG You－si，WAN Lei，SUN Zhi，MEI Shun－liang.A Long Range DV －Hop Localization Algorithm with Placement Strategy in Wireless Sensor Networks［C］//Wireless Communications，Networking and Mobile Computing，2008.WiCOM'08.4th International Conference on.［s.l.］:IEEE，2008:1 －5.

［9］刘方爱，张春花，吴楠.WSN中基于能量和距离的自适应分层路由算法［J］.计算机应用研究，2014，31(11):3434－3437.LIU Fang－ai，ZHANG Chun－hua，WU Nan.Adaptive Hierarchical Routing Algorithm for WSN based on Energy and Distance［J］.Application Research of Computers ，2014，31(11):3434 －3437.

［10］姚英彪，姜男澜.无线传感器网络定位的分布式求精算法［J］.通信学报，2015，36(01):1－10.YAO Ying－biao，JIANG Nan－lan.Distributed Refinement Algorithm for WSN Localization［J］.Journal on Communications，2015，36(01):1 －10.