一种在FTN系统下的低复杂度判决反馈均衡器*

徐 洋，郭明喜，沈越泓，段 昊，张 胜

0 引言

FTN理论虽然早在1975年就已经提出［1］，但直到现在它仍然受到国内外学者的广泛关注。因为在相同比特能量、相同的时间、相同的带宽、相同的误码率的条件下，FTN系统可以比传统的Nyquist系统多传输30% ～100%的数据［2］。这对于频域资源非常紧张的现代社会是非常有用的。但是，FTN系统的符号速率超过了Nyquist速率，不可避免地引入了严重的ISI。这将大大增加通信设备特别是接收机的复杂度。

为了解决这个问题，很多复杂度相对较低的解决方案被引入FTN系统中，如维特比算法［3］、连续串扰消除算法(SIC)、加窗Chase均衡器、频域均衡器等。就频域均衡器而言，目前已经提出的有线性频域均衡器(FDE)［4］和迭代分组频域判决反馈均衡器(IBDFE)［5］。这些均衡器基于频域是因为在受ISI影响的系统中，相比于时域均衡器，频域下的均衡器操作可以使系统在保持性能不变的情况下有效降低复杂度［6］。而在频域均衡中，非线性均衡器在消除ISI上的性能要优于线性均衡器［7］。

本文在意大利著名学者N．Benvenuto和S．Tomasin 2014年给出的IBDFE基础上提出了LC－IBDFE。该均衡器基于频域，遵循MMSE准则。LCIBDFE通过将判决信号中的误差与期望信号分离，引入判决错误符号的方差 σ2Ξ(l－1)，预定义 SER 等方法简化了均衡器抽头系数的计算，从而有效降低了复杂度，实现性能与复杂度更好的折衷。

1 系统模型和IBDFE的简要分析

1． 1 FTN系统模型

本文首先构建一个常用的FTN通信系统模型:令系统发送滤波器的冲激响应是gT(t);接收滤波器的冲激响应是gR(t);发送滤波器、接收滤波器和信道响应卷积后的冲激响应是h(t);发送滤波器与信道卷积后的冲激响应是hTC(t)。因此在系统的发送端，发送符号可表示成:

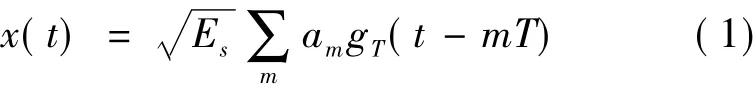
式中，am，m=0，1，…，N 表示信息符号;T= ρTs表示发送符号的时间间隔，因此1/T是符号的发送速率，其中1/Ts是该系统的Nyquist速率;ρ(0＜ρ≤1)是时间加速因子。在FTN系统中，实际上ISI是无限长的，但是为了方便接收端的有限长均衡器操作，需要对ISI做近似截短处理，将无限的ISI截短成有限长，设截短后的 ISI长度是 Nh［4］。

经过加性高斯白噪声(AWGN)信道后，接收端对信号匹配滤波并采样。为了获取到足够多的信号的统计信息，令接收端以2倍的发送速率采样，即采样速率设为2/T。设si是过采样后的am，则s2m=am，s2m+1=0，m=0，1，…，N。所以接收信号可表示成:

式中，hk=h(kT/2)，k=0，1，…，Nh－1。wi是噪声，它是加性高斯白噪声wINi与接收滤波器冲激响应gR(t)的卷积，其中加性高斯白噪声的功率谱密度是n0。

1． 2 IBDFE的简要分析

在使用IBDFE的系统中，首先发送端使用伪随机噪声(PN)扩展传输方式，这可以使冲激响应hk与si线性卷积可以等效成循环卷积［8］。在发送端，发送符号被组合成长度为(P－L)的数据信号分组{ dm}。然后在分组末端加上长度为L的伪随机噪声(PN)序列 { qm}，而 { qm}在接收端已知。其结构如图1所示。

图1 PN扩展后的信号分组

所以，信号分组可表示成:

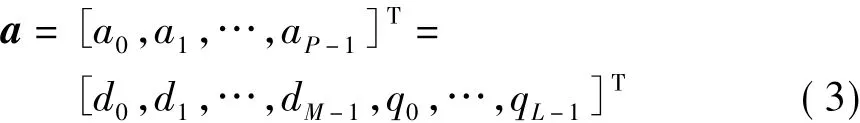
在接收端，考虑到过采样，信号分组长度会变成2P，分组中信息序列长度变成2M，PN序列长度变成2L。另外，除了伪随机噪声(PN)扩展传输方式，频域均衡器也可以采用循环前缀(CP)扩展传输方式［9－10］，这里不采用循环前缀(CP)，是因为伪随机噪声扩展在性能上更优秀［8］。

这里值得注意的是:为了保证相邻的两个分组内的数据符号不相互影响，PN序列长度L必须要大于等于ISI的长度，即:L≥(Nh－1)/2。另外，在发送第一个信号分组前，发送端还要先发送一个长度为L的PN序列。发送信号的结构图如图2所示。

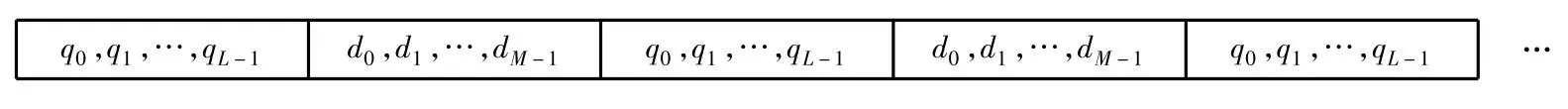
图2 发送信号分组的结构

发送的信号分组经过加性高斯白噪声信道(AWGN)后到达接收端。在接收端，IBDFE结构简图如图3所示。

图3 IBDFE结构

由图3可以看出IBDFE由两部分组成:前向滤波器和反向滤波器。接收到的信号 { xi}经过DFT变换，可以得到:

式中，p=0，1，…2P －1，其中 Xp，Sp，Hp分别是 xi，si，hp的2P点DFT变换。Wp是wi的2P点DFT变换，满足=。设迭代次数为l，最大迭代次数为NI，(l=1，2，…NI)则第 l次迭代后的信号表示成:

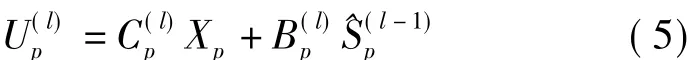
由文献［5］可得，该均衡器的反向抽头系数是:

式中，B(l)p+P=B(l)p，p=0，1，…，P －1。

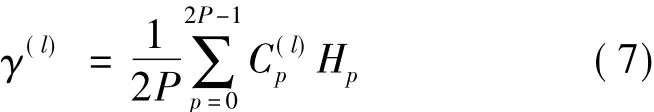
前向抽头系数是:

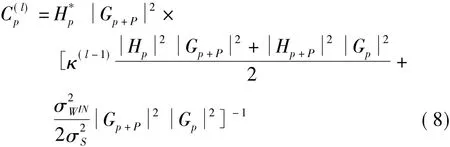
式中，Gp，Hp是周期为 2P 序列，即 Gp－P=Gp+P，Hp－P=Hp+P，p=P，P+1，…，2P －1。的估计参考文献［11］。

从式(6)、式(8)可以看出均衡器每进行一次迭代时，参数 r(l)S，^S和 σ2^S都要计算一次，这使均衡器的复杂度变得很高。因此，有必要研究一种低复杂度的接收结构来代替IBDFE。

2 LC-IBDFE抽头系数设计及其参数的简化估计

在接收机结构上，本文所提的LC－IBDFE与IBDFE结构相同。不同之处在于抽头系数的设计和参数估计。本文先将判决信号中的误差与期望信号分离，重新推导得出了抽头系数的计算式，并在此基础上讨论了降低复杂度的方法。

2． 1 抽头系数设计

为了降低复杂度，先将判决信号中的误差与期望信号分离，因此频域判决信号^S(l－1)p表示为:

式中，Ξ(l－1)p是第(l－1)次迭代的判决符号 ^S(l－1)p与期望符号Sp之间的频域判决误差。代入式(5)，可以得出:

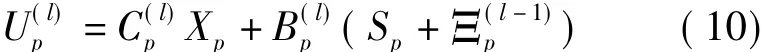
式中，0≤p≤2P－1，由MMSE准则可得:

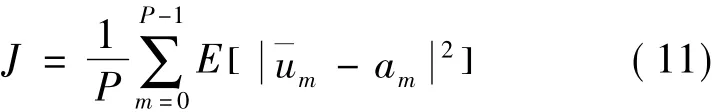
根据Parseval定理:

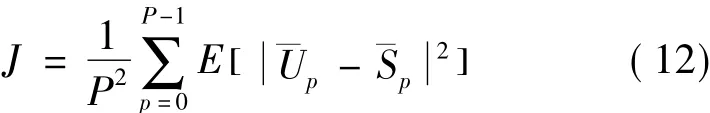
式中，¯Up=(U(l)p+U(l)p+P)/2，¯Sp=(Sp+Sp+P)/2=Sp。

将式(10)代入式(12)中，得

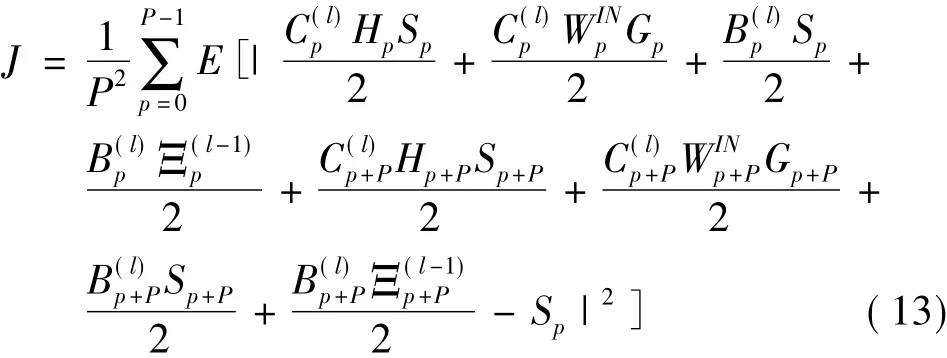
为了在消除ISI的同时不损失当前判决符号的信息，本文加入了约束条件［9－10］:

然后用拉格朗日乘数法将约束条件加入式(13)中，推导得到均衡器抽头系数

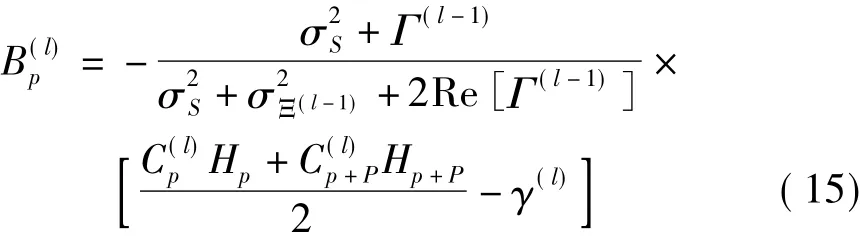
式中，令 B(l)p+P=B(l)p，p=0，1，…P －1［5］

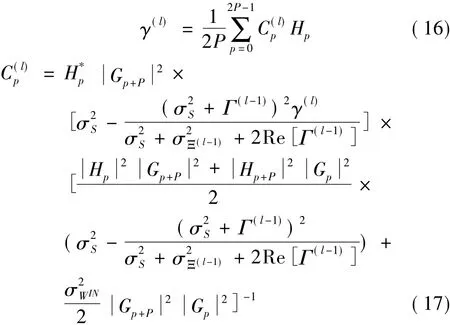
式中，Gp，Hp是周期为 2P 序列，即 Gp－P=Gp+P，Hp－P=Hp+P，p=P，…2P － 1，σ2S=PMa，σ2WIN=2PMwIN其中Ma是发送信号功率，MwIN信道中时域高斯白噪声功率。

将式(17)代入式(16)得:

其中:

2． 2 参数的简化估计

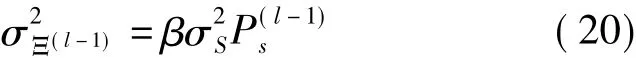
式中，β在QPSK、16PSK、64PSK中的值分别是2、2/5、2/21［11－12］，P(l－1)s是第(l－ 1)次迭代的 SER。为了简化复杂度，将P(l－1)s预定义成一个固定值，记为Ps，pre。但是需要注意的是，为了成功的使用判决反馈均衡器，第一次迭代经过线性均衡器后的SER必须要足够小，要小于一个门限。因此预定义的的值也一定要小于这个门限。第三部分将讨论如何设定 Ps，pre的值。

频域信号与判决误差的互相关Γ(l－1)也是由系统的调制方式和SER决定的。运用柯西不等式，Γ(l－1)可以表示为:

［12］得出:为了使DFE能可靠地检测接收符号，信号经过第一次迭代的线性均衡器后的SER应该小于一个门限值，参数Ps，pre合理的预设值也应该小于这个门限。而这个门限条件对于在FTN系统下的频域线性均衡器是可以达到的［4］，这意味着 Γ(l－1)＜ ＜ σ2S［12］。因此式(15)、式(17)中的项 Γ(l－1)、2Re［Γ(l－1)］可以忽略，因此:

表1 在 ρ=0．8、NI=3、SNR=10 dB的条件下 Ps，pre分别取不同值时 LC －IBDFE的性能

2． 3 LC-IBDFE抽头系数简化设计

由式(20)可知，σ2Ξ(l－1)＜ ＜ σ2S［11－14］。由此可

得:

将式(22)～式(25)代入式(19)得:

因此，简化后的DFE反向抽头系数是:

由式(28)可知 B(l)p=B(l)p+P，p=0，1，…P －1。

简化后的DFE前向抽头系数是:

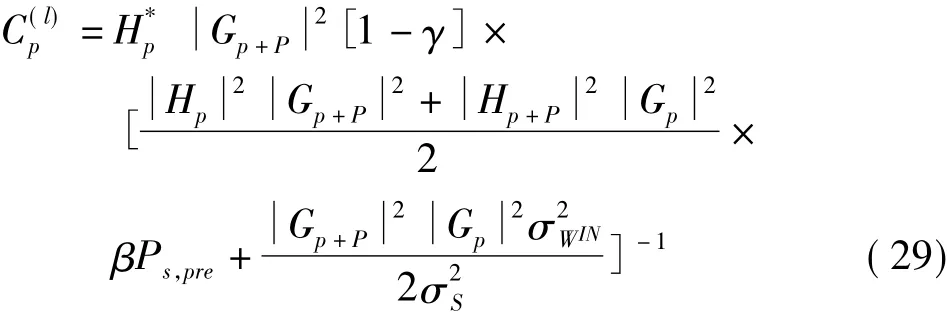
式中，Gp，Hp是周期为 2P 序列，即 Gp－P=Gp+P，Hp－P=Hp+P，p=P，P+1，…2P －1。

至此，LC－IBDFE的抽头系数的设计和相关参数的简化估计全部完成。由式(28)、式(29)可以看出，LC－IBDFE抽头系数的计算与参数Ps，pre有关，下面本文将通过仿真的方法详细分析在Ps，pre取不同值的条件下LC－IBDFE性能的变化情况。此外本文还将比较LC－IBDFE和IBDFE的性能和复杂度，从而得出LC－IBDFE的性能与IBDFE相近。

3 仿真研究

本次仿真所用调制方式是QPSK。信道是加性高斯白噪声信道(AWGN)。设发送滤波器gT(t)、接收滤波器gR(t)为平方根升余弦滤波器，因此h(t)可以看成升余弦滤波器。升余弦滚降系数α=0．2;加速因子 ρ分别取 0．9、0．8。在接收端以 2/T的速率抽样后，系统得到序列{hi}，i=0，1，…Nh{gi}，i=0，1，…，Ng。设 Nh=Ng=81，L=40，分组长度P=256;最大迭代次数NI。对于IBDFE，其参数参数 r(l)S，^S、σ2^S的估计可以参考文献［11］。对于 LC－IBDFE，β=2。由参考文献［12］可得，SER 的门限值为 0．1。因此 Ps，pre≤0．1，通过数值搜索，本文可以得出当 Ps，pre=0．1 时，性能最优。

表1 显示了在 ρ=0．8、NI=3 的条件下，Ps，pre分别取 0．01、0．05、0．1、0．15、0．2 的 LC － IBDFE 性能的变化情况。通过图可以看出:①Ps，pre=0．1时LC－IBDFE的性能最优;②LC－IBDFE的性能对参数Ps，pre的小范围变化不敏感。

图4、图5分别显示了NI=2、3时LC－IBDFE和IBDFE的性能。由图中可以看出两种接收机在性能上很接近。此外，从图5也可以看出:当NI=3时，迭代次数对ρ=0．8的系统影响较大，而对ρ=0．9的系统影响较小。

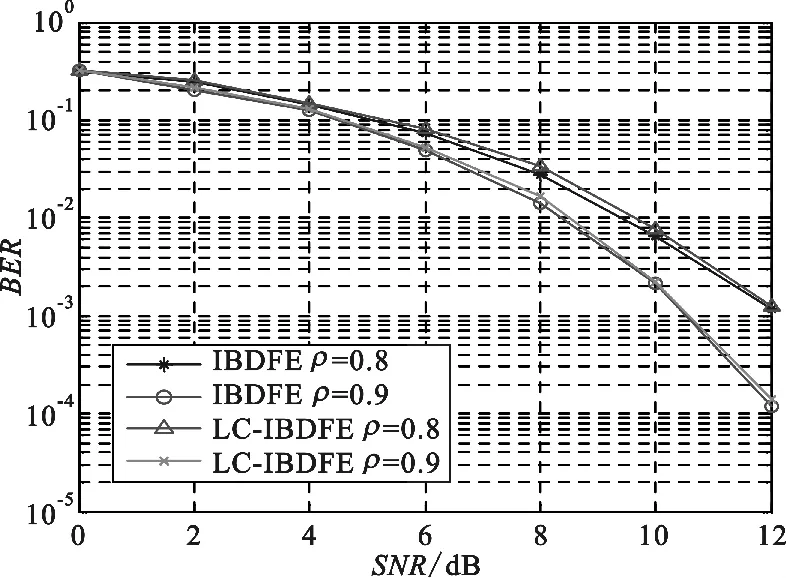
图4 2次迭代时LC－IBDFE和IBDFE的性能

图5 3次迭代时LC－IBDFE和IBDFE的性能

下面本文分析两种均衡器的复杂度。两种均衡器的复杂度计算主要来自4个部分，即:(1)DFT、IDFT计算;(2)DFE接收机处理信号所产生的计算;(3)抽头系数的计算式;(4)参数估计。对于IBDFE和LC－IBDFE，(1)、(2)两部分复杂度相同。其中DFT变换，这里采用FFT算法，其复数乘法数:P lb(2P)，复数加法数:2P lb(2P)。而DFE接收机处理信号时所产生的计算主要包括对信号的均衡操作、PN序列的注入和去除、2倍抽取和内插、信号判决等。

有所不同的是(3)、(4)两部分，下面本文从抽头系数的计算式和参数估计两个方面计算两种接收机的复杂度。为了降低复杂度的计算难度，在处理单个分组的信号时可以只计算一次，βPs，pre可以看成常数。

所以，IBDFE的判决出单个符号所需复数乘法数:

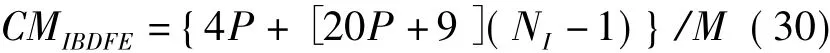
判决出单个符号所需复数加法数:

本文提出的LC－IBDFE判决出单个符号所需复数乘法数:

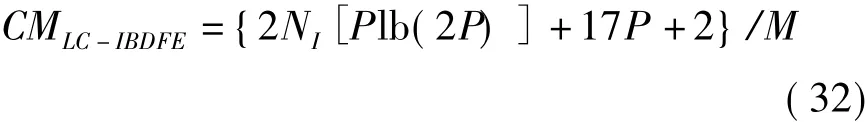
判决出单个符号所需复数加法数:

由式(32)、式(33)可以看，LC－IBDFE的前向、反向抽头系数每个信号分组只计算一次，不用随着迭代次数的增加而更新。因此，在高迭代次数的条件下，LC－IBDFE的复杂度优势将更明显。假设IBDFE 参数 r(l)S，^S、σ2^S估计过程里的系数 PS=2P，由式(30)～式(33)可以计算得出接收机复杂度与迭代次数的关系。图6是在P=256，L=40条件下，LC－IBDFE和IBDFE的复杂度与迭代次数的关系图。当NI=2时，LC－IBDFE判决单个符号所用复乘数比IBDFE降低约11．7%，复加数降低约7．1%;当NI=3时，LC－IBDFE判决单个符号所用复乘数比IBDFE降低约27．6%，复加数降低约12．3%。

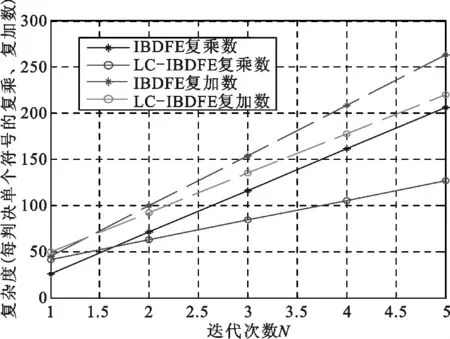
图6 均衡器复杂度与迭代次数的关系

4 结语

本文针对已有的IBDFE接收机存在的复杂度较高的问题提出了一种降低复杂度的新方法，从而提出了LC－IBDFE。LC－IBDFE同样遵循MMSE准则，通过将判决信号中的误差与期望信号分离，引入判决错误符号的方差，预定义符号错误率(SER)等方法简化了均衡器抽头系数的计算。因此对于每个信号分组，LC－IBDFE的前向、后向抽头系数只需计算一次，而不必像IBDFE那样抽头系数随着迭代次数的增加不断更新。从而有效降低了复杂度，实现性能与复杂度更好的折衷。仿真结果表明:在P=256，L=40条件下，当最大迭代次数NI=2时，LC－IBDFE判决单个符号所用复乘数比IBDFE降低约11．7%，复加数降低约7．1%;NI=3时，LCIBDFE判决单个符号所用复乘数比IBDFE降低约27．6%，复加数降低约12．3%。

下一步的主要工作可以从两个方面展开:首先，IBDFE接收机原本用于多径衰落信道，这将有利于未来LC－IBDFE和FTN理论向多径衰落信道中的推广，从而进一步向实用化发展;其次在降低接收端复杂度的同时也要兼顾性能，针对IBDFE和LCIBDFE，可以通过使用BCJR、turbo码等编码方法提高接收机的性能。

参考文献:

［1］ Mazo J E，Faster－ than － Nyquist Signaling［J］，Bell Syst．Tech J，1975，vol．54，issue．8:1451 －1462．

［2］ Anderson J B，Rusek F，Owall V，Faster than Nyquist Signaling［J］，Proc．Of IEEE，2013，vol．101，issue．8:1817－1830．

［3］ Liveris A D，Georghiades C N，Exploiting Faster－than－ Nyquist Signaling［J］，IEEE Trans．Commun．，2013，vol．51，issue．9:1502 －1511．

［4］ Sugiura S，Frequency － Domain Equalization of Faster than Nyquist Signaling［J］，IEEE Wireless Commun．Lett．，2013，vol．2，issue．5:555 －558．

［5］ Tomasin S，Benvenuto N，Fractionally Spaced Non－linear Equalization Qualization of Faster Than Nyouist Signals［C］//Signal Processing Conference(EUSIPCO)，Lisbon，Portugal，2014:1861 －1865．

［6］ Benvenuto N，Dinis R，Falconer D，et al．Single Carrier Modulation with Nonlinear Frequency Domain Equalization:An Idea Whose Time Has Come Again［J］，Proc．Of IEEE，2010，vol．98，issue．1:69 －96．

［7］ Salz J，Optimum Mean － Square Decision Feedback E-qualization［J］，Bell Syst．Tech．J．，1973，vol．52，issue．8:1341 －1373．

［8］ Benvenuto N，Tomasin S，On the Comparison Between OFDM and Single Carrier Modulation with a DFE using a Frequency Domain Feedforward Filter［J］，IEEE Trans．Commun．，2002，vol．50，issue．6:947 －955．

［9］ 张宝燕，葛万成．SC－FDE系统中频域均衡算法的改进［J］．通信技术，2010，43(06):83 －89．ZHANGBao－yan，GE Wan－cheng，Improvement on Frequency Domain Equalization Algorithm in SC－FDE System［J］，Communications Technology，2010，43(06):83 －89．

［10］ 吴世奇．一种基于STBC的SC－FDE系统双天线联合检测算法［J］．通信技术，2015，48(05):546－550．WU Shi－ qi．A Novel Joint Detection Algorithm of Dual－Antennas in STBC－SC－FDE System，Communications Technology，2015，48(05):546－550．

［11］ Tomasin S，Benvenuto N．Iterative Design and Detection of a DFE in the Frequency Domain［J］，IEEE Trans．Commun．，2005，vol．53，issue．11:1867 －1875．

［12］ ZHANGChao，WANGZhao－cheng，PAN Chang－yong，et al．Low －Complexity Iterative Frequency Domain Decision Feedback Equalization［J］，IEEE Trans．On Vehicular Technology，2011，vol．60，issue．3:1295 －1301．

［13］ vSainte－Agathe F，Sari H．New Results in Iterative Frequency－Domain Decision－Feedback Equalization［C］//Signal Processing Conference 14th European，Florence，Italy，2006:1 －4．

［14］ ZHANGChao，PANChang－yong．Low－Complexity Iterative Frequency Domain Decision Feedback Equalization［C］//Vehicular Technology Conference Fall(VTC 2010－Fall)of IEEE，Ottawa，Canada，2010:1 －5．