基于FAHP的服务型制造企业供应商的选择研究*

王　宇，尚　利，汪永超，赵建平

(四川大学 制造科学与工程学院，成都　610065)



基于FAHP的服务型制造企业供应商的选择研究*

王宇，尚利，汪永超，赵建平

(四川大学 制造科学与工程学院，成都610065)

服务型制造是一种制造和服务相互融合的先进制造模式，其具有整合、增值和创新等特点。为了提高竞争力，核心企业将非核心业务外包给其他企业。外包供应商的选择是一个多层次、多准则、多方案的决策问题，考虑到决策者决策的模糊性，提出一种基于三角模糊层次分析法的解决方案。从服务能力及质量、成本柔性、交货柔性、企业信誉、环保绩效、企业生产与技术能力六个方面建立指标评价体系，根据指标权重、指标值得分和可行性方案得分确定最优方案。最后通过一个实例，验证该方法的可行性。

服务型制造；供应商选择；三角模糊数；模糊层次分析法

0　引言

针对服务业与制造业不断融合的趋势，以西安交通大学汪应洛、孙林岩为代表的中国学者根据中国制造的现状与需求，提出了服务型制造模式[1-2]，服务型制造是制造与服务相融合的新产业形态，是新的先进制造模式。服务型制造是为了实现制造价值链中各利益相关者的价值增值，通过产品和服务的融合、客户全程参与、企业相互提供生产性服务和服务性生产，实现分散化制造资源的整合和各自核心竞争力的高度协同，达到高效创新的一种制造模式，是基于制造的服务和面向服务的制造。在服务型制造企业中，根据核心竞争理论，核心企业更加专注自己的核心竞争力，将非核心的业务外包给相应的其他企业，并与之建立稳定的战略联盟关系。供应商的选择直接影响到企业的生产和销售，同时对企业竞争力的创造和维持具有重要意义[3]。因此，选择合适的供应商显得尤为重要。

供应商的选择是一个多目标决策问题，需要对多个供应商在多个相互影响的准则基础上进行评价。国外学者Dickson在1966年通过分析170份对采购代理人和采购经理的调查结果，得到了23项供应商绩效评价标准。在Dickson基础上，1991年Weber统计了1966～1991年的74篇文章，重新评价了这23项评价指标在实际应用中的被关注程度，并对其重要程度进行了排序[4]。目前对供应商的选择研究主要集中在传统供应链、虚拟企业等企业网络，对于服务型制造企业供应商选择的研究较少。在评价方法上主要有层次分析法、模糊综合评价法、模糊相似优先比法等，这些方法存在评价结果受人为主观因素影响较大，从而影响最优结果选取的问题。因此本文提出应用模糊层次分析法对供应商进行选择。

模糊层次分析法(Fuzzy analysis hierarchy process, FAHP)是将模糊理论与传统的层次分析法相结合，充分考虑人思考的模糊性和主观性的一种理论方法[5]。本文针对各项指标，结合三角模糊数理论和层次分析法，通过建立模糊层次结构模型和模糊判断矩阵，确定各指标权重值。

1　评价指标体系的建立

针对某一任务，在满足核心企业要求的条件下，可供选择的供应商有很多。因此，在进行供应商选择的时候要综合考虑多个决策因素，然后对各种可选的供应商进行对比，评价和决策，得出最佳的供应商，使核心企业的利润最大。

对于供应商选择这个多层次、多目标的优化选择问题，首先要建立一套可行的决策目标评价体系。由文献[6]知服务型制造企业选择供应商的新标准为环保绩效、服务能力及质量、成本柔性，其中服务能力及质量是供应商能否被选中的关键因素。在全面性、简洁性、科学性、稳定可比性和灵活可操作性的原则指导下，结合文献[3，5]相关分析，建立服务型制造企业供应商选择评价指标体系，如图1所示。由于各评价指标自身又包括影响因素子集，所以还可以继续划分[7]。比如服务能力及质量指标包括信息化程度、客户响应度、一致性等。

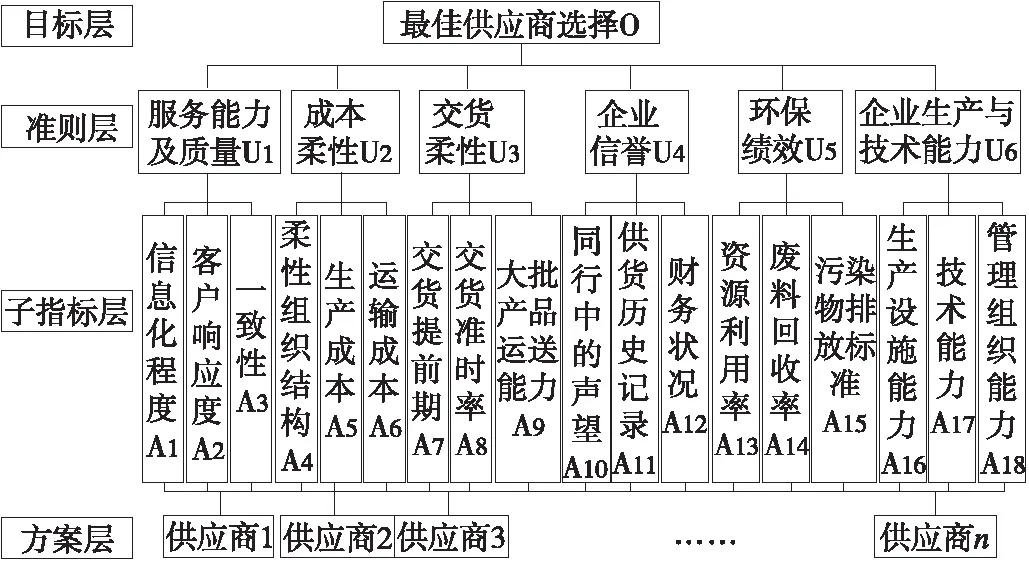
图1　供应商指标评价体系

2　三角模糊层次分析法

2.1三角模糊数

定义1：设实数集R上的一个模糊数M，当M的隶属度函数μM：R→[0,1]满足下列式(1)时，称其为一个三角模糊数[8～10]。

(1)

根据式(1)，一个模糊数M(l，m，u)的关系函数如图2所示。

图中l≤m≤u，l和u表示M的下界和上界值。m为M的隶属度为1的值。

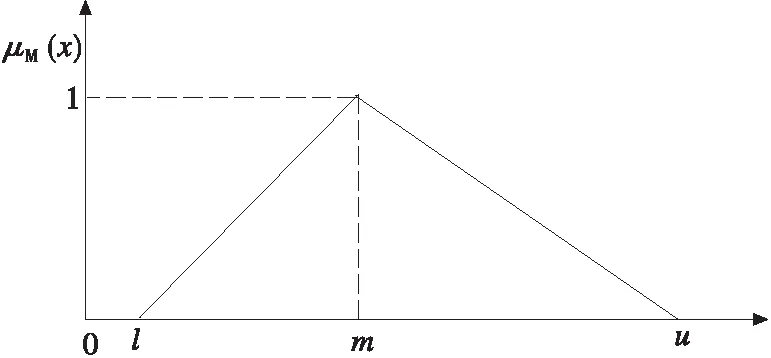
图2　三角模糊数M及其关系函数

在指标评价的两两比较矩阵中，为了考虑人的模糊性，三角模糊数被用来代表传统的具体数值，如表1所示。

表1　三角模糊数比较

定义2：两个三角模糊数M1和M2的运算法则：

M1=(l1,m1,u1);M2=(l2,m2,u2)

M1+M2=(l1+l2,m1+m2,u1+u2)

M1⊗M2=(l1×l2,m1×m2,u1×u2)

M1φM2=(l1/l2,m1/m2,u1/u2)

定义3：M1(l1,m1,u1)和M2(l2,m2,u2)是三角模糊数。M1>M2的可能度用三角模糊函数定义为：

(2)

其中d是M1与M2的交点如图3所示。

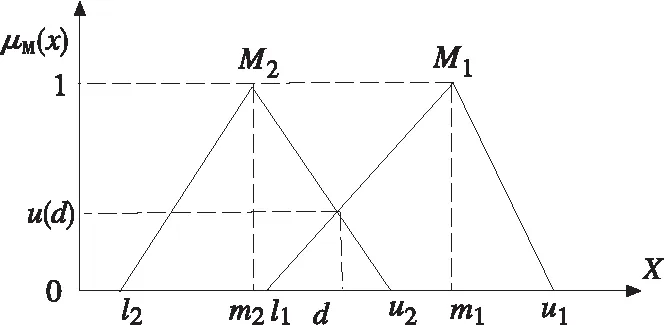
图3　M1与M2的交点

定义4：一个模糊数大于其它K模糊数的可能度被定义为：

(3)

2.2模糊判断矩阵的建立

模糊层次分析法的关键在于建立判断矩阵，所建立的判断矩阵是否科学、合理，直接影响到模糊层次分析法的效果[11]。通过对各因素的重要程度两两进行相比较构成一个判断矩阵。通过相互比较确定各指标相对其它指标的重要性，构建模糊判断矩阵R=(aij)n×n如下：

HsE1E2…EnE1a11=(1,1,1)a12=(l12,m12,u12)…a1n=(l1n,m1n,u1n)E2a21=(l21,m21,u21)a22=(1,1,1)…a2n=(l2n,m2n,u2n)……………Enan1=(ln1,mn1,un1)an2=(ln2,mn2,un2)…ann=(1,1,1)

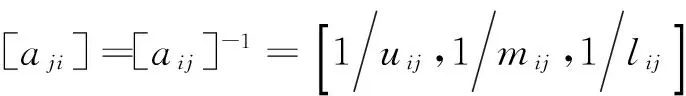
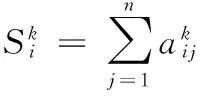
(4)

(5)

(6)

2.4层次单排序

层次单排序是指，对于上一层某个指标而言，本层次各指标的重要性的排序。

(7)

(8)

W(K)=(W1,W2,…,Wn)

(9)

其中Wi为指标Ei的权重。

2.5层次总排序

层次总排序是针对目标层而言，本层次各要素重要程度的依次排列。假设层次结构由k个层次(目标层为第一层)，则层次总权重为：

(10)

2.6各方案中的子指标值得分的确定

构建模糊判断矩阵时，以不同方案的同一子指标值为比较对象，比较相对优劣程度[12]。其它步骤与目标权重确定的步骤相同，以计算出的权重值为子指标值的得分，得到子指标值得分矩阵G(见表2)。

表2　子指标得分矩阵

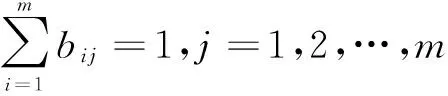
2.7各方案得分确定

F为各方案得分，依据计算结果选择得分最高的供应商方案ft。

F=100·W·GT=(f1,f2,…,fm)

ft=maxfj,j=1,2,…,m

(11)

3　案例分析

某核心制造企业需要一批齿轮零件，齿轮的基本参数：齿形-圆柱直齿轮；材料45#；模数4；齿数38；外径φ160；切齿宽度24；精度等级6-6-7(GB10095-88)。欲外包给某一企业做，现有4家可供选择的供应商企业。

3.1确定层次总权重

根据供应商选择模型层次结构中的各项指标，请三位专家按照定义的模糊数分别对准则层进行模糊评估给出三角模糊值，如表3所示。

将三位专家得到的模糊值加权平均得到的三角模糊判断矩阵如表4所示。

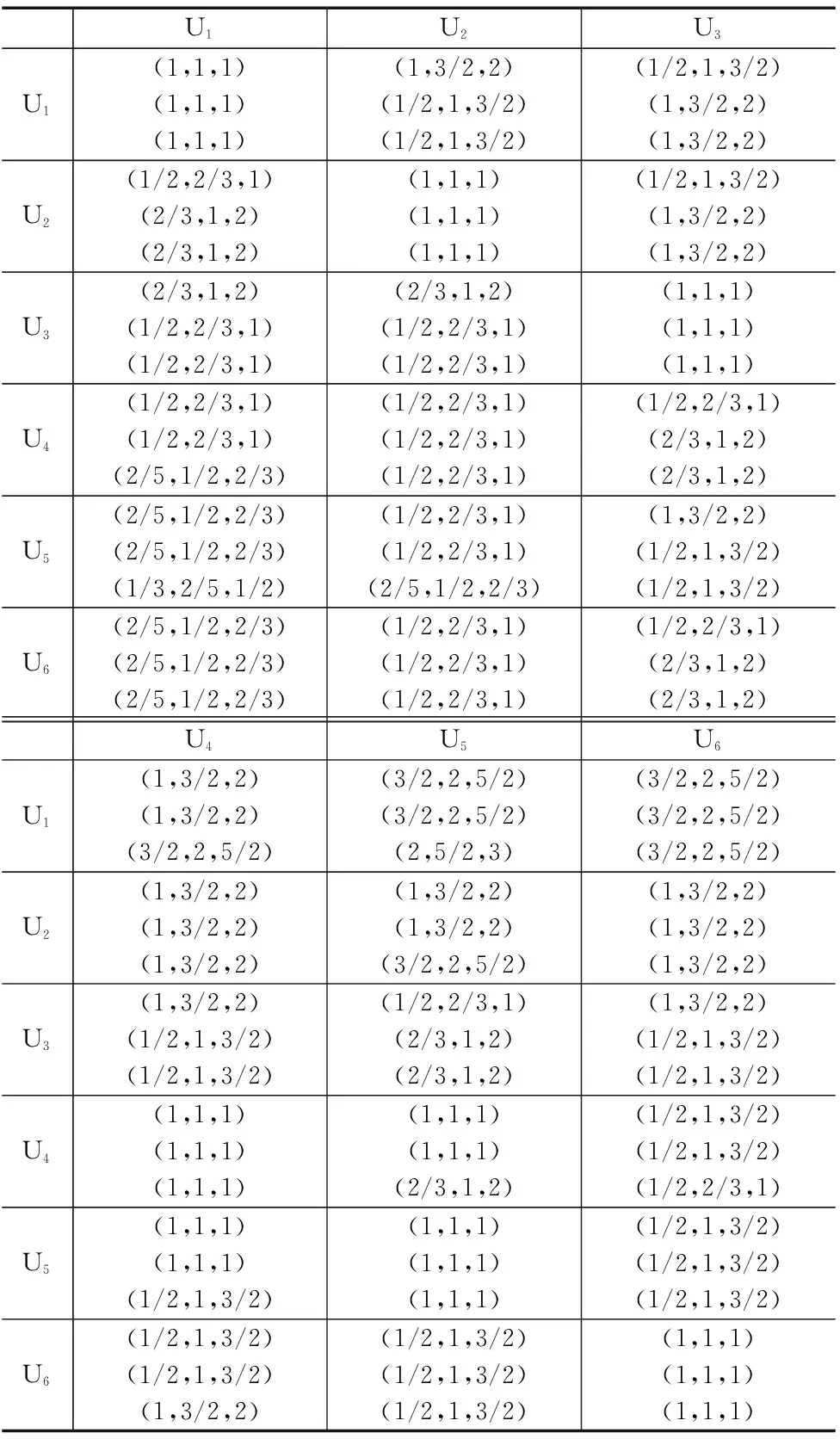
表3　准则层三角模糊数

表4　指标层三角模糊判断矩阵

由公式(4)、(5)、(6)可得准则层各指标的初始权重值如下：

SU1=(0.132，0.244，0.405)

SU2=(0.109，0.207，0.381)

SU3=(0.078，0.146，0.298)

SU4=(0.077，0.132，0.258)

SU5=(0.074，0.137，0.244)

SU6=(0.071，0.134，0.262)

由公式(2)、(7)将模糊值变为一般的值

d(SU1)=V(SU1≥SU2, SU3, SU4, SU5, SU6)=

min(1,1,1,1,1)=1

d(SU2)=V(SU2≥SU1, SU3, SU4, SU5, SU6)=

min(0.868,1,1,1,1)=0.868

d(SU3)=V(SU3≥SU1, SU2, SU4, SU5, SU6)=

min(0.626,0.756,1,1,1)=0.626

d(SU4)=V(SU4≥SU1, SU2, SU3, SU5, SU6)=

min(0.529,0.668,0.932,0.974,0.992)=0.529

d(SU5)=V(SU5≥SU1, SU2, SU3, SU4, SU6)=

min(0.511,0.662,0.953,1,1)=0.511

d(SU6)=V(SU6≥SU1, SU2, SU3, SU4, SU5)=

min(0.540,0.679,0.940,1,0.982)=0.540

由公式(8)、(9)将权重值标准化，得到指标最终权重

W2=(0.245,0.213,0.154,0.130,0.126,0.134)

故在供应商的选择中,服务能力及质量、成本柔性、交货柔性、企业信誉、环保绩效、企业生产与技术能力指标权重值分别为0.245、0.213、0.154、0.130、0.126、0.134。

采用同样的方法可得子指标层权重，由公式(10)可得层次总权重，如表5所示。

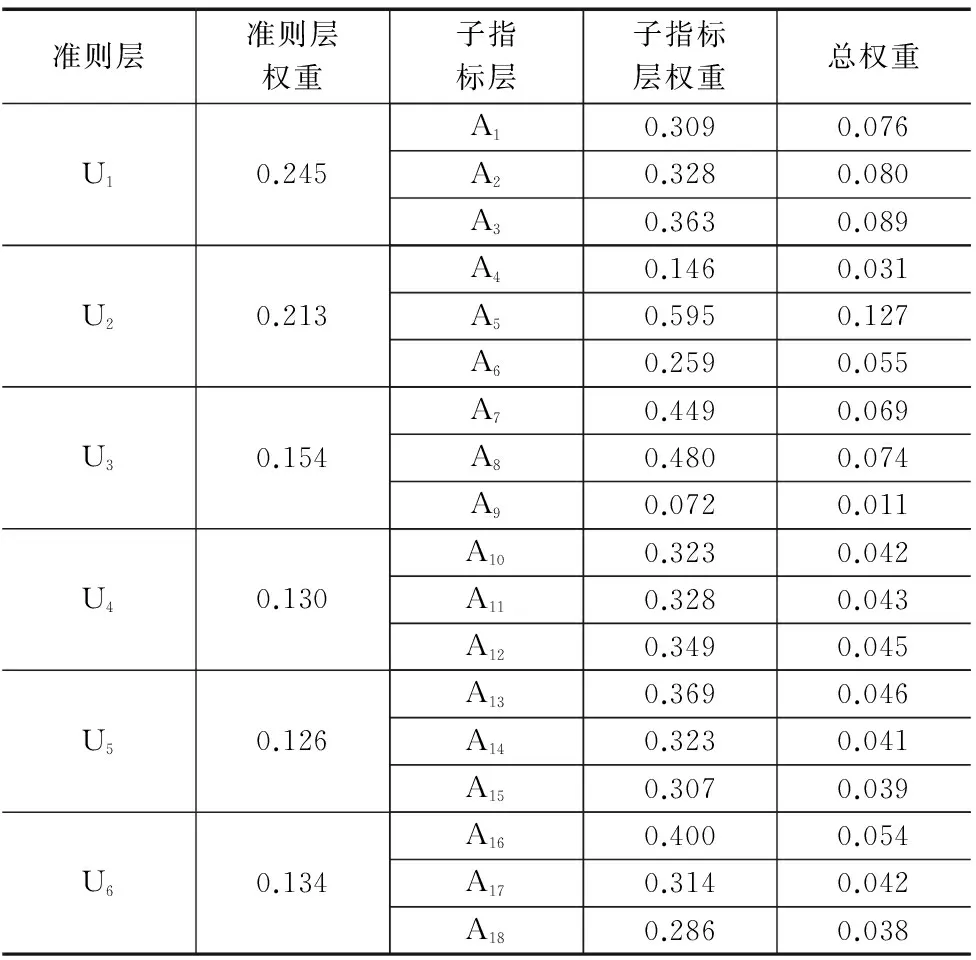
表5　子指标权重

W=(0.076，0.080，0.089，0.031，0.127，0.055，0.069，0.074，0.011，0.042，0.043，0.045，0.046，0.041，0.039，0.054，0.042，0.038)

3.2确定各子指标值得分

采用三角模糊层次分析法确定各子指标值的得分，可以有效的减小时间、人力、物力成本。三位专家依据经验对可供选择的4家供应商(P1，P2，P3，P4)的各指标值进行模糊评估，给出三角模糊值，由公式(4)、(5)、(6)、(7)、(8)、(9)可得各子指标得分如表6所示。

表6　子指标得分

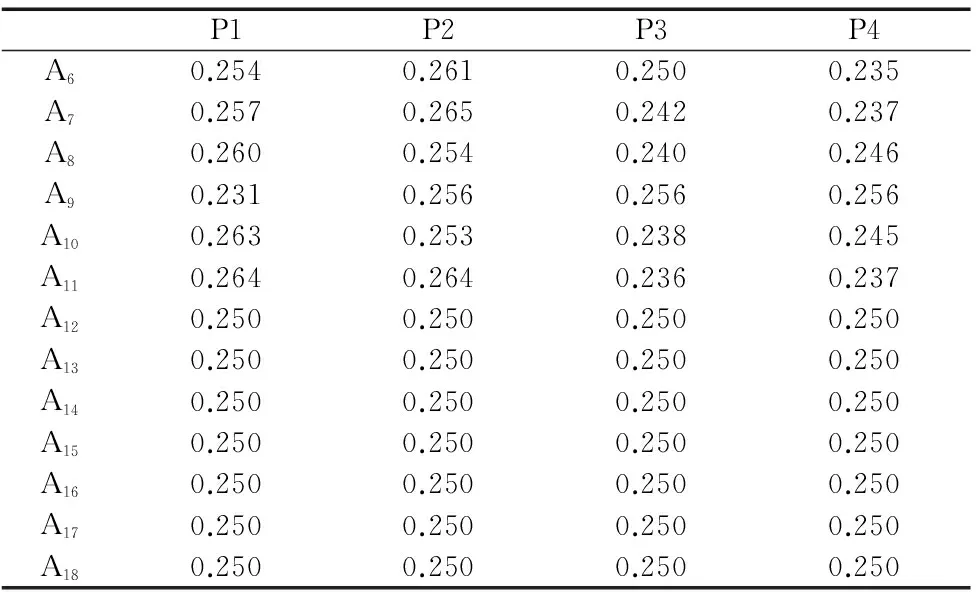
续表

3.3计算各方案得分

由公式(11)可得F=(25.47，25.76，24.51，24.47)。由得分向量可知供应商2为最佳供应商。

4　结论

服务型制造模式中，核心企业为提高核心竞争力，将非核心业务外包给其他供应商企业。本文借鉴国内外研究成果建立了由服务能力及质量、成本柔性、交货柔性、企业信誉、环保绩效、企业生产与技术能力6个一级指标和生产中的质量等18个二级指标组成的供应商指标评价体系，该指标评价体系较全面地反映了供应商选择的主要因素，为企业提供了评价依据。

模糊层次分析法考虑到决策者决策的模糊性使选择结果更加合理，且该方法易于计算机编程实现，具有很大的实用性。本文利用三角模糊数来表达专家的评判值，构建模糊判断矩阵，最后利用模糊层次分析法确定最佳供应商。

[1] 孙林岩，李刚，江志斌，等.21世纪的先进制造模式-服务型制造[J].中国机械工程，2007，18(19)：2307-2312.

[2] 孙林岩，高杰，朱春燕，等.服务型制造：新型的产品模式与制造范式[J].中国机械工程，2008，19(21):2600-2688.

[3] 陆乃方，尤建新，黄志明.生产性服务外包供应商选择的关键要素分析[J].经济研究导刊，2009(36):165-168，178.[4] 刘晓，李海越，王成恩，等.供应商选择模型与方法综述[J].中国管理科学，2004,12(1)：139-148.

[5] 王化吉，宗长富，管欣，等.基于模糊层次分析法的汽车操作稳定性主观评价指标权重确定方法[J].机械工程学报，2011，47(24)：83-90.

[6] 王凌，孙林岩，冯泰文.服务型制造企业供应商选择研究[J].商业研究，2010(2)：1-5.[7] 王桂萍，贾亚洲，周文广.基于模糊可拓层次分析法的数控机床绿色度评价方法及应用[J].机械工程学报，2010，46(3)：141-147.

[8] 赵建平，王永超，殷国富，等.基于模糊层次分析法的切削液选择[J].组合机床与自动化加工技术，2014(7):19-22.

[9] Hossein Safari ，Alireza Faghih， Mohammad Reza Fathi. Integration of graph theory and matrix approach with fuzzy AHP for equipment selection[J]. Journal of Industrial Engineering and Management，2013，6(2):477-494.

[10] Mohammad T Issai，Aram Kanani，et al.Intelligent timetable evaluation using fuzzy AHP[J].Expert Systems with Application, 2011,38:3718-3723.

[11] 张吉军.模糊层次分析法(FAHP)[J].模糊系统与数学,2000，14(2)：84-89.

[12] 陈欣.模糊层次分析法在方案优选方面的应用[J].计算机工程与设计，2004，25(10)：1847-1849.

(编辑李秀敏)

Study on Vendor Selection in Service-oriented Manufacturing Based on FAHP

WANG Yu，SHANG Li，WANG Yong-chao，ZHAO Jian-ping

(School of Manufacturing Science and Engineering, Sichuan University, Chengdu 610065, China)

The service-oriented manufacturing, an advanced manufacturing mode integrated with both manufacturing and service, has the characteristics of integration, value increment, innovation and so on. In order to improve competitiveness, core enterprises outsource non-core business to other enterprises. Outsourcing vendor selection is a multi-level, multi-criteria and multi-solution decision-making problem. Considered the fuzziness of decision-making, a solution based on triangular fuzzy hierarchy analysis is put forward. From six aspects as service ability and quality, flexibility of cost, flexibility of delivery, enterprise credit, environmental performance, enterprise production and technical capabilities, the index evaluation system is established. And the optimal solution is determined according to the index weights, index score and alternative solutions. Finally, a case study is given to validate the feasibility of this method.

service-oriented manufacturing; vendor selection; triangle fuzzy number; fuzzy analytic hierarchy process

1001-2265(2015)11-0145-04DOI:10.13462/j.cnki.mmtamt.2015.11.040

2015-01-14；

2015-01-27

周光源(1990—)，男，安徽安庆人，合肥工业大学硕士研究生，研究方向为制造过程监测与控制，(E-mail)zhougy1990@126.com。

TH18;TG506

A