基于齿形折算法的椭圆齿轮参数化建模及运动仿真研究

史　诺,刘　琼,冯东旭,鲁剑啸

(1.杨凌职业技术学院 a.机电工程分院；b.信息工程分院,陕西 杨凌　712100；2.延安大学 化学与化工学院，陕西 延安　716000)



基于齿形折算法的椭圆齿轮参数化建模及运动仿真研究

史诺1a,刘琼1b,冯东旭1a,鲁剑啸2

(1.杨凌职业技术学院 a.机电工程分院；b.信息工程分院,陕西 杨凌712100；2.延安大学 化学与化工学院，陕西 延安716000)

椭圆齿轮是一种典型的非圆齿轮，具有非均匀、周期性变化的传动比特性，在机床、轻工自动机械、仪器仪表等诸多领域中取得了良好的应用效果。椭圆齿轮的建模研究对于其推广应用具有重要意义。根据椭圆齿轮的结构特点，采用齿形折算法的原理，基于CREO进行了参数化建模，并以此为基础在ADAMS中构建了运动仿真模型，仿真结果表明椭圆齿轮副啮合传动情况与理论分析保持一致，证明了建模方法的可行性，为椭圆齿轮的数控加工提供了基础的技术依据。

齿形折算法；椭圆齿轮；参数化建模

0　引言

椭圆齿轮是一种典型的非圆齿轮，集成了圆形齿轮和凸轮的结构特点，可实现精确的非均匀周期性传动。在自动机床的转位机构、插齿机的主运动机构、高速印刷机中的输纸机构、纸板机中的切刀机构中椭圆齿轮都取得了良好的应用效果[1-4]，但是从工程实际情况来看，较大的加工难度制约了椭圆齿轮的普及应用。随着CAD/CAM技术及数控技术的快速发展，解决椭圆齿轮的建模问题就会突破制造中的障碍，因此建模研究具有重要意义。现有文献提出的建模方法存在的问题是设置了特定参数，没有实现系列化、变异化的精确设计，有一定的局限性[5-6]。鉴于此，根据椭圆齿轮的传动特性及齿廓特点提出了基于齿形折算法的参数化建模方法，并利用运动仿真验证了该方法的正确性。本文提出的参数化建模方法可大大缩短设计与制造周期，对于椭圆齿轮的推广应用具有一定价值。

1　建模思路

图1　齿形折算法的原理

椭圆齿轮的建模可采用解析法进行，通过求解齿廓曲线的解析方程得到齿廓上的点，然后插入直线或圆弧进行拟合，为了得到精确的齿廓，就需要计算出足够多的点，导致建模过程过于繁琐。另外一种建模思路是将椭圆齿轮的每一个齿折算成当量圆齿轮的齿形，这种方法称为齿形折算法。齿形折算法的基本原理是以节曲线上每一个轮齿中心所对应的曲率中心及曲率半径为基准做分度圆，以此为基础生成圆齿轮的齿形，这样椭圆齿轮就可看做是在每个轮齿中心一个插入模数相同，但分度圆直径不相等的等效圆齿轮的轮齿构成的[7]。如图1所示，1点是椭圆齿轮某齿弧厚的中点，这个齿的齿形对应于圆心为O1、分度圆半径为r1的相同模数的圆柱齿轮的齿形，对于2点，此处的齿形对应于圆心为O2、分度圆半径为r2的圆柱齿轮的齿形。齿形折算法无需大量计算，得到的齿形的精确度可满足大部分实际应用场合的需求，是一种切实可行的建模方法。

2　参数化建模

CREO是当今世界上最成功的CAD/CAM软件之一，应用较为广泛。利用齿形折算法在CREO软件平台上对椭圆齿轮进行参数化设计，可以方便的更改参数值实现模型的更新设计，大幅度提高了工作效率。

2.1驱动参数的确定

一对椭圆齿轮的节曲线是相互啮合的一对椭圆齿轮在传动过程中实现无滑动的滚动共轭曲线，如图2所示。从几何关系上讲节曲线、齿根曲线、齿顶曲线在法向上是等距线，故节曲线的参数对于椭圆齿轮起着非常重要的作用。

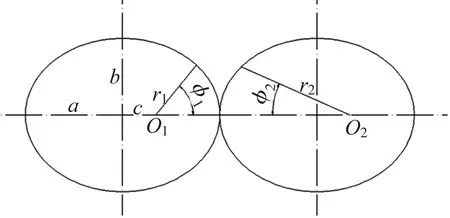
图2　椭圆齿轮的节曲线

椭圆齿轮的节曲线方程为：

由此方程可以得出长轴半径a与偏心率e决定着节曲线的形状。

椭圆齿轮的传动比为：

由传动比方程中可以得出节曲线的偏心率e决定着传动比变化曲线。一般情况下，进行齿轮传动结构的设计时必须根据实际工况选取合适的传动比，所以偏心率e是首先需要确定的参数。

由图7得知，对照组干腌羊火腿的肌原纤维蛋白发生了降解，但降解程度不大。分子量为63.0 ku～48.0 ku和48.0 ku～35.0 ku中间出现蛋白条带逐渐变粗；35.0 ku～25.0 ku中间出现了很多小的蛋白条带；25.0 ku～20.0 ku、20.0 ku～17.0 ku和17.0 ku～11.0 ku中间产生的蛋白条带逐渐变粗，颜色也逐渐加深，说明高分子蛋白降解产生了新的蛋白片段。

椭圆齿轮的特点是轮齿在节曲线上均匀分布，模数m、齿数z与节曲线的周长L的关系为：

L=πmz

综和上述各种因素，选取椭圆齿轮节曲线的偏心率e与长轴半径a、模数m、齿数z作为驱动参数，通过这四个参数控制节曲线的的轮廓。这四个参数的具体数值需进行反复计算才能得出，谢漱峰详细计算与论证了椭圆齿轮传动及节曲线的计算[8]，模数m、齿数z、长轴半径a、偏心率e之间的关系为：

……)

2.2齿形的确定

椭圆齿轮的齿顶曲线、齿根曲线的确定方法与圆齿轮相同，都是将节曲线向上偏移一个齿顶高、向下偏移一个齿根高形成的。关键的步骤是确定轮齿左右两侧的齿廓曲线，为了实现良好的互换性，椭圆齿轮可采用与圆齿轮一样的标准齿条型刀具或插齿刀进行加工，因此选用标准渐开线作为椭圆齿轮的齿廓曲线[9-10]。

2.2.1轮齿位置的确定

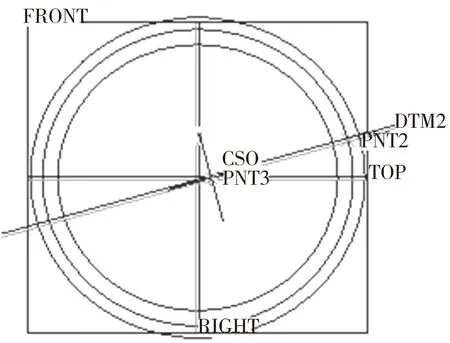
图3　轮齿位置图

确定了轮齿中心及其所对应的曲率中心，轮齿才能够精准定位。各轮齿的中心点在节曲线上均匀分布，因此以节曲线作为参照，按照比率的方式确定。如图3所示，当定义比率为2/z时，生成基准点PNT2,此点即为第2齿的轮齿中心。创建通过PNT2点且垂直于节曲线的基准面DTM2，再创建通过FRONT面与TOP面的基准轴A-2，基准面与基准轴的交点PNT3即为PNT2点所对应的曲率中心。

由椭圆齿轮的节曲线方程可以得到各轮齿的中心点所对应的曲率半径为：

标记PNT2点与PNT3点之间的距离，此距离为曲率半径，即当量齿轮的分度圆半径，将此距离赋值给R2，并计算出相应的基圆半径。以曲率中心PNT3为原点创建坐标系CS0，在此坐标系下构建轮齿2的齿廓曲线。

在CS0坐标系下通过方程定义渐开线，由于PNT2点是第二个轮齿的中心点，所以生成的渐开线并不是齿廓右侧的曲线，需要将其绕当量齿轮的圆心PNT3旋转。郭利对旋转的角度应用简图演示和数学推导的方法进行了研究，对于压力角为20°的标准齿条型刀具或插齿刀而言，旋转的角度为90m/R2+0.853945[11]。旋转后得到的曲线以DTM2面为镜像平面，得到左侧的齿廓曲线，如图4所示。齿根过渡圆弧的绘制利用倒圆角命令完成，其半径为0.38m，绘制完成的轮齿2齿形如图5所示。

由于节曲线上各轮齿中心曲率半径不同，故各个轮齿的齿廓曲线也并不相同，采用上述相同的步骤设计其余各轮齿齿廓，将长轴上半部分的齿廓形状绘制完毕后进行镜像，对各轮齿及齿根圆进行拉伸操作，随后创建轴孔、键槽，完成椭圆齿轮的整体造型。

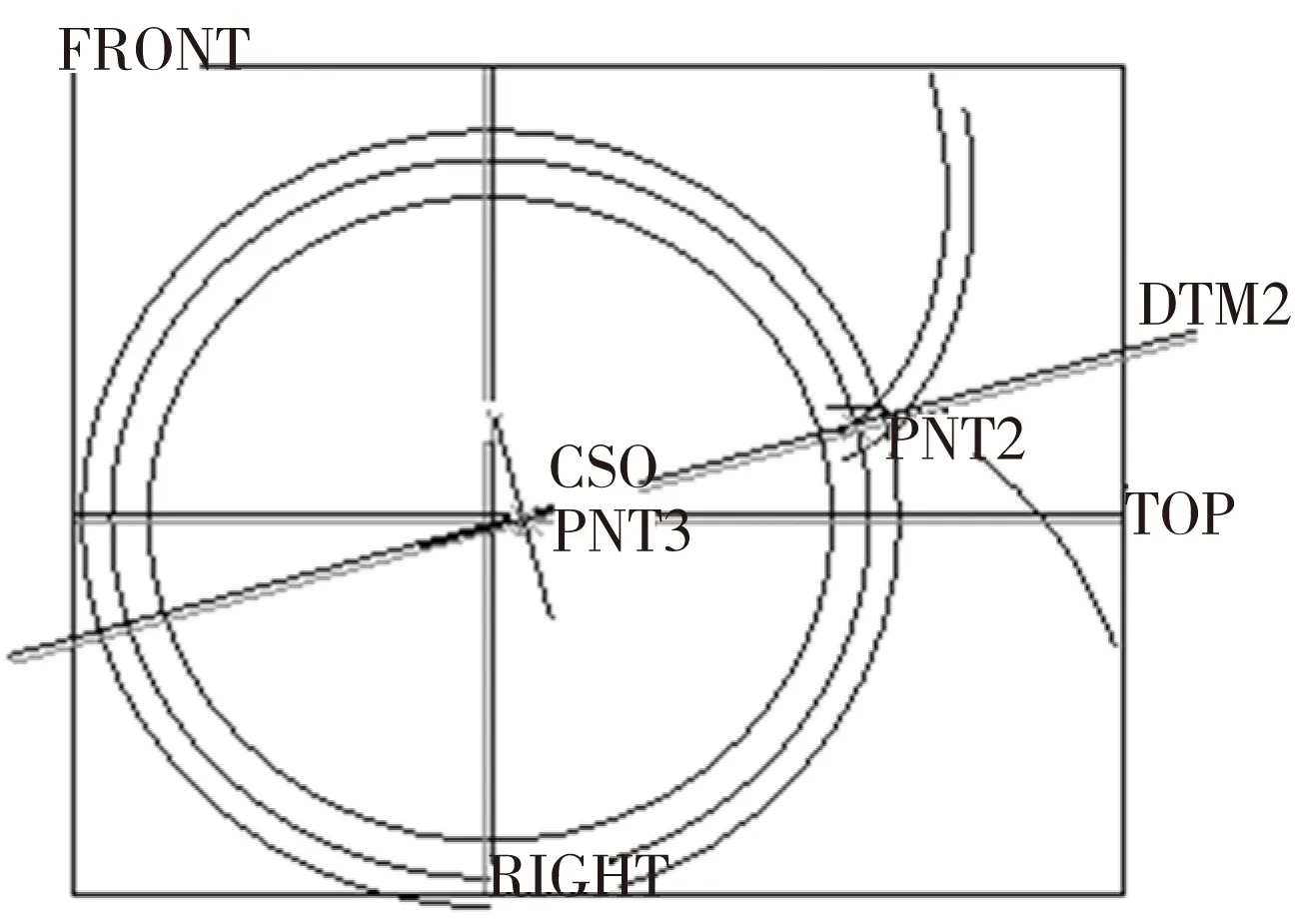
图4　渐开线的旋转及镜像

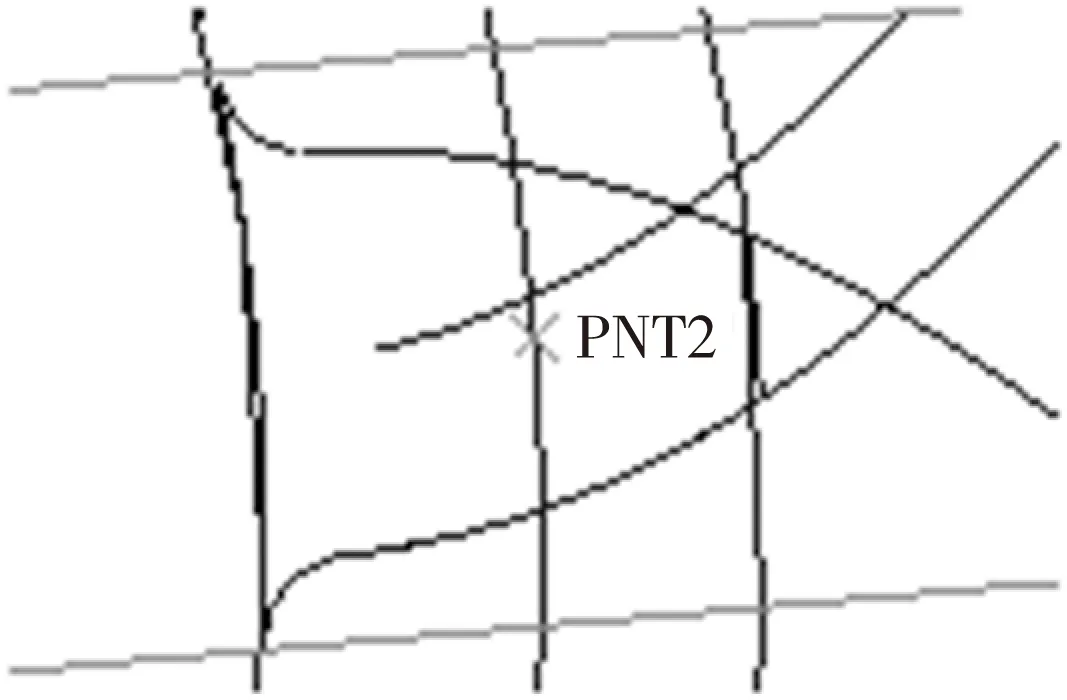
图5　齿形轮廓

2.3程序设计

在CREO软件中的程序编辑窗口中可以显示出系统自动生成的参数化设计程序，在INPUT和END INPUT中添加下列语句。

INPUT

E NUMBER

“请输入齿轮的偏心率 = =”

A NUMBER

“请输入齿轮的长轴 = =”

图6　椭圆齿轮三维模型

Z NUMBER

“请输入齿轮的齿数 = =”

M NUMBER

“请输入齿轮的模数 = =”

END INPUT

分别输入E=0.3，A=38.378667，M=3，Z=25，得到的三维模型如图6所示。

3　椭圆齿轮副的运动仿真

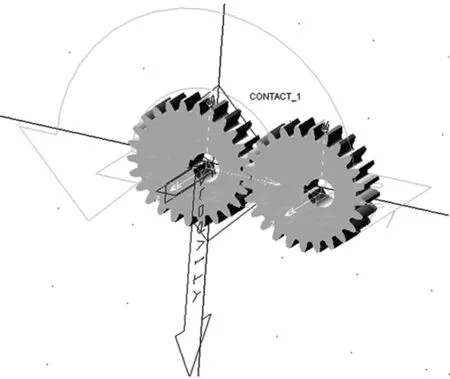
图7　椭圆齿轮副运动学分析模型

在CREO的组件模式下将椭圆齿轮进行装配，但是该软件的机构分析模块中只提供定传动比的齿轮副，因此将装配文件导入动力学分析软件ADAMS中进行分析。在两齿轮的中心轴与大地之间添加旋转副，创建驱动为120r/min，两齿轮之间施加接触力，保证主动轮能够推动从动轮转动，运动学分析模型如图7所示。

对模型的自由度进行验证，不存在冗余自由度，因而不需要重新修正模型。设置仿真时间为3s，运算步数为300步，计算结束之后进入ADAMS/Postprocessor中查看仿真结果。如图8所示，主动轮的角速度为水平直线，从动轮的角速度曲线存在一定的波动，一方面是由于定义了接触力，在传动中会产生振动[12]，另一方面是由于椭圆齿轮的变速特性形成了振动脉冲[13]。对比传动比公式可以看出，仿真曲线的变化趋势与理论分析保持一致，证明了椭圆齿轮模型的可行性。

图8　角速度仿真曲线

4　结束语

(1)利用齿形折算法进行椭圆齿轮参数化造型的原理直观明确，无需大量理论推导与计算，生成的实体模型可直接用于生成NC代码，能够为椭圆齿轮的数控加工提供基础的技术依据。

(2)利用动力学分析软件ADAMS对椭圆齿轮传动过程进行了分析，与理论上椭圆齿轮副啮合传动的情况相符，证明了利用齿形折算法设计的椭圆齿轮在精度上可满足实际工况的需求。

(3)本文采用的方法同样适用于其他非圆齿轮的造型与运动仿真，为非圆齿轮的设计提供了简洁、高效的途径。

[1] 王超.基于非圆齿轮的变速机构设计[D].北京:北京邮电大学,2010.

[2] 鲁彬.基于非圆齿轮传动的插齿机主运动机构的设计及研究[D].武汉:华中科技大学,2009.

[3] 张晓玲,沈韶华.实现变速输纸功能的椭圆齿轮优化设计[J].机械设计与研究,2004,20(2): 38-39.

[4] 李福生.非圆齿轮 [M].北京:机械工业出版社, 1975.

[5] 赵鑫,王惠源.椭圆齿轮三维建模与运动仿真分析[J].煤矿机械,2012,33(11): 67-68.

[6] Mundo D. Geometric design of a planetary gear train with non-circular gears [J]. Mechanism and Machine Theory,2006,41: 456-472.

[7] 周永清,朱思洪.使用CAXA与Pro/E的渐开线椭圆齿轮三维建模与运动仿真[J].工程图学学报,2009(3): 207-211.

[8] 谢漱峰.椭园和卵形齿轮传动及其节曲线计算[J].安徽工学院学报,1984(1): 14-23.

[9] 贾松,胡青春.基于CAXA的非圆齿轮的三维造型与设计[J].机械传动,2005,29 (1): 30-32.

[10] 武传宇,金玉珍,贺磊盈.基于包络特征的非圆齿轮齿廓计算方法研究[J].中国机械工程,2008,19(15): 1796-1799.

[11] 郭利.基于Pro/E的齿轮渐开线镜像问题新研究[J].机械工程师,2010(12): 66-67.

[12] 赵凤芹,张布,于文翠.基于ADAMS的椭圆齿轮传动运动学分析[J].新技术新工艺,2008(6):30-32.

[13] 杨存.非圆齿轮运动学与动力学研究[D].兰州:兰州理工大学,2014.

(编辑李秀敏)

Parametric Modeling and Motion Simulation Based on Tooth Profile Conversion Method of Elliptic Gear

SHI Nuo1a, LIU Qiong1b, FENG Dong-xu1a, LU Jian-xiao2

(1a.College of Mechanical & Electrical Engineering;b.College of Information Engineering, Yangling Vocational & Technical College, Yangling Shaanxi 712100,China;2.College of Chemical Engineering, Yan′an University, Yan′an Shaanxi 716000,China)

Elliptic gear is a typical non circular gear, with transmission ratio characteristics of heterogeneity and periodic variations, bringing excellent effects in practice such as machines, light industrial automatic machinery, instrumentation and other fields. The study on its modeling has an important significance for its popularization and application. According to the structural characteristics of elliptic gear and tooth profile conversion method, parametric modeling was carried out based on CREO, and motion simulation was constructed in ADAMS. The simulation results show that elliptic gear pair meshing transmission case is the same as theory analysis. This proves the feasibility of the modeling method, and provides the technical basis for the numerical control machining of elliptic gear.

tooth profile conversion method; elliptic gear; parametric modeling

1001-2265(2015)11-0114-03DOI:10.13462/j.cnki.mmtamt.2015.11.032

2014-12-23；

2015-01-27

史诺(1985—)，男，陕西杨凌人，杨凌职业技术学院讲师，硕士，研究方向为机械制造与自动化，(E-mail)shinuo7241@sina.com。

TH132;TG506

A