用于轴心轨迹提纯的小波精细积分算法
2015-10-31曹永宁
曹永宁,杨 勇
(1.宁夏职业技术学院 工业工程系,银川 750021;2.瑞斯康达科技发展股份有限公司,北京 100085)
用于轴心轨迹提纯的小波精细积分算法
曹永宁1,杨勇2
(1.宁夏职业技术学院工业工程系,银川 750021;2.瑞斯康达科技发展股份有限公司,北京 100085)
转子轴心轨迹是分析转子故障原因的重要依据。实测的轴心轨迹由于存在噪声干扰需要经过提纯方能用于转子故障分析。针对最新提出的偏微分方程轴心轨迹提纯新方法,提出小波精细积分提纯算法。数值结果表明,小波精细积分法可有效滤除信号中的噪声,且消噪之后的信号畸变小,保证了滤波前后信号固有结构不变。
轴心轨迹;提纯;小波精细积分
0 引言
转子轴心轨迹是分析转子故障原因的重要依据[1-2]。一般来说,当轴心轨迹表现为重叠且长短轴长度接近的椭圆时,表明转子是正常的。如果该椭圆的长短轴长度差距过大,表明轴承间隙或刚度差异较大。如果转子不对中,轴心轨迹表现为月牙状、香蕉状或8字形;若转子和轴承产生摩擦,轴心轨迹图中会出现多处锯齿状尖角或小环。转子发生亚异步自激振动时,其轴心轨迹往往很不稳定,不仅形状及大小时刻在发生较大的变化,而且还会出现大圈套小圈的情况。
实测转子振动信号往往含有噪声,噪声的存在会导致轴心轨迹图表现为杂乱无章的状态,给转子故障分析带来障碍。因此,在对轴心轨迹图进行分析前需要进行提纯。常见的提纯技术包括小波变换法[3],数字形态学滤波[4]等,但这些方法一般都存在频带选择不明确,降噪畸变大,初相位影响严重等问题[5]。为克服以上问题,近年来提出了基于偏微分方程的轴心轨迹提纯技术[3,6],有效克服了上述问题。偏微分方程大多采用差分法进行求解,精度和效率都受到限制。本文将小波精细积分法引入偏微分方程的求解[7-9],进一步提高了轴心轨迹提纯的精度和效率,进而对轴心轨迹识别精度以及自动化提供了有效支持。
1轴心轨迹提纯的偏微分方程模型及其
小波数值解
1.1偏微分方程模型
用于轴心轨迹提纯的偏微分方程模型常采用如下热传导方程[3]:

(1)
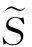
方程的解S就是滤波后的信号。显然,方程(1)的解和正常数c及方程的演化参数τ密切相关。尽管方程(1)是线性偏微分方程,但初始信号是带有噪声的振动信号,我们无法直接得到方程(1)的精确解析解。文献[3-4]给出了方程的差分法求解格式。由数值分析理论知识可知,差分法的稳定性与时间参数t和方程演化参数τ的离散网格大小相关。对于不同的振动信号,需要同时调试这两个参数方能得到收敛解。对工程技术人员提出了较高的要求,不利于该方法的应用推广。因此下面给出一种和偏微分方程演化参数无关的小波精细积分算法。
1.2小波精细积分算法
按照小波精细积分法的基本理论,u(x,t)可近似表示为:
(2)
式中wj(t-tn)是小波基函数的离散表达式,此处我们取如下Shannon-Gabor小波:
(3)
其中j∈z是小波尺度参数,r是小波的窗口大小参数,一般取3.2,ti是振动信号时间参数的离散表达,即
Shannon-Gabor小波(3)对应的一阶导数和二阶导数分别为:
(4)
(5)
将(2)~(5)式带入(1),则热传导方程(1)可被离散为如下微分方程组:
(6)
其中
(7)

(8)
微分方程组(6)的解析解为
(9)

H=exp(M·t)
由于该方法只在振动信号时域空间离散,热传导方程的演化时间空间采用了解析法求解,算法的稳定性只取决于振动信号时域空间离散网格的大小,从而大大提高了算法的稳定性和计算精度。
令Δt=t/2N(N为正整数),取
H=I+Hα=I+MΔt+(M·Δt)2×[I+(MΔt)/3+(MΔt)2/12]/2
表示exp(M·t)泰勒展开的前五项,则
H=[exp(M·Δt)]2N=(I+Hα)2(N-1)×(I+Hα)2(N-1)
这样的分解一直进行N次,便可精确得到H的值。将矩阵H代入迭代公式(9)可得到不同时间参数下偏微分方程(1)的数值解。
2 基于偏微分方程的轴心轨迹提纯
利用偏微分方程法对振动信号进行降噪,然后合成得到轴心轨迹图。为体现本文方法的优势,对差分法和小波精细积分法进行了对比。小波精细积分法中,尺度参数j=9,差分法离散点数为512。
图1是在传动试验台上测得的轴x,y方向振动实际数据,其中轴转速为750r/min,采样频率为4096Hz,其最大振动幅值为20μm。
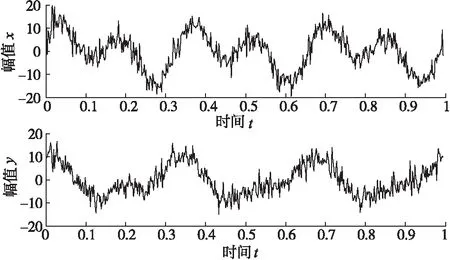
图1 带噪声振动信号
由带噪声振动信号直接得到的轴心轨迹图如图2所示。由于噪声的影响,轴心轨迹图显得杂乱无章,无法判断转子故障原因。

图2 带噪声轴心轨迹图
以X振动方向为例,图3和图4分别给出了差分法和小波精细积分法两种基于偏微分方程的信号降噪结果。

图3 差分法信号降噪结果

图4 小波精细积分法信号降噪结果
由于小波精细积分法的稳定性和时间步长无关,表中并未列出小波精细积分法的步长。对比图3和图4不难看出,在相同的时间参数下得到的振动信号滤波结果类似,但小波精细积分法得到的滤波结果更光滑一些。由于模型相同,降噪有效性相同,但小波精细积分法的精度更高一些,数值解的衰减更小。事实上,随着时间参数的不断加大,差分法同样可以得到更为光滑的结果。图5所示轴心轨迹图反映了差分法和小波精细积分法的精度。事实上,小波精细积分法是一种半解析法,不存在解误差的叠加问题,求解精度更高。图5也反映了这点。

图5 降噪后的轴心轨迹图
3 结束语
针对已有轴心轨迹提纯算法存在的问题, 给出了轴心轨迹提纯偏微分方程模型的小波精细积分算法。相对于差分法,小波精细积分法是一种半解析方法,该方法结合了小波多尺度方法和精细积分法的双重优点。在求解轴心轨迹提纯偏微分方程模型时,具有绝对稳定性,时间步长不受限制,可大大提高计算效率,并为轴心轨迹的自动识别提供了较为精确的依据。
[1] 张丹,侯力,曾颖锋,等. 基于小波消噪的主轴回转精度动态测量法[J].组合机床与自动化加工技术,2015(5):73-79.
[2] 陆峰,沈鸿波,张晓飞,等.基于垂直两点法的电主轴回转精度分析[J].组合机床与自动化加工技术,2014(11):14-18.
[3] 籍永建,王红军,孟哲,等.基于小波去噪算法的主轴轴心轨迹提纯研究[J]. 制造业自动化,2014,36(9):44-45,58.
[4] 张文斌,周晓军,杨先勇,等.基于谐波窗方法的转子轴心轨迹提纯[J]. 振动与冲击,2009,28(8):74-82.
[5] 尹爱军,孙丽萍,王见. 偏微分方程在轴心轨迹提纯中的应用[J].重庆大学学报, 2011,34(12):72-77.
[6] 吴宏钢,尹爱军,秦树人. 基于PDE的振动信号去噪研究[J]. 机械工程学报,2009,45(5):91-94.
[7] Shu Li Mei. HPM-based Dynamic Wavelet Transform and Its Application in Image Denoising[J].Mathematical Problems in Engineering,2013,2013:1-14.
[8] Hua Hong Yan. Adaptive wavelet precise integration method for nonlinear Black-Scholes model based on variational iteration method[J]. Abstract and Applied Analysis,2013,2013:1-6.
[9] L Liu.Construction of interval Shannon wavelet and its application in solving nonlinear Black-Scholes equation[J]. Mathematical Problems in Engineering,2014,2014:1-9.
(编辑李秀敏)
Wavelet Precise Integration Method for Purification to Locus of Journal Center
CAO Yong-ning1,YANG Yong2
(1. Department of Industrial Engineering,Ningxia Vocational and Technical College,Yinchuan 750021,China; 2.Raisecom Technology Co.,Ltd, Beijing 100085,China)
Locus of journal center is often employed to analyze the failure of rotor.In fact, there are much more noises exist in the original signal of the locus of journal center, which is against of the precise analysis to the failure to some extent. The partial differential equation method is a new kind of purification technique for the locus of journal center proposed in recent years. Based on this new method, the wavelet precise integration algorithm is proposed in this paper. As a matter of fact, the wavelet precise integration method (WPIM) is an efficient algorithm to solve the partial differential equation for the purification to the locus of journal center. The numerical experiments show that the proposed method can eliminate the noises in the original signal effectively, and it won’t change the essential feature of the original signal, this is helpful to improve the correctness of the analysis to the locus of journal center.
locus of journal center; purification; wavelet precise integration method
1001-2265(2015)11-0016-03DOI:10.13462/j.cnki.mmtamt.2015.11.005
2015-07-20;
2015-08-15
国家自然科学基金(41171337)
曹永宁(1965—),男,宁夏人,宁夏职业技术学院副教授,硕士,研究方向为现代设计方法及理论,(E-mail)1286319247@qq.com。
TH166;TG506
A
