基于模糊时间窗的再制造装配车间物料配送研究*

张铭鑫，陈鸿海

(合肥工业大学 机械与汽车工程学院,合肥　230009)



基于模糊时间窗的再制造装配车间物料配送研究*

张铭鑫，陈鸿海

(合肥工业大学 机械与汽车工程学院,合肥230009)

针对再制造装配工位物料需求种类、时间的不确定性问题，提出基于模糊时间窗的再制造装配车间物料配送路径优化方法。在对再制造装配车间物料配送特点研究的基础上，综合考虑再制造仓库物料种类分类(再制造件库、再利用件库和新品库)和后续装配成本的需求，在满足生产线平衡条件下，以工位满意度为约束条件，以最小配送成本为目标，建立带模糊时间窗的物料配送路径优化模型，并通过云遗传算法对模型进行求解，利用云模型云滴的随机性和稳定性的优点，设计动态的交叉和变异概率，提高算法的搜索效率。最后，通过实例验证了模型和算法的有效性。

再制造；物料配送；云遗传算法；模糊时间窗

0　引言

再制造是将可利用废旧品经过分类拆解、清洗检查、修复加工、重新装配和调整检测等工序，恢复到“新品”状态的过程[1]。与传统制造的过程相比，再制造过程存在着大量的不确定性因素[2]，主要表现为回收件数量、质量和时间的不确定性。再制造装配过程中使用的零部件不仅包括新品零部件、还有再利用件和再制造件，因此再制造车间中的物料仓库也统分为三类：新品库、再利用件库和再制造件库。新品库中的物料是由外部采购来补充，因此可以随时供需车间物料需求；再利用件库中物料是由废旧件经过拆卸直接回收利用，因此其局限于一定的数量；再制造件库中的物料是由废旧品经过不同的修复工序后到达“新品”质量要求时，补充进来的，因此由于受到再制造件的修复率和修复时间的波动影响，再制造件库的物料量呈随机分布的状态。再制造库存零部件种类和数量的不确定性导致再制造车间物料配送问题比起一般的物流车辆路径规划问题(Vehicle Routing Problem,VRP)更复杂。VRP是近几十年来运筹规划领域研究热点之一。目前，有关VRP问题的研究，已有大量文献。蒋丽等[3]提出一种以工位为中心的生产物流配送思想，建立车间配送优化调度模型，并用遗传算法求解该模型。李晋航等[4]在考虑作业车间内工位物料需求信息、运输时间和时间窗信息不确定性基础上，建立了模糊信息条件下以最小化运输距离为目标的机会约束物料配送车辆规划模型并采用改进的混合智能算法求解。Muller等[5]应用遗传模拟退火算法和两阶段启发式算法相结合，求解带时间窗的车辆调度问题，并取得了一定效果。Repoussis P.P.等[6]利用混合智能算法求解开放式物料配送路径问题，并结合实例验证了模型和算法的可行性。Thibaut Vidal等[7]针对多属性车辆路径问题，提出一个基于组件的启发式框架。Martin Reed等[8]针对多级车辆路径问题，提出一种蚁群扩展算法，通过k-means聚类预处理大大减少了计算时间，提高算法求解效率。

综上所述，目前的VRP问题研究文献主要面向于传统制造车间的物流路径优化问题。再制造装配车间由于物料到达的类型和时间的不确定性所引起的装配方案是不同的。再制造车间的物料配送问题，不仅要考虑车辆路径优化问题，同时还要兼顾由于物料种类不同而引起的后续装配工位的物料成本问题。

本文在借鉴相关文献研究成果的基础上，结合再制造装配车间物料配送的情况，提出基于模糊时间窗的再制造车间物料配送方法，以工位满意度来表征工位物料类型所引起的物料成本的变化，在考虑后续装配成本的前提下，优化物料配送方案。

1　再制造装配车间物料配送模型构建

1.1模糊时间窗

由于再制造装配过程中，新品件、再利用件和再制造件在误差、成本、质量和数量等方面的差异，导致装配方案呈现多样化特点。装配工位的零部件种类的不确定性导致工位的物料需求时间也在一定范围内波动。对于再制造车间而言，相对来说，新品件的采购成本大，再制造件修复成本次之，再利用件拆卸成本最小，因此，为了降低产品最终成本，装配车间希望在满足交货期的前提下，尽量使用再利用件和再制造件，最后考虑新品件。按照生产计划节拍，物料在时间窗[ta,tb]内到达，优先配送再利用件或再制造件，尽量避免配送新品件。因此，本文采用模糊时间窗来描述物料到达的时间的不确定性，利用模糊时间窗的隶属度函数来表征不同的物料类型在时间窗[ta,tb]内到达时对后续装配成本的影响。

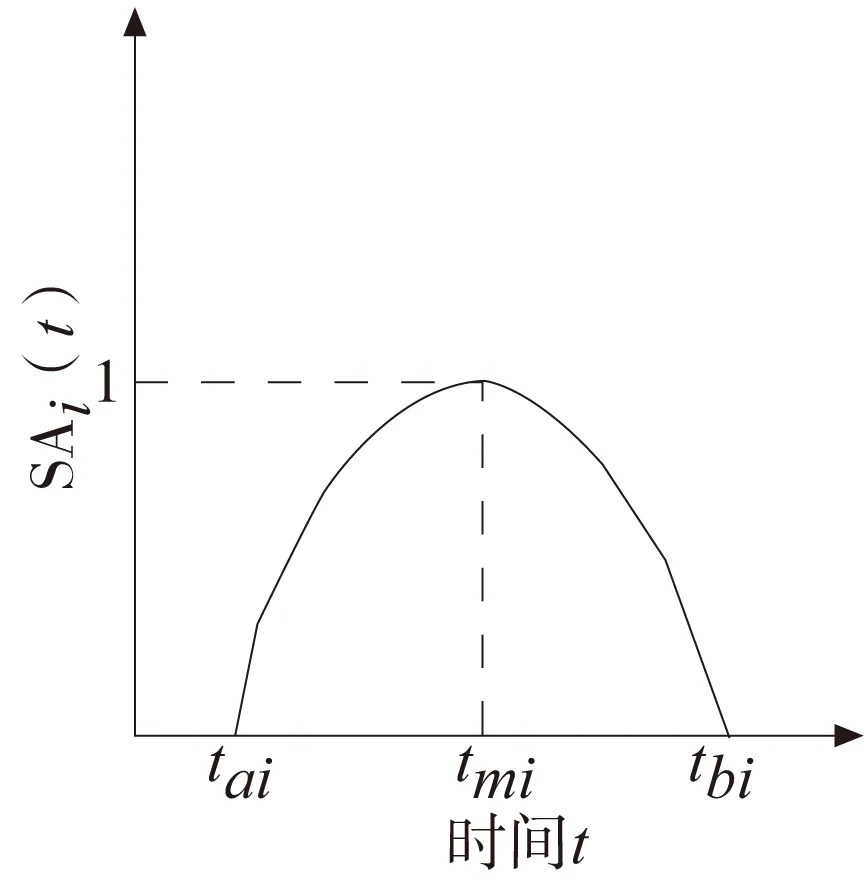
图1　模糊时间窗

模糊时间窗[9]是一种反映顾客偏好的时间窗，可以表示为时间t的凸函数，如图1所示。ta和tb分别表示工位i对所需物料到达时间的最早限制和最晚限制，tm表示物料在该时间点到达时，工位满意度为1。离该时间点越远，工位的满意度就越低。为了保证生产计划的正常执行，物料到达时间落在[ta,tb]之外，工位满意度为0。同时为了区分不同的物料类型到达时，对工位满意度的影响，本文采用幂函数来表征隶属度函数，如式(1)所示。

(1)

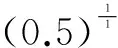
1.2模型构建

(1)问题描述

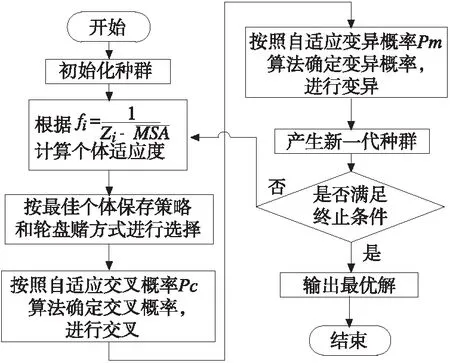
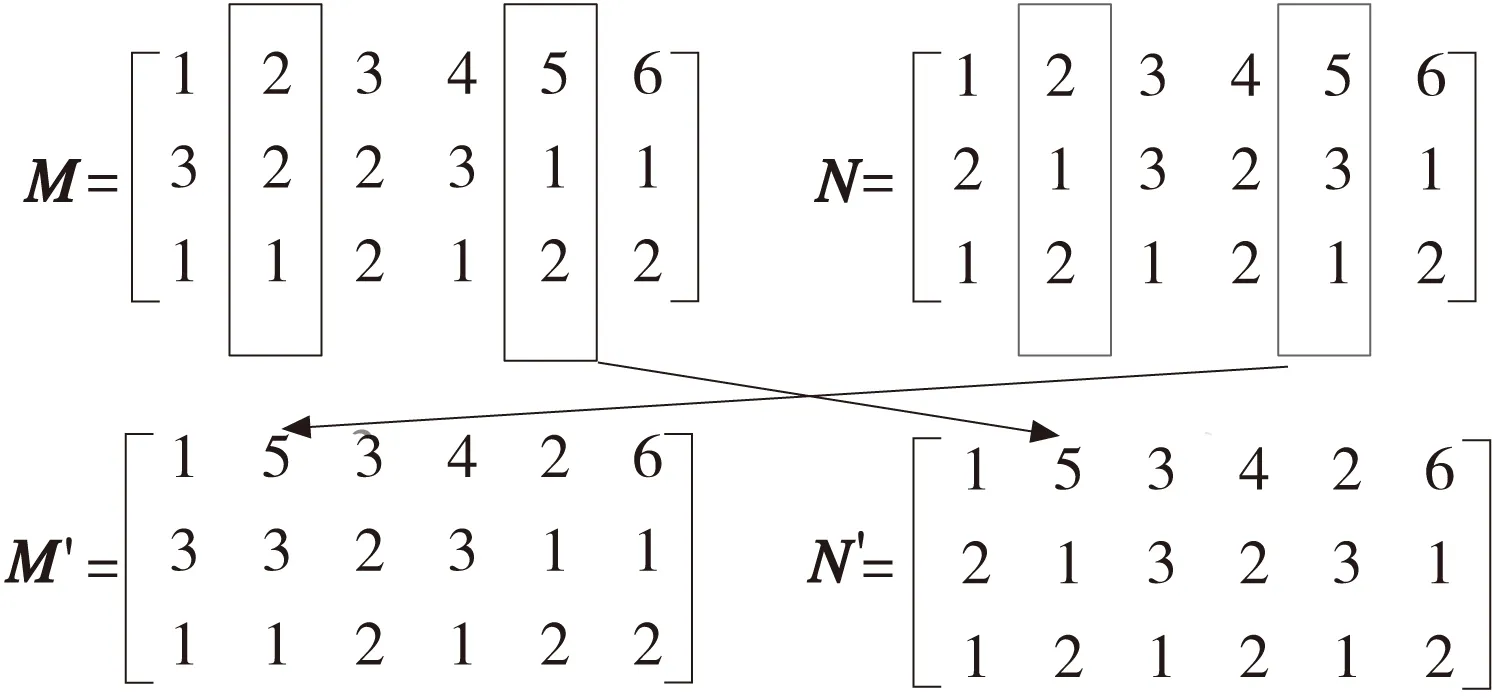
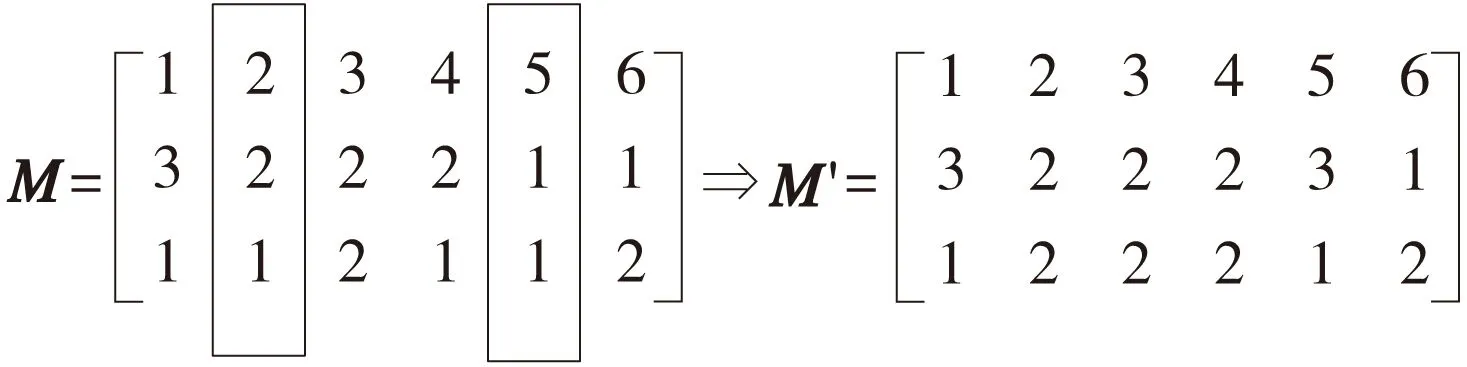
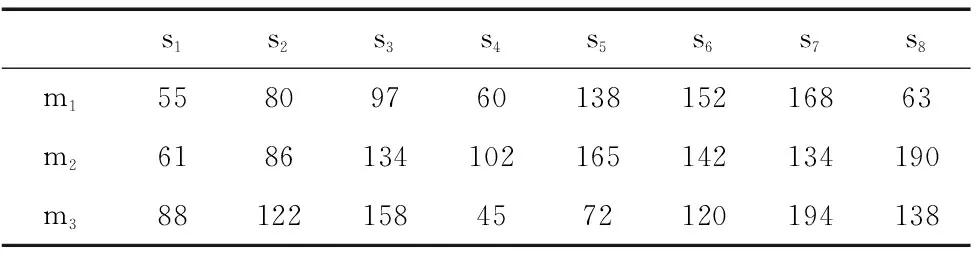
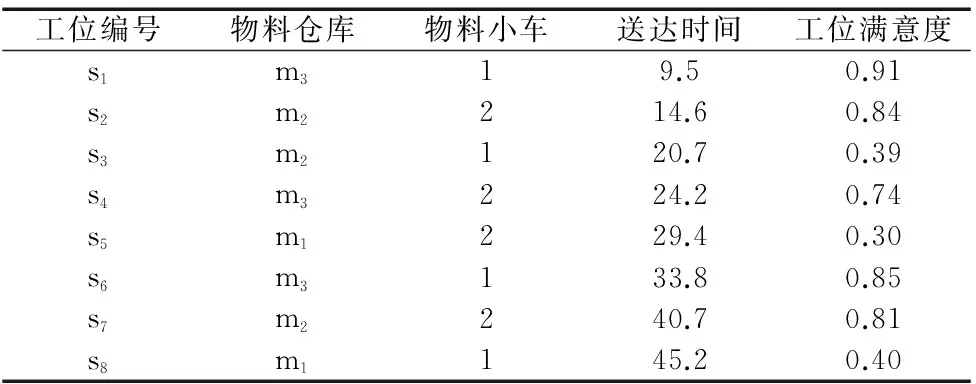
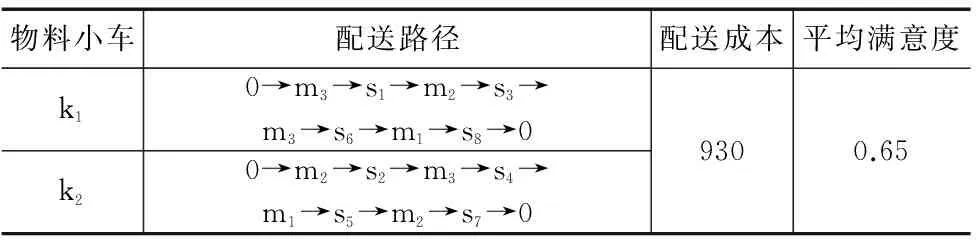
再制造装配车间物料配送车辆路径优化问题一般描述为：一个物料仓库有M个物料库位(其中再制造件有m1个库位，再利用件有m2个库位，新品件有m3个库位，M=m1+m2+m3)，拥有K辆物料小车(一次配送容量为q)，负责对装配线N个工位进行物料配送，工位i的物料需求量为gi(gi

(2)假设条件

①配送开始时，物料小车从物料仓库出发(其初始位置为0)，到达指定配送工位，再返回物料仓库，一个配送循环结束。

②每个工位只能由一辆物料小车配送物料。

③工位所需物料和不能超过物料仓库的总的存储量。

④物料小车不能超过其最大行驶距离。

⑤忽略物料小车初始出发时间。

(3)变量

M：物料配送中心M=1+2+…+m，N：装配线工位集合N=1+2+…+n，K：物料小车集合K=1+2+…+k，cij：物料库位j到工位i的满载运输成本，c’ij：工位i到物料库位j的空载运输成本，dij：工位i到物料库位j的距离，ti：物料小车k到达工位i的时间，α：表示车间工位满意度的最小值。

xik=1表示工位i由物料小车k配送，否则xik=0；

yij=1表示工位i的物料由物料库位j供应，否则yij=0；

xijk=1表示物料小车k由第i个工位回到物料仓库，再由物料仓库到第j个工位配送，否则xijk=0；

(4)配送模型

(2)

模型中，式(2)是以配送成本最小为目标函数；式(3)保证工位配送时间不超过模糊时间窗；式(4)保证每个工位所需物料一次只能由一个物料库位配送；式(5)保证每个工位一次只能由一辆配送小车配送；式(6)和(7)保证每个工位都被服务到，且保证一个工位只能由一个物料库位为其服务；式(8)保证工位满意度大于设定值。

2　模型求解

再制造车间物料配送问题是一种复杂的组合优化问题。遗传算法是求解组合优化问题的一类高效并行全局搜索算法。

2.1云遗传算法

传统的遗传算法采用固定的概率进行交叉和变异操作，存在着早熟收敛和易于陷入局部最优的缺点，影响算法的求解效率。因此，在遗传算法进化搜索过程中动态调整交叉和变异概率成为遗传算法进化的方向。在遗传算法中引入云模型理论[10]，利用云模型云滴的随机性和稳定性的优点，由云模型的X条件云发生器来控制遗传算法进化搜索过程中的交叉和变异概率的自适应过程，在确保最大适应度周围的优秀个体维持正态云模型稳定倾向性的同时，提高适应度较低个体的搜索能力，提高了算法在搜索精度和范围上的准确性。交叉概率Pc和变异概率Pm的自适应公式以及云遗传算法流程图如下所示。

(1)自适应交叉概率Pc的算法：

He= En/C2

(2)自适应变异概率Pm的算法：

Ex= f

He= En/C4

(3)云遗传算法流程图如图2所示。

图2　云遗传算法流程图

2.2编码

一般的VRP问题都采用一维自然数编码方式。由于再制造车间物料配送问题涉及车辆分配和工位用料方案的选择，因此本文采用二维自然数编码方式。例如6个工位，3类物料仓库和2辆物料小车的配送方案矩阵M表示：

式中：x为工位编号，y为物料仓库编号，z为车辆编号。工位1、2采用再利用件库3的物料，工位3、4、5采用再制造件库2的物料，工位6采用新品件库的物料；物料小车1负责工位1、2、5的物料配送，物料小车2负责工位3、4、6的物料配送。

2.3适应度函数

适应度函数是算法中评价个体优劣的函数，用于指导算法中进化的搜索方向，适应度值高的个体优先遗传到下一代种群中。对于某配送矩阵，在满足约束条件的基础上，除了其配送成本越小越好以外，还希望其工位满意度越大越好。因此其适应度函数由目标函数和工位.满意度函数转化而成fi：

2.4选择操作

本文采用保留最佳个体和轮盘赌相结合的方式生成下一代种群。将上一代种群中的个体按适应度值从大到小排列，选择最优的父代个体，直接进入下一代种群；剩下的个体采用轮盘赌的方式生成。该方法既能避免有效基因的损失，又能使高适应度值的个体以更大的概括生存，从而提高算法的全局收敛性和计算效率。

2.5交叉操作

对于选择操作得到的种群，由云模型X条件发生器算法根据适应度来生成概率Pc，随机选取两个父代对应基因段位置进行交叉操作。

2.6变异操作

为了维持种群的多样性，由云模型X条件发生器算法根据适应度生成概率Pm，进行变异操作。随机选取两个父代基因段，保持工位编号顺序不变的情况下，对配送中心编号和车辆编号进行变异，产生新的配送方案。

3　实例验证

以某再制造主减速器主锥总成装配线为例，该装配线共有8个工位、3类物料仓库(m1为新品库、m2为再制造件库、m3为再利用件库)、由两台物料小车负责配送物料，物料仓库到各工位的距离如表1所示，为简化计算，本文通过距离来表征运输成本，物料小车的满载成本是运输距离的1.5倍，空载成本是运输距离的1.0倍，车间要求工位满意度α≥0.6，各工位模糊时间窗如表2所示。

表1　物料仓库到各工位的距离

表2　各工位的模糊时间窗

本实例是在MatlabR2009上实现云遗传算法，设种群规模为50，最大迭代次数为50，C1=C3=3.0，C2=C4=10，k1=k3=1.0，k2=k4=0.5，计算结果如表3所示，最优配送路径如表4所示。

由表3和表4可知，两辆物料小车经过45.2min完成了一次物料配送，在满足车间工位满意度的前提下(0.65>0.6)，最小的配送成本为1930单位，装配工位优先采用再利用件库和再制造件库的物料，为了不影响生产节拍，s5和s8工位采用再新品件库物料。

表3　计算结果

表4　最优配送路径

4　结论

针对再制造车间物料配送的复杂性，通过模糊时间窗来表征再制造车间物料需求的波动性，通过工位满意度来表征物料类型对后续装配成本的影响，在此基础上，构建了再制造装配车间的物料配送模型。针对遗传算法存在的缺点，利用云模型云滴的随机性和稳定性特点，在遗传算法中应用云模型理论进行交叉和变异的自适应优化，提高了算法的求解效率，为再制造装配车间物料配送问题的研究开拓了思路。

[1]LundRT.Remanufacturing[J].TechnologyReview,1984,87(2):18-23.

[2]GuideVDR,WassenhoveLNV.Managingproductreturnsforremanufacturing[J].ProductionandOperationsManagement,2001,10(2):142-155.

[3] 蒋丽,丁斌,藏晓宁.以工位为中心的生产物流配送优化[J].计算机集成制造系统,2009,15(11):2153-2159.

[4] 李晋航,黄刚,贾艳.多模糊信息条件下的物料配送路径规划问题研究[J].机械工程学报, 2011, 47(1): 124-131.

[5]MullerJApproximativesolutionstothebicriterionVechicleRoutingProblemwithTimeWindows[J].EuropeanJournalofOperationalResearch,2010,202(141):223-231.

[6]RepooussisPP，TarantilisCD，BraysyO.Ahybridevolutionstrategyfortheopenvehicleroutingproblem[J].Computers&OperationsResearch,2010,37(3):443-455.

[7]ThibautVidal,TeodorGabrielCrainic,MichelGendreau,etal.Aunifiedsolutionframeworkformulti-attributevehicleroutingproblems[J]EuropeanJournalofOperationalResearch,2014,234(3):658-673.

[8]MartinReed,AlikiYiannakou,RoxanneEvering.Anantcolonyalgorithmforthemulti-compartmentvehicleroutingproblem[J].AppliedSoftComputing, 2014,15: 169-176.

[9]ChengR,GenM.Fuzzyvehicleroutingandschedulingproblemusinggeneticalgorithms[J].GeneticAlgorithmsandSoftComputing, 1996,683-709.

[10] 王伟鑫,王旭,葛显龙.任务可拆分的多模式多项目调度模型与算法[J].计算机集成制造系统, 2014,20(6): 1388-1397.

(编辑李秀敏)

Research on Material Distribution of Remanufacturing Assembly Workshop Base on Fuzzy Time Windows

ZHANG Ming-xin，CHEN Hong-hai

(School of Mechanical and Automotive Engineering, Hefei University of Technology, Hefei 230009,China)

Aiming at the uncertainty of the material demand and processing time, the optimization method based on the fuzzy time window for the material distribution in the re-assembly shop. Analyzing the attributes of the material distribution in the re-assembly shop, the categories of the materials (re-manufactured parts, re-used parts, new parts) and the cost of the succeeding assembly are both considered. Under the balance condition of the production line, using the satisfaction degree as the constraint and the minimizing the distribution cost as the target, an optimization model based on the fuzzy time window for the material distribution is established. The cloud genetic algorithm is adapted for solving this model. Due to the randomness and stability of the cloud droplet, design the dynamic crossover and mutation probability to improve the searching efficiency. Finally, a study case is taken to verify the feasibility and effectiveness of the model.

remanufacturing；material distribution；cloud genetic algorithm；fuzzy time windows

1001-2265(2015)11-0133-04DOI:10.13462/j.cnki.mmtamt.2015.11.037

2015-01-27

国家重点基础研究发展计划资助项目(973计划，2011CB013406)

张铭鑫(1980—)，男，河北张家口人，合肥工业大学讲师，博士研究生，研究方向为生产系统建模与仿真，(E-mail)zhmxcatchpp@163.com。

TH186;TG506

A