微型电动车车架静态及预应力模态分析研究

路春光，郭灿志，刘宝刚，邓程程

（1.华北理工大学 机械工程学院，唐山 063009；2.上汽唐山客车有限公司，唐山 063299）

0 引言

车架是汽车的装配基体和承载基体，支撑连接汽车的各总成零部件，承受来自车内外的各种载荷，其好坏直接关系到整车的性能和质量[1]。因此，车架必须具有足够的强度与刚度，同时也应有合理的动态特性以降低整车的振动保证车体结构良好的可靠性、耐久性。针对前述问题，特别对电动游览车在实际行驶中可能遇到的典型工况进行了分析，此过程中对于网格质量的好坏对分析结果的影响程度也做了理论的计算，得到了可以接受的分析结果，对电动汽车车架的设计和优化提供了重要的参考依据。如图1所示为所研究纯电动旅游观光车实物图。

图1 非公路用旅游观光车实物图

1 车架有限元模型的建立

1.1 三维实体模型

应用ANSYS/Workbench进行有限元分析时，虽然Workbench带有自建模功能模块Design Modeler，但是为了提高工作效率，本文采用成熟的三维建模软件Creo进行车架实体模型的建立， 然后利用Workbench软件成熟的双向CAD接口，把三维车架数字模型导入Workbench软件。

车架是一个复杂的装配体，主要由槽钢和角钢通过焊接连接而成。建模时，为保证网格质量及有限元模型能够在ANSYS软件中高效率的计算及计算的准确性，在不影响车架结构主要力学特性的前提下，尽量简化其几何模型特征。故对车架作了简化处理，具体措施如下[2]。

1）由于车架是各槽钢、角钢焊接连接而成，在建立有限元模型时将车架处理为一个刚体，全部简化成实体单元，从而即简化有限元计算又保证了载荷的传递。

2）略去功能件和装饰件。 有些构件仅为满足工艺或美观要求而设置的，并非根据强度要求设置的，原则上是可以忽略的。如：工艺孔、前端横梁两端的圆弧修饰等。

3）删除一些对结构分析只产生局部较小影响的细节， 如车架横纵梁上的部分圆角、倒角过度和局部空洞，删除这些较小的细节可以大大减小有限元分析的计算量和求解时间，而不会影响到分析结果精度。车架三维模型及承受载荷的位置如图2所示。

图2 车架三维模型及承受载荷位置图

其中载荷1处放置了电机、控制器各一台；载荷2处主要承载驾驶和副驾驶两人；载荷3处驾驶座下放置两块铅酸蓄；载荷4处底架放置三块铅酸蓄电池；载荷5处背靠背两排座椅供乘坐六人。电动汽车车架上各主要总成质量及载荷大小如表1所示。

表1 各部件质量参数

其中，重力加速度g取10N/kg。

1.2 材料的选择

车架采用的所有槽钢、角钢均使用普通碳素结构钢Q235，材料特性如表2所示。

表2 车架材料特性

1.3 单元选择及网格划分

由于车架结构较为简单，并没有过多的曲面存在，所以在此选用 SOLID185 实体单元采用Workbench直接进行网格划分。为了得到网格划分质量的好坏对分析结果影响程度的可靠数据，在满载弯曲工况下先后进行了二次网格划分计算，分别采用自由网格划分和单元大小为10mm、边缘长度为1.8mm的四面体单元网格划分，单元和节点数分别为29085、56792和353361、698611。两次网格划分的网格质量统计如图3、图4所示。

图3 自由划分时的网格质量分布图

图4 约束单元大小时的网格质量分布图

由此可见，第一次的划分的网格质量是非常坏的，而第二次的网格划分的柱状图统计表重心分布在0.75左右，说明绝大多数网格质量是好的。尽管有一部分不好的网格，但考虑到计算机的硬件性能问题后认为这样的网格质量是可以接受的。Workbench中坐标设定及车架有限元模型局部图如图5所示。坐标设定具体如下：车架高度方向为X方向，正方向为由下指向上方；长度方向为Y方向，正方向为由车架前方指向车架后方；车架的宽度方向为Z方向，正方向为面对车架尾部由左指向右。

图5 单元为10mm的有限元模型局部图

2 工况的选择

电动车运行时车架承受的载荷很复杂，就载荷性质而言，主要为弯曲、扭转、侧向载荷和纵向载荷等几类。本文结合非公路用旅游观光车的特点，既观光车为景区内用车，通常情况下为满载运行并且车速也不太高，而景区路面条件较好，所以车架受力主要按照非公路用旅游观光车最常见的两种工况来进行分析计算，分别为满载弯曲和紧急制动[3,4]。

满载弯曲工况模拟电动汽车满载静止状态或在平坦路面匀速直线行驶时产生的对称垂直载荷[5]。此工况下车底架扭曲变形小，主要受轮胎与地面接触处产生的支反力作用，车底架主要承受弯曲载荷，产生较小的水平弯曲变形。

紧急制动工况为垂直载荷和纵向载荷共同作用的相对复杂工况，纵向载荷是由电动车在制动时的惯性力的作用而产生的。紧急制动工况主要考察当电动车以极限制动加速度0.8g （此工况车辆最大减速度约为0.7g）制动时，惯性力对车架的影响。

3 静态特性分析

3.1 满载弯曲工况

1）载荷处理：根据力的等效原则，将电动机、控制器、电池、驾乘人员等各部分重量转化为等效载荷施加在车架的相应位置上；车架自重采取质量和重力加速度的方式施加[6,7]。

2）边界条件处理：在充分考虑电动汽车在满载弯曲工况下运行的状态后，在车架前桥左右两端均施加全自由度约束，在后桥左右两端施加X方向的约束，其他方向及旋转自由度不做约束。

3）计算结果及分析：此工况下对两次不同的网格划分情况进行有限元模拟，分别得到了两种情况下电动汽车车架结构在满载弯曲工况下的等效位移和应力分布情况。其分析结果数据对比如表3所示。

表3 分析结果数据对比表

由以上的计算结果对比情况说明，在进行有限元计算时划分网格质量的好坏对计算结果的可信度影响非常大。在此例中的误差均在50%以上，就此可以认为在网格质量比较糟糕的情况分析计算的结果是不可信。所以在进行有限元分析时，一定要保证网格质量在可接受的范围内。以后的分析中将不再对这种坏质量网格的划分情况进行分析。

在网格大小为10mm时，车架的位移变形云图和等效应力云图分别如图6、图7所示。该工况下应力最大值为140.5MPa，发生在前桥悬架弹簧支点处，车身材料均为屈服极限为235MPa的普通碳素结构钢Q235。 该工况考虑安全系数为2.0[8]。但是车架实际安全系数为1.68。由此可见车架此部分在满载弯曲工况下不满足强度要求。所以，应该此处应该使用更高强度的材料，如屈服极限为345MPa的碳素结构钢Q345等材料。

图6 位移变形云图

图7 等效应力云图

车架最大变形为1.6989mm，发生在载荷3、载荷5位置处。

3.2 紧急制动工况

1）载荷处理：除弯曲工况施加的载荷和车身自重外，还需在与行驶方向的反向即在Y的正方向施加一个0.8g的极限制动加速度。

2）边界条件处理：在此工况下，在车架前桥左右两端均施加X、Y、Z方向的位移约束，在后桥左右两端处施加X、Z方向的约束，其他方向及旋转自由度不做约束。

3）计算结果及分析：该工况下应力最大值为324.48MPa，发生在前桥悬架弹簧支点处，车身材料均为屈服极限为235MPa的普通碳素结构钢Q235。该工况考虑安全系数为1.5[8]。说明车架实际处于不安全的状态下。由此可见车架此部分在紧急制动工况下不满足强度要求。因此，必须在此处使用更高强度的材料，如屈服极限为345MPa的碳素结构钢Q345等材料。计算时施加的加速度为极限制动加速度0.8g，但是在车辆实际行驶过程中绝对不会达到这样的极限值，所以当所换用材料的安全系数大于1时，就可以满足车辆安全行驶的要求。车架紧急制动工况下位移变形云图和等效应力云图分别如图8、图9所示。

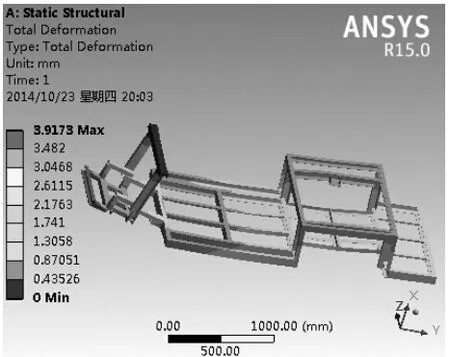
图8 位移变形云图

图9 等效应力云图

车架最大变形为3.9173mm，发生在车架前端前防撞梁处。

4 预应力模态分析

模态分析是动态分析的基础，是计算结构振动特性的数值技术，可以帮助设计人员确定结构的固有频率和振型，从而使结构设计避免共振，并指导工程师预测在不同的载荷作用下结构的振动形式。因为结构中的应力会导致结构的刚度发生变化，这方面典型的例子就是琴弦，张紧的琴弦比松弛的琴弦声音尖锐，这是因为张紧的琴弦刚度更大，从而导致自振频率更高的缘故[9]。

根据模态分析理论，一般只计算结构的前几阶固有频率和振型，因为越低阶振动对结构影响越大。结合车架的载荷情况及运行工况，计算分析车架结构的前10阶模态[10～12]。对于车架来说，弯曲及扭转振动是其结构动态特性的主要表现形式。但是，对于非公路用旅游光车弯曲振动对车架强度的影响最大，因为景区用观光车行驶时路面条件好，常常只受到对称垂直载荷的作用，这类载荷是最易激发车架结构的弯曲模态。

基于以上分析，运用大型有限元分析软件Workbench对车架进行了预应力模态分析，获取了弯曲模态下的前10阶固有频率值及其振型特征如表4所示。

如图10～图13所示，给出了车架结构前4阶固有频率与振型图（放大数倍）。

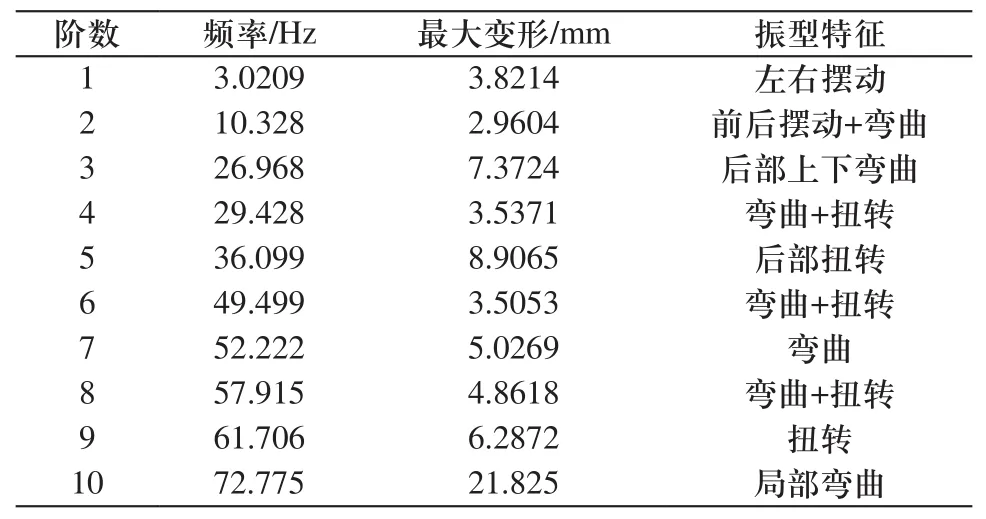
表4 前10阶固有频率值及其振型特征

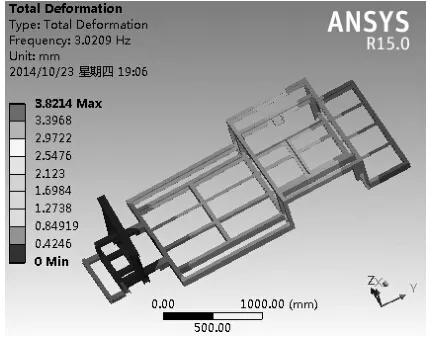
图10 一阶振型

图11 二阶振型

图12 三阶振型

图13 四阶振型

当车架某阶固有频率与外界激励频率相接近时，就会产生共振现象，为避免共振对车架带来的危害，应使固有频率远离外界的激励频率。对于电动汽车来说路面的激振频率一般在20Hz以内，良好的路面激振频率仅5Hz左右。除此之外也应使车架不与非簧载质量的固有频率重合，其固有频率一般为6Hz～15Hz[13]。

由预应力模态分析可知，对于此电动车来说只有一阶固有频率位于路面的激励频率内，说明车架在良好的路面行驶时车架振动变形较小，有良好的动态特性。但二阶频率处在非簧载质量的固有频率以及普通路面激励频率范围内，这就可能会产生难以预期的振动，所以应给予关注。

5 结束语

通过对电动观光车车架结构的动静态分析，得到了车架结构各位置的应力状态和振动特性， 确定了车架结构的薄弱环节。从静力学分析结果来看，车架在满载弯曲工况下车架前桥悬架横梁实际安全系数为1.68，这在遇到极端情况时可能会处于危险状态；在极限紧急制动工况下，前桥悬架横梁不满足安全条件，必须更改此处的设计方案。从动力学分析结果来看，前2阶的固有频率容易引起共振，应通过调整车架结构，使各阶模态频率不处在路面激励频率和非簧载质量的固有频率范围内，防止车体发生共振，增加整车的安全性和乘坐人员的舒适性。

[1] Beermann.H.J.Statie ana1ysis of eommereia1 vehie1e frames：ahybrid fi nite elementanaly tieal.International Journal of Vehiele Design,1984(5):26-52.

[2] 张建,戚永爱,唐文献,等.基于有限元法的某卡车车架优化设计[J].机械设计与制造,2012(5).

[3] 沈永峰,郑松林,冯金芝.公路客车车架与车身骨架强度及模态分析[J].现代制造工程,2013(7).

[4] 吕东升,王东方,苏小平.基于HyperWorks的某客车车架有限元分析[J].机械设计与制造,2011(3).

[5] 李辉.客车车身骨架有限元分析与轻量化改进设[D].合肥:合肥工业大学,2006.

[6] 邵超城,刘强,龙飞永.纯电动汽车车架设计及有限元分析[J].机械设计与制造,2011(8).

[7] 王军,马若丁,王继新,等.矿用自卸车车架强度有限元分析[J].工程机械,2008(11):29-32.

[8] 李良巧.机械可靠性设计与分析[M].北京:国防工业出版社,1998.

[9] 丁欣硕,凌桂龙.ANSYS Workbench14.5从入门到精通.北京:清华大学出版社,2014.

[10] 熊永华,杜发荣,高峰,等.轻型载货汽车车架动态特性分析与研究[J].机械设计,2007,24(4):60-62.

[11] 李延斌,张潮,姜彤,等.轮式装载机前车架的模态分析[J].机械设计与制造,2013(9):110-112.

[12] 杨忠炯,赵晓海,王宇奇.重型矿用汽车车架模态分析及改进[J].机械传动,2009(3):97-99.

[13] 褚玉锋,王铁,刘伦伦,等.TY型工程自卸车车架动态特性的设计分析[J].机械设计与制造,2014(3).